Понятие функции. Область определения и множество значений функции

1. Понятие функции. Область определения и множество значений функции

2. Введение

Функция - одно из важнейших понятий математики, она даёт возможность
исследовать и моделировать не только состояния, но и процессы. Исследование
процессов и явлений с помощью функций — один из основных методов
современной науки. Вы будете изучать функции во всех последующих классах и в
высших учебных заведениях.
• Мы часто сталкиваемся с ситуациями, когда значение одной переменной
зависит от значения другой. Рассмотрим примеры подобных ситуаций.
• При пешей прогулке пройденное расстояние зависит от времени прогулки.
• Площадь квадрата зависит от длины его стороны.
• Урожайность помидоров в теплице зависит от количества воды, которой их
поливали во время роста.
• В каждом из этих примеров есть независимая переменная, которая может
менять своё значение (время прогулки, длина стороны, количество воды),
и зависимая от неё переменная (пройденное расстояние, площадь,
урожайность).

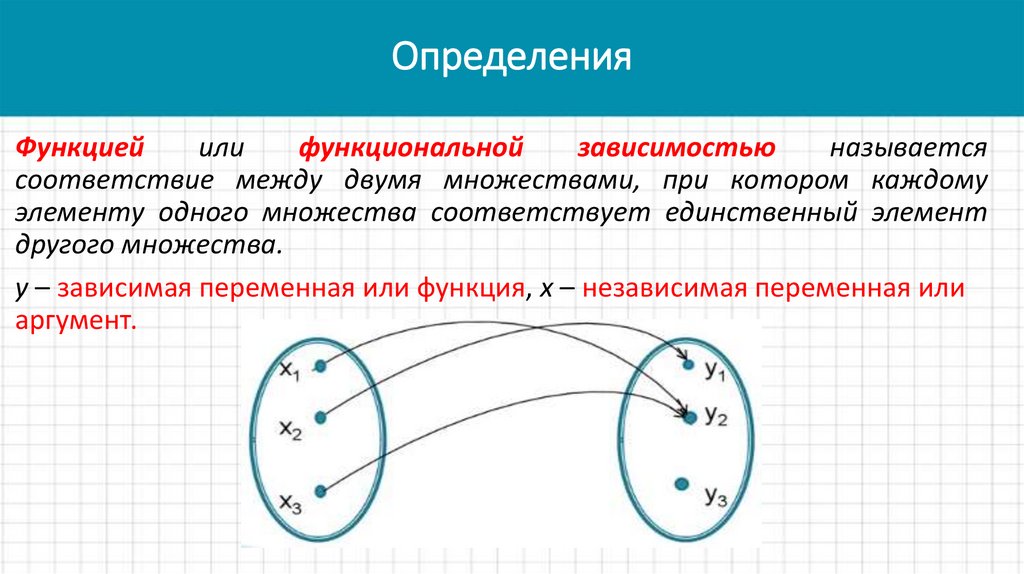
3. Определения

Функцией
или
функциональной
зависимостью
называется
соответствие между двумя множествами, при котором каждому
элементу одного множества соответствует единственный элемент
другого множества.
y – зависимая переменная или функция, x – независимая переменная или
аргумент.

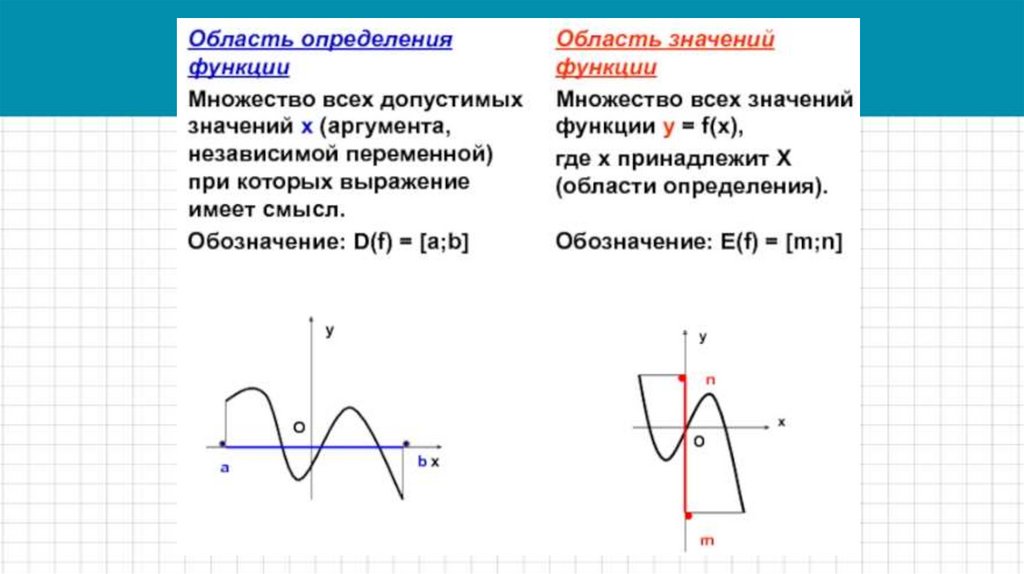
4. Обозначения

5.

6.

7. Способы задания функции

Задать функцию значит определить правило, в соответствии с которым по
значениям независимой переменной можно найти соответствующие ее
значения.
Табличный способ — помогает
быстро определить конкретные
значения без дополнительных
измерений или вычислений.
Графический способ — самый
наглядный. На графике сразу
видно возрастание и убывание
функции, наибольшие и
наименьшие значения, точки
максимума и минимума.
Словесный способ.
Аналитический способ — через
формулы. Компактно, и можно
посчитать функцию при
произвольном значении
аргумента из области
определения.

8. Пример 1

5
Найдите значение функции y(x) = 3x + 5 при x = 0; x = 5; x = -3; x = 1,4; x = .
6
Решение
y(0) = 3 0 + 5 = 5
y(5) = 3 5 + 5 = 20
y(-3) = 3 (-3) + 5 = -4
y(1,4) = 3 1,4 + 5 = 9,2
5
5
y( ) = 3 + 5 = 7,5
6
6
5
Ответ: y(0) = 5, y(5) = 20, y(-3) = -4, y(1,4) = 9,2, y( ) = 7,5
6

9. Пример 2

Найдите значение аргумента при котором значение функции
y(x) = 7 - 2x равно 1.
Решение
7 - 2x = 1,
- 2х = 1 – 7,
-2х = -6,
х = -6:(-2)
х=3
Ответ: y(x) = 1 при х = 3

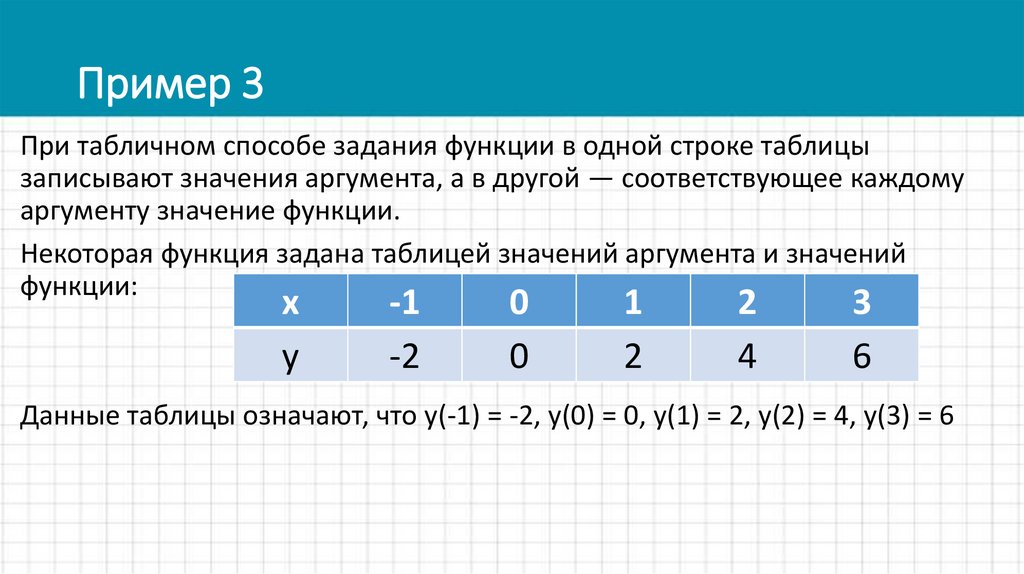
10. Пример 3

При табличном способе задания функции в одной строке таблицы
записывают значения аргумента, а в другой — соответствующее каждому
аргументу значение функции.
Некоторая функция задана таблицей значений аргумента и значений
функции:
x
y
-1
-2
0
0
1
2
2
4
3
6
Данные таблицы означают, что у(-1) = -2, у(0) = 0, у(1) = 2, у(2) = 4, у(3) = 6

11. Пример 4

С помощью графиков можно описать
функции,
которые
сложно
задать
формулой. Например, функцию значения
температуры воздуха в зависимости от
времени суток, график этой функции
(зависимости) представлен на рисунке.
При помощи графика ответьте на
вопросы:
1) Какая температура была в 6 часов, в 12
часов, в 22 часа?
2) В какое время температура воздуха
равнялась -1 С, 3 С, 4 С, 0 С?

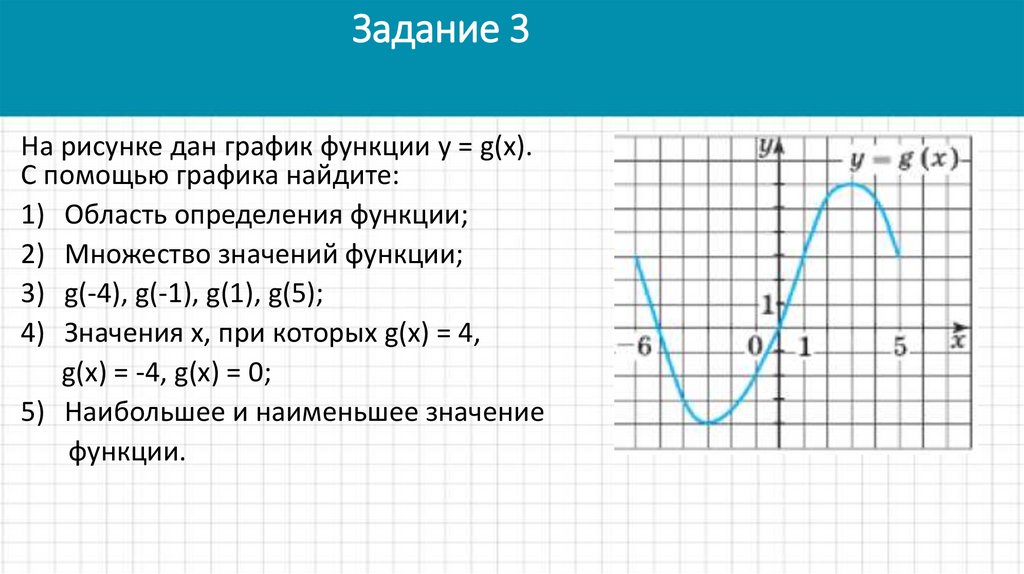
12. Пример 5

13. Проверь себя!

Каждому натуральному числу m ставится в соответствие
остаток x от деления этого числа на 6. Найдите x, если m =
19

14. Проверь себя!

Каждому
натуральному
числу m ставится в соответствие
остаток x от деления этого числа на
6. Найдите x, если m = 53.
Ответ: 5

15. Проверь себя!

Каждому
натуральному
числу m ставится в соответствие
остаток x от деления этого числа на
6. Найдите x, если m = 34
Ответ: 4

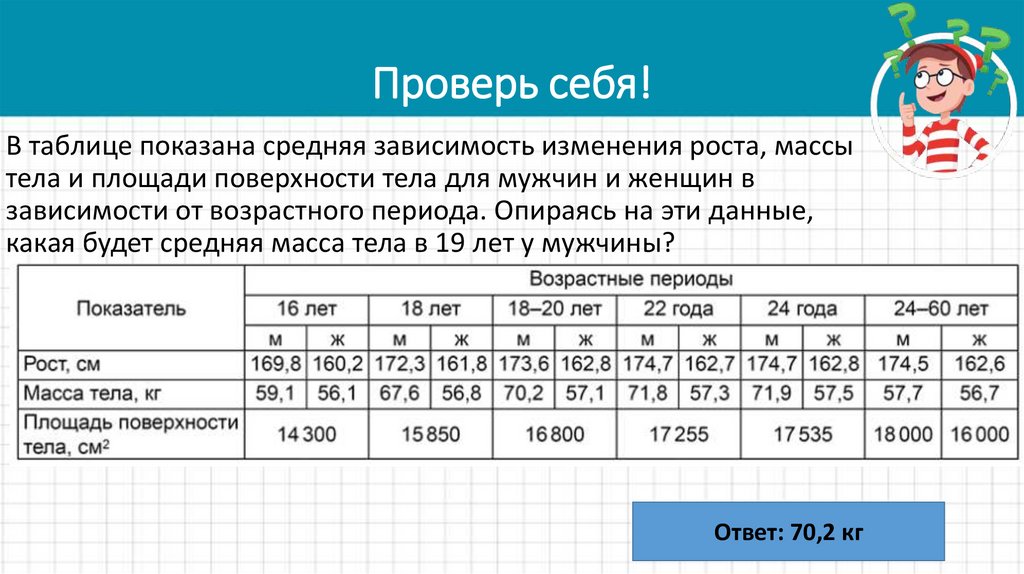
16. Проверь себя!

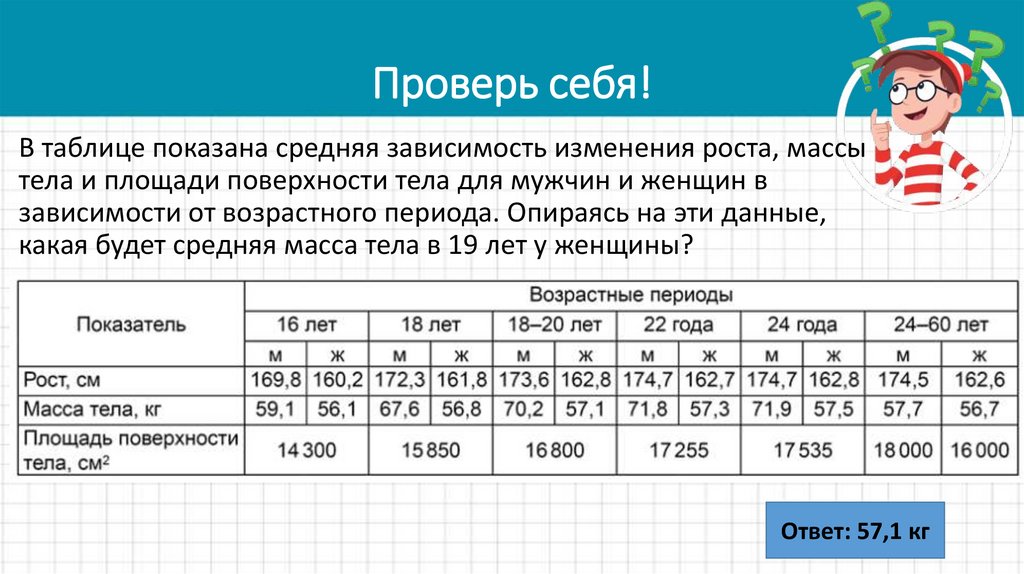
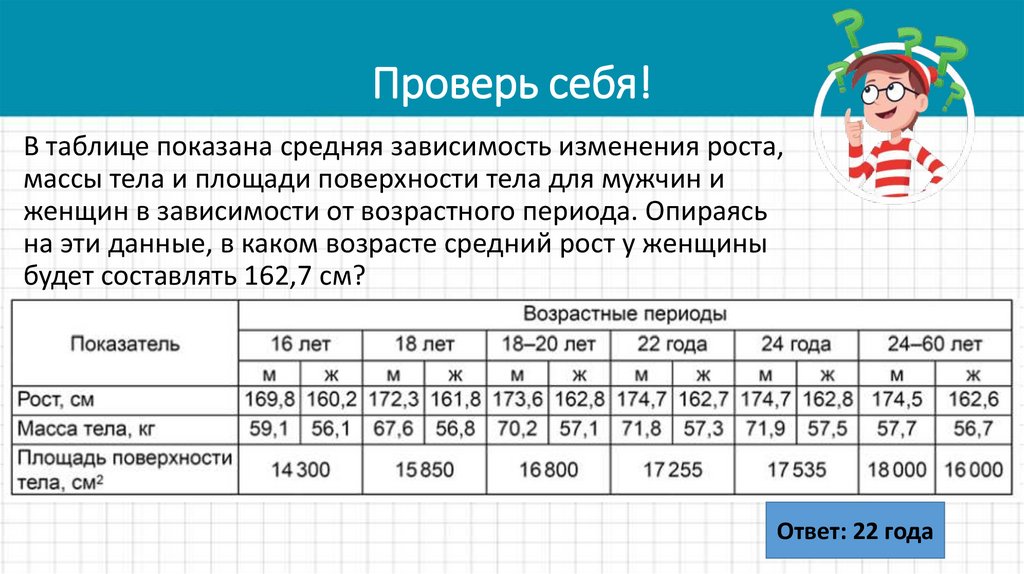
В таблице показана средняя зависимость изменения роста, массы
тела и площади поверхности тела для мужчин и женщин в
зависимости от возрастного периода. Опираясь на эти данные,
какая будет средняя масса тела в 19 лет у мужчины?
Ответ: 70,2 кг

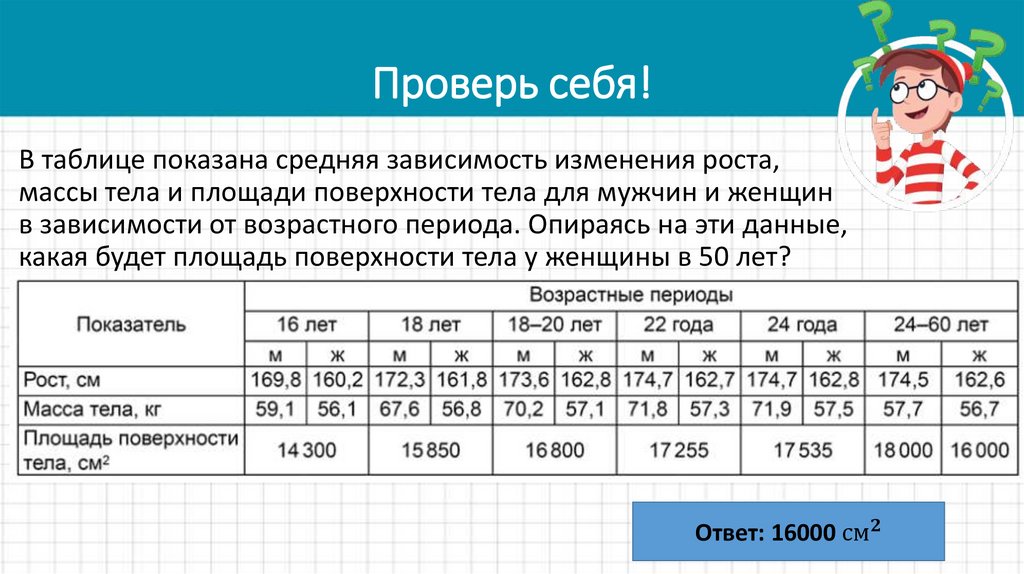
17. Проверь себя!

В таблице показана средняя зависимость изменения роста,
массы тела и площади поверхности тела для мужчин и женщин
в зависимости от возрастного периода. Опираясь на эти данные,
какая будет площадь поверхности тела у женщины в 50 лет?
Ответ: 16000 см