Similar presentations:
Область определения и область значений функции
1. Область определения и область значений функции
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ
Математика есть такая наука,
которая показывает, как из
знаемых количеств находить
другие, нам еще неизвестные.
Д.С. Аничков
2.
Цель урока: научиться находить область определенияфункции, заданной формулой.
Задачи урока:
Повторить понятие функции, области определения и
области значений функции;
Повторить нахождение области определения и
области значений функции, заданной графиком;
Систематизировать знания по нахождению области
определения и области значений функций,
изученных ранее.
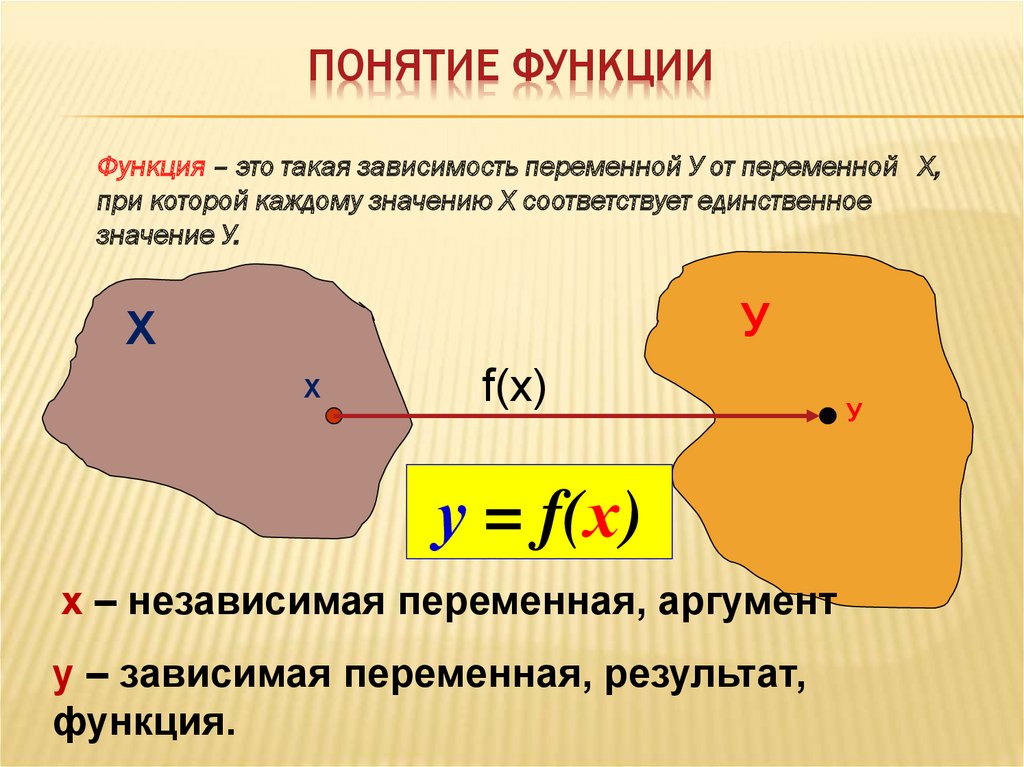
3. Понятие функции
ПОНЯТИЕ ФУНКЦИИФункция – это такая зависимость переменной У от переменной Х,
при которой каждому значению Х соответствует единственное
значение У.
У
Х
Х
f(x)
у = f(х)
х – независимая переменная, аргумент
у – зависимая переменная, результат,
функция.
У
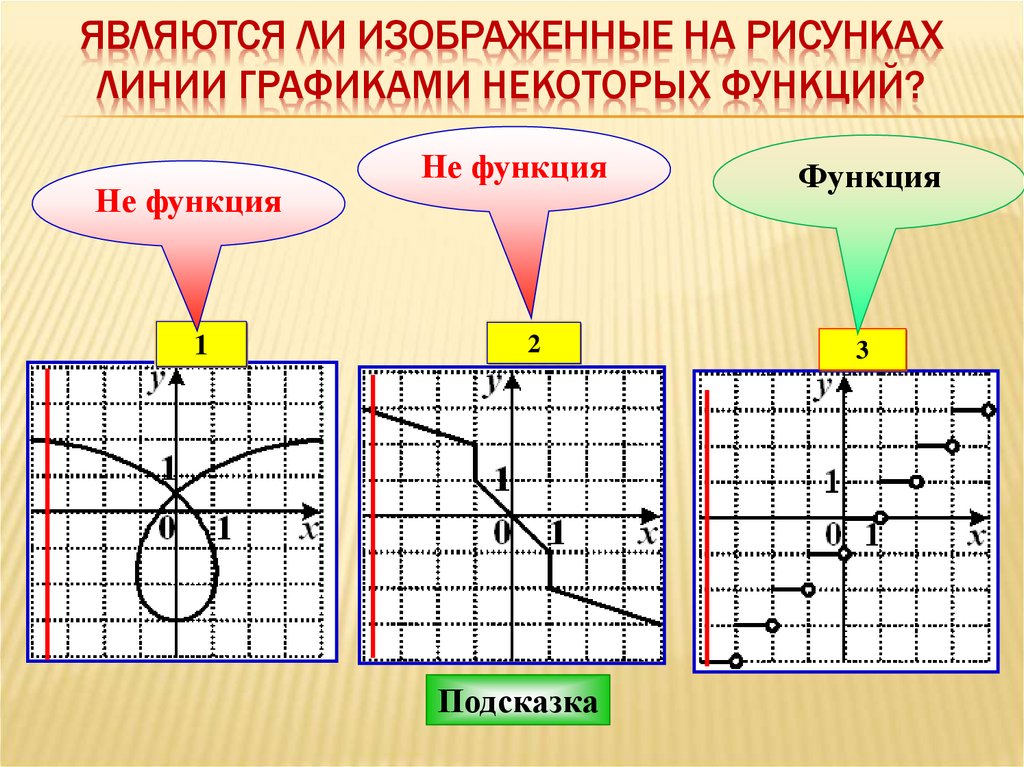
4. Являются ли изображенные на рисунках линии графиками некоторых функций?
ЯВЛЯЮТСЯ ЛИ ИЗОБРАЖЕННЫЕ НА РИСУНКАХЛИНИИ ГРАФИКАМИ НЕКОТОРЫХ ФУНКЦИЙ?
Не функция
1
Не функция
2
Подсказка
Функция
3
5. Являются ли изображенные на рисунках линии графиками некоторых функций?
ЯВЛЯЮТСЯ ЛИ ИЗОБРАЖЕННЫЕ НА РИСУНКАХЛИНИИ ГРАФИКАМИ НЕКОТОРЫХ ФУНКЦИЙ?
Рис.1
Рис.2
у
0
х
у
0
х
6. Область определения и область значений функции
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ
Все значения независимой переменной х образуют
область определения функции D(f)
Все значения, которые принимает зависимая переменная у,
образуют область значений функции E(f)
Область значений
функции
E(f)
(х)
у
f
Область определения
функции
х
D(f)
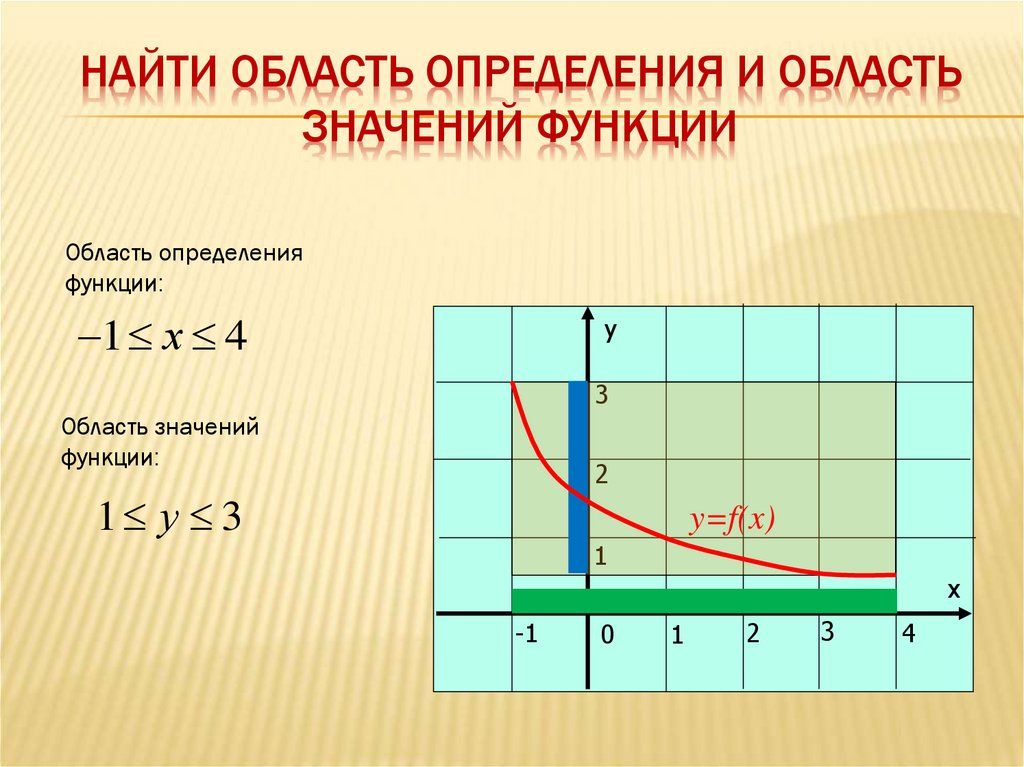
7. Найти Область определения и область значений функции
НАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ
Область определения
функции:
1 х 4
у
3
Область значений
функции:
2
1 у 3
y=f(x)
1
х
-1
0
1
2
3
4
8.
у1
у = f(x)
х
0 1
Ответ:
Какова
функции?
Каковаобласть
областьопределения
значений функции?
E(f)
D(f)==[-2;4]
[-5;5]
9.
уу = f(x)
1
-1
0
х
0 1
Вопрос:
Какова
Каковаобласть
областьзначений
определения
функции?
функции?
Ответ:
; 1
;1;1
1;
10. найти область определения и область значений функции по ее графику
НАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ ПО ЕЕ ГРАФИКУ
D( у) 0;2 2;
у
Е( у) ; 1 0;
0
-1
2
х
11. Область определения и область значений функции
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ
№ Аналитическая
модель
1
у кх в
График
функции
у
у
3
к
х
у ах вх с
а 0
2
Область значений
D( y ) ( ; ) Е ( y ) ( ; )
0
2
Область определения
х
у
к 0
0
х
у
к 0
а 0
ув
0
а 0
х
ув
D( y) ( ;0) (0; ) Е ( y) ( ;0) (0; )
D( y ) ( ; )
Е ( y) ув ;
Е ( y) ; ув
12. Область определения и область значений функции
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬЗНАЧЕНИЙ ФУНКЦИИ
№ Аналитическая
модель
График
функции
4
у
у х
0
5
у
х
Область значений
D( y ) ( ; )
Е( y) 0;
х
у
0
Область определения
х
D(y) 0;
Е( y) 0;
13.
1) y 3 х 22) y 3х 2 2
3) y х 12
х 12 0
3х
4) y
х 23
х 23 0
5) y 2 х 2 3х 4
34
6) y
х 45
1
7) y
2х 1
х 2 3х 4 0
х 45 0
2 х 1 0
14. Найдите область определения функции:
НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ:Вариант 1
Вариант 2
y х2 2
6
2) y
x 2
y х 2 31
23
2) y
3 х
1)
3)
y
1)
х 4
3)
2
y
х
4 х 12
4)
6 х 23
5) y
x 2 3х
2
y
х
2 х 43
4)
6х 2
5) y
x2 2х
6)
y
х 4
2
7) y х 2 х 43х
8) y х 2 4 х 3
5
6)
y
х 9
2
y х 4 12 х 2 13х
3
х 5
y 2 х
5
х 2
7)
8) y
х2 9
х 3
х 12
5
х 4
15. Проверь себя
ПРОВЕРЬ СЕБЯВариант 1
1)
2)
D(y) ;
D( у) ; 2 2;
Вариант 2
1)
D(y) ;
2)
D( у) ;3 3;
3)
D(y) 4;
3)
D(y) 2;
4)
D(y) ;
4)
D( y) ;
5)
D( у) ; 3 3;0 0;
6)
D(у) ; 3 3;
5)
6)
D( у) ; 2 2;0 0;
D(у) ; 2 2;
7) D(y)
8)
;
D( y) 2;
7)
D(y) ;
8)
D(у) 4; 3 3;12 12;
16.
Задание на дом№8.6 (а), 8.11 (б), 8.16 (а, б), 8.22
17.
18.
Историческая справкаРене Декарт.
(1596-1650),франц.
философ, математик,
физик, филолог. Заложил
основы аналитической
геометрии, дал понятие
переменной величины и
функции, ввел многие
алгебраические
обозначения.









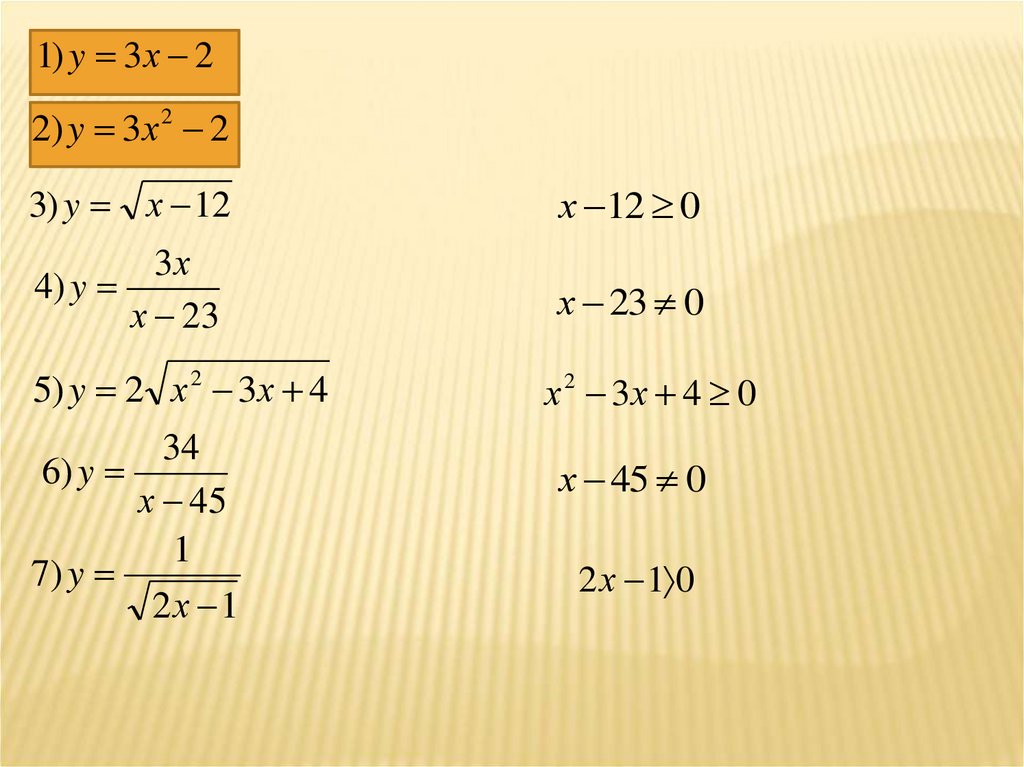





 mathematics
mathematics








