Функция. Область определения функции

1.

2.

Определение
Если каждому значению х из некоторого
числового множества Х поставлено в соответствие
по правилу f определенное число у, то говорят, что
на множестве Х задана функция у=f(х).
у = f(х), х Є Х
х – независимая переменная (аргумент)
у – зависимая переменная (функция)
Х – область определения функции

3.

Функцией
называется
переменной
от
другой,
зависимость
при
котором
одной
каждому
значению независимой переменной соответствует
единственное значение зависимой переменной.
Обозначают: у= f(x)

4.

Областью определения
функции называется
множество всех значений
независимой переменной х,
т.е. аргумента.

5.

ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ
Область определения функции – множество
всех значений, которые может принимать х.
1) знаменатель ≠ 0
2) подкоренное выражение ≥ 0
Например:
у = 5х + 1
х – любое число
х – любое число
х – любое число, кроме 0
х≥0
?

6.

НАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ
D(f): 5х + 12 ≠ 0
5х ≠ −12
х ≠ −12 : 5
х ≠ −2,4
х Є R, х ≠−2,4
х Є(-∞;-2,4)U(-2,4;+∞)

7.

НАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ
D(f): (х − 4)(х+2) ≠ 0
х ≠4
х ≠ −2
х Є R, х ≠ - 2, х ≠ 4
х Є(-∞;-2)U(-2;4)U(4;+∞)

8.

НАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ
D(f): 5х – 13 ≥ 0
5х ≥ 13
х ≥ 13:5
D(f): 17 − 2х > 0
−2х > −17
х < −17 : (−2)
х ≥ 2,6
2,6
[2,6;+∞)
х < 8,5
8,5
(−∞; 8,5)

9.

НАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ
+
0,25 −
+
1
(−∞; 0,25] U [1; +∞)
+
−1 −
+

10. Задание: найти область определения функции по ее графику

1)
2)
3)
4)
Задание: найти область определения
функции по ее графику
D(у) 4; 1 1;
у
D( у) ;0 0;2
D(у) 4; 1 1;
D( у) 4;
-1
0
х

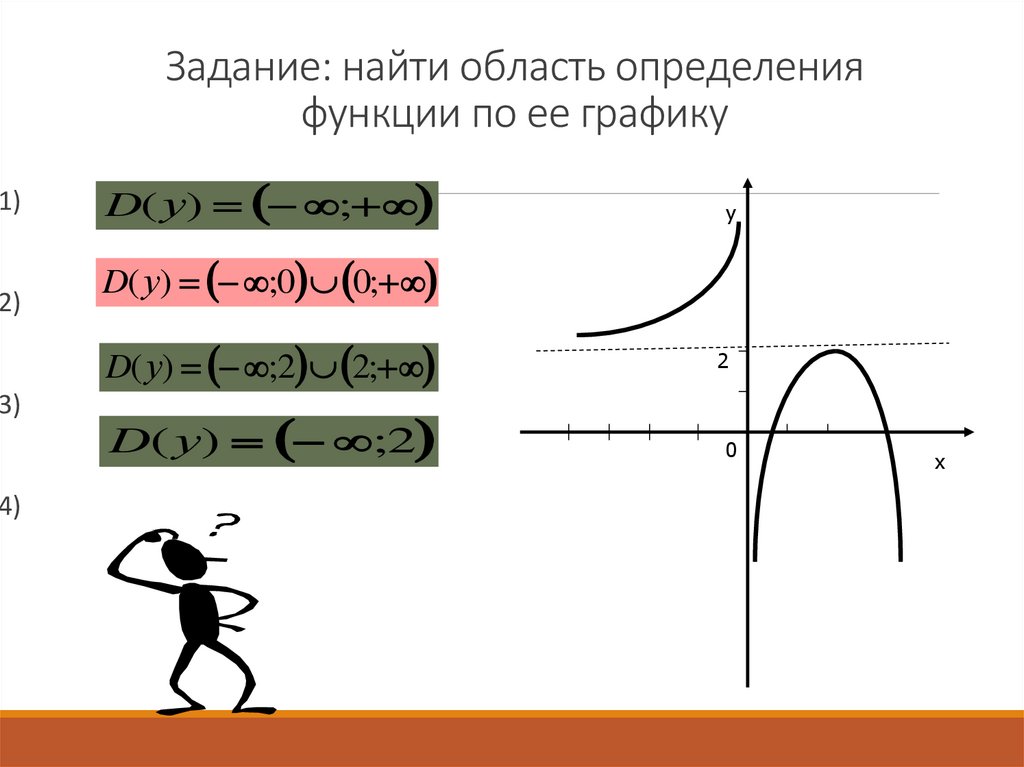
11. Задание: найти область определения функции по ее графику

1)
2)
3)
4)
Задание: найти область определения
функции по ее графику
D( у) ;
у
D(у) ;0 0;
D(у) ;2 2;
D( у) ;2
2
0
х

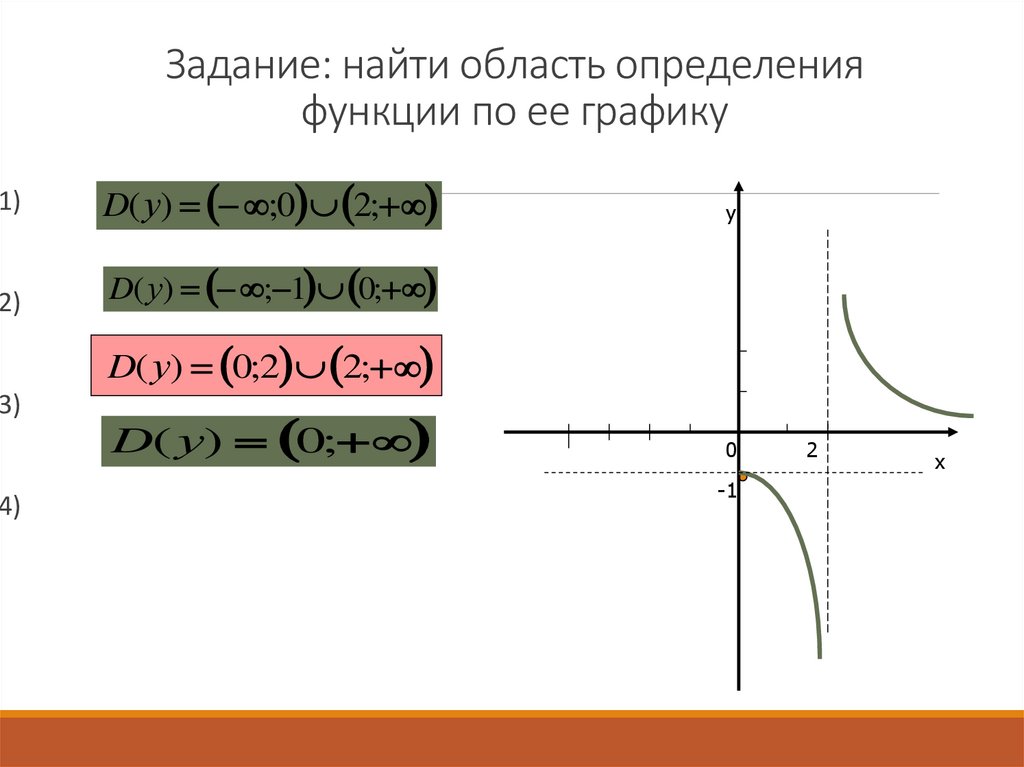
12. Задание: найти область определения функции по ее графику

1)
D(у) ;0 2;
2)
D(у) ; 1 0;
3)
4)
у
D( у) 0;2 2;
D( у) 0;
0
-1
2
х

13. Условия существования функции

№
1
2
3
4
5
Формула
g ( x)
f ( x)
f ( x) 0
y 2n f ( x)
1
y
2n f ( x)
y log a f ( x)
f ( x) 0
y log g ( x) b
g ( x) 0;
g ( x ) 1.
g ( x) 0;
g ( x) 1;
f ( x ) 0.
f ( x) 0 ;
y
6
y log g ( x) f ( x)
7
8
9
y f ( x) p , где p нецелое, p 0
y f ( x) p , где p нецелое, p 0
y tgt
10
y ctgt
условия
f ( x) 0
f ( x) 0
f ( x) 0
n, гдеn Z
2
t n, гдеn Z
t