Similar presentations:
Область определения и область значений функции
1. Область определения и область значений функции
Цели.Изучить понятия:
1) область определения функции
2) область значений функции
Уметь находить область определения функции и область значений
функции.
Уметь находить значение функции при заданном значении аргумента.
Уметь находить значение аргумента при заданном значении функции.
2.
Функцией называют такую зависимость однойпеременной (зависимой) от другой (независимой),
при которой каждому значению независимой
переменной соответствует единственное значение
зависимой переменной .
y f (x)
Независимую переменную (х) называют
аргументом , зависимую переменную называют
функцией от этого аргумента.
3.
Принято независимую переменную(аргумент)
обозначать буквой х, а зависимую переменную –
буквой у, функцию (правило, которое задает
зависимость) – буквой f.
Если у зависит от х, то этот факт можно записать
так: у = f(х)
Читаем: игрек равен эф от х.
Например: у = х + 7 или f(х) = х + 7
4.
Все значения, которые принимает независимаяпеременная, называют областью определения
функции.
Обозначается D(у)
Все значения, которые принимает
зависимая переменная, называют
областью значений функции.
Обозначается Е(у)
5. 1. Найдём по графику область определения функции - D(у)
-54
Т.к. область определения функции – это все значения, которые
принимает независимая переменная, т.е. х, то по графику определим:
какие значения принимает х?. Опустим из крайних точек графика
перпендикуляры на ось абсцисс (ось Ох) и определим значения х.
Это
х = - 5 и х = 4,5 Значит область определения функции х Є [– 5; 4,5]
Записывается это так (см следующий слайд)
6. Найдите по графику область определения функции - D(у)
-5D(у)= [-5; 4,5]
4
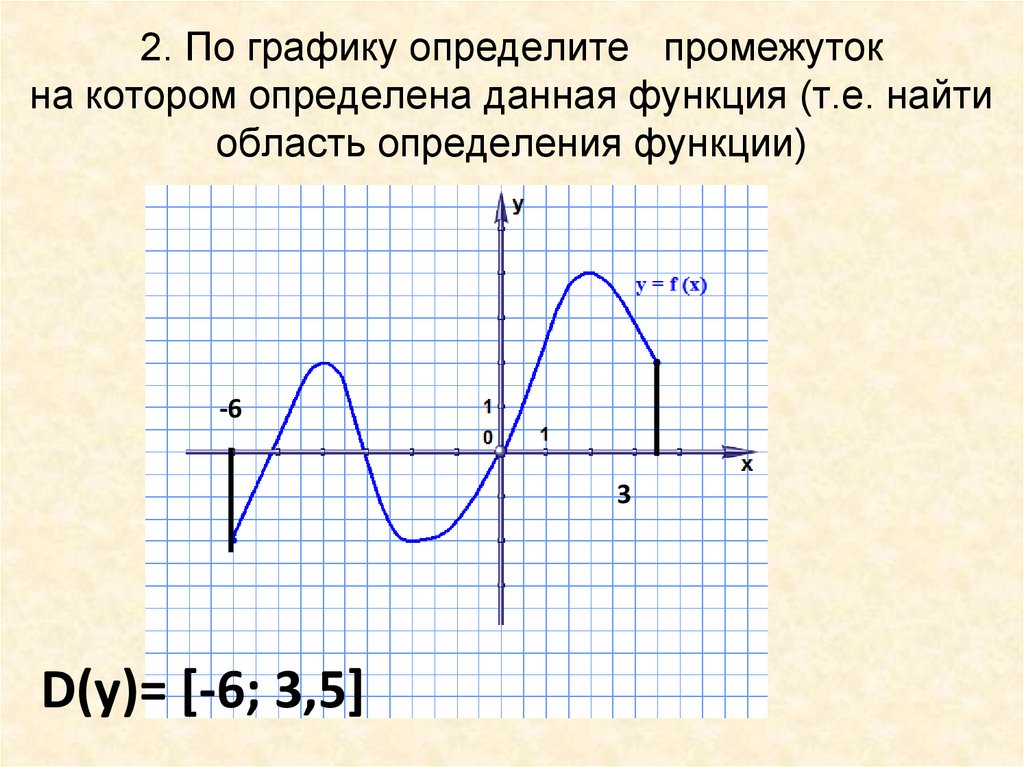
7. 2. По графику определите промежуток на котором определена данная функция (т.е. найти область определения функции)
-63
D(у)= [-6; 3,5]
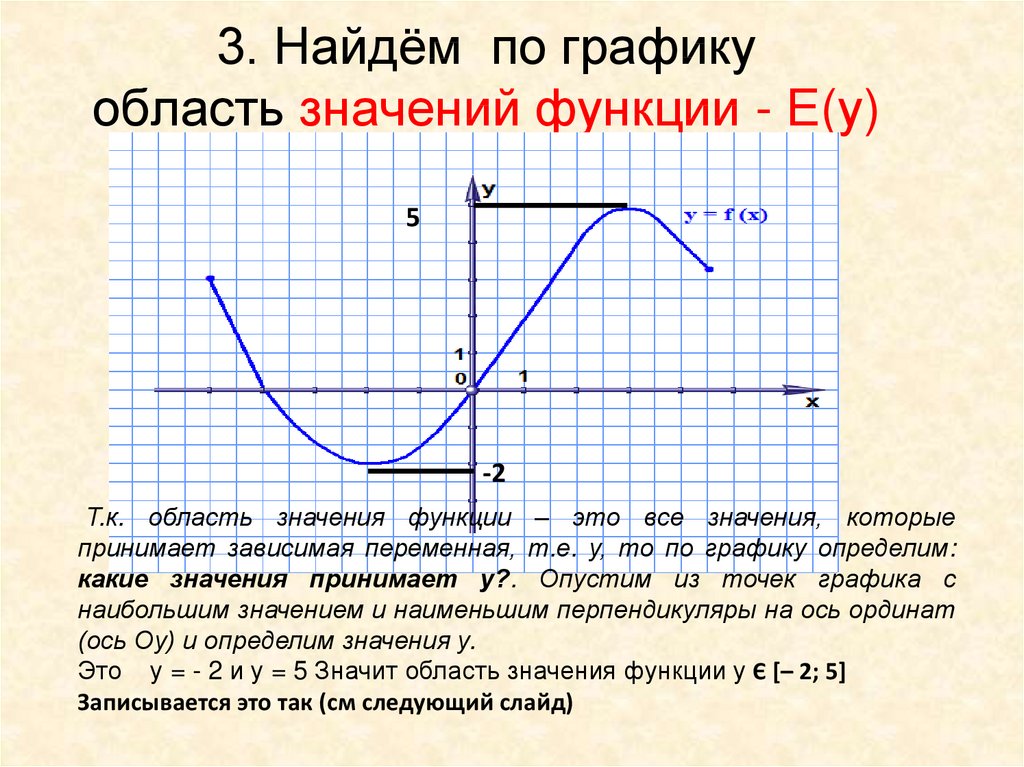
8. 3. Найдём по графику область значений функции - Е(у)
5-2
Т.к. область значения функции – это все значения, которые
принимает зависимая переменная, т.е. у, то по графику определим:
какие значения принимает у?. Опустим из точек графика с
наибольшим значением и наименьшим перпендикуляры на ось ординат
(ось Оу) и определим значения у.
Это у = - 2 и у = 5 Значит область значения функции у Є [– 2; 5]
Записывается это так (см следующий слайд)
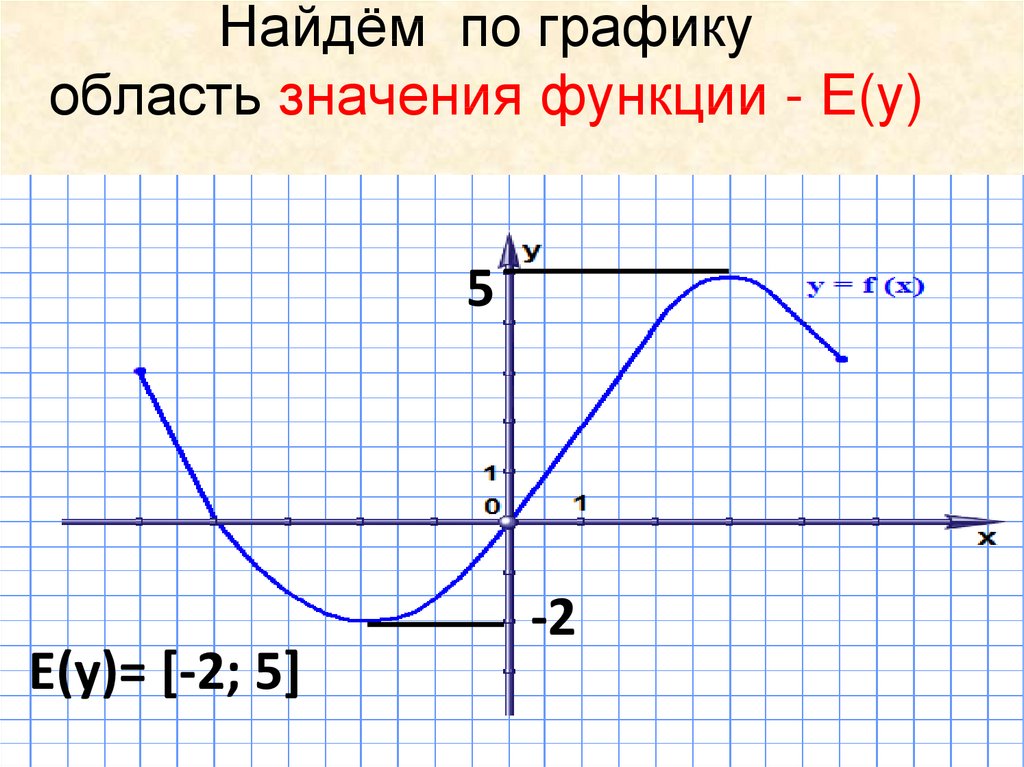
9. Найдём по графику область значения функции - Е(у)
5Е(у)= [-2; 5]
-2
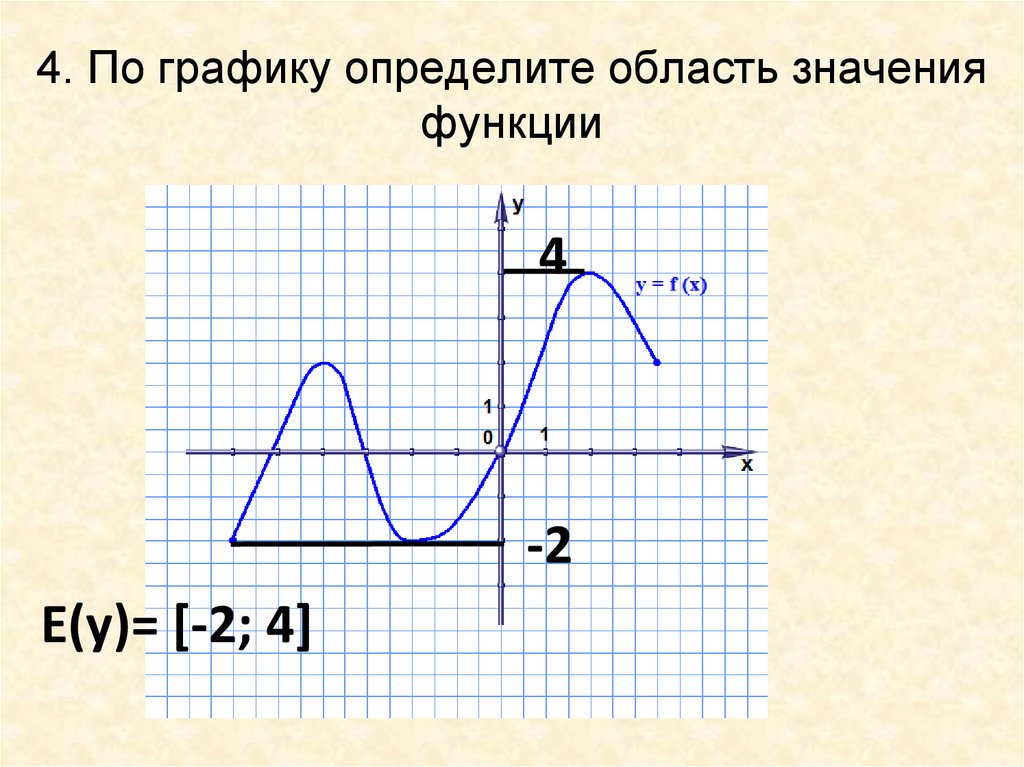
10. 4. По графику определите область значения функции
4-2
Е(у)= [-2; 4]
11. 5. Найдите по графику область определения функции
-55
D(у)= [-5; 5]
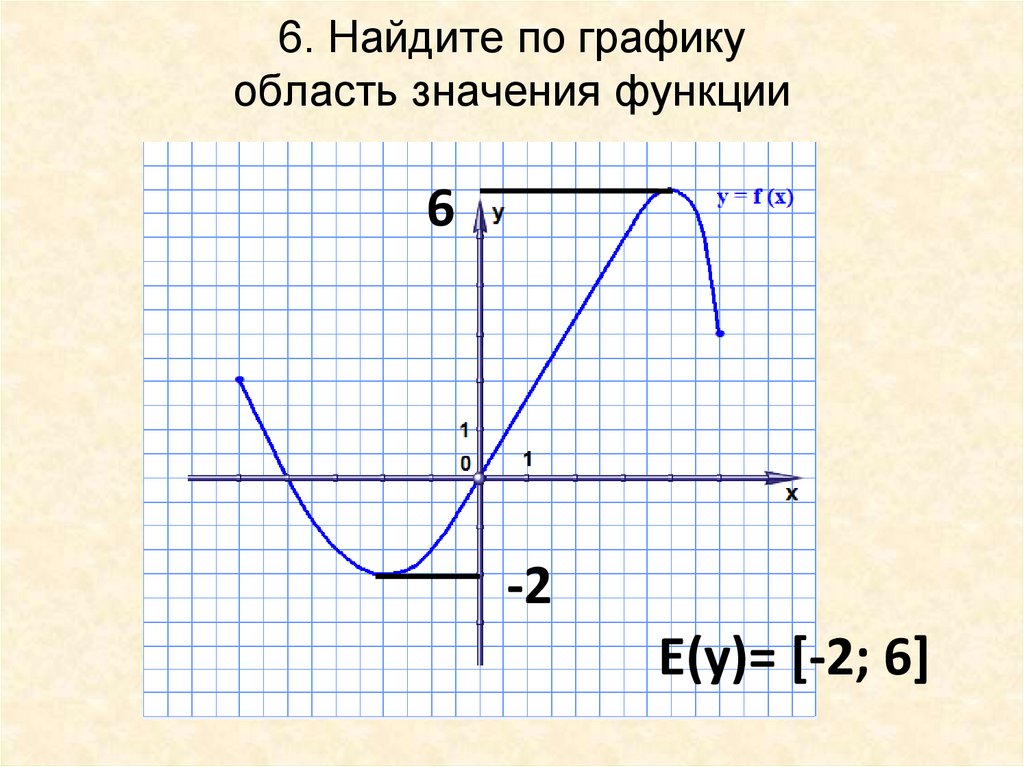
12. 6. Найдите по графику область значения функции
6-2
Е(у)= [-2; 6]
13.
Задание 7. Найдём область определения функции:у х 2 х;
3
Решение
у х 2 х;
3
Рассуждаем: В данном случае
вместо аргумента (х) можно
подставить любое число.
Следовательно область
определения – все числа.
Записываем: D(у) = (-∞; + ∞)
14.
Задание 8. Найдём область определения функции:3
у
х 11
Решение
Рассуждаем: На нуль делить нельзя.
Значит по смыслу знаменатель не
должен быть равен нулю.
Пишем:
х 11 0
х 11
Значит область определения – все
числа, кроме числа 11 .
Ответ: D(у)= (-∞; 11) U (11; + ∞)
.
15. Задание 9. Функция задана формулой у = 3х – 5.
1. Найти значение функции при значении аргумента, равного -2; 0.Образец оформления. (формулу записывать обязательно)
: у = 3х – 5
При х = - 2,
∙
у(-2) = 3 (-2) – 5 = - 6 – 5 = - 11;
Объяснение: в формулу, с помощью которой задана функция,
вместо х подставим его значение и вычислим
при х = 0 у(0) = 3 * 0 – 5 = - 5
2. Найти значение аргумента при значении функции, равном 10.
у(х) = 10, то 3х - 5 = 10
3х = 15
х=5
Объяснение: в формулу, с помощью которой задана функция,
вместо у подставим значение функции. Получим линейное
уравнение которое необходимо решить. Находим значение х
(аргумента).
16.
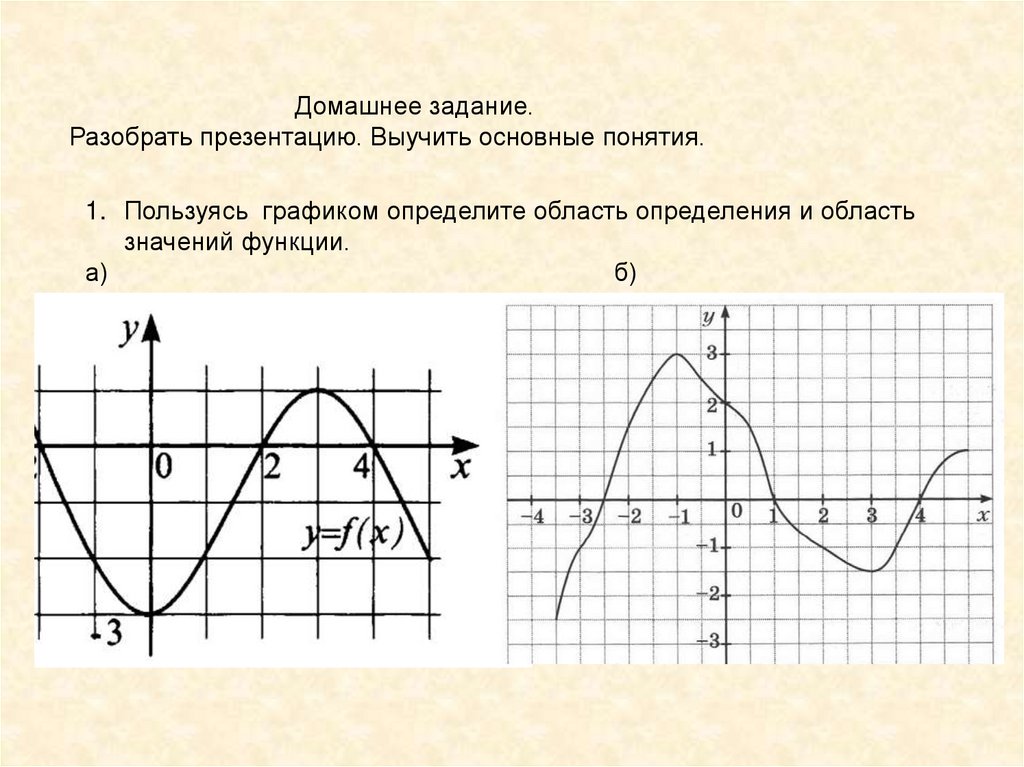
Домашнее задание.Разобрать презентацию. Выучить основные понятия.
1. Пользуясь графиком определите область определения и область
значений функции.
а)
б)
17.
г)у
78
2 х 18
у
х
24 х
13 х
у
2
д)
х 25
№791, 794
Образец решения д)
2х 9
у 2
х 16
Рассуждаем: на нуль делить нельзя. Значит по смыслу
знаменатель не должен быть равен нулю
Пишем:
2
х 16 0
Разложим на множители с помощью формулы разность квадратов
( х 4)( х 4) 0
х 4 0
х 4 0
х 4
х 4
-4
4
Область разбита на три части точками -4 и 4
Ответ: D(у)= (-∞; -4) U (-4;4) U (4; + ∞)











 mathematics
mathematics








