Лінійна алгебра

1.

Підготували
Студенти групи Ф-24:
Дідів Мар’яна;
Дідів Наталя.

2.

1. Визначники другого і третього порядку. Властивості визначників.
2. Матриці та дії з ними. Ранг матриці. Обернена матриця.
3. Системи лінійних рівнянь. Метод Гаусса, Метод Крамера.
Матричний метод.
Студент повинен вміти:
• Обчислювати визначники;
• Виконувати дії з матрицями;
• Знаходити обернену матрицю;
• Розв’язувати систему рівнянь методом Гаусса і Крамера, а також
матричним методом.

3.

Визначники
a11
a21
a12
a11 a22 a21 a12- визначник другого порядку
a22
a11
a21
a31
a12
a22
a32
a13
a23 - визначник третього порядку
a33
Розклад визначника за рядком або стовпцем:
a11
a21
a31
a12
a22
a32
a21
a13
a31
a13
a23
a23 a11
a32
a33
a22
a32
a23
a21
a12
a33
a31
a23
a33

4.

1. Визначник не зміниться, якщо його рядки замінити відповідними стовпцями.
2. Якщо переставити місцями два рядки (стовпці), то визначник змінить знак.
3. Якщо один з рядків (стовпців) визначника складається тільки з нулів, то
визначник дорівнює нулю.
4. Якщо визначник має два однакових рядки (стовпці), то він дорівнює нулю.
5. Спільний множник, що міститься в усіх елементах одного рядка (стовпця),
можна винести за знак визначника.
6. Якщо у визначнику елементи двох рядків (стовпців) пропорційні, то
визначник дорівнює нулю.
7. Якщо кожен елемент n-го рядка (n-го стовпця) є сумою двох доданків, то
такий визначник дорівнює сумі двох визначників, у одного з яких n-й рядок (nй стовпець) складається з перших доданків, а у другого – з других; інші
елементи всіх трьох визначників однакові.
8. Визначник не зміниться, якщо до елементів одного рядка (стовпця) додати
відповідні елементи іншого рядка (стовпця), помножені на одне й те саме
число.

5.

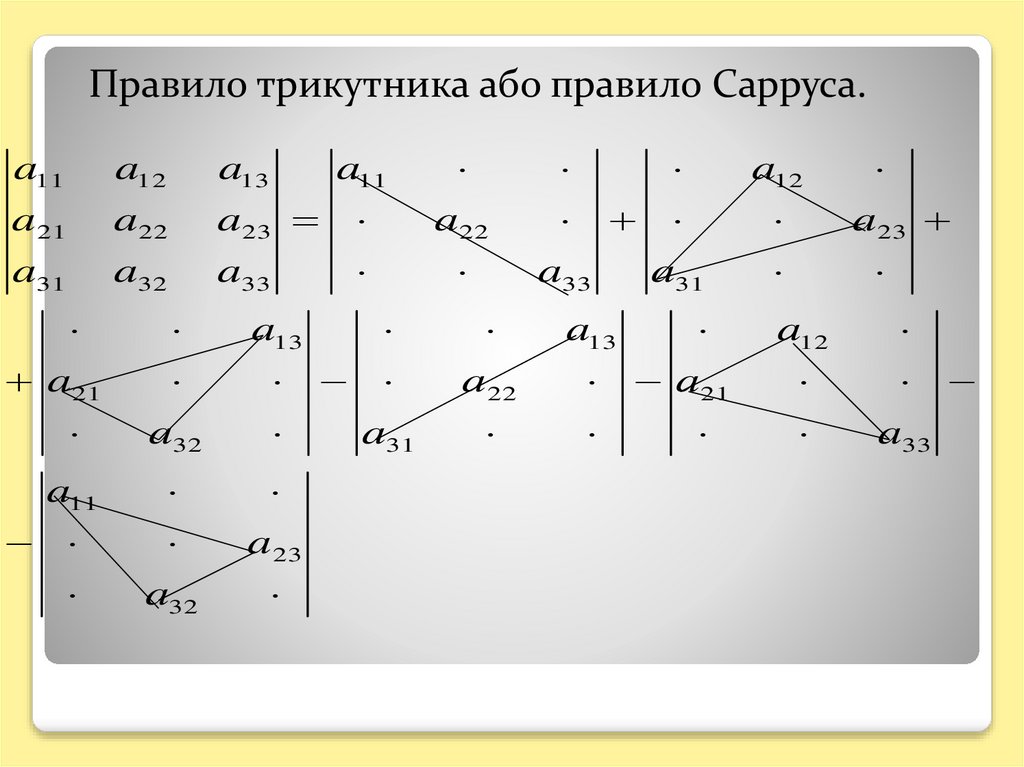
Правило трикутника або правило Сарруса.
a11
a21
a31
a12
a22
a32
a13
a11
a23
a33
a21
a32
a13
a31
a11
a32
a23
a22
a22
a33
a31
a13
a21
a12
a12
a23
a33

6.

a11
a21
a31
a12
a22
a32
a
13
a
11
a
a23
a33
a21
a31
a22
a32
12
Мінором M ij елемента a ij визначника 3-го порядку
називається визначник другого порядку, одержаний після
викреслювання і-го рядка і j-го стовпчика, на перетині яких
знаходиться даний елемент.
Алгебраїчним доповненням Aij
елемента a ij називається
мінор цього елемента, взятий із знаком "+", якщо сума номера рядка і
стовпчика ( i + j ), де знаходиться даний елемент, є число парне, та із
знаком “ - “, якщо це число непарне.
Aij ( 1)i j M ij

7.

Матриці
Матрицею розміру m × n називається прямокутна таблиця з m × n чисел
aij , i 1, m, j 1, n.
a11
a21
A
a
m1
a12
a22
am 2
a1n
a2 n
amn
a ij - елементи матриці А, де і – номер рядка, а j – номер стовпця.
Якщо m = n , то А називається квадратною матрицею.
a11 , a22 , , amn- головна діагональ ( Рис. 2).
Квадратна матриця, у якої на головній діагоналі стоять одиниці, а всі
інші елементи дорівнюють 0 – називається одиничною ( Рис. 1).
1 0 0 0
0 1 0 0
E
0 0 0 1
Рис. 1
a11 0 0
0
a
0
22
0
0 amn
Рис. 2

8.

Матриця називається нульовою, якщо всі її елементи дорівнюють 0.
0 0 0 0
0 0 0 0
0
0 0 0 0
Дії над матрицями
Сумою (різницею) двох матриця А і В називається матриця С, елементи
якої рівні сумі (різниці) відповідних елементів матриць А та В. A ( aij )
і B (bij )
Cij aij bij , i 1, m, j 1, n.
С=А±В
a11
a
A 21
a
m1
a12
a22
am 2
a1n
a2 n
amn
b11
b21
B
b
m1
b12
b22
bm 2
b1n
b2 n
bmn

9.

a11 b11 a12 b12 a1n b1n
a21 b21 a22 b22 a2 n b2 n
C A B
a b
a
b
a
b
m
1
m
1
m
2
m
2
mn
mn
А+В=В+А;
А+О=А;
О+А=А.
Матриці А і В називаються протилежними, якщо їх сума А+В=О є
нуль-матриця.
Добутком матриці на число називається матриця елементами
якої є добутки елементів даної матриці на це число:
a11
a21
A A
a
m1
a12 a1n a11
a22 a2 n a21
am 2 amn am1
a12 a1n
a22 a2 n
am 2 amn

10.

Операція множення матриці на число має розподільну
властивість.
λ ( А + В ) = λА + λВ
Якщо λ = О, то А · О дорівнює нуль-матриці А · О = О · А = О.
Добутком двох матриць А і В, число стовпців першої з яких
дорівнює числу рядків другої, називається третя матриця С,
елемент якої дорівнює сумі добутків елементів і-го рядка матриці
А на відповідні елементи j-го стовпця матриці В.
a11
a21
A
a
m1
a12 a1n
a22 a2 n
am 2 amn
b11 b12 b1 p
b21 b22 b2 p
B
b
b
b
n
1
n
2
np

11.

c11
c21
C A B
c
m1
c12 c1 p
c22 c2 p
cm 2 cmp
n
де
cij ai1b1 j ai 2b2 j ainbnj aijbij
i 1
i 1,2,3, , m
1. A · 0 = 0
2. A · E = A
3. A · B = B · A
j 1,2,3, , p

12.

Обернена матриця
Оберненою для заданої квадратної матриці А називається така
матриця A 1 , добуток на яку матриці А рівний одиничній матриці,
тобто
1
1
A A E,
або
A A E.
Схема знаходження оберненої матриці для заданої квадратної матриці.
a11
a21
A
a
n1
a12
a22
an 2
a1n
a2 n
ann
I. Обчислимо визначник матриці А (|А|).
ІІ. Транспонуємо матрицю А, тобто одержуємо матрицю:
a11
a12
A
a
1n
a21
a22
a2 n
an1
an 2
ann

13.

ІІІ. Знаходимо алгебраїчні доповнення кожного елемента
транспонованої матриці А´ і записуємо їх у вигляді матриці
(приєднана)
a11
a12
A
a
1n
a21
a22
a2 n
an1
an 2
ann
IV. Поділимо кожен елемент матриці A на визначник
матриці |А|. Одержана матриця буде оберненою.
a11
1
1 a12
1
A
A
A
A
a
1n
a21
a22
a2 n
an1
an 2
ann
A

14.

Розв’язування систем лінійних рівнянь
різними способами
a11x1 a12 x2 a1n xn b1
a x a x a x b
21 1 22 2
2n n
2
...........................................
am1 x1 am 2 x2 ann xn bn
(1) – система m лінійних
рівнянь з n - невідомим
Розв’язком системи лінійних алгебраїчних рівнянь (1)
називають таку сукупність чисел 1 , 2 , n , яка
перетворює всі рівняння системи (1) у числові тотожності.

15.

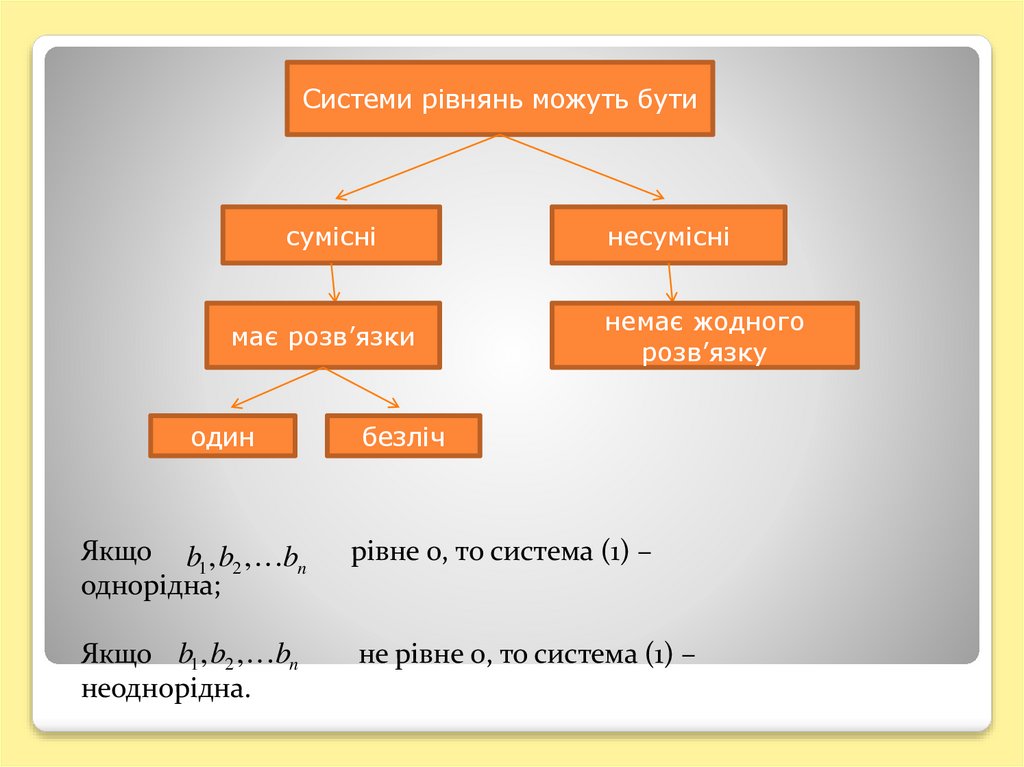
Системи рівнянь можуть бути
сумісні
має розв’язки
один
несумісні
немає жодного
розв’язку
безліч
Якщо b1 , b2 , bn
однорідна;
рівне 0, то система (1) –
Якщо b1 , b2 , bn
неоднорідна.
не рівне 0, то система (1) –

16.

Основна матриця
системи рівнянь
a11a12 a1n
a21a22 a2 n
A
(2)
...................
a a a
nn
m1 m 2
Розширена матриця
системи рівнянь
a11a12 a1n b1
a21a22 a2 n b2
B
(3)
...................
a a a b
nn
m
m1 m 2
Способи розв’язування систем рівнянь
Системи рівнянь з
двома змінними
1) Спосіб підстановки;
2) Спосіб додавання;
3) Спосіб графічний.
Системи рівнянь
з трьома і більше змінними
1) Метод Крамера;
2) Метод Гаусса;
3) Спосіб матричний.

17.

Крамер народився в сім'ї лікаря. З
раннього віку показав великі здібності до
математики. У 18 років захистив
дисертацію. У 20-річному віці Крамер
виставив свою кандидатуру на вакантну
посаду викладача на кафедрі філософії
Женевського університету.
У 1727 р. Крамер скористався цим
правом і 2 роки мандрував по Європі,
переймаючи досвід у провідних
математиків — Йоганна Бернуллі,
Галлея і де Муавра та інших.
Повернувшись, він вступає з ними в
листування, яка тривала все його
недовге життя.
У вільний від викладання час Крамер
пише статті на різні теми: геометрія,
історія математики, філософія,
застосування теорії ймовірностей. У
1751 р. Крамер отримує серйозну
травму після дорожнього інциденту з
каретою і 4 січня 1752 р. Крамер вмирає.

18.

Спосіб Крамера (для випадку m=n)
a11a12 a1n
a21a22 a2 n
...................
an1an 2 ann
b1a12 a1n
b2 a22 a2 n
1
...................
bn1an 2 ann
a11b1 a1n
a21b2 a2 n
2
...................
an1bn ann
a11a12 b1n
a21a22 b2 n
3
...................
an1an 2 bnn
1
X1
;
2
X2
;
;
n
Xn
;

19.

Характерними рисами досліджень
Гаусса є надзвичайна їх різнобічність і
органічний зв'язок у них між теоретичною і
прикладною математикою.
Карл Фрідріх народився 30 квітня 1777
р. у Брауншвейгу. У 1784 р. Карла віддали
до народної школи. Після чотирирічного
навчання в школі Гаусс перейшов до гімназії
відразу в другий клас. З 1795 р. хлопець
став студентом Геттінгенського
університету. У 1806 р. Карла призначають
професором в Геттінгені.
У 1810 р. Гаусс отримує премію
Паризької академії наук і золоту медаль
Лондонського королівського товариства. У
1815 р. публікує перше строге доведення
основної теореми алгебри. У 1824 р.
обирається іноземним членом
Петербурзької Академії наук.
23 лютого 1855 р. великого математика
не стало.

20.

Метод Гаусса (метод послідовного включення змінних
перетворенням розширеної матриці до трикутного вигляду).
(1)
a11a12 a1n b1
a21a22 a2 n b2
..........................
a a a b
mn
m
m n2
зводимо її до вигляду
a11a12a13 a1n b1
0a22a12 a2 n b2
0 0a a b
12
3n
3
................................
0 0 0 a b
mn
m
a11a12 a1n b1
0
a
a
b
22
2n
2
0 0 a b
3n
3
................................
0 0 0 b
m
a11a12 a1n b1
0
a
a
b
22
2n
2
0 0 a b
3n
3
................................
0 0 0 0
1 розв’язок
О
безліч розв’язків

21.

Матричний метод
Нехай дано систему (1) (для випадку m=n)
А – основна матриця, Х – матриця стовпець із невідомих, В –
матриця стовпець із вільних членів.
a11a12 a13 a1n
a21a22 a12 a2 n
A
...................
a a a a
nn
n1 n 2 12
x1
x2
X
x
n
b1
b2
B
b
n

22.

Перепишемо систему (1) у вигляді матричного рівняння А · Х =
В.
1
Його розв’язок X A B - називається матричним розв’язком
системи лінійних рівнянь.
(1)знаходимо визначник |А|
якщо |А| ≠ 0 – це неособлива матриця, до неї існує
обернена.
(2) шукаємо обернену матрицю
знаходимо визначник матриці А
транспонуємо матрицю А; і позначаємо іі A
складаємо матрицю з алгебраїчних доповнень до
елементів матриці A і позначаємо A
поділимо матрицю на визначник даної матриці і
1
отримаємо A
A 1
1
A

23.

1. Які основні властивості визначників?
2. Що таке мінор та алгебраїчне доповнення до елемента
визначника? Як їх знайти?
3. Які дії виконують із матрицями?
4. Як знайти матрицю, обернену до даної?
5. Що називається рангом матриці?
6. У чому полягає суть методу Гаусса?
7. Коли можна застосовувати правило Крамера?