Similar presentations:
Комплексні числа
1. Комплексні числа
КОМП’ЮТЕРНІЧИСЛЕННЯ
ЕЛЕМЕНТИ ЛІНІЙНОЇ АЛГЕБРИ
1. МОДУЛЬ
Основні 1.
поняття
2. Геометричне зображення комплексних чисел
3. Тригонометрична форма запису
комплексних чисел
4. Дії над комплексними числами
5. Показникова форма комплексного числа
ЛЕКЦІЯ 1. МАТРИЦІ ТА ВИЗНАЧНИКИ
Трунова Олена Василівна
доцент, к. пед. н.
2.
• Звітність в семестрі до 80 балів:ТЕСТИ - 5 балів (5*4=20)
ЛР - 5 балів (5*4=20)
РГР - 5 балів (5*4=20)
МКР - 10 балів (10*2=20)
Додкові бали конспект лекцій – до 3
Допуск до іспиту не менше 19 балів
Іспит 20 балів
Задавайте питання по ходу лекцій і на ЛЗ.
Підготовка до ЛЗ, іспитів.
Робота з підручниками.
Консультації в семестрі.
Консультації в сесію.
Відповіді на лабораторних заняттях.
Участь в олімпіадах.
3. Література
Вища математика: навч. посіб. для студ. вищ. навч. зак. / В.П Дубовик., I.I. Юрик. – 4-те вид. – К.: Ігнатекс-Україна., 2013. – 648 с:
Вища математика: Підручник. У 2 ч. Ч. 1: Лінійна і векторна алгебра: Аналітична геометрія: Вступ до математичного аналізу: Диференціальне і
інтегральне числення /П.П. Овчинников, Ф.П. Яремчук, В.М. Михайленко; За заг. ред. П.П. Овчинникова; Пер. з рос. П.М. Юрченка. — 3-те вид.,
випр. – К.: Техніка, 2007. – 600 с.
Вища математика: Підручник. У 2. Ч. 2: диференціальні рівняння. Операційне числення. Ряди та їх застосування. Стійкість за Ляпуновим.
Рівняння математичної фізики. Оптимізація та керування. Теорія ймовірностей. Числові методи; за заг. ред. П.П. Овчинникова; пер. з рос. Є.В.
Бондарук, Ю.Ю. костриці, Л.П. Оніщенко. – 3-тє вид., випр. – К.: Техніка, 2004 . – 792 с.
Дубовик В.П. Вища математика: навч. посібн. / Дубовик В.П., Юрик І.І. – К.: Ігнатекс-Україна, 2013. – 648 с. – Режим доступу:
https://opac.kpi.ua/F/ER5L2BH454XJ2XCGY41CV6FJ28CCXQY8UFDTQ4GS83UY8GRPYB-62054?func=full-setset&set_number=514442&set_entry=000010&format=999
Дороговцев, А.А. Математичний аналіз : підручник : у 2-х ч. Ч. 1 / А.А. Дороговцев. – К. : Либідь, 1993. – 320 С.
Дороговцев, А.Я. Математичний аналіз : у 2-х ч. Ч. 2 / А.Я. Дороговцев. – К.: Либідь, 1994. – 304 С.
Математика в технічному університеті: Підручник / І. В. Алєксєєва, В. О. Гайдей. О.О. Диховичний, Л. Б. Федорова; за ред. О.І. Клесова; КПІ ім.
Ігоря Сікорського. – Київ: Видавничий дім «Кондор», 2018.–Т.1. – 496 с. – Режим доступу: https://ela.kpi.ua/handle/123456789/24338
Математика в технічному університеті [Електронний ресурс]: підручник / І. В. Алєксєєва, В. О. Гайдей, О. О. Диховичний, Л. Б. Федорова; за ред.
О. І. Клесова ; КПІ ім. Ігоря Сікорського. – Київ: Видавничий дім «Кондор», 2019. – Т.2. – 504 с. – Режим доступу:
https://ela.kpi.ua/handle/123456789/30396
Паранчук Я. С., Мороз В. І. Алгоритмізація та програмування. MathCAD. Навчальний посібник. Друге видання. Львів: Видавництво Львівської
політехніки, 2012. – 312 с.
Додаткова література
Dennis G. Zill. (2016) Advanced Engineering Mathematics. Jones & Bartlett Publishers –1024 p. – Режим доступу: https://elasticbeanstalk-us-east-2344375731421.s3.us-east-2.amazonaws.com/StudyChat/Dennis-G.-Zill-Advanced-Engineering-Mathematics-2016-Jones-Bartlett.pdf
Introduction to Mathcad 15 Larsen, Ronald W. [Prentice Hall, 2010] (Paperback) 3rd Edition
Kreyszig, E. Kreyszig, H. and Norminton, E. J. (2011) Advanced Engineering Mathematics. 10th edition, Wiley, NY. – 1152 p. – Режим доступу:
https://soaneemrana.org/onewebmedia/ADVANCED%20ENGINEERING%20MATHEMATICS%20BY%20ERWIN%20ERESZIG1.pdf
4. Квантори, Позначення І скорочення
КВАНТОРИ, ПОЗНАЧЕННЯ ІСКОРОЧЕННЯ
] – нехай;
( ) – і;
– або;
– не;
– для довільного, для всіх;
: – такій, що;
– існує;
! – єдиний;
– наближається;
– випливає, отже;
– тоді і тільки тоді;
– сума;
– добуток;
– знак об'єднання;
– знак перетину;
5. Зміст 1. Матриці та їх властивості 2. Лінійні операції над матрицями 3. Визначники та їх властивості
6.
Термін «матриця»започаткував англійський
математик
Джеймс Джозеф Сильвестр.
1814–1897
«Математика – музика
розуму».
Джеймс Джозеф Сильвестр
7.
§1 МАТРИЦІ ТА ВИЗНАЧНИКИ1.1 Матриці та їх властивості
Матрицею розміру m n називається сукупність чисел,
розташованих у вигляді таблиці з m рядків і n стовпчиків:
a11
a
A 21
.
am1
a12
a22
.
am 2
...
...
.
...
a1n
a2 n
.
.
amn
Числа аij , що складають матрицю, називаються елементами
матриці, до того ж і – номер рядка, а j – номер стовпчика. Якщо
m≠n, то матриця називається прямокутною. Якщо m=n, то матриця
называється квадратною порядку n.
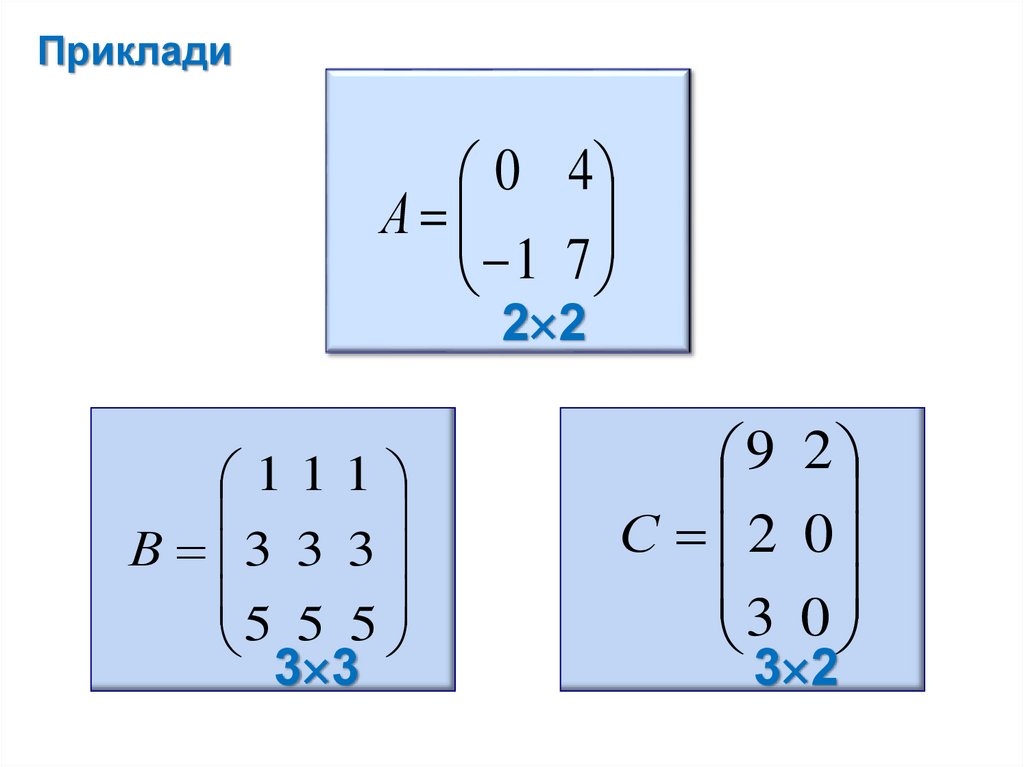
8. Приклади
0 4А
1 7
2 2
111
В 3 3 3
5 5 5
3 3
9 2
С 2 0
3 0
3 2
9.
a1a
Матриця розміру m 1 виду 2 , що складається з одного стовпця
am
називається вектор-стовпець, а матриця A=[a1 a2…an]
розміру
1 n, що складається з одного рядка – вектор-рядок.
У випадку квадратної матриці
a11 a12 ... a1n
a
a
...
a
22
2n
A 21
.
.
.
.
an1 an 2 ... ann
елементи a11, a22,…ann утворюють головну діагональ, а елементи
an1, an-1 2,…a1n – побічну діагональ матриці.
10.
Квадратна матриця, в якої всі елементи aij дорівнюють 0називається нульовою матрицею.
0 ... 0
Оmxn ... ... ...
0 ... 0
Матриця
1 0 ... 0
0 1 ... 0
називається одиничною.
E
. . . .
0
0
0
1
11.
10
Е2 diag 1, 1 0 1
Еn diag 1, 1, ...,1
1 0 0
Е3 diag 1, 1, 1 0 1 0
0 0 1
11
12.
Квадратна матриця називається трикутною,якщо всі елементи, розташовані по один бік від
головної діагоналі, дорівнюють нулю.
Приклади.
верхньотрикутна
нижньотрикутна
111
А 0 3 3
0 0 5
7
B
1
0
5
13.
Матриця АТ , отримана з даной матриці А шляхомзаміни рядків на стовпчики, і навпаки, називається
транспонованою.
Позначається AT.
Приклад
0 3
А 1 4 АT 0 1 2
3 4 5
2 5
(АТ)Т=А
14.
• Якщо AT = A то матрица A називається симетричною.• Приклад
1
2
3
1 2 3
Т
С 2 3 0 С 2 3 0 C
3 0 5
3 0 5
15.
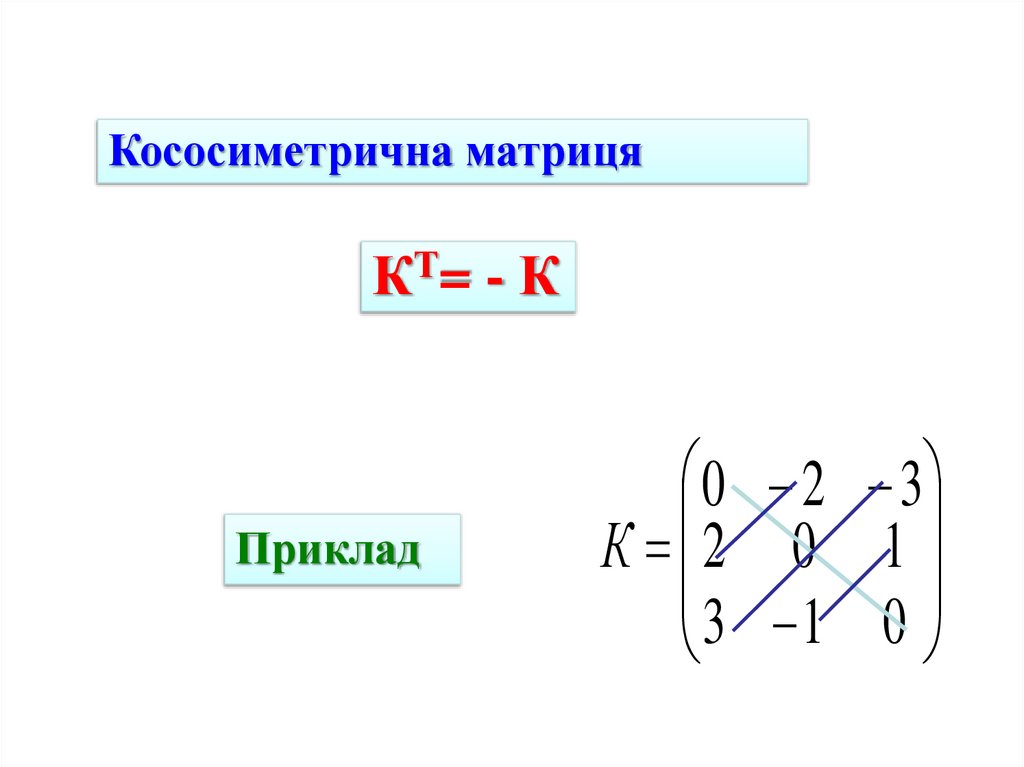
Кососиметрична матрицяКТ= - К
Приклад
0 2 3
К 2 0 1
3 1 0
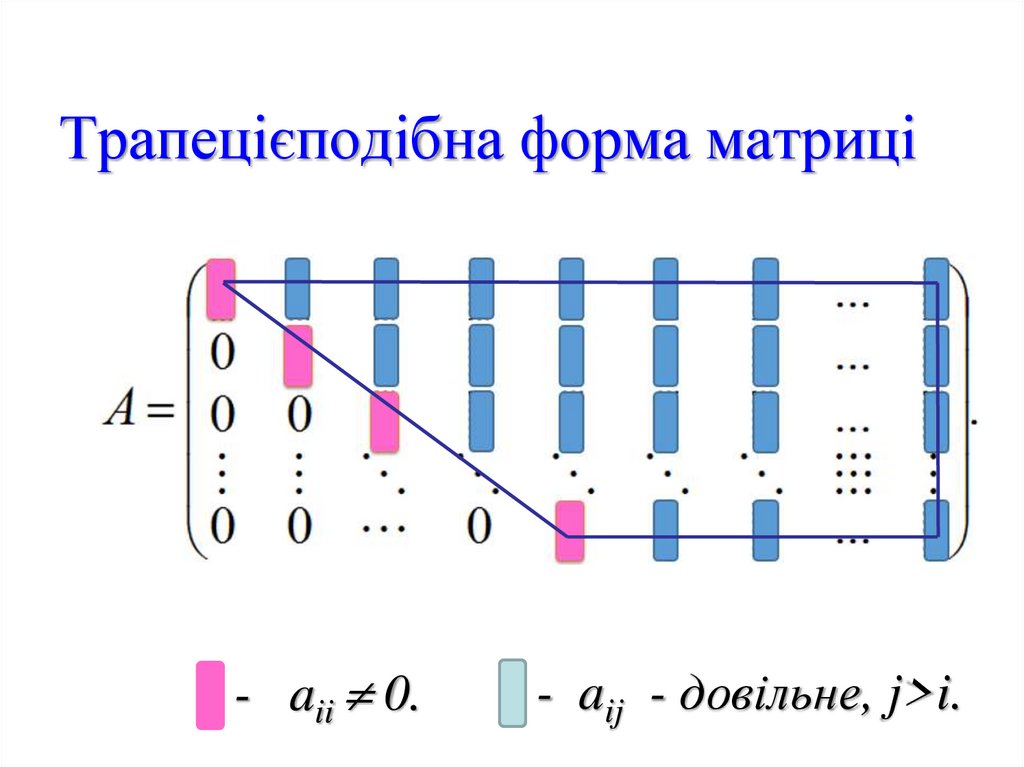
16. Трапецієподібна форма матриці
- aii 0.- aij - довільне, j>i.
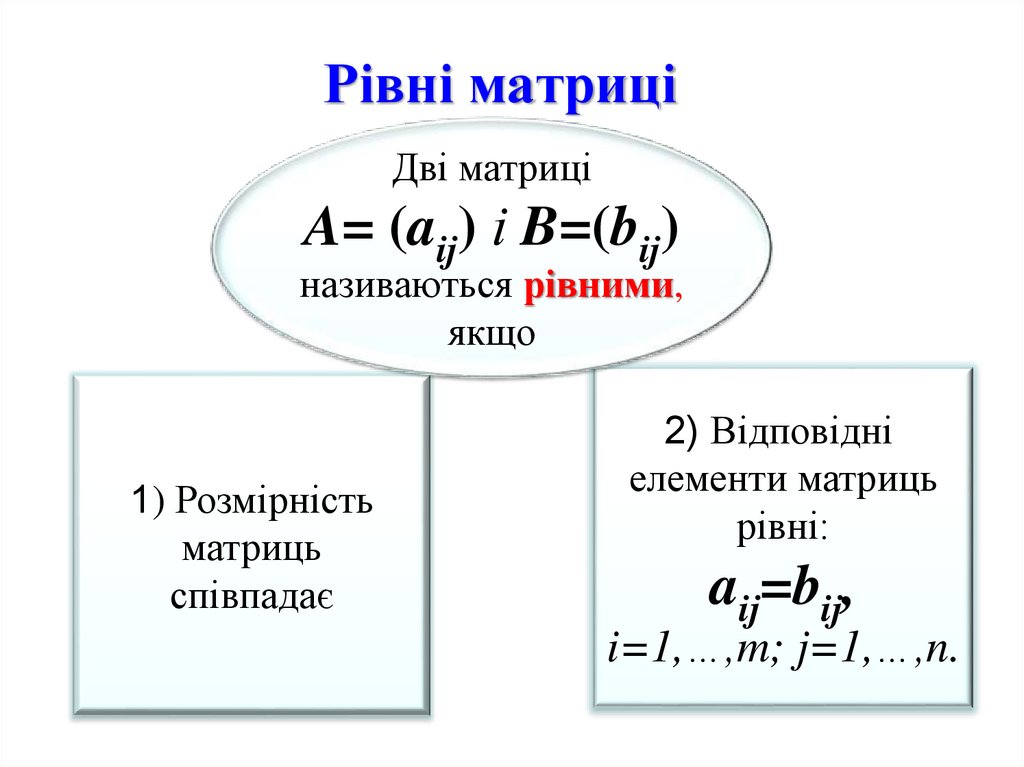
17. Рівні матриці
Дві матриціA= (aij) і B=(bij)
називаються рівними,
якщо
1) Розмірність
матриць
співпадає
2) Відповідні
елементи матриць
рівні:
aij=bij,
i=1,…,m; j=1,…,n.
18.
1.2. Лінійні операції над матрицями ДодаванняДля того, чтоб додать дві матриці
A і B (одинакової
розмірності) необхідно додать їх відповідні елементи.
Для того, чтобы знайти різницю матриць А і В (одинакової
розмірності) необхідно від кожного елемента матриці А відняти
відповідний елемент матриці В.
Матриця -А (мінус А)називається матрицею протилежною А.
2 5 6
Приклад: Нехай A
,
0 4 1
Тоді
1 7 10
A B
,
6
0 9
2 5 6
A
.
0 4 1
3 2 4
B
.
0 5 7
5 3 2
A B
,
0 1 8
19.
Множення на числоДля того, чтоб помножити матрицю А на число R необхідно
кажен элемент матриці помножить на число .
2 5 6
Приклад: Нехай A
,
0 4 1
тоді
4 10 12
2 A
.
0 8 2
20.
Множення на вектор-стовпчикДля множення матриці
А(m n) на вектор-стовпчик Х(n 1)
необхідно, щоб число стовпців n матриці А дорівнювало числу
елементів вектора-стовпчика х (n 1). Тоді добуток матриці А на
вектор-стовпець Х позначається АХ і дорівнює
a11 a12 ... a1n x1 a11 x1 a12 x2 ... a1n xn
a
x a x a x ... a x
a
...
a
22
2n 2
2n n
AX 21
21 1 22 2
.
.
.
.
.
...
am1 am 2 ... amn xn am1 x1 am 2 x2 ... amn xn
21. Множення матриці на стовпчик Кожен рядок матриці скалярно множиться на стовпець
3 1 2 8 3 8 1 7 2 2 214 2 0 7 4 8 2 7 0 2 46
5 6 1 2 5 8 6 7 1 2 4
22.
Множення двох матрицьa11 a12 ... a1n
a
a
...
a
21
22
2n
Нехай A
.
.
.
.
a
a
...
a
mn
m1 m 2
і
b11 b12 ... b1k
b
b22 ... b2 k
21
B
.
.
.
.
b
b
...
b
nk
n1 n 2
розмірності m n і n k відповідно, (узгоджені матриці) тобто –
число стовців матриці А дорівнює числу рядків матриці В.
Добутком матриці А на матрицю В називається матриця
С(m k) з елементами сij, що дорівнюють сумі добутків елементів iго рядка матриці А на відповідні елементи j-го стовпця матриці В,
сij=ai1b1j+ai2b2j+…+ainbnj,
i=1,...,m; j=1,...,k.
23. Приклад
Знайти добуток матриць2 6 1 2 0
1 2 0 . 1 3
2 2 6 ( 1)
2 0 6 3
2 1 6 0
1 1 ( 2) 0 1 2 ( 2) ( 1) 1 0 ( 2) 3
2 2 18
1 4 6
24.
25.
A B B AУзагалі, якщо добутки АВ і ВА існують, то АВ ВА.
Якщо АВ = ВА, то такі матриці називаються комутативними
(перестановочними).
Приклад.
25
26.
За умови, що операції в обох частинах рівностіздійсненні, справедливі наступні властивості.
Властивості добутку матриць
1. А · О = О;
2. А · Е = А;
3. А · В ≠ В · А;
4. α (АВ) = (αА) · В = А · (αВ);
5. АВС = (АВ) · С = А · (ВС);
6. А (В + С) = АВ + АС;
7. (А · В)Т =ВТ · АТ.
27.
Вільгельм ГотфрідЛейбніц
(1646-1716) — саксонський
філософ, логік, математик
,
механік, фізик, юрист,
історик, дипломат,
винахідник і мовознавець.
Поняття «визначник»
належить Г. Лейбніцу (1678).
28.
1.3 Визначники та їх властивостіПоняття визначника (детермінанта) вводиться тільки для
квадратних матриць. Познпчення |A|, det A, .
Визначником n-го порядку матриці А називається алгебраїчна
сума добутків елементів, взятих точно по одному з кожного рядка
і
кожного
стовпчика
матриці
А.
Знак
кожного
доданка
визначається спеціальним правилом.
Визначник n-го порядку містить n! членів.
a11
A
a 21
Приклад:
a12
= a11a22- a12a21 – визначник другого порядку.
a 22
2 5
A
2 7 ( 5) 3 14 ( 15) 29.
3 7
29.
• Квадратна матриця А називається невиродженою,якщо її визначник det А 0.
• У протилежному випадку (det А = 0) матриця А
називається виродженою.
30.
a11A a21
a31
a12
a22
a32
a13
a23 a11a22a33+a12a23a31+ a13a21a32- a13a22a31-a11a23a32a33
-a12a21a33 – визначник третього порядку.
Правило трикутника : три додатних члена визначника третього
порядку є добутком елементів головної діагоналі і елементів, що
знаходяться в вершинах двох рівнобедрених трикутників, основи яких
паралельні головній діагоналі. Три його від'ємних члена є добутком
елементів побічної діагоналі і елементів, що знаходяться в вершинах
двох рівнобедрених трикутників, основи яких паралельні побічної
діагоналі.
«+»
«-»
31.
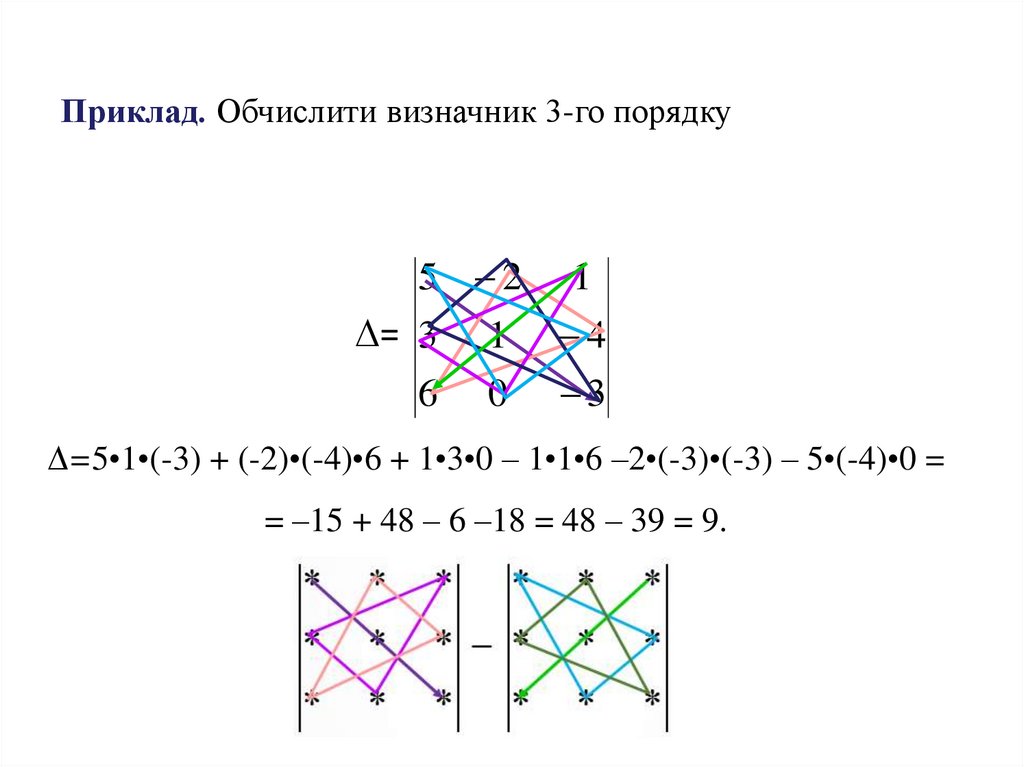
Приклад. Обчислити визначник 3-го порядку5 2 1
= 3 1 4
6 0 3
=5•1•(-3) + (-2)•(-4)•6 + 1•3•0 – 1•1•6 –2•(-3)•(-3) – 5•(-4)•0 =
= –15 + 48 – 6 –18 = 48 – 39 = 9.
32.
Приклад. Обчислити визначник 3-го порядкуЗа допомогою правила діагоналей
5 2 1
= 3 1 4
6 0 3
-
-
-+ + +
=5•1•(-3) + (-2)•(-4)•6 + 1•3•0 – (1•1•6 + 5•(-4)•0 +(-2)•3•(-3)) =
= –15 + 48 – (6+18) =33 – 24 = 9.
33. Визначник довільної трикутної матриці дорівнює добутку елементів головної діагоналі
34.
Властивості визначників n-го порядку:1. Визначник матриці А дорівнює визначнику транспонованою
матриці,
А АТ .
2. Якщо всі елементи деякого рядка матриці А дорівнюють 0, то
визначник дорівнює 0.
3. Загальний (спільний) множник всіх елементів рядка визначника
можна винести за знак цього визначника.
4. Якщо у визначнику поміняти місцями два рядки, то він змінить
знак на протилежний.
5. Якщо визначник має два рівні рядки, то він дорівнює 0.
6. Якщо елементи двох рядків визначника пропорційні, то
визначник дорівнює 0.
35.
7. Значення визначника не зміниться, якщо до елементів його рядкадодати відповідні елементи іншого рядка, помножені на одне і те
ж число k.
Мінором Мij елемента aij називається визначник (n-1) порядку,
отриманний викресленням з визначника n-го порядку елементів i-го
рядка та j-го стовпця, i, j = 1,...,n.
Приклад: 2 1 4
A 6
0
2 1
( 2) 3 1 0 6 – мінор
2 8 , M 23
0 3
3 6
елемента а23.
Алгебраїчним доповненням елемента aij називаєтьчя число
Aij=(-1)i+j Мij.
A23=(-1)2+3 М23=(-1)(-6)=6.
36.
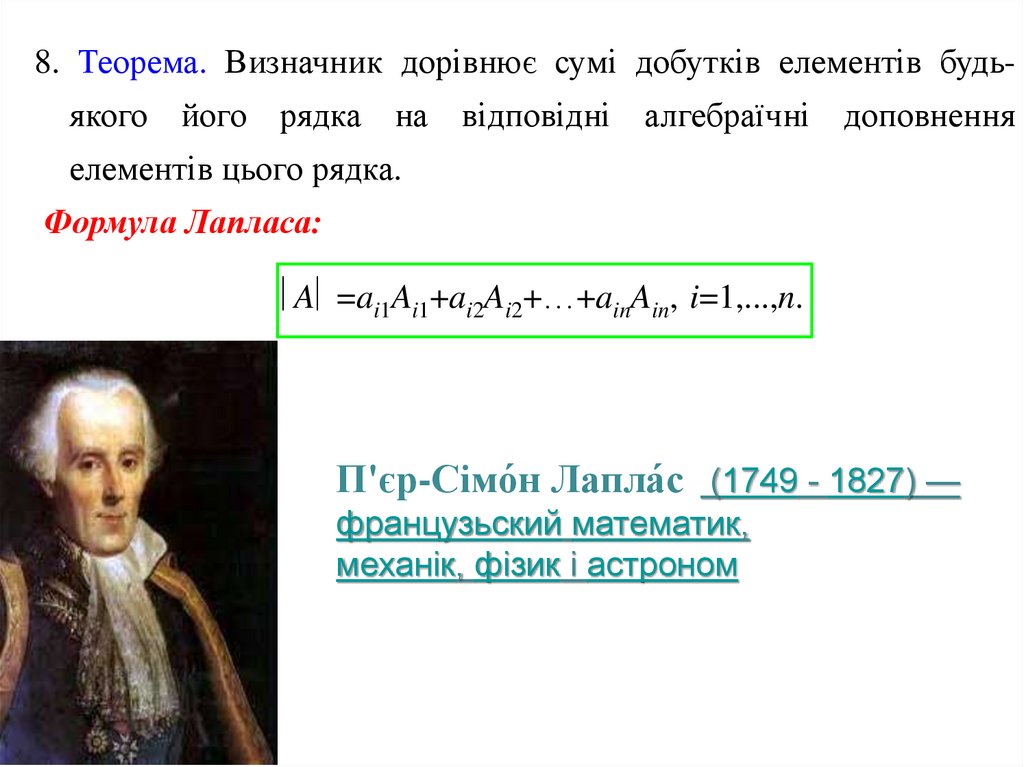
8. Теорема. Визначник дорівнює сумі добутків елементів будьякого його рядка на відповідні алгебраїчні доповненняелементів цього рядка.
Формула Лапласа:
A =ai1Ai1+ai2Ai2+…+ainAin, i=1,...,n.
П'єр-Сімо́н Лапла́с (1749 - 1827) —
французьский математик,
механік, фізик і астроном
37.
2 1 14 3
1 1
2 4 3 2
2
17 12
17 12
11 17 12
1 1
11
2( 48 51) 2(12 17 ) 11(3 4)
4 3
6 10 11 5.
4 1
3 5
2 3
5 0
0 3
4 1
3
2 4
4 1
1 3
2 2 3 1 2 5
5
0 1
3
1
2
3
5 0 5
0 5
2(5 10 5 ( 14)) 2(50 70) 2 120 240
38. Правило чужих доповнень
• Сума добутків елементів будь-якого ряду кв. матриці наалгебраїчні доповнення відповідних елементів іншого її
паралельного ряду дорівнює нулю.
39.
9. Якщо елементи будь-якої ряду квадратної матриці Аскладаються з двох доданків, то визначник А дорівнює сумі
визначників двох матриць, що розрізняються між собою
тільки елементами цього ряду, що були раніше окремими
складовими.
а11
а12 а13 а11
а12 а13 а11
а12 а13
а11
а 21
а 22 а 23 а 21
а 22 а 23 а 21
а 22 а 23 .
а 21
а31
а32 а33 а31
а32 а33 а31
а32 а33
а31
det Е 1
det( A B) det A det B
40.
«А математику тільки тому вчити слід,що вона розум до ладу приводить».
М. В. Ломоносов









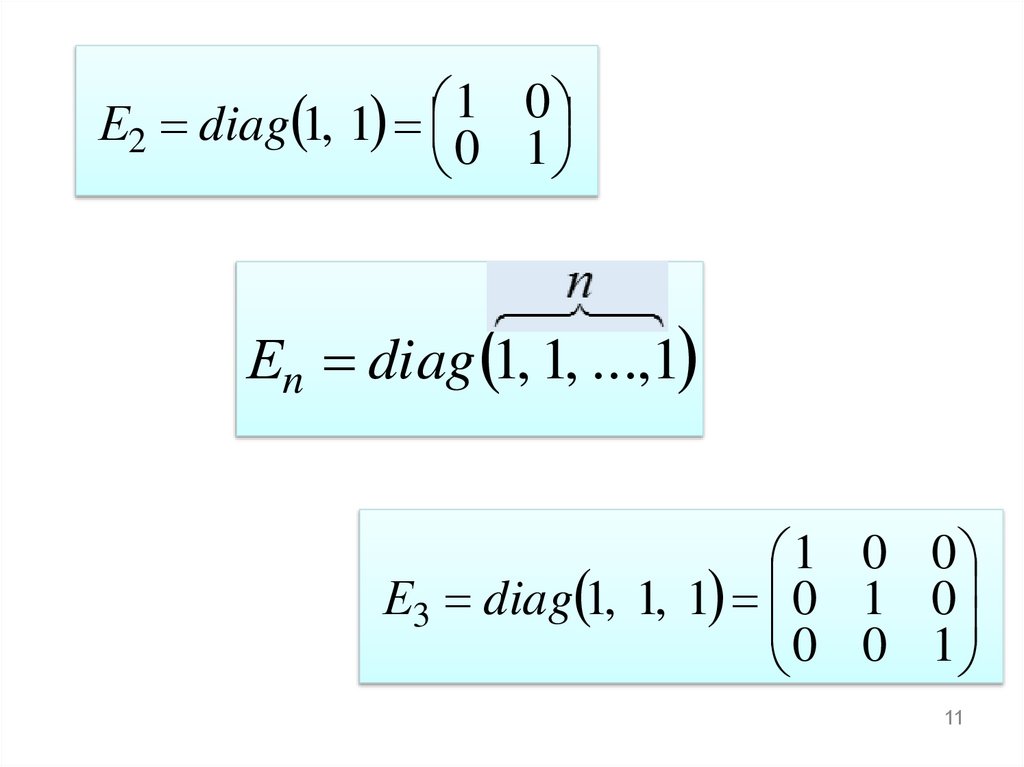




















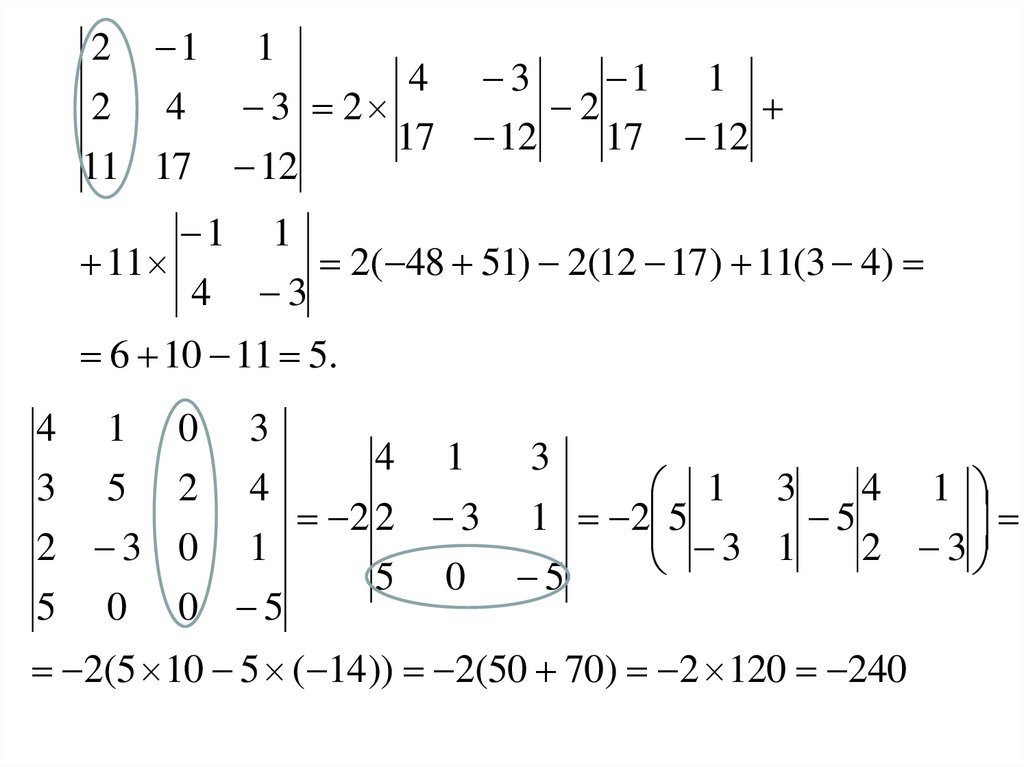



 mathematics
mathematics








