Similar presentations:
Методи розв’язування СЛАР (Система лінійних алгебраїчних рівнянь)
1. МЕТОДИ РОЗВ’ЯЗУВАННЯ СЛАР
a11 x1 a12 x 2 ... a1n x n b1 ,a x a x ... a x b ,
21 1
22 2
2n n
2
..............................................
a n1 x1 a n 2 x2 ... a nn x n bn ,
або
n
a
j 1
ij
x j bi , i 1,..., n.
Система лінійних алгебраїчних рівнянь у матричній формі Ах = b,
a11 a12 ... a1n
де
b1
x1
a a ...a
b
x
21
22
2
n
2 ,
2
A
b
x
..................
:
:
an1 an 2 ...ann
b
n
xn
2. МЕТОДИ РОЗВ’ЯЗУВАННЯ СЛАР
Методи чисельного розв’язування СЛАР діляться на дві групи:прямі та ітераційні.
В прямих (або точних) методах розв’язок x системи знаходиться
за скінчену кількість арифметичних дій (методи Гаусса, LUрозкладання, прогонки, Халецького и т.д). Якщо матриця
неособлива, тобто
a11 a12 ... a1n
detA
a21 a22 ... a2 n
....................
0,
an1 an 2 ... ann
то x = A-1b, де A-1 − обернена матриця.
A A-1 = A-1 A = E
Ітераційні методи полягають в тому, що розв’язок x системи
знаходиться як границя послідовних наближень x(k) при k , де
k − номер ітерації (Якобі, Зейделя, варіаційного типу).
3.
4. ПРЯМІ МЕТОДИ РОЗВ’ЯЗУВАННЯ СЛАР МЕТОД ГАУССА
Прямий хід методу Гаусса полягає в послідовному виключенніневідомих x1,x2,…,xn з системи. Якщо a11 0, то поділивши
перше рівняння системи на a11 , отримаємо:
x1 c12 x 2 ... c1n x n y1 ,
де
a1 j
c1 j
, j 2, 3, ..., n,
a11
b1
y1
.
a11
Помножимо це рівняння на a i1 і відніматимемо отримане
рівняння від i-го рівняння системи. Після виключення x1 з решти
рівнянь отримаємо:
x1 c12 x 2 ... c1 j x j ... c1n x n y1 ,
a22 x 2 ... a2 j x j ... a2 n b2 ,
(1)
(1)
...
...
...
(1)
...
(1)
...
(1)
an(1)2 x 2 ... anj(1) x j ... ann
x n bn(1) .
5. МЕТОД ГАУССА
Коефіцієнти системи обчислюються за формулами:akj( 0) akj ,
ak( k j 1)
cki
( k)
ij
a
a
( k 1)
ij
( k 1)
kk
k, j 1, ,2, ..., n,
j k 1, k 2, ..., n,
,
k 1, 2, ..., n,
( k 1)
kj
ik
a
a
c , i, j k 1, k 2, ..., n, k 1, 2, ..., n 1.
Обчислення правих частин системи здійснюється за
формулами:
( k 1)
( 0)
bk
bk ,
( k)
bi
yk
( k 1)
bi
bk
a
( k 1)
kk
( k 1)
aik
,
yk ,
k 1, 2, ..., n,
i k 1, k 2, ..., n.
6. МЕТОД ГАУССА
Виключаючи послідовно невідомі із початкової системиотримуємо систему рівнянь Cx
= y:
x1 c12 x 2 c13 x 3 ... c1n x n y1 ,
1 с12 .. ....
x 2 c23 x 3 ... c2 n x n y 2 ,
0 1.... .....
C ....................
... ... ... ... ...
x n 1 cn 1,n x n y n 1 ,
0 0 ........1
0 0... ....0
xn yn .
Зворотній хід полягає в знаходженні невідомих :
xn yn ,
xi yi
n
cij x j ,
j i 1
i n 1, n 2, ..., 1.
y1
y
с2 n
2
y .. .
сn 1, n
yn 1
y
1
n
с1n
7. МЕТОД ГАУССА
Метод Гаусса має сигнальну функцію виду (поліноміальний):f A ( n) n3 3 n2 O( n3 ).
( k 1)
Елемент akk , називається ведучим елементом на k-му кроці
виключення. Основним обмеженням методу є припущення, що
( k 1)
всі елементи akk
відмінні від нуля. Щоб зменшити похибку
ведучим необхідно вибирати найбільшим за модулем елемент.
8.
Матрицею перестановок P називається квадратна матриця, уякої в кожному рядку і в кожному стовпці наявний лише один
відмінний від нуля і рівний одиниці елемент.
Елементарною матрицею перестановок Pki називається
матриця, отримана з одиничної матриці перестановкою k-го
і i-го рядків. Наприклад, елементарними матрицями
перестановок третього порядку є матриці:
P12
1.
2.
3.
0
1
0
1
0
0
0
0 ,
1
P13
0
0
1
0
1
0
1
0 ,
0
P23
1
0
0
0
0
1
Добуток двох (а отже, і будь-якої кількості) елементарних
матриць перестановок є матрицею перестановок (не
обов’язково елементарною).
Матрицю PkiA отримують із матриці A перестановкою k-го і iго рядків.
Матрицю APki отримують із матриці A перестановкою k-го і iго стовпців.
Метод Гаусса з вибором головного елемента по стовпцю
еквівалентний звичайному методу Гаусса, який застосовують
до системи
P Ax P b
0
1 .
0
9.
З системи Ax = b маємо Cx = yМожна показати b та y пов’язані між собою як
Dy = b, де матриця D має вигляд:
a11
a
21
D a31
.
an1
З
Маємо
0
0
a22(1)
0
(1)
a33
.
a32
.
an 2(1)
( 2)
an 3( 2)
0
0
.
ann ( n 1)
0
y = D-1b
Cx = D-1b DCx = b A = DC
10.
Метод Гаусса відповідає розкладанню матриці A на добутокдвох трикутних матриць:
A = LU
(L = D, U = C)
тобто
a11
a
21
a31
...
an1
a12 ... a1n
a22 ... a2 n
a32 ... a3 n
... ... ...
an 2 ... ann
l11 0 0
l
l
0
21 22
l31 l32 l33
... ... ...
ln1 ln 2 ln 3
0 1 u12
0 0 1 u23
... 0 0 0
1
... ... ... ... ...
... lnn 0 0
0
...
...
... u1,n
... u2,n
... u3,n ,
... ...
... 1
Якщо det A ≠ 0, то існує матриця перестановок P така, що
справедливе розкладання
P A LU
11. LU-розкладання матриці А
li1 ai1 , i 1, n,aij
u1 j a1 j / a11 , j 1, n,
n
lik ukj ,
i, j 1, n
k 1
Для матриці L
j
lik ukj ,
aij
i j,
k 1
j 1
aij lij u jj lik ukj ,
j 1
звідки
k 1
lij aij lik ukj .
k 1
Для матриці U
aij
i
lik ukj ,
i <j ,
k 1
i 1
i 1
aij lii uij lik ukj ,
k 1
звідки
uij
aij lik ukj
k 1
lii
.
12. Приклад
34
1 2
2 7 12 17
;
A
3 10 22 34
4 13 28 50
1
2
L
3
4
ALU
0
3
4
5
1
2
3
4
0
0
5
6
2
3
4
5
0
1
0
0
;U
0
0
0
7
3
2
5
6
4
3
;
2
7
2
1
0
0
3
2
1
0
4
3
;
2
1
13. Схема Холецького
Метод Холецького використовується для розв’язуванняСЛАР з симетричними матрицями ( aij a ji , i, j 1, n).
a11
a
21
a31
...
an1
a12
a22
a32
...
an 2
... a1n l11
... a2 n l21
... a3 n l31
... ... ...
... ann ln1
0
0
...
l22
l32
0
l33
...
...
...
...
...
ln 2
ln 3
...
0 u11
0 0
0 0
... ...
lnn 0
Самостійно: розглянути метод Холецького.
u12
...
u22
0
u23
u33
...
...
0
0
... u1,n
... u2,n
... u3,n
... ...
... un ,n
14.
Обчислення det(A) та розв’язування СЛАРI.
Обчислення det(A) на основі LU-розкладу матриці
det(A)= det(LU)= det(L) det(U) = l11l22 ...ln ,n .
II.
Розв’язування СЛАР на основі LU-розкладу
матриці
1. Розкладання матриці A = LU
2. Розв’язування системи Ly = b
3. Розв’язування системи Ux = y
15.
Обернена матриця це матриця, для якоїAA-1 = E
a11
a
21
a31
an1
a12
a22
a32
an 2
a1n z11
a2 n z21
a3n z31
ann zn1
z12
z22
z32
zn 2
.
.
.
z1, n 1
z2, n 1
z3, n 1
. zn ,n 1
z1, n 1
z2, n 0
z3, n 0
.
znn 0
0
1
0
.
0
0
1
.
0
1
0
0
0
Для обчислення оберненої матриці необхідно розв’язати n систем
лінійних алгебраїчних рівнянь виду:
A Z(j)= (j), j=1,n
де
Z(j) j-й стовпчик оберненої матриці,
(j) j-й стовпчик одиничної матриці.
0
0
0
.
1
16. Обчислення A-1
Знаючи розкладобчислити як
A LU,
обернену матрицю легко
A 1 U 1L 1 .
i 1
1
lij
(L )
1
uij
(U )
ij lik kkj
k j
lii
ij
, i j , ..., n,
j
uik kkj
k i 1
uii
, i j , ..., 1.
17. РОЗВ’ЯЗУВАННЯ ПЕРЕВИЗНАЧЕНИХ СИСТЕМ РІВНЯНЬ
Припустимо, що системаAx = b
має матрицю A розмірністю m n (m > n).
Така система має безліч розв’язків, але можна
вибрати серед них таке, що мінімізує нев’язку
розв’язку = b – Ax.
Початкова перевизначена система зводиться до
так званої нормальної форми
(ATA)x = Cx = ATb
Звідки
x = (ATA)-1ATb
Матриця С = ATA розмірністю (n n) неособлива,
якщо стовпці матриці A незалежні.
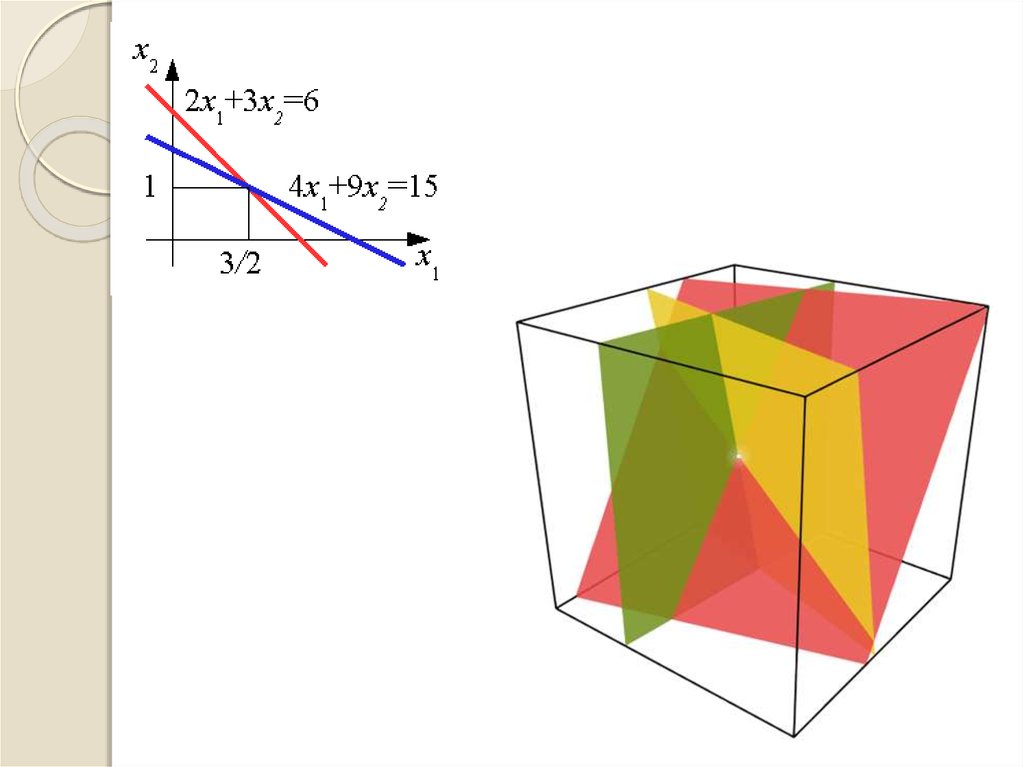
18. ТОЧНІСТЬ РОЗВ’ЯЗКУ СЛАР
6,1 x 1 + 3,4 x 2 = 6,114,7 x 1 + 8,2 x 2 = 14,7
x 1= 1; x 2 = 0.
6,1 x 1 + 3,4 x 2 = 6,101
14,7 x 1 + 8,2 x 2 = 14,7
x 1= 1,205; x 2 = -0,3675.
6,101 x 1 + 3,4 x 2 = 6,1
14,7 x 1 + 8,2 x 2 = 14,7
x 1= 0,829875; x 2 = 0,304979.
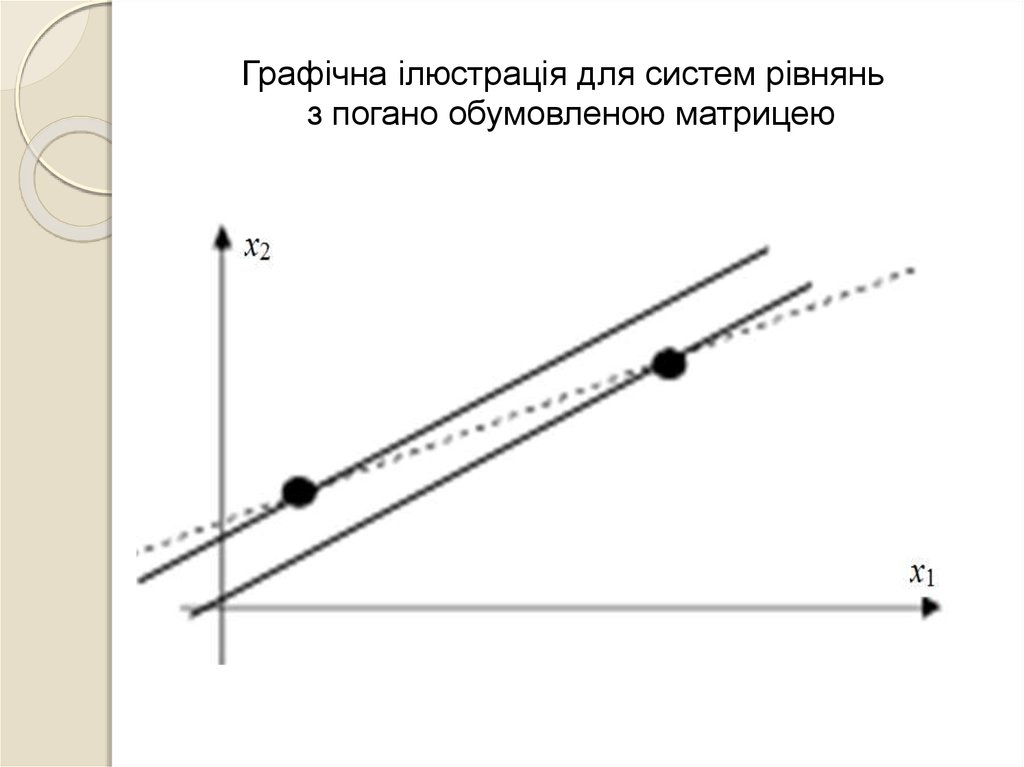
19.
Графічна ілюстрація для систем рівняньз погано обумовленою матрицею
20. Норми векторів
Норма lp||x|| p = (|x 1 | p + |x 2 | p +…+|x n | p ) 1/p
Евклидова норма
= (|x 1 | 2 + |x 2 | 2 +…+|x n | 2 ) 1/2
||x|| 2
Норма l1
= (|x 1 | + |x 2 | +…+|x n |)
||x|| 1
Норма l
||x|| = max
{|x 1 |,|x 2 |,…,|x n |)
i
n
p
| xi |
i 1
p
21. Норми матриць
Норма lp|| A || p
n
p
n
| aij |
p
i 1 j 1
Евклидова норма
|| A ||E
Норма l1
Норма l
n
n
| aij
i 1 j 1
n
|| A ||1 max | aij
j
i 1
| , j 1, n
n
|| A || max | aij
i
j 1
| , i 1, n
2
|
22. ВЛАСТИВОСТІ НОРМ
векторів:||x|| ≥ 0
||x|| = 0 лише для x = 0
|| c x|| = |c| ||x|| для всіх комплексних чисел c
||x + y|| ≤ ||x|| + ||y||
матриць:
||A|| ≥ 0
||A|| = 0 лише для A=0
|| c A|| = | c | ||A|| для всіх комплексних чисел c
||A + B|| ≤ ||A|| + ||B||
||AB|| ≤ ||A|| ||B||
23. ЧИСЛО ОБУМОВЛЕНОСТІ
Нехай x* − точний розв’язок,xн − обчислене (наближене) значення розв’язку,
δx = (x* − xн) − похибка розв’язку.
= b − A xн − нев’язка розв’язку системи A x* = b.
Розглянемо випадок, коли
A(x* + δx) = b + δb,
звідки
δx = A-1δb.
Користуючись нормами , запишемо:
||δx|| ≤ ||A-1|| ||δb||,
||b|| ≤ ||A|| || x* ||
||δx|| ||b|| ≤ ||A-1|| ||δb|| ||A|| || x* ||.
||δx||
|| x* ||
≤ ||A|| ||A-1||
||δb||
||b||
24. ЧИСЛО ОБУМОВЛЕНОСТІ
Припустимо, що (A + δA)(x* + δx) = b.Маємо
A δx + δA(x* + δx) = 0
− δx = A-1δA(x* + δx),
||δx|| ≤ ||A-1|| ||δA|| ||(x* + δx)||.
Звідки
||δx||
≤ ||A|| ||A-1||
|| x* + δx||
||δA||
||A||
Число обумовленості cond (A) =
||A|| ||A-1||
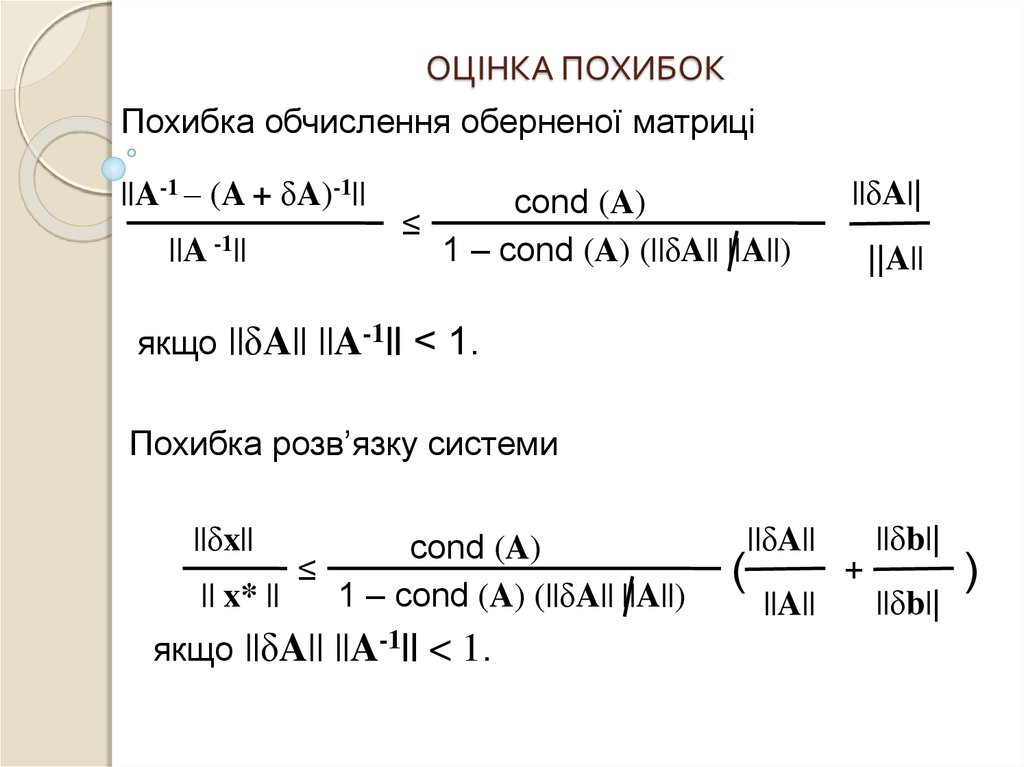
25. ОЦІНКА ПОХИБОК
Похибка обчислення оберненої матриці||A-1 – (A + δA)-1||
||A -1||
cond (A)
≤
1 – cond (A) (||δA|| ||A||)
||δA||
||A||
якщо ||δA|| ||A-1|| < 1.
Похибка розв’язку системи
||δx||
cond (A)
≤
|| x* ||
1 – cond (A) (||δA|| ||A||)
якщо ||δA|| ||A-1|| < 1.
(
||δA||
||A||
||δb||
+
||δb||
)
26. ТОЧНІСТЬ РОЗВ’ЯЗКУ СЛАР
6,1 x 1 + 3,4 x 2 = 6,114,7 x 1 + 8,2 x 2 = 14,7
x 1= 1; x 2 = 0.
6,1 x 1 + 3,4 x 2 = 6,101
14,7 x 1 + 8,2 x 2 = 14,7
x1= 1,205; x 2 = -0,3675.
6,101 x 1 + 3,4 x 2 = 6,1
14,7 x 1 + 8,2 x 2 = 14,7
x 1= 0,829875; x 2 = 0,304979.
cond(A)=1.1908*104
|A| = 0.04























 mathematics
mathematics








