Визначники матриць (продовження). Системи лінійних рівнянь

1.

Лекція №2.
Тема Визначники матриць (продовження)
Системи лінійних рівнянь.
План
1. Властивості визначників.
2. Правило обчислення визначника n- го порядку
3. Розв’язування систем n лінійних рівнянь з n
невідомими Формули Крамера.
4. Обернена матриця.
5. Розв’язування систем n лінійних рівнянь з n
невідомими за допомогою оберненої матриці.

2.

Властивості визначників
Властивість 1.
Значення визначника не змінюється при
транспонуванні.
Приклад 1.
Наслідок. У визначнику рядки та стовпці мають
однакові властивості.
Властивість 2.
Визначник змінить знак на протилежний, якщо
поміняти місцями будь-які два рядки.
Приклад 2.

3.

Властивості визначників
Властивість 3.
Визначник, стовпець якого складається з нулів,
дорівнює нулеві.
Приклад 3
Властивість 4.
Визначник, що має два однакових стовпця,
дорівнює нулеві.
Приклад 4

4.

Властивості визначників
Властивість 5.
Визначник, що має два пропорційні стовпці,
дорівнює нулю.
Приклад 5
Властивість 6.
Визначник зросте у k раз, якщо усі елементи
одного стовпця (рядка) помножити на однакове
число k.
Наслідок. Спільний множник елементів одного стовпця можна винести за
знак визначника.
Приклад 6

5.

Властивості визначників
Властивість 7.
Значення визначника не зміниться, якщо до
елементів якогось стовпця додати (відняти)
відповідні елементи іншого стовпця, що
помножені на одне і те ж число.
Приклад 7
1 рядок ×(-4) +2 рядок; 1 рядок ×(-7) +3 рядок

6.

Властивості визначників
Властивість 8.
Якщо у визначнику елементи i-го рядка є
сумою двох доданків, то він дорівнює сумі двох
відповідних визначників.
Приклад 8

7.

Правило обчислення визначника n- го
порядку.
Для обчислення визначників порядку
використовують алгебраїчні доповнення
Мінори та алгебраїчні доповнення елементів
визначника
Мінором
елемента
називається
визначник (n-1)-го порядку, утворений з визначника
n- го порядку, викресленням i-го рядка та j- го
стовпця.
Алгебраїчним доповненням
елемента
визначника називається мінор цього елемента взятий
з відповідним знаком.

8.

Правило обчислення визначника n- го
порядку.
Приклад 9
Знайти алгебраїчні доповнення елементів a21 та a33
визначника
Розв’язок

9.

Правило обчислення визначника n- го
порядку.
Приклад 10
Записати алгебраічне доповненя елемента a23
визначника
Розв’язок
А23 = 313

10.

Правило. Розклад визначника за елементами
рядка (стовпця).
(теорема Лапласа (23.03.1747-5.03.1827)).
Визначник n-го порядку дорівнює сумі добутків усіх
елементів будь-якого стовпця (або рядка ) на
відповідні їм алгебраїчні доповнення.
У випадку використання i-го рядка правило має вигляд

11.

Обчислення визначника порядку n≥3 .
Приклад 11

12.

Обернена матриця.
Матрицю А-1 називають оберненою до матриці А,
якщо виконуються рівності
А× А-1 = А-1×А =Е.
Умови існування А-1 до А:
1) А - квадратна;
2) ∆ А≠ 0.
Обернена матриця має вигляд
де Аij = (-1)i+j Mij – алгебраїчні доповнення елемента aij.

13.

A
Обернена матриця.
Приклад 12
Знайти матрицю, обернену до матриці
Розв’язок
1) Обчислюємо значення визначника матриці А
2) Знаходимо алгебраїчні доповнення усіх елементів

14.

Приклад 12 (продовження)
3) Записуємо обернену до А матрицю

15.

Системи лінійних рівнянь
Систему алгебраїчних рівнянь називають лінійною,
якщо вона може бути записана у вигляді
де x1, x2, … , xn, - невідомі; aij - коефіцієнти системи;
bk - вільні члени.

16.

Системи лінійних рівнянь
Розв’язком системи називають множину дійсних чисел
с1, с2, …, сn, підстановка яких у систему замість
невідомих, перетворює кожне рівняння у тотожність.
Систему лінійних рівнянь (С. Л. Р.) називають
сумісною якщо вона має хоч би один розв’язок,
несумісною в протилежному випадку.
системи лінійних рівнянь
сумісні
несумісні
Визначені
Невизначені
мають єдиний мають безліч
розв’язок
розв’язків
не мають жодного
розв’язку

17.

Системи лінійних рівнянь
Знаходження єдиного розв’язку
Системи n лінійних рівнянь з n невідомими .
С. Л. Р. має єдиний розв’язок, якщо визначник
матриці з коефіцієнтів цієї системи не дорівнює
нулю

18.

Системи n лінійних рівнянь з n невідомими
Метод Крамера.
Розв’язком С.Л.Р. за правилом Крамера буде
сукупність значень невідомих обчислених за
формулами:
1
2
n
x1 , x2 , , xn ,
де
j
a11
a12
a21
a22
a2, j 1b2 a2, j 1 a2 n
a1, j 1b1a1, j 1
a1n
, j 1, n
an1 an 2 an , j 1bn a2, j 1 ann
Цей визначник отримано шляхом послідовної заміни j-го стовпця
визначника ∆ стовпцем чисел b1 , b2 , … , bn .

19.

Приклад 13
Розв’язати систему лінійних рівнянь за формулами
Крамера:
x1 2 x2 x3 1,
2 x1 x2 x3 5,
3 x 2 x 6 .
1
2
Розв’язок
1 2
2
1
1
1 2 1
1 3 1 0 1 1
1 3
3 2
0
3 2 0
3 1
3 2
6 3 3.
∆ ≠ 0, можемо застосувати правило Крамера
1 2
1
1 2 1
6 1
1 5 1 1 6 1 0 1 1 1 3
6 2 1 6 6.
6 2
6 2 0 6 2 0

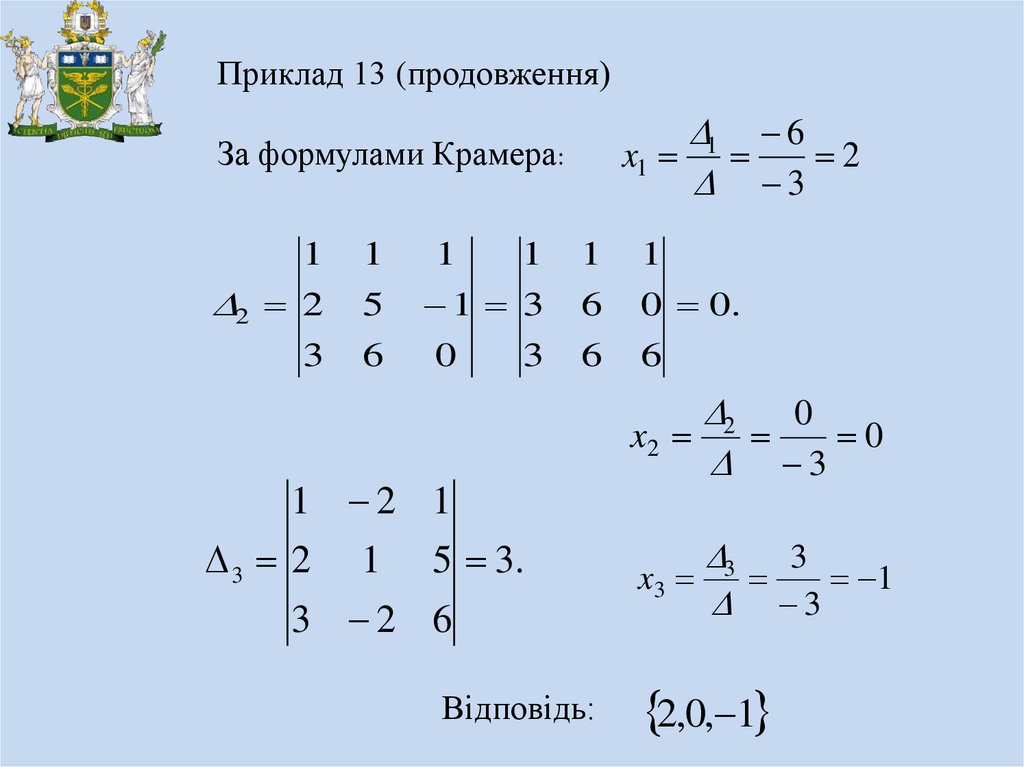
20.

Приклад 13 (продовження)
1 6
x1
2
3
За формулами Крамера:
1
1
2 2
5
3
6
1
1
1
1
1 3
6
0 0.
6
6
0
3
1 2 1
3 2
1
5 3.
3 2 6
Відповідь:
2
0
x2
0
3
3
3
x3
1
3
2,0, 1

21.

Системи n лінійних рівнянь з n невідомими
Метод оберненої матриці.
то С.Л. Р. , згідно з правилом множення матриць та
умовою рівності матриць, можна записати у матричній
формі
A×X = B
Тоді
A-1∙A×X = A-1∙ B ( A-1∙A =E)
X= A-1∙ B
де A-1 - матриця обернена до A.

22.

Приклад 14
Розв’язати C.Л.Р. методом оберненої матриці
x1 2 x2 x3 1,
2 x1 x2 x3 5,
3 x 2 x 6 .
1
2
Розв’язок
Запишемо систему рівнянь у вигляді матричного
рівняння A X B
де
Тоді
1 2 1
A 2 1 1 ,
3 2 0
1
X A
B
x1
1
X x2 , B 5 .
x
6
3

23.

Приклад 14 (продовження)
1 2
A 2
1
1
1 3 0
3 2 0
Знаходимо алгебраїчні доповнення:
A11 1
1 1
A13 1
1 3
A22 1
2 2
1
1
2
0
2
1
3
2
1 1
3 0
2;
7;
3;
2 1
A12 1
A21 1
2 1
1 2
2 1
A23 1
2 3
3
0
2 0
1 2
3 2
3;
2;
4;

24.

Приклад 14 (продовження)
A31 1
3 1
A33 1
3 3
2
1
1
1
1 2
2
1
1;
A32 1
3 2
5.
Запишемо обернену матрицю до матриці А
A11 A21 A31
2 2 1
1
1
1
A A12 A22 A32 3 3 3
A
3
A
A
A
7
4
5
23
33
13
1
1
2 1
3;

25.

Приклад 14 (продовження)
2 2 1 1
2 1 2 5 1 6
1
1
1
X A B 3 3 3 5 3 1 3 5 3 6
3
3
7 4 5 6
7 1 4 5 5 6
6 2
1
0 0
3
3 1
Відповідь:
2,0, 1