Задача лінійного програмування та деякі методи їх розв’язування

1. Черкаський державний технологічний університет

ТЕМА: “Задача лінійного
програмування та деякі методи їх
розв’язування"
Дисципліна
“Інформаційні технології
аналізу систем”
Лекція 8-9
Викладач: Герасименко І. В.
© проф. Триус Ю.В.

2. Питання:

1. Загальна задача лiнiйного програмування та її
подання в канонічній формі.
2. Поняття плану, опорного плану,
невиродженого опорного плану, оптимального
плану задачі лінійного програмування.
3. Властивості розв’язків задачі лінійного
програмування.
4. Геометричний метод розв’язування задачі
лінійного програмування.

3. 1. Загальна задача лiнiйного програмування та її подання в канонічній формі

Задача однокритеріальної оптимізації
f ( x) min(max) , x X ,
в якій цільова функція лiнiйна i множина X
визначається системою лiнiйних рiвнянь i(або)
нерiвностей називається задачею лiнiйного
програмування.

4. 1. Загальна задача лiнiйного програмування та її подання в канонічній формі

Загальна задача
лінійного програмування
n
f ( x) c j x j min(max)
j 1
n
X {x R n | aij x j bi , i 1, k ,
j 1
n
aij x j bi , i k 1, m,
j 1
x j 0, j 1, s, s n}
де c j , aij , bi R1 i 1, m, j 1, n - задані дійсні числа.
(1)

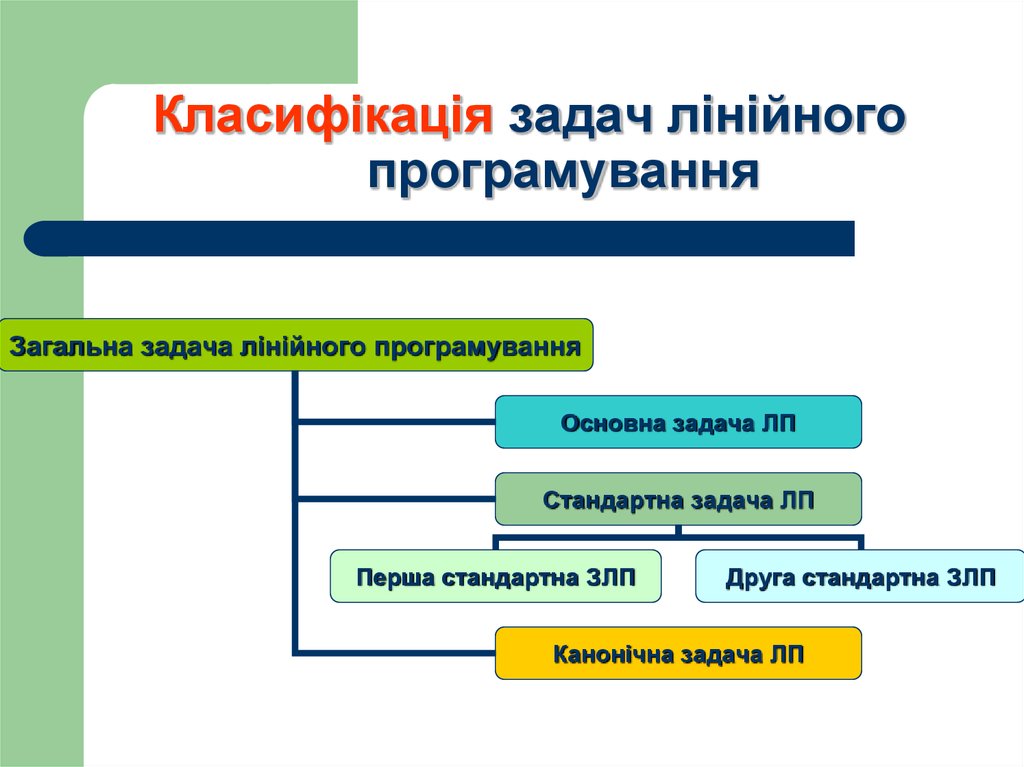
5. Класифікація задач лінійного програмування

Загальна задача лінійного програмування
Основна задача ЛП
Стандартна задача ЛП
Перша стандартна ЗЛП
Друга стандартна ЗЛП
Канонічна задача ЛП

6. 1. Загальна задача лiнiйного програмування та її подання в канонічній формі

Основна задача лінійного програмування
n
f ( x) c j x j min(max) ,
j 1
(2)
n
X {x R | aij x j bi , i 1, m},
n
j 1
де c j , aij , bi R1 i 1, m, j 1, n - задані дійсні числа.

7. 1. Загальна задача лiнiйного програмування та її подання в канонічній формі

Перша стандартна задача лінійного
програмування
n
f ( x) c j x j max ,
j 1
n
(3)
X {x R n | aij x j bi ,i 1, m, x j 0, j 1, n},
j 1
де c j , aij , bi R1 i 1, m, j 1, n - задані дійсні числа.

8. 1. Загальна задача лiнiйного програмування та її подання в канонічній формі

Друга стандартна задача лінійного
програмування
n
f ( x) c j x j min ,
j 1
n
(3’)
X {x R n | aij x j bi ,i 1, m, x j 0, j 1, n},
j 1
де c j , aij , bi R1 i 1, m, j 1, n - задані дійсні числа.

9. 1. Загальна задача лiнiйного програмування та її подання в канонічній формі

Канонічна задача лінійного програмування
n
f ( x) c j x j min(max)
j 1
n
(4)
X {x R n | aij x j bi ,i 1, m, x j 0, j 1, n},
j 1
де c j , aij , bi R1 i 1, m, j 1, n - задані дійсні числа.

10. Економічна постановка задачі

Приклад 1.
Економічна постановка задачі
Підприємство може здійснювати випуск продукції
за трьома технологіями Т1, Т2 ,Т3. Види і норми
витрат ресурсiв на один виріб продукції,
продуктивність кожної технології та загальна
кiлькiсть наявних ресурсiв наведено в таблицi.
Визначити скiльки часу необхiдно працювати за
кожною з технологій, щоб обсяг виробництва
підприємством продукції за наявних умов був
найбільшим.

11. Таблиця вхідних даних

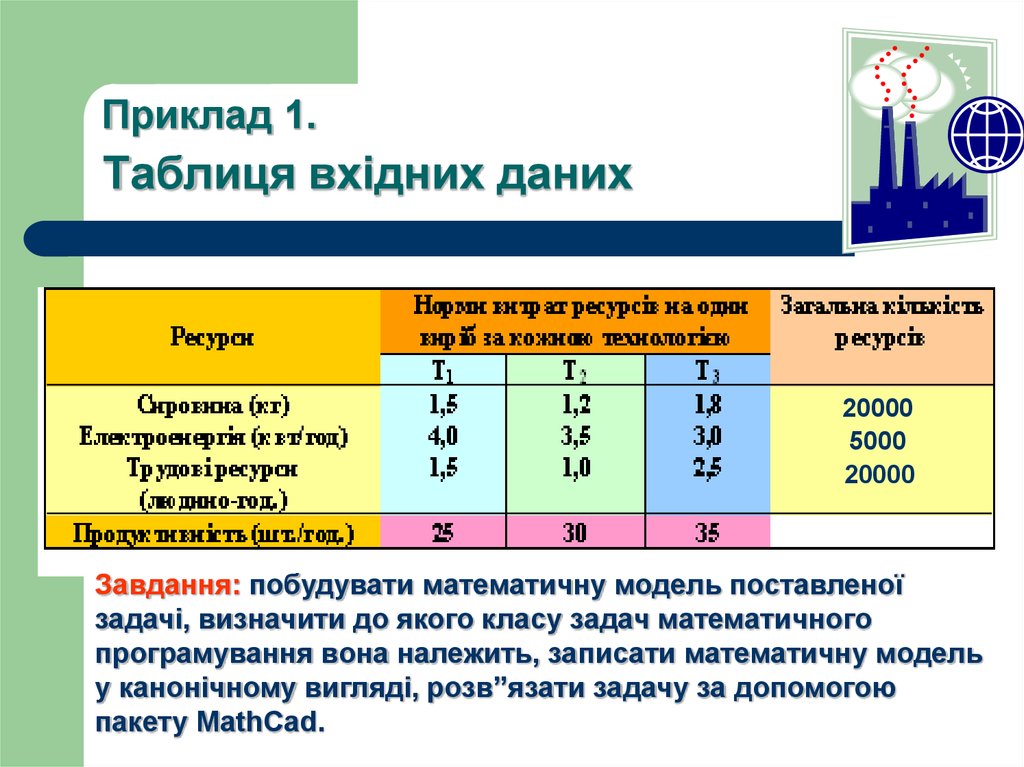
Приклад 1.
Таблиця вхідних даних
20000
5000
20000
Завдання: побудувати математичну модель поставленої
задачі, визначити до якого класу задач математичного
програмування вона належить, записати математичну модель
у канонічному вигляді, розв”язати задачу за допомогою
пакету MathCad.

12. Математична модель задачі з прикладу 1

F ( x1 , x2 , x3 ) 25 x1 30 x2 35 x3 max
1,5 25 x1 1,2 30 x2 1,8 35 x3 20000,
4 25 x1 3,5 30 x2 3 35 x3 5000,
1,5 25 x 1 30 x 2,5 35 x 20000,
1
2
3
x j 0, j 1,3,
де
xi
– кількість годин роботи за Тi-ою технологією (i=1,2,3).

13. Канонічна форма математичної моделі задачі з прикладу 1

F ( x) 25 x1 30 x2 35 x3 0 x4 0 x5 0 x6 max
1,5 25 x1 1,2 30 x2 1,8 35 x3 x4 20000,
4 25 x1 3,5 30 x2 3 35 x3 x5 5000,
1,5 25 x 1 30 x 2,5 35 x x 20000,
1
2
3
6
x j 0, j 1,6

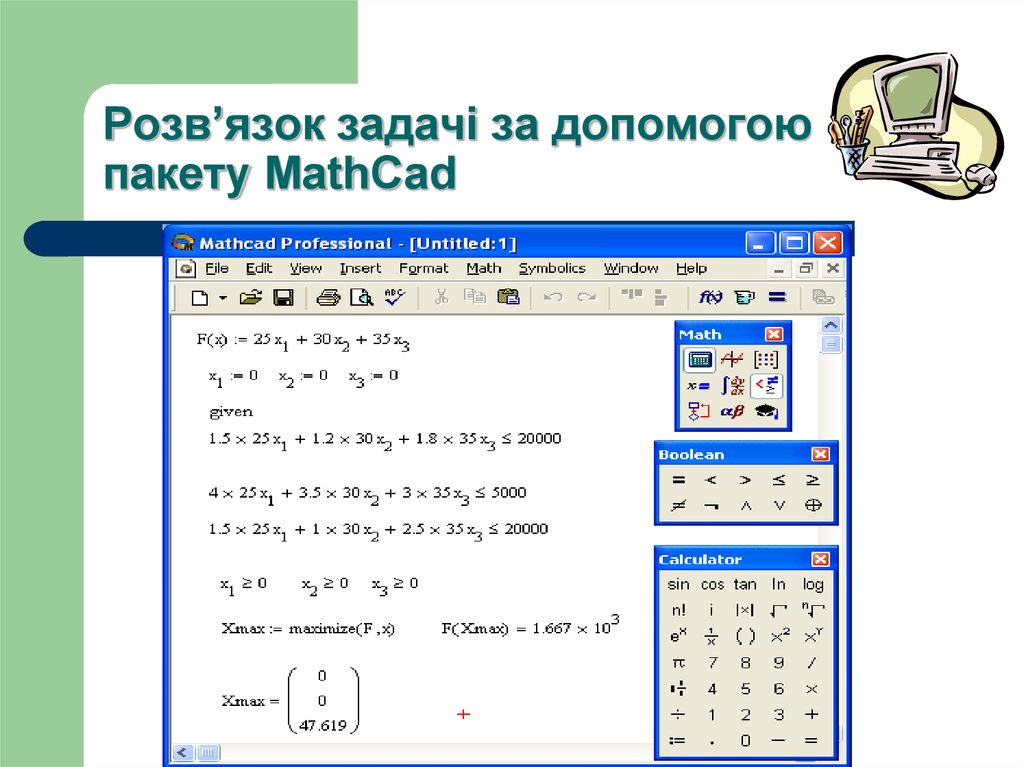
14. Розв’язок задачі за допомогою пакету MathCad

15. Висновок:

Оптимальний план використання
технологій для випуску продукції:
підприємством
за технологією Т1 – 0 годин,
за технологією Т2 – 0 годин,
за технологією Т3 – 47,6 години.
При цьому максимальний обсяг випуску продукції
підприємством становить
1666 виробів.

16. 2. Поняття плану, опорного плану, невиродженого опорного плану, оптимального плану задачі лінійного програмування

Розглянемо задачу лінійного програмування,
записану в канонічній формі:
(5)
(6)
(7)
f ( x) c1 x1 c2 x2 ... cn xn min (max) ,
a11 x1 a12 x 2 ... a1n x n b1 ,
a x a x ... a x b ,
21 1
22 2
2n n
2
...........................................
a m1 x1 a m 2 x 2 ... a mn x n bm ,
x j 0 , j 1, n
bi 0 , i 1, m , m n

17. 2. Поняття плану, опорного плану, невиродженого опорного плану, оптимального плану задачі лінійного програмування

Введемо позначення:
c (c1 , c2 ,..., cn ) X ( x1 , x2 ,..., xn )
a12
a1n
a11
a1m
b1
a
1
m
1
a
22
a 21
a2m
a2n
b2
a 2 m 1
,
,
,
P
2
P1
P
,
,
.....,
m
.
Pn P0 .
. P m 1
.
.
.
.
a
a
a
m1
m2
mm
a mm 1
b
m
a
mn
f ( x) c, X min (max)
x1 P1 x2 P2 ... xm Pm ... xn Pn P0
X 0

18. 2. Поняття плану, опорного плану, невиродженого опорного плану, оптимального плану задачі лінійного програмування

Означення 1. Планом задачі лінійного
X ( x1 , x2 ,..., xn ) ,
програмування (5)-(7) називається вектор
компоненти якого задовольняють умови (6), (7).
Означення 2. План X ( x1 , x2 ,..., xn ) задачі (5)-(7)
Pj
називається опорним, якщо вектори
, які відповідають
додатним компонентамx j плану Х, утворюють
лінійно-незалежну систему.
Зауваження. Оскільки векториP j є m-вимірними, то максимальне
число таких векторів, що утворюють лінійно-незалежну систему,
не перевершує m. Звідси випливає, що кожний опорний план
містить не більше ніж m додатних компонент.

19. 2. Поняття плану, опорного плану, невиродженого опорного плану, оптимального плану задачі лінійного програмування

Означення 3. Опорний план називається невиродженим,
якщо він містить рівно m додатних компонент. Якщо
опорний план містить менше за m додатних компонент, то
такий опорний план називається виродженим.
Означення 4. Оптимальним планом або розв`язком
задачі лінійного програмування (5)-(7), називається план
цієї задачі, який мінімізує (максимізує) лінійну функцію
(5), іншими словами, Х* – оптимальний план задачі
лінійного програмування, якщо для будь-якого плану Х
задачі (5)-(7) виконується умова f ( X *) f ( X ) f ( X * f ( X )

20. 2. Поняття плану, опорного плану, невиродженого опорного плану, оптимального плану задачі лінійного програмування

Приклад 2. Нехай задача лінійного програмування має вигляд
f(x)=2x1–х2+2x3–3x4 min;
3x1 2 x2 x3 5 x4 2,
x1 3x2 2 x3 3x4 3;
xj 0, j=1, 2, 3, 4.
З”ясувати, які з векторів є планами, опорними планами:
Х1=(1,0,1,0) Х2=(0,1,0,1) Х3=(0,1,0,0)
3
1
Х4=(0,0,3,1) X 5 ,0,0, X 6 1 ,0,2, 1
2
2
2
2

21. 3. Властивості розв’язків задачі лінійного програмування

3. Властивості розв’язків задачі
лінійного програмування
Запишемо задачу (5) – (7) у матричному
вигляді:
T
(8)
f ( X ) cX min(max)
T
(9)
A X b
(10)
X 0
a11 a12 ...a1n
b
1
a a ...a
b b2 A 21 22 2 n
...
......
a
a
.
.
.
a
bm
m1 m 2 mn

22. 3. Властивості розв’язків задачі лінійного програмування

3. Властивості розв’язків задачі
лінійного програмування
Теорема 1. Множина всіх планів задачі
(8)–(10) – опукла.
Опуклу множину планів задачі лінійного
програмування позначимо через М.
Зауважимо, що М може бути порожньою
множиною, опуклим многогранником або
необмеженою опуклою многогранною
областю.

23. 3. Властивості розв’язків задачі лінійного програмування

3. Властивості розв’язків задачі
лінійного програмування
Нехай лінійна функція задачі лінійного
програмування обмежена знизу і зверху на множині
планів.
Теорема 2. Лінійна функція задачі лінійного
програмування (8) – (10) досягає мінімального
(максимального) значення у крайній точці опуклої
множини М планів задачі. Якщо лінійна функція
набуває мінімального (максимального) значення
більш ніж в одній крайній точці, то вона набуває
цього ж значення в будь-якій точці, яка є опуклою
комбінацією цих точок.

24. 3. Властивості розв’язків задачі лінійного програмування

3. Властивості розв’язків задачі
лінійного програмування
Теорема 3 (критерій крайності точки
опуклої множини планів). Для того щоб
точка Х, яка містить m додатніх
координат, була крайньою точкою
множини планів М задачі лінійного
програмування (8)-(10), необхідно і досить,
щоб вектори , які відповідають додатним
компонентам , утворювали лінійно
незалежну систему.

25. 4. Геометричний метод розв’язування задачі лінійного програмування

Розглянемо двовимiрну задачу мiнiмiзацiї:
(11) f ( x , x ) min, x X R 2
1
2
Лiнiєю (поверхнею) рiвня функцiї
є множина точок
f (x)
L {x R | f ( x) , R }
n
1

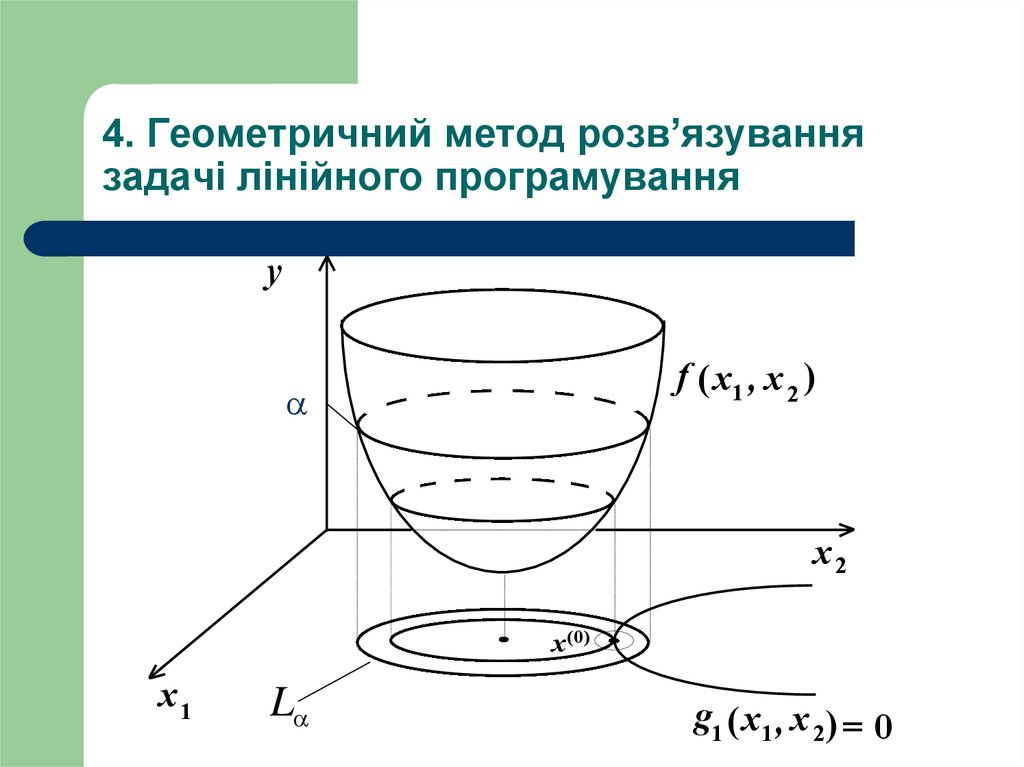
26. 4. Геометричний метод розв’язування задачі лінійного програмування

y
f (x1 , x 2 )
x2
x(0)
x1
L
g1 ( x1 , x 2) = 0

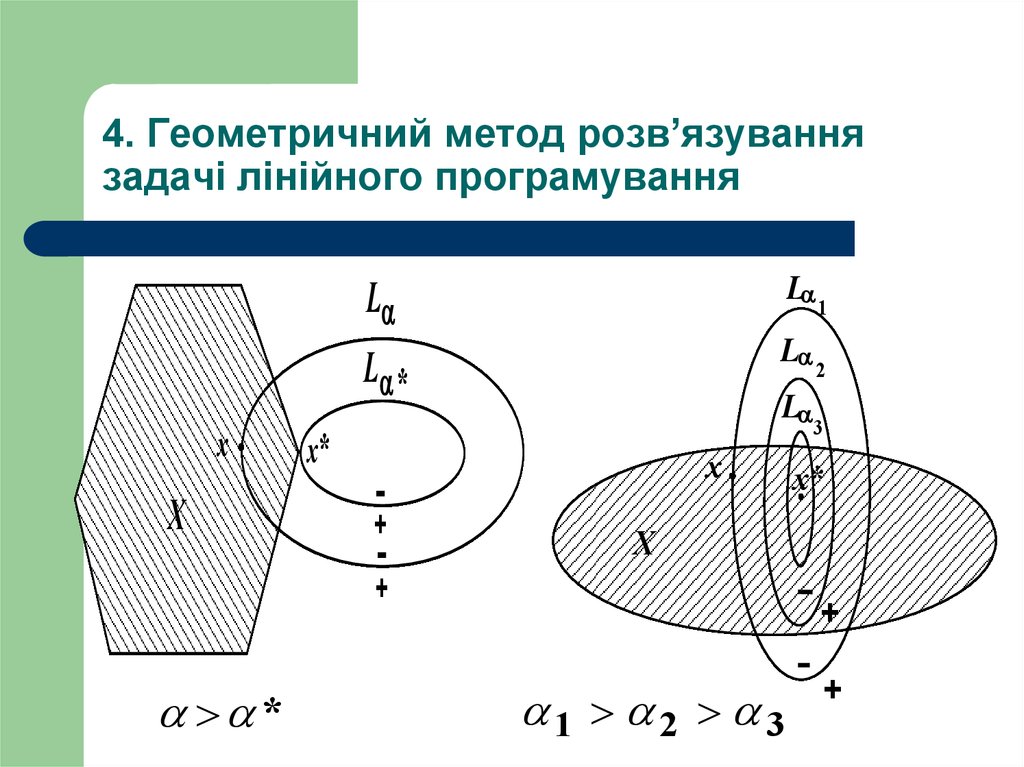
27. 4. Геометричний метод розв’язування задачі лінійного програмування

x
X
L
L 1
L *
L 2
L
x*
x
+
x*
X
+
*
3
+
1 2 3
+

28. 4. Геометричний метод розв’язування задачі лінійного програмування

Особливість геометричної інтерпретації
двовимірної задачі лінійного програмування
f ( x1 , x2 ) с1 x1 c2 x2 min (max) , x X R 2
полягає в тому, що:
- допустима множина X являє собою
опуклу многокутну область (обмежену) або
необмежену;

29. 4. Геометричний метод розв’язування задачі лінійного програмування

лінія рівня цільової функції f ( x1 , x2 ) є пряма, при
цьому градієнт функції - вектор
f f
c
;
x1 x2
(c1 , c2 )
перпендикулярний цій прямій і є напрямом
найшвидшого зростання цільової функції в кожній
точці допустимої множини X, а антиградієнт
(вектор c ) є напрямом її найшвидшого
спадання;
якщо задача має розв’язок, то він досягається
обов’язково на межі допустимої множини X, а сам
розв’язок задачі є або деяка вершина
многокутника або множина точок деякої його
сторони.

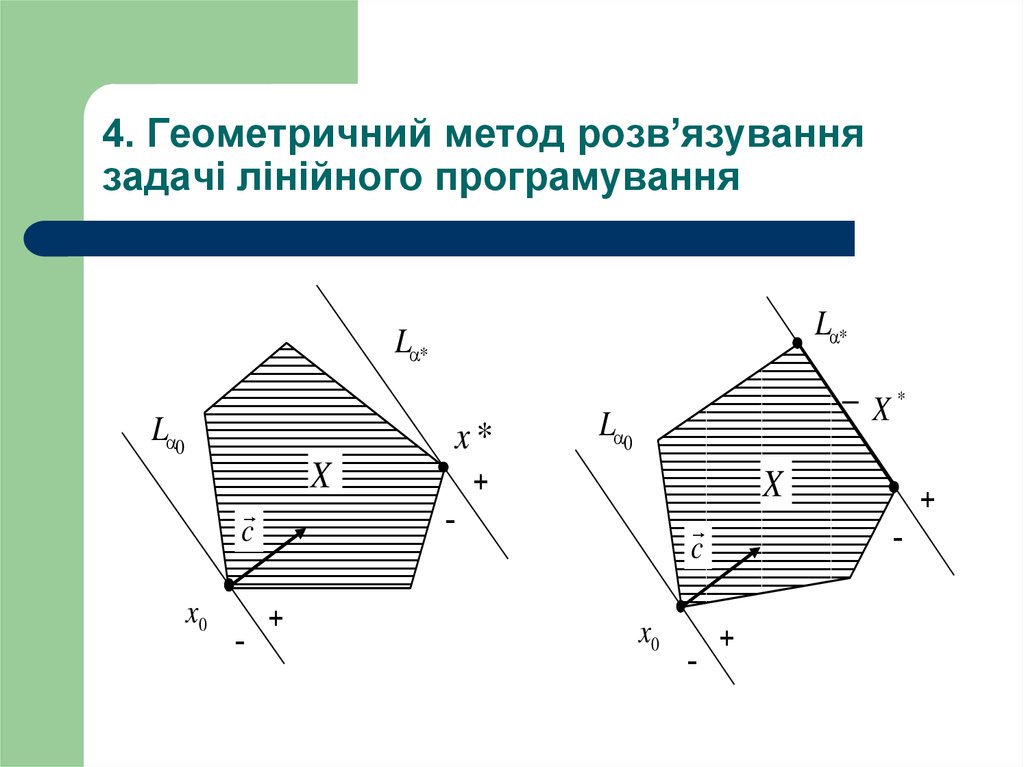
30. 4. Геометричний метод розв’язування задачі лінійного програмування

L *
L *
L 0
x*
X
c
x0
-
X*
L 0
X
+
-
+
c
x0
-
+
-
+

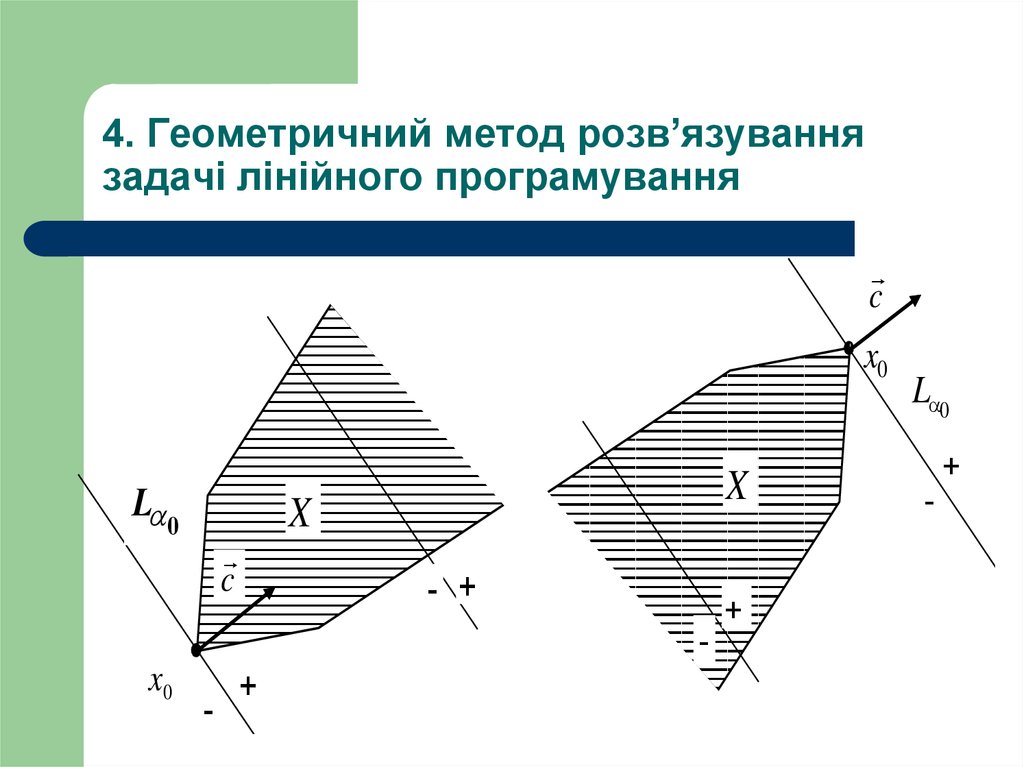
31. 4. Геометричний метод розв’язування задачі лінійного програмування

c
x0
L 0
X
X
c
- +
-
x0
-
+
+
L 0
-
+

32. 4. Геометричний метод розв’язування задачі лінійного програмування

Розглянемо більш детально алгоритм
розв'язування двовимірної задачi лiнiйного
програмування виду:
2
(12)
f ( x) c x min (max)
j 1
j
aij x j bi i 1, m, x j 0, j 1,2
j 1
2
(13)
j

33. 4. Геометричний метод розв’язування задачі лінійного програмування

1. Побудувати прямi, рiвняння яких
одержуються внаслiдок замiни в
обмеженнях (13) знакiв нерiвностей на
знаки рiвностей.
2. Знайти пiвплощини, якi визначаються
кожним з обмежень-нерівностей задачi.
3. Знайти множину допустимих розв”язкiв
задачі M, як перетин знайдених
півплощин.

34. 4. Геометричний метод розв’язування задачі лінійного програмування

4. Побудувати пряму c1 x1 c2 x2 h
(лінію
рівня цільової функції), при цьому величина h
підбирається так, щоб лінія рівня проходила через
множину допустимих розв”язкiв М. Побудувати
вектор c (c1 , c2 ) .
5. Рухаючи пряму c1 x1 c2 x2 h в напрямі
вектора с при розв”язуванні задачі максимізації
(або в зворотньому напрямі при розв”язанні задачі
мінімізації), знайти точку (множину точок), де
цiльова функцiя приймає максимальне (мiнiмальне)
значення, або встановити необмеженiсть зверху
(знизу) функцiї на допустимій множинi.

35. 4. Геометричний метод розв’язування задачі лінійного програмування

6. Якщо існує єдиний розв’язок задачі,
визначити координати знайденої точки як
розв’язок системи двох відповідних
рівнянь з двома невідомими, i обчислити
значення цiльової функцiї в цiй точцi.
Якщо існує безліч розв’язків, то визначити
координати принаймні однієї
екстремальної точки i обчислити значення
цiльової функцiї в цiй точцi.

36. 4. Геометричний метод розв’язування задачі лінійного програмування

Приклад 2. На виготовлення двох видів продукції П1 і П2
витрачаються три види ресурсів А1, А2 і А3. Запаси ресурсів,
норми їх витрат і прибуток від реалізації одиниці продукції (у.о.)
задані у таблиці. Знайти такий план виробництва, який би
забезпечував найбільший прибуток.
Побудувати математичну модель поставленої задачі і
розв’язати її геометричним методом.

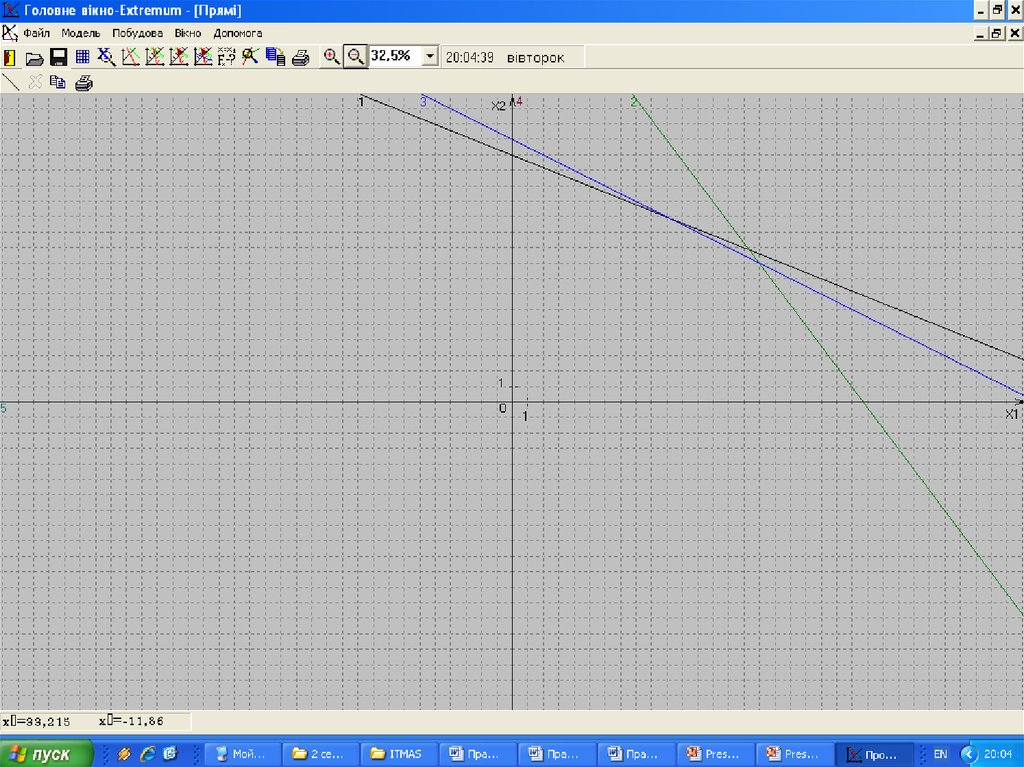
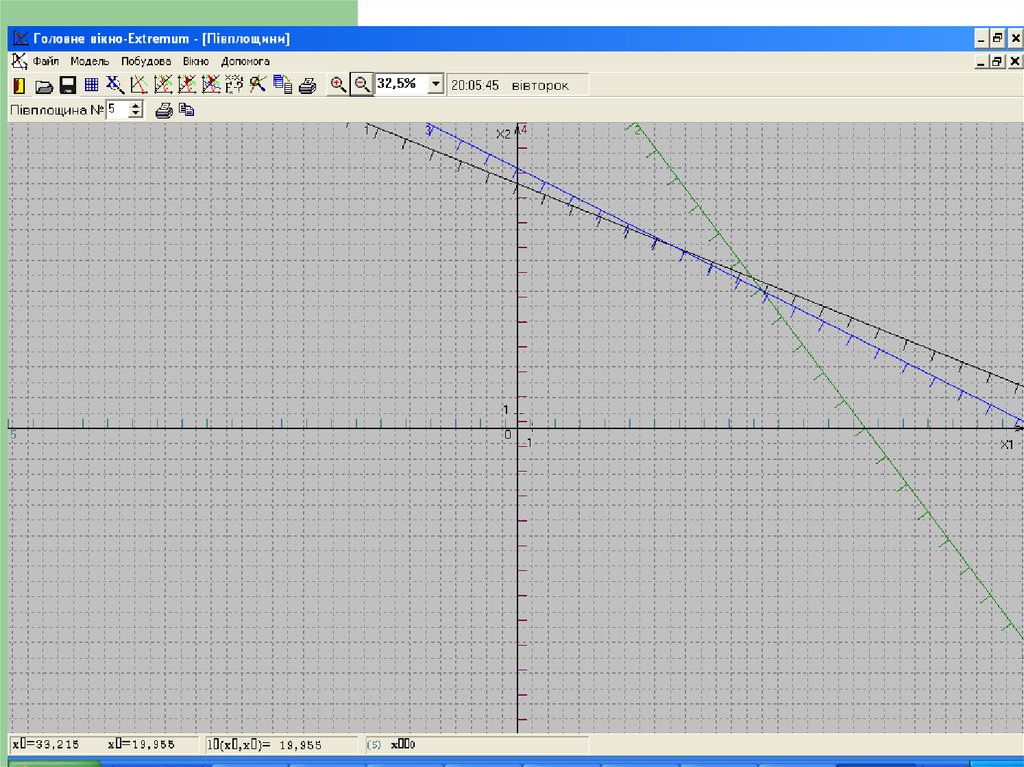
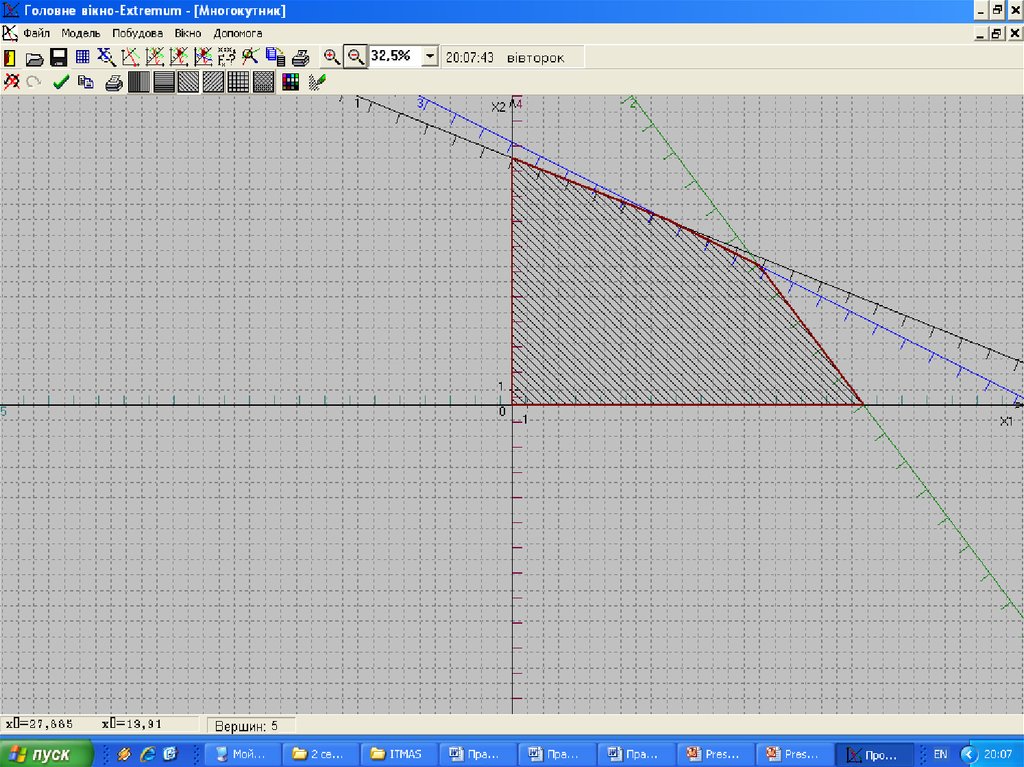
37. 4. Геометричний метод розв’язування задачі лінійного програмування

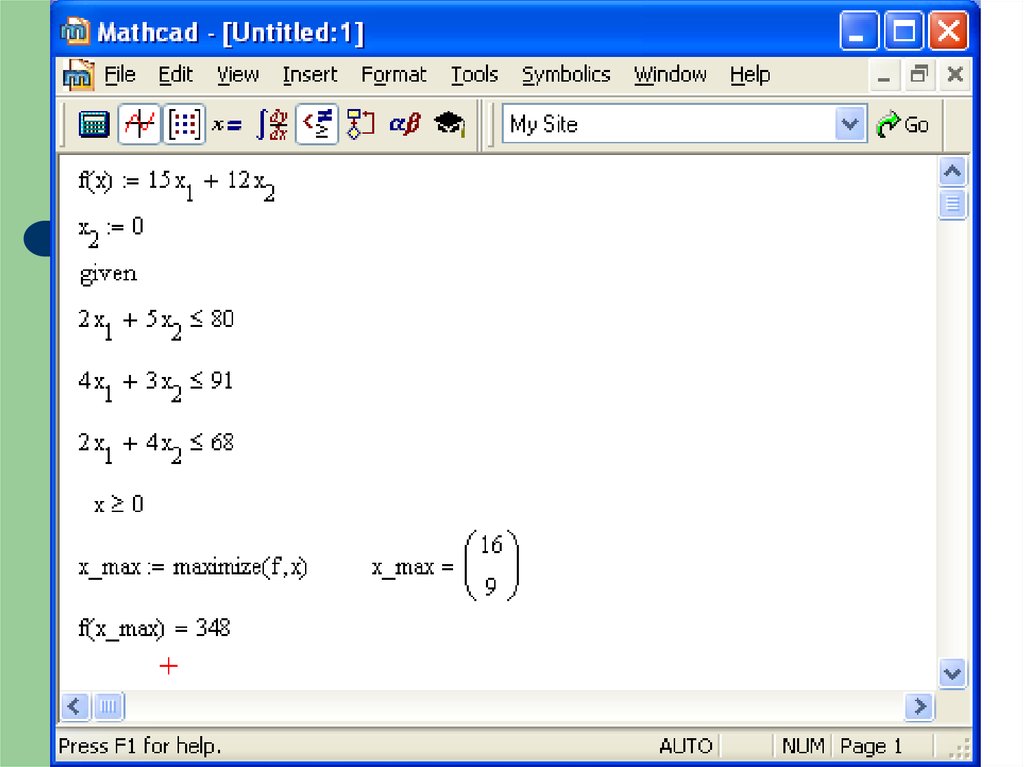
Розв”язування. Математична модель задачі має такий
вигляд:
f ( x) 15x1 12x2 max
2 x1 5 x 2 80,
4 x1 3 x 2 91,
2 x 4 x 68,
2
1
x j 0, j 1,2
де x1 – обсяг випуску
продукції виду П1,
x2 – обсяг випуску
продукції виду П2.

38.

39.

40.

41.

42. 4. Геометричний метод розв’язування задачі лінійного програмування

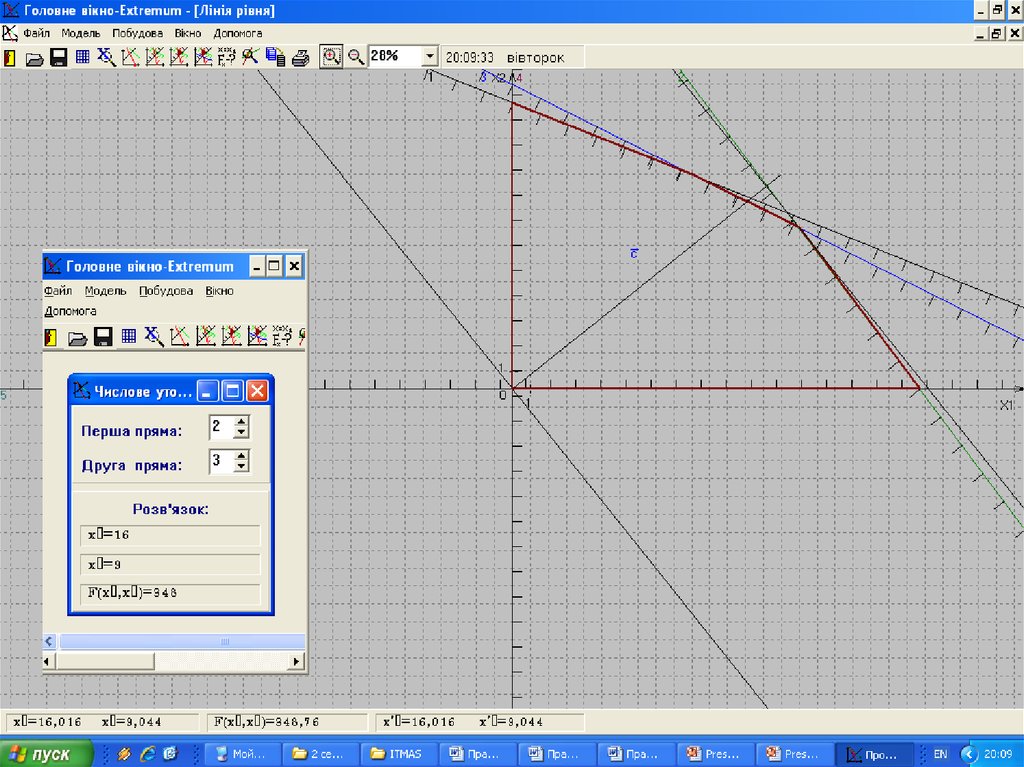
43. 4. Геометричний метод розв’язування задачі лінійного програмування

Відповідь:
Обидва види продукції є рентабельними, при
цьому оптимальний план дорівнює X1*=16,
X2*=9, а оптимальний прибуток від реалізації
продукції дорівнює 348 у.о.

44. Ваші запитання

8(0472) 730271
[email protected]
Дякую за увагу!