Электричество и магнетизм. Лекция 1

1.

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
ЛЕКЦИЯ 1
Электростатика
1

2.

ЭЛЕКТРОСТАТИКА
Савельев И.В. Курс физики: Том 2. Электричество.: Уч.
пособие. Т.1. М.. 4-е изд., стер. – СПб.: Издательство
«Лань», 2011г.-352с:
2. Трофимова Т.И. Курс физики. – М.: Высшая школа,
2002-2009.
6. Калашников С.Г. Электричество. –М.: Физматлит., 2003.
– 480с.
7. Трофимова Т.И. Курс физики. – М.: Высшая школа,
2002-2009.

3.

Взгляды
Электромагнетизм сведен к механическим причинам
Мировой эфир (Фарадей-Максвелл
Поле – как вид материи
Электростатика - раздел учения об электричестве, в котором
изучаются взаимодействия и свойства систем электрических зарядов,
неподвижных относительно выбранной инерциальной системы отсчёта.
Электростатическое поле - частная форма электромагнитного поля,
представляющая собой вид материи, посредством которой
взаимодействуют неподвижные электрические заряды.
Электрический заряд - это скалярная физическая величина,
определяющая интенсивность электромагнитного взаимодействия.
Электрический заряд инвариантен по отношению к различным
системам отсчета. Во всех системах отсчета заряд тела или
частицы имеет одно и то же значение;
- электрический заряд – величина аддитивная. Заряд любой системы
равен сумме зарядов составляющих эту систему тел (частиц).
3

4.

Закон сохранения электрического заряда - суммарный заряд
электрически изолированной системы не может изменяться.
Закон Кулона - сила электрического взаимодействия между
двумя неподвижными заряженными частицами в вакууме
прямо пропорциональна произведению их зарядов и обратно
пропорциональна квадрату расстояния между ними.
q1 q2
F12 k
er
2
r
F12
F21
er
+q1
+q2
er – единичный вектор.
Закон Кулона справедлив при расстояниях от 10-15 м до
нескольких км.
1
k
8, 99 109 9 109
0 = 8,85 10-12 Ф/м
4 0
F12 F21
4

5. Напряженность электрического поля

Электрическим полем называют вид материи, посредством
которой происходит взаимодействие
электрических
зарядов.
Поле, создаваемое неподвижными
электростатическим.
зарядами,
называют
Свойства
электрического
поля:
а)порождается
электрическими
зарядами;
б)обнаруживается по действию на заряд;
в)действует на заряды с некоторой силой.

6.

Напряжённость электростатического поля
Основное свойство электрического поля заключается в том, что на
всякий заряд, помещённый в это поле, действует сила.
Возьмём пробный электрический заряд qпр и поместим его в
электрическое поле, которое создаёт заряд q
er
q
F
r
qпр
F
1 q
e
Величина E
2 r
qпр 4 0 r
не зависит от qпр
и определяется лишь зарядом q, а потому служит
характеристикой поля.
Вектор напряжённости электростатического поля численно равен
силе, действующей в данной точке на помещённый в неё пробный
единичный положительный заряд.
[E]=Н/Кл=В/м
6

7.

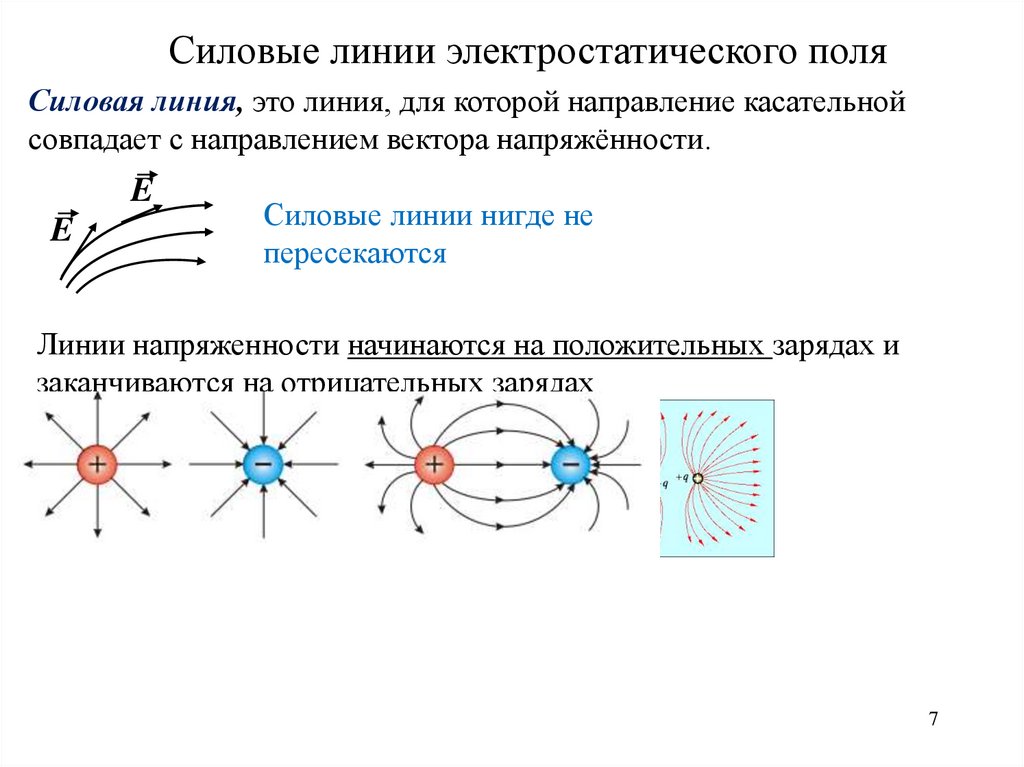
Силовые линии электростатического поля
Силовая линия, это линия, для которой направление касательной
совпадает с направлением вектора напряжённости.
E
E
Силовые линии нигде не
пересекаются
Линии напряженности начинаются на положительных зарядах и
заканчиваются на отрицательных зарядах
7

8.

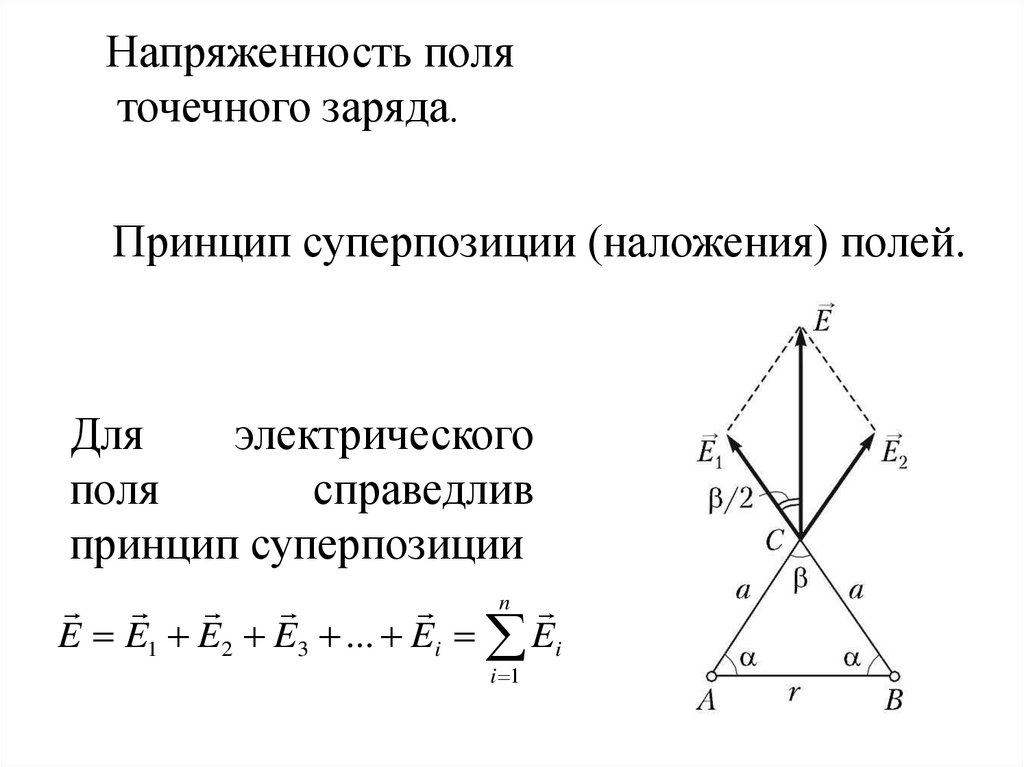
Напряженность поля
точечного заряда.
Принцип суперпозиции (наложения) полей.
Для
электрического
поля
справедлив
принцип суперпозиции
n
E E1 E2 E3 ... Ei Ei
i 1

9.

Свойства электростатического поля
Теорема Гаусса
Теорема о циркуляции напряженности электрического поля Е
ПОТОК
ЦИРКУЛЯЦИЯ
dq – заряд, сосредоточенный на объекте
dq
dV
dq
dS
dq
dl
- объемная плотность заряда
- поверхностная плотность заряда
- линейная плотность заряда,
9

10.

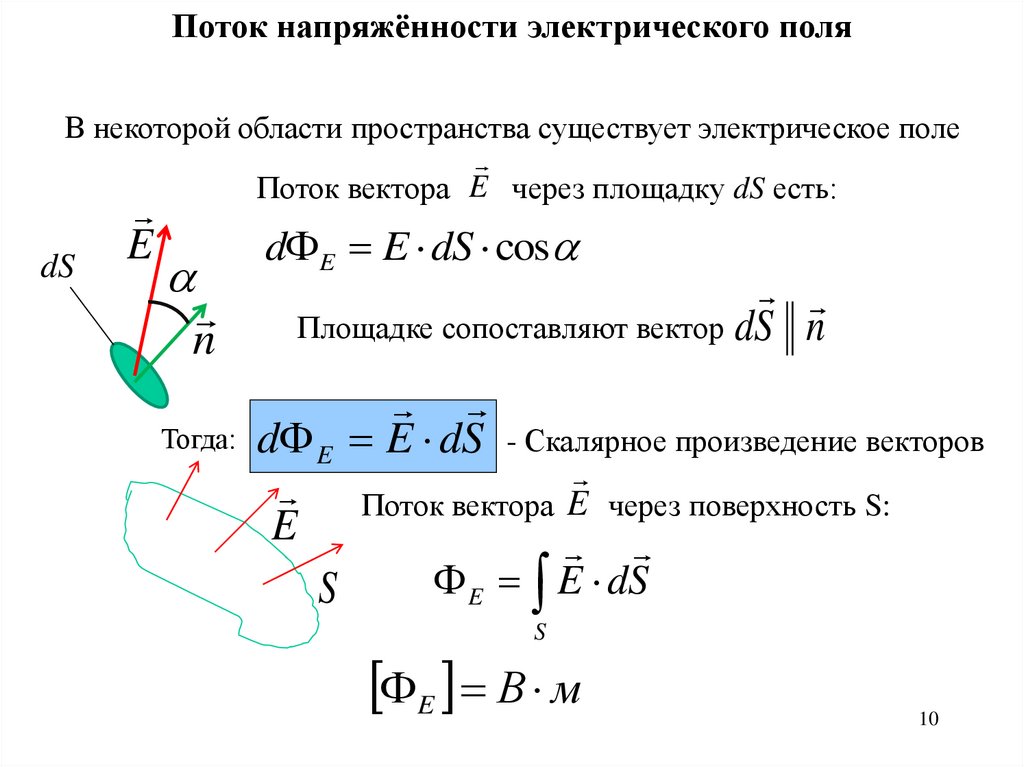
Поток напряжённости электрического поля
В некоторой области пространства существует электрическое поле
Поток вектора E через площадку dS есть:
dS
E
n
d E E dS cos
Площадке сопоставляют вектор dS n
Тогда: d E dS - Скалярное произведение векторов
E
Поток вектора E через поверхность S:
E
E E dS
S
S
E В м
10

11.

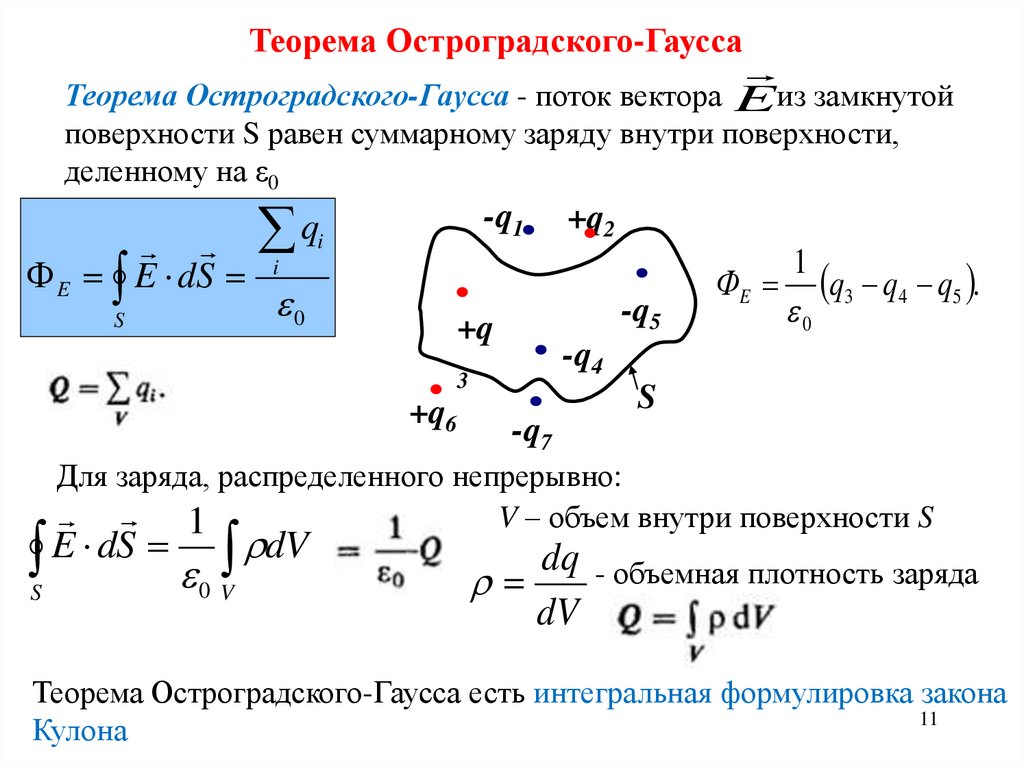
Теорема Остроградского-Гаусса
Теорема Остроградского-Гаусса - поток вектора E из замкнутой
поверхности S равен суммарному заряду внутри поверхности,
деленному на ε0
E E dS
S
q
-q1
i
+q2
i
0
-q5
+q
1
q3 q4 q5 .
0
-q4
3
+q6
ФE
S
-q7
Для заряда, распределенного непрерывно:
1
V – объем внутри поверхности S
E dS dV
S
0 V
dq - объемная плотность заряда
dV
Теорема Остроградского-Гаусса есть интегральная формулировка закона
11
Кулона

12.

Дифференциальная фора электростатической теоремы
Гаусса (закона Кулона)
В математике доказывается формула Остроградского-Гаусса:
divE - дивергенция вектора Е
E dS div EdV
S
Дивергенция характеризует
мощность источников
V
E x E y E z
div E
x
y
z
Таким образом, с учетом
S
получим:
1
divEdV dV
V
1
E dS dV
0 V
или
0 V
div E
0
Дифференциальная формулировка закона Кулона
Диф. форма электростатической теоремы Гаусса
12

13.

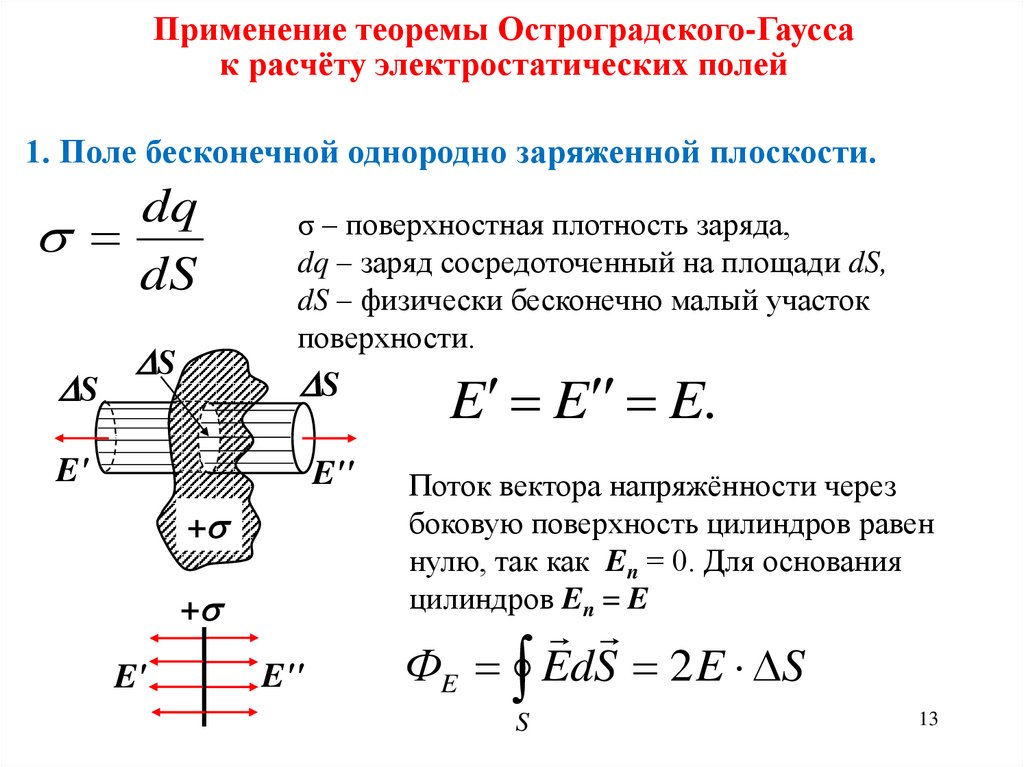
Применение теоремы Остроградского-Гаусса
к расчёту электростатических полей
1. Поле бесконечной однородно заряженной плоскости.
dq
dS
S
S
σ – поверхностная плотность заряда,
dq – заряд сосредоточенный на площади dS,
dS – физически бесконечно малый участок
поверхности.
S
E'
E''
+
+
E'
E''
E E E.
Поток вектора напряжённости через
боковую поверхность цилиндров равен
нулю, так как En = 0. Для основания
цилиндров En = E
ФE EdS 2 E S
S
13

14.

q S
E
2 0
q
Ф
.
E
0
2 S E S
1
0
.
Полученный результат не зависит от расстояния. Это
означает, что на любом расстоянии от плоскости
напряженность поля одинакова.
E = const
2. Поле двух разноименно заряженных плоскостей.
E+
-
E
.
2 0
E-
E
.
2 0
+
E+
E E E .
0
Вне пластин: E = E+ – E– = 0.
E-
14

15.

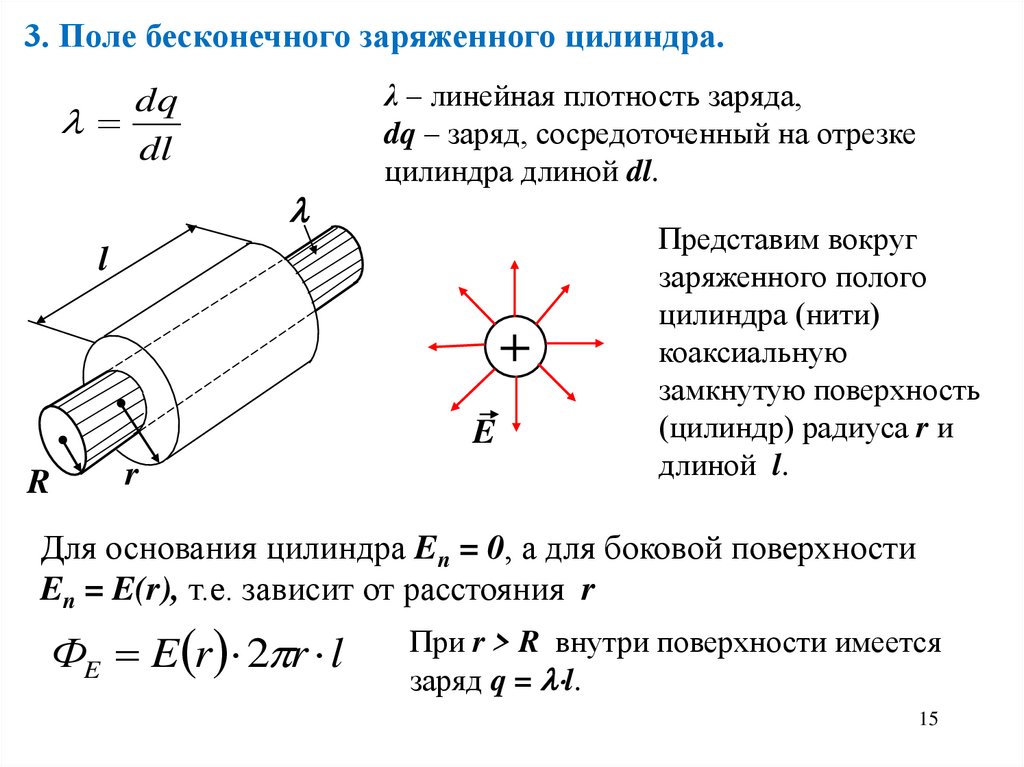
3. Поле бесконечного заряженного цилиндра.
dq
dl
λ – линейная плотность заряда,
dq – заряд, сосредоточенный на отрезке
цилиндра длиной dl.
l
E
R
r
Представим вокруг
заряженного полого
цилиндра (нити)
коаксиальную
замкнутую поверхность
(цилиндр) радиуса r и
длиной l.
Для основания цилиндра En = 0, а для боковой поверхности
En = E(r), т.е. зависит от расстояния r
ФE E r 2 r l
При r > R внутри поверхности имеется
заряд q = l.
15

16.

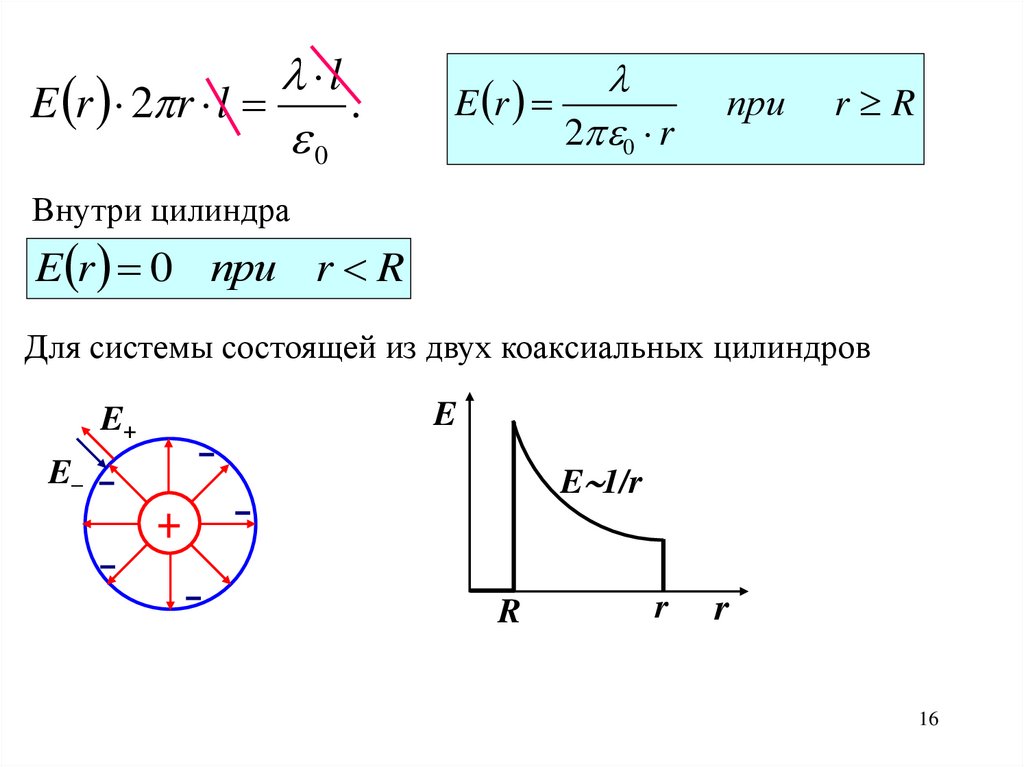
l
E r 2 r l
.
0
E r
2 0 r
при
r R
Внутри цилиндра
E r 0 при r R
Для системы состоящей из двух коаксиальных цилиндров
E+
E
E 1/r
E–
R
r
r
16

17.

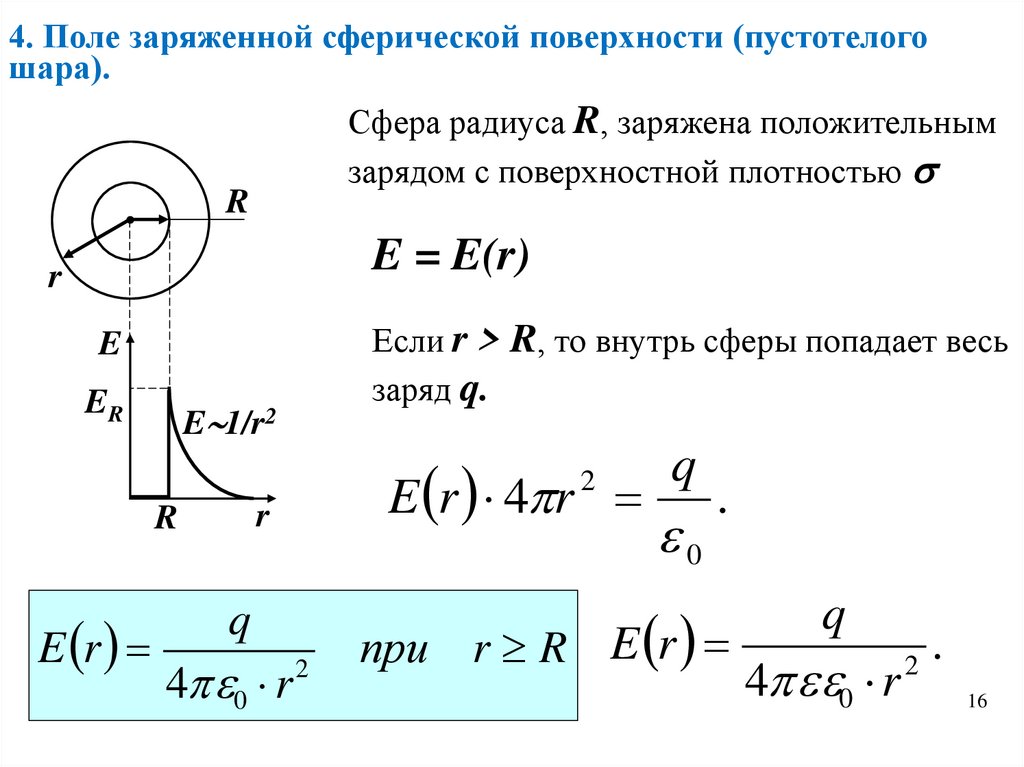
4. Поле заряженной сферической поверхности (пустотелого
шара).
Сфера радиуса R, заряжена положительным
зарядом с поверхностной плотностью
R
E = E(r)
r
Если r > R, то внутрь сферы попадает весь
заряд q.
E
ER
E 1/r2
E r 4 r
2
r
R
E r
q
4 0 r
2
q
0
.
при r R E r
q
4 0 r
2
.
16

18.

E r 0 при r R
E r
q
4 0 R
2
.
Вне сферы поле тождественно полю точечного заряда, той же
величины, помещённого в центр сферы.
5. Поле объёмно-заряженного шара.
dq
dV
Введём объёмную плотность заряда .
В данном случае сферическая поверхность при r < R будет
содержать в себе заряд q.
4 3
q r .
3
4 3
E r 4 r
r .
0
3
2
1
18

19.

E
q
4
3
R
3
.
E r
E 1/r2
R
q r
q
r
E r
3.
3
4 0 R
4 0 R
r
4 3
R r
r
3
E r
.
3
3 0
4 0 R
r
E r
.
3 0
19

20.

Потенциал
Потенциальность электростатического поля
Из механики:
Поле потенциально, если работа сил поля по перемещению частицы не
зависит от траектории, но определяется положением начальной и
конечной точек перемещения. Силы такого поля – консервативны.
F
dr
1
q'
r1
2
dl
r
q
r2
dA Fdl Fdl cos
1 qq '
F
dl cos dr
2
4 0 r
2
2
qq ' dr
A12 Fdl
2
4
r
0 1
1
qq ' 1 1
A12
4 0 r1 r2
(1)
Т.е. работа А не зависит от траектории, а значит
электростатическое поле потенциально
20

21.

2
A12
1 2
E cos dl
q0 1
разность потенциалов
Если одна из точек расположена в пространстве, где поля нет,
тогда φ2=0
1 E cos dl
1
A0
q0
Потенциал данной точки электрического поля равен
отношению работы переноса пробного заряда из данной
точки поля в другую точку, где электрическое поле
отсутствует (например, в бесконечность), к величине
переносимого заряда

22.

Работа перемещения некоторого заряда из одной точки поля в
другую равна произведению этого заряда на разность потенциалов
начальной и конечной точек перемещения:
A q( 1 2 )
Если пробный заряд q совершил малое перемещение Δl вдоль силовой
линии из точки (1) в точку (2), то можно записать:
ΔА12 = q·E ·Δl = q·(φ1-φ2) = - q·Δφ
d
E
( l 0); E
l
dl
Это соотношение в скалярной форме выражает связь между напряженностью
поля и потенциалом. l – координата, отсчитываемая вдоль силовой линии.
Напряженность в данной точке поля равна изменению потенциала на
единицу длины вдоль нормали к эквипотенциальной поверхности,
проходящей через эту точку. («минус» показывает направление в
сторону убывания потенциала)

23.

В потенциальном поле работа равна
A12 W1 W2 (2)
Сравнивая (2) и (1), получаем:
qq '
Потенциальная энергия точечного заряда q’
W
Выберем const из условия r=∞, W=0
Const =0
W
q'
- потенциал
4 0 r
const
W q '
Для поля точечного заряда потенциал равен
Для поля, созданного зарядом, распределенным
непрерывно:
q
4 0 r
dV
V 4 0r
Потенциал и потенциальная энергия – аддитивные величины
W Wi
i
i
i
23

24.

Потенциал φ∞ поля точечного заряда q0 на расстоянии r
от него относительно бесконечно удаленной точки
вычисляется следующим образом:
E
1 E cos dl
1
q
4 0 r 2
cosα = +1;
dl = dr
1
q
dr
1 q
E cos dl Edr
2
4 0 r r
4 0 r
r
r
потенциал точечного заряда по абсолютной величине убывает
обратно пропорционально расстоянию.
Wp
q0
потенциал данной точки поля точечного заряда
численно равен потенциальной энергии
системы, состоящей из заряда q и единичного
заряда q0, помещенного в эту точку поля

25.

Потенциал – скалярная величина, зависит от знака работы переноса А0
Потенциалы всех точек поля вокруг положительных зарядов –
положительные
отрицательных зарядов - отрицательные
Разность потенциалов между двумя точками равна 1 В (вольту), если
работа переноса одного кулона электричества из одной точки в другую
равна одному джоулю:
1 вольт
1 джоуль
1 кулон
1В = 1Дж/Кл
В атомной физике работа перемещения элементарных зарядов в
электрическом поле измеряется в электрон-вольтах (эВ)
1эВ равен работе перемещения электрона, если разность потенциалов
начальной и конечной точек перемещения равна 1В
1эВ = 1,6·10-19 Кл · 1В = 1,6·10-19 Дж

26.

Электрический диполь
Электрическим диполем называется система двух одинаковых по
величине, но разноимённых точечных зарядов, расстояние между
которыми l значительно меньше расстояния r до тех точек, в которых
определяется поле системы (r >> l).
Электрический момент диполя
вектор, который направлен по оси p ql
диполя от отрицательного заряда к
E+
положительному.
E
При r >> l
E-
r
–q l 2
l 2
P
+q
1
q
E E
4 0 r 2 l
E
l
l
1
2
2
E
r
l
r 2
4
x
1 p
E
4 0 r 3
q
2
4 0 r 2
2
l
q l
E
E
.
3
r 4 0 r
E||
1 2p
4 0 r 3
26

27.

Потенциальная энергия диполя во внешнем поле
складывается из энергии его зарядов:
W q q q( ).
Здесь и – потенциалы внешнего
поля в тех точках пространства,
q и q.
где расположены заряды диполя
Потенциал поля убывает в направлении вектора напряжённости:
l cos Exl cos ; Ex E W pE cos pE.
x
В неоднородном поле силы не равны по величине,
поэтому диполь втягивается в область более
сильного поля:
Fx q( E1x E2 x ),
E1x E2 x
E
l cos ,
x
E
E
Fx q
l cos p
cos .
x
x