Similar presentations:
Электричество и магнетизм. Электрический диполь
1.
Электричество и магнетизмЛекция 03
Электрический диполь
15 сентября 2021 года
Лектор: доцент НИЯУ МИФИ,
Ольчак Андрей Станиславович
2.
Курс общей физики НИЯУ МИФИЛекция 3
• Электрическое поле точечного диполя.
• Диполь во внешнем электрическом поле
• Поле системы зарядов на больших
расстояниях.
• Примеры решения задач
3.
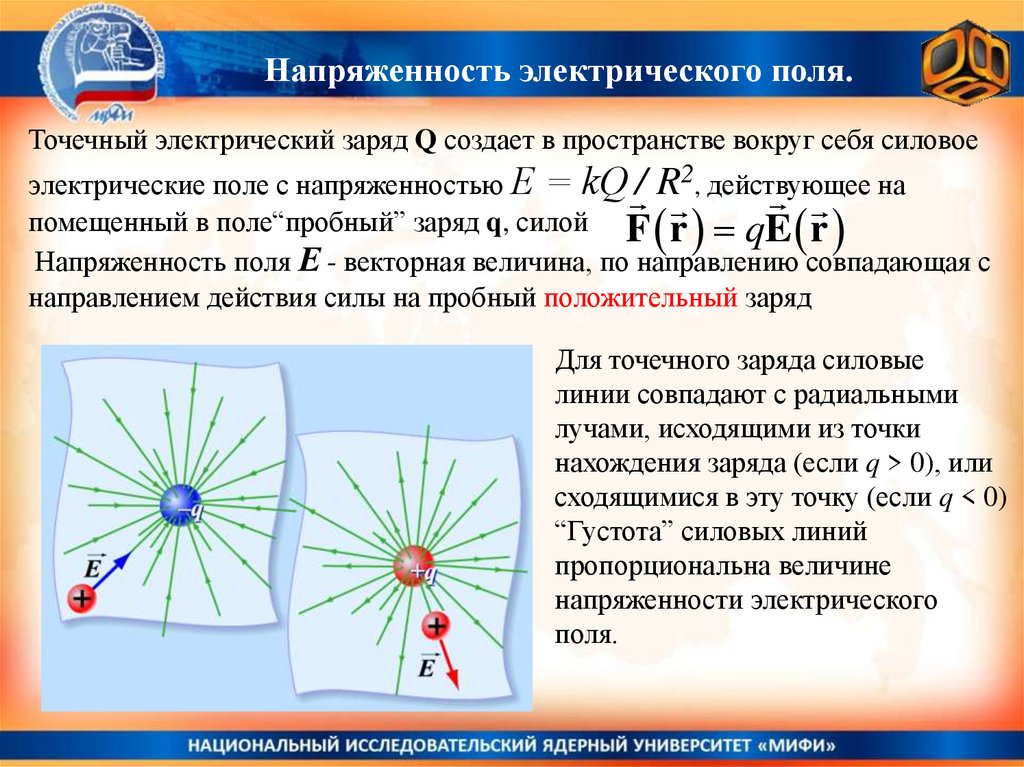
Напряженность электрического поля.Точечный электрический заряд Q создает в пространстве вокруг себя силовое
электрические поле с напряженностью Е = kQ / R2, действующее на
помещенный в поле“пробный” заряд q, силой F r qE r
Напряженность поля Е - векторная величина, по направлению совпадающая с
направлением действия силы на пробный положительный заряд
Для точечного заряда силовые
линии совпадают с радиальными
лучами, исходящими из точки
нахождения заряда (если q > 0), или
сходящимися в эту точку (если q < 0)
“Густота” силовых линий
пропорциональна величине
напряженности электрического
поля.
4.
Поле системы зарядовN
F Fi
z
i 1
r
ri
x
N
E Ei
i 1
N
N
R i R i r ri E r Ei k
y
qi
i 1
i 1
N
N
i 1
i 1
r i k
1 N
w qi i
2 i 1
qi r ri
r ri
qi
r ri
i
N
n 1
n i
kqn
rin
3
5.
Напряжённость и потенциалСвязь между напряжённостью электрического
поля и потенциалом
F w qE q
E
Ex
, Ey
, Ez
x
y
z
2
2
1
1
A12 q 1 2 q Edr 1 2 Edr
6.
Суперпозиция электрических полей.Линии напряжённости; начинаются на положительных зарядах и «уходят» в
бесконечность, либо «приходят» из бесконечности и заканчиваются на
отрицательных зарядах. Касательные к линиям напряженности в каждой
точке совпадают с направлением вектора напряженности
Поверхности, на которых потенциал принимает постоянное значение,
называются эквипотенциальными поверхностями.
7.
Электрическое поле диполяq
l
q
p ql
p - электрический
дипольный момент
8.
Немного математикиПриращение и дифференциал функции трёх переменных
f
f
f
f f r dr f r df dx dy dz
x
y
z
f f f
f , , dr dx, dy , dz
x y z
df f dr
9.
Электрическое поле диполяdf f dr
r
q
r
=
- т r l
+ т r т l
kq r
r
Eт l 2 l k 3 q l
r r
r
l
l
A
kq
kq
д r
r r l
r l
q
kq
т r т r
r
r p
д k 3
r
p ql
10.
Электрическое поле диполяr p rp cos
r
p
p cos
д k
r2
1
r2
11.
Электрическое поле диполяНапряжённость электрического поля диполя
r p
1
Eд д k 3 k r p 3
1
r p
3
r
r r
df r
1
3 r
3r
Математическое
f r
3 4 5
дополнение.
dr r
r
r r
r
r p xp x yp y zpz xp x yp y zp z e x ...
x
px e x p y e y pz e z p
1
k 3 r p r
Eд 3
p
2
3
r r
r
12.
Электрическое поле диполяE
Er e r
E e
Eд Er e r E e
2kp cos
Er
r3
kp sin
E
r3
13.
Диполь в электрическом полеПотенциальная энергия диполя
во внешнем электрическом поле
E
F
r
o
l
F
M
r l
w q r l q r
q r l r
q l p E
p q l , E
w p E pE cos
14.
Диполь в электрическом полеМомент сил, действующих на диполь
во внешнем электрическом поле
E
F
r
o
l
F
M
r l
E r l E r F F
l sin - плечо пары сил
M F l sin qEl sin pE sin
E
p
M
M p E
15.
Диполь в электрическом полеМатематическое дополнение. Приращение и
дифференциал векторной функции трёх переменных
f fx , f y , fz
f x f x r dr f x r df x
dr f x dr f x ,
dr dx dy dz
x
y
z
f
f
f
df dr f dx dy dz
x
y
z
16.
Диполь в электрическом полеСила, действующая на диполь
во внешнем электрическом поле
F F F qE r l qE r
E
F
q l E q l E p E
F
l
E
E
E
F p E px
py
pz
r l
x
y
z
r
o
df dr f
Замечание: В статическом
электрическом поле
F w p E
17.
Диполь в электрическом полеПример 1. Однородное электрическое поле
E const F 0
Пример 2. Слабо неоднородное электрическое поле
E E x ex
E
p px
Fx px
x
x
Ex
px 0,
0 Fx 0
x
18.
Поле системы зарядовri r di
d << r; di <<ri
r i ri i r di
ri
d
qi
n
n
i 1
i 1
i r di i r i di
r
di
O
kqi kqir
=
i r Ei d i
3 di
r N r
N
Р – дипольный момент k q k r q d
i
i i
3
r i 1
r i 1
системы зарядов
N
N
i 1
i 1
Q qi , P qidi
kQ k r P
r
...
3
r
r
19.
Дипольный момент системы зарядовq
q
l
P = qr+ - qr- = ql
r-
p ql
r+
O
N
N
i 1
i 1
Q qi , P qidi
r p rp cos
kQ k r P
r
...
3
r
r
p cos
д k
r2
1
r2
20.
Курс общей физики НИЯУ МИФИЭлектричество и магнетизм
Из Лекции 4
Теорема Гаусса.
21.
Пример задачиx
Заряд равномерно
q
распределён по тонкому
кольцу радиуса . НайтиR
проекцию напряженности
поля на оси кольца как
функцию расстояния до
центра кольца.
x
qdl qRd qd
dq
2 R 2 R
2
E
dE
r
dl
dq
x
d
R
22.
Примеры задач1 dq
dE
r
3
4 0 r
r x2 R2
Ex
Ex
4 0 r
3
4 0 x R
2
r
dq
qx
dq
2 32
E
dE
r cos dq
xdq
dE x
3
4 0 r
4 0 r 3
x
x
x
d
R
23.
Примеры задачx
Пример 3. Заряд распределён по
q R так, что
тонкому кольцу радиуса
плотность заряда λ = λ0 cos φ . φ
– уuол к оси 0Y. Найти
напряженность поля на оси кольца
E
dE
r
x
dq(φ) = dl λ0 cos φ
dEy = kdl λ0 |cos(φ)| sin(a) / (R2+x2)
= kR2dφ λ0 |cos(φ)| / (R2+x2)3/2.
Ey = 4kR2λ0 / (R2+x2)3/2 ~ 4kR2λ0 /x3.
.
dl
dq
d
R
24.
Поток вектораu
dS
n
dS
d udS cos
dS dSn
d u dS
Определение:
Если площадка dS дифференциально мала (почти
точечная), то элементарный поток вектора u
через нее dФ = (u,dS) – Вектор dS считаем
направленным по нормали к площадке.
Поток вектора Ф через большую поверхность S
вычисляется как сумма (интеграл) элементарных
потоков ΔФ через все микроскопические площадки
dS , составляющие большую.
Ф=0
E
ΔS
25.
Поток вектораu
dS
n
dS
d udS cos
u dS
u
n
S
S
ОПРЕДЕЛЕНИЕ: Поток вектора Ф через большую поверхность S вычисляется как
сумма (интеграл) элементарных потоков ΔФ через все микроскопические площадки dS ,
составляющие большую. Поток пропорционален числу силовых линий,
пронизыва.щих площадку (с учетом их направления)
26.
Поток вектораПоток через замкнутую
поверхность
u dS
S
S
Геометрическая интерпретация
потока
n
Ф ~ N+ - N- = 0 (если N+ = N- )
n
u
27.
Поток вектора напряженности эл. поляОПРЕДЕЛЕНИЕ: для поля E скалярное произведение
E
ΔS
ΔФ=(E,ΔS) – элементарный поток вектора поля E яерез
площадку ΔS. Вектор ΔS направлен по нормали к площадке
Поток Ф через большую поверхность S вычисляется как сумма
(интеграл) элементарных потоков ΔФ через все малые
площадки, составляющие поверхность .
В частности: поток вектора поля E через сферическую
поверхность с центром в точке - источнике поля, очевидно равен
Ф = SE=4πr2E = 4πr2kq/r2 = 4πkq.
А если заряд не в центре? Или если поверхность не сферическая?
Число пронизывающих поверхность силовых линий останется темже => поток останется тем-же. Ф = 4πkq = q /ɛ0 ;
ɛ0 = 1/4πk – диэлектрическая постоянная
28.
Интегральная форма теоремы ГауссаЕсли внутри поверхности несколько зарядов qi , то каждый создаст
поток Фi = 4πkqi , а общий поток будет равен Ф = 4πkΣqi
E E1 E2 ... EN
EdS E dS E dS ... E
1
S
q1
0
2
S
q2
0
...
S
qN
0
S
1
0
N
q
i 1
i
Поток вектора напряженности
электрического поля через замкнутую
поверхность равен алгебраической
сумме заключенных внутри этой
поверхности зарядов, деленной на
электрическую постоянную ɛ0
N
dS
29.
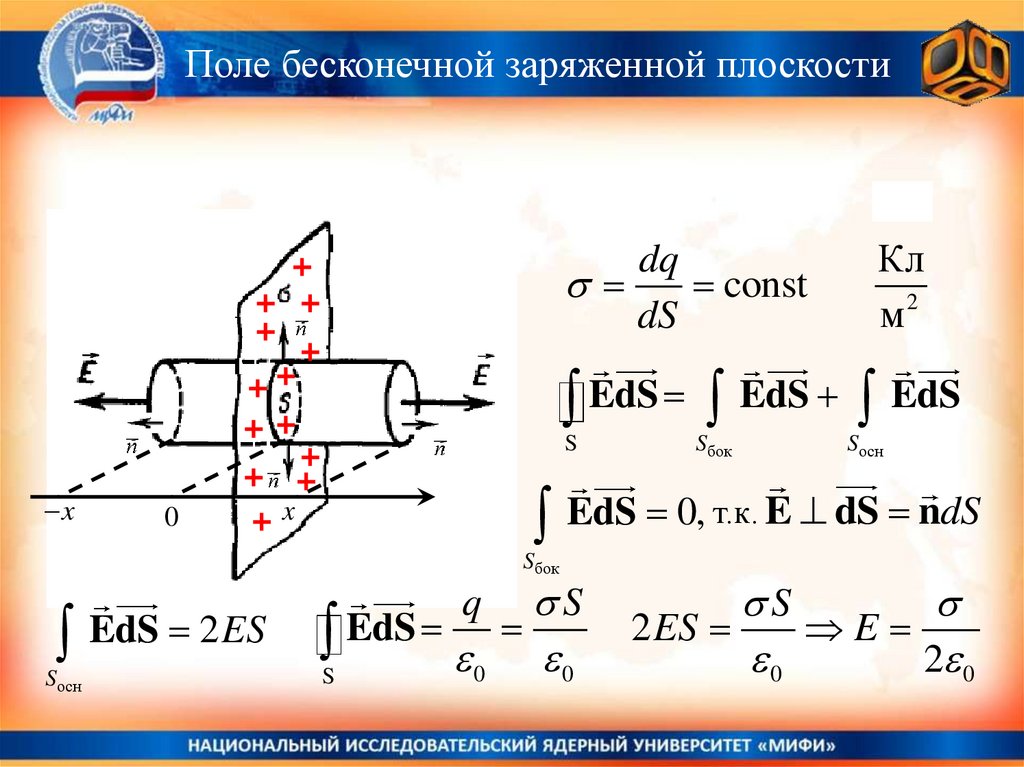
Поле бесконечной заряженной плоскостиdq
const
dS
Кл
м2
EdS EdS EdS
S
x
0
Sосн
Sосн
EdS 0, т.к. E dS ndS
x
Sбок
EdS 2 ES
Sбок
S
S EdS 0 0
q
S
2 ES
E
0
2 0
30.
Поле бесконечной заряженной плоскостиE
2 0
2 0
x
const
2 0
x
E x dx
Ex
2 0
x
31.
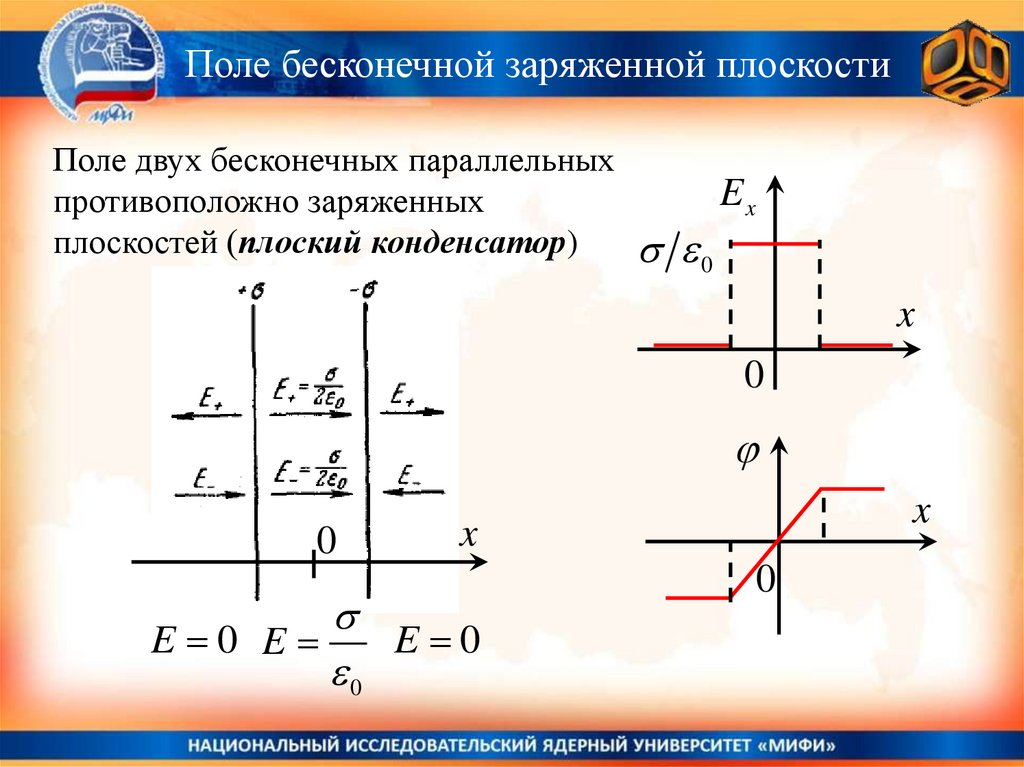
Поле бесконечной заряженной плоскостиПоле двух бесконечных параллельных
противоположно заряженных
плоскостей (плоский конденсатор)
0
Ex
x
0
0
x
x
E 0 E
E 0
0
0
32.
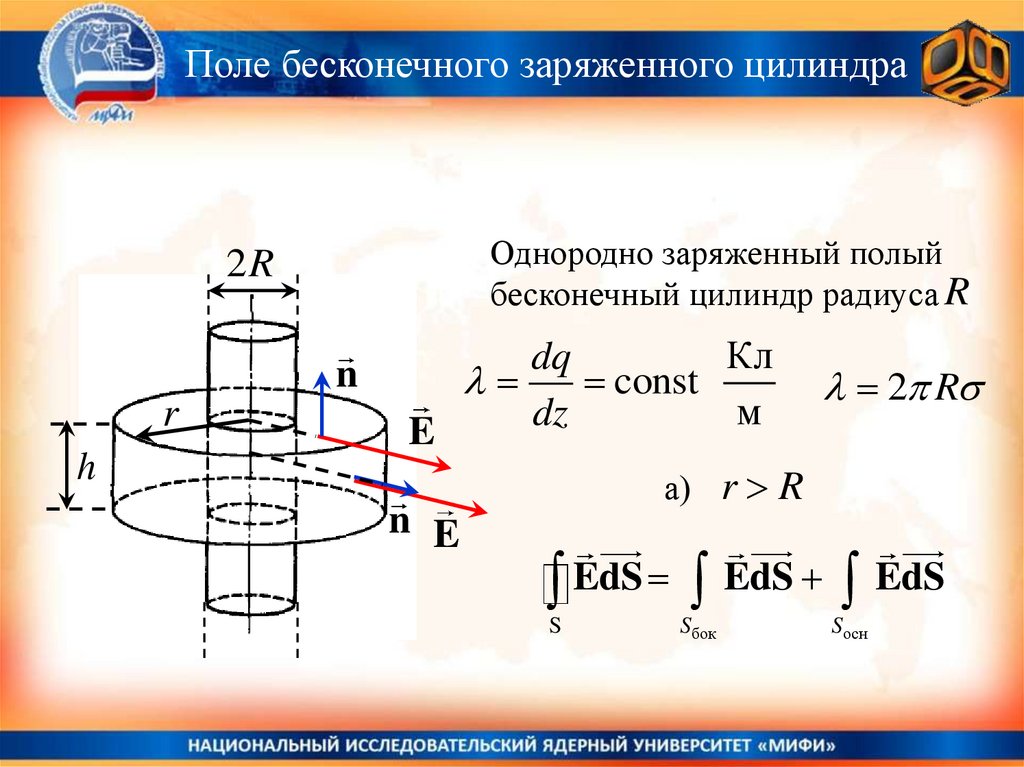
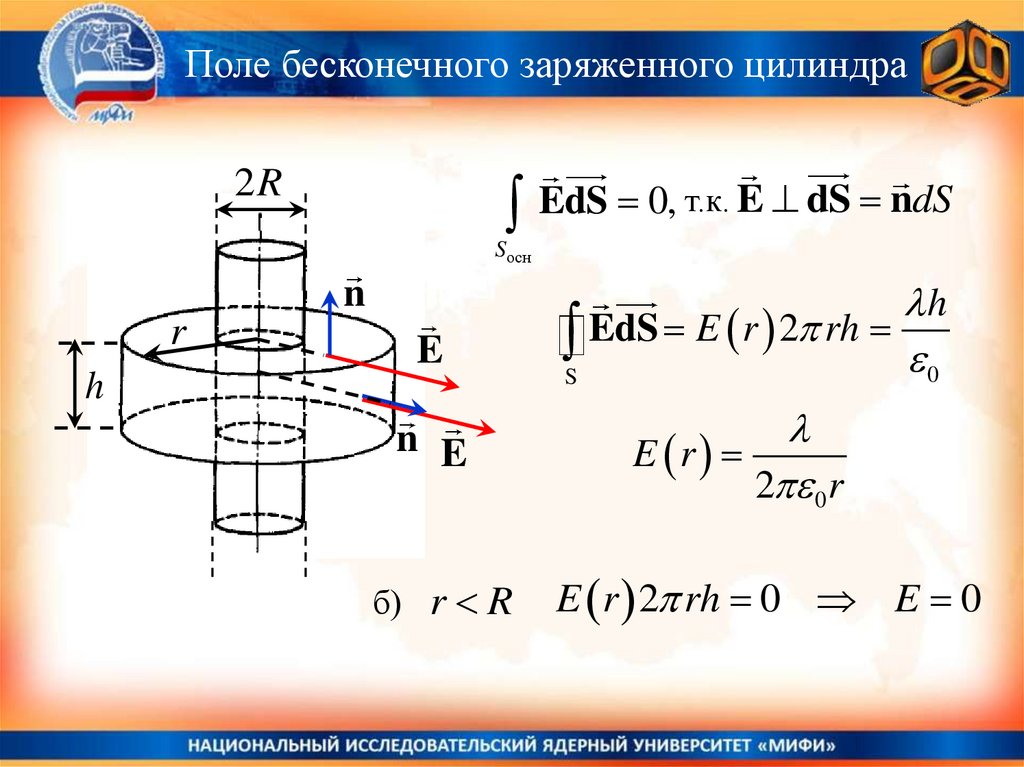
Поле бесконечного заряженного цилиндра2R
r
h
Однородно заряженный полый
бесконечный цилиндр радиуса R
Кл
dq
n
const
2 R
м
dz
E
а) r R
n E
EdS EdS EdS
S
Sбок
Sосн
33.
Поле бесконечного заряженного цилиндраEdS 0, т.к. E dS ndS
2R
Sосн
n
r
h
E
n E
б) r R
h
S EdS E r 2 rh 0
E r
2 0 r
E r 2 rh 0 E 0
34.
Поле бесконечного заряженного цилиндра2 r ,
E r
0
0,
r R ;
0 r R
0
Er
φ(r<R) = φ0
φ(r>R) = (λ/2πε0)ln(R/r) + φ0
r
0
R
35.
Поле заряженных сферы и шараОднородно заряженная полая сфера
R
Кл
dq
const
м2
dS
а) r R EdS E r dS
S
S
E r dS E r 4 r
2
S
E
q
4 0 r
2
q
0
36.
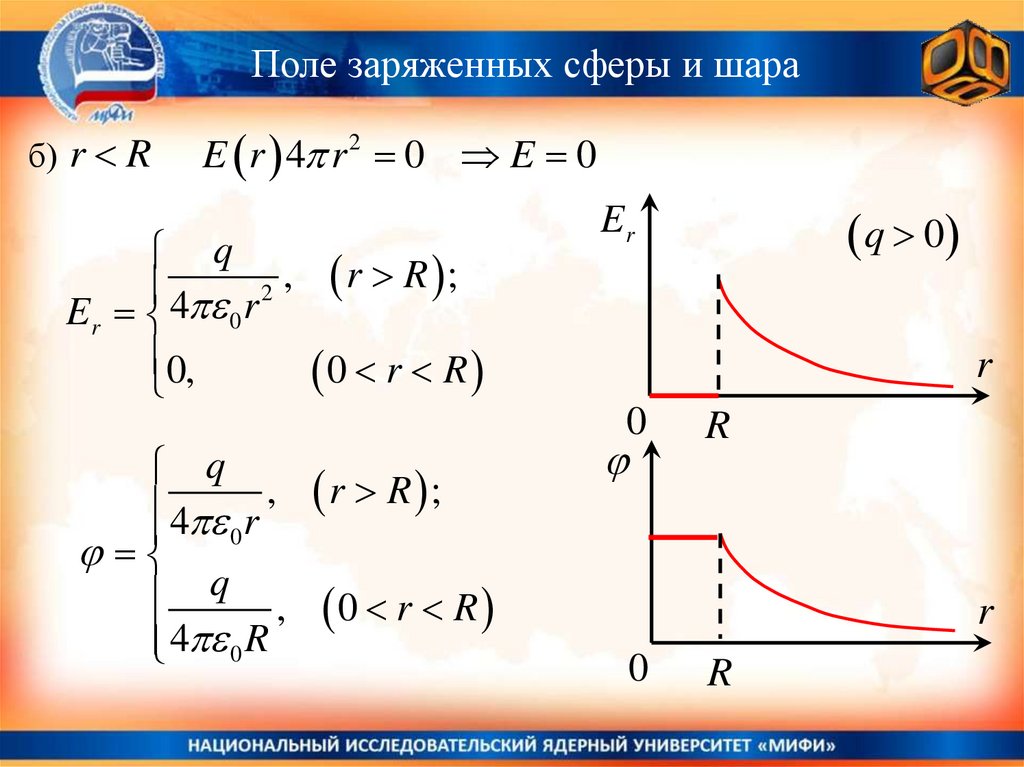
Поле заряженных сферы и шараб) r R
E r 4 r 2 0 E 0
q
4 r 2 , r R ;
Er
0
0,
0 r R
q
4 r ,
0
q ,
4 0 R
r
0
r R ;
q 0
Er
R
0 r R
r
0
R
37.
Поле заряженных сферы и шараПоле двух противоположно
заряженных концентрических сфер
(сферический конденсатор)
Er
kq
Er 2
r
r
q
0
R2
R1
R1 R2
kq
Er 2
r
Er
r
r
0
R1 R2
38.
Поле заряженных сферы и шараdq
const
dV
Поле однородно заряженного
шара
а) r R
R
r
n
Кл
м3
EdS E r dS
E
S
S
E r 4 r 2 q r 0
4 3
q r dV V
r
3
V
r
E r
3 0
3q
4 R 3
kqr
E 3
R
39.
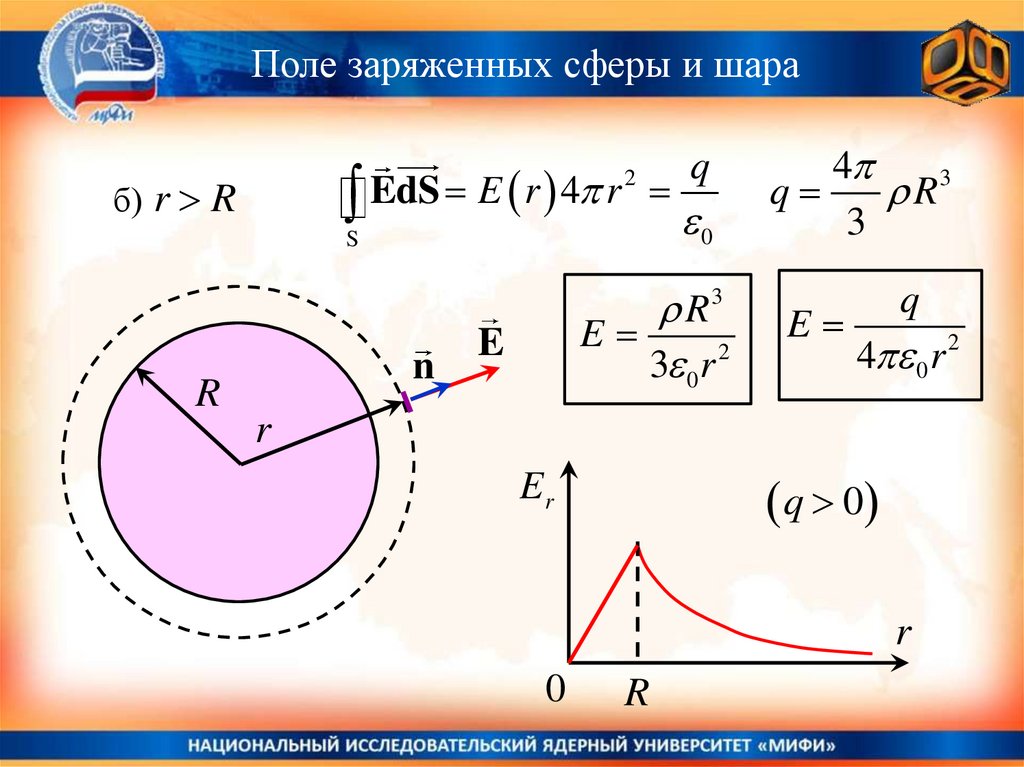
Поле заряженных сферы и шараEdS E r 4 r
б) r R
2
S
R
n
q
0
R3
E
3 0 r 2
E
4
q
R3
3
E
q
4 0 r 2
r
q 0
Er
r
0
R
40.
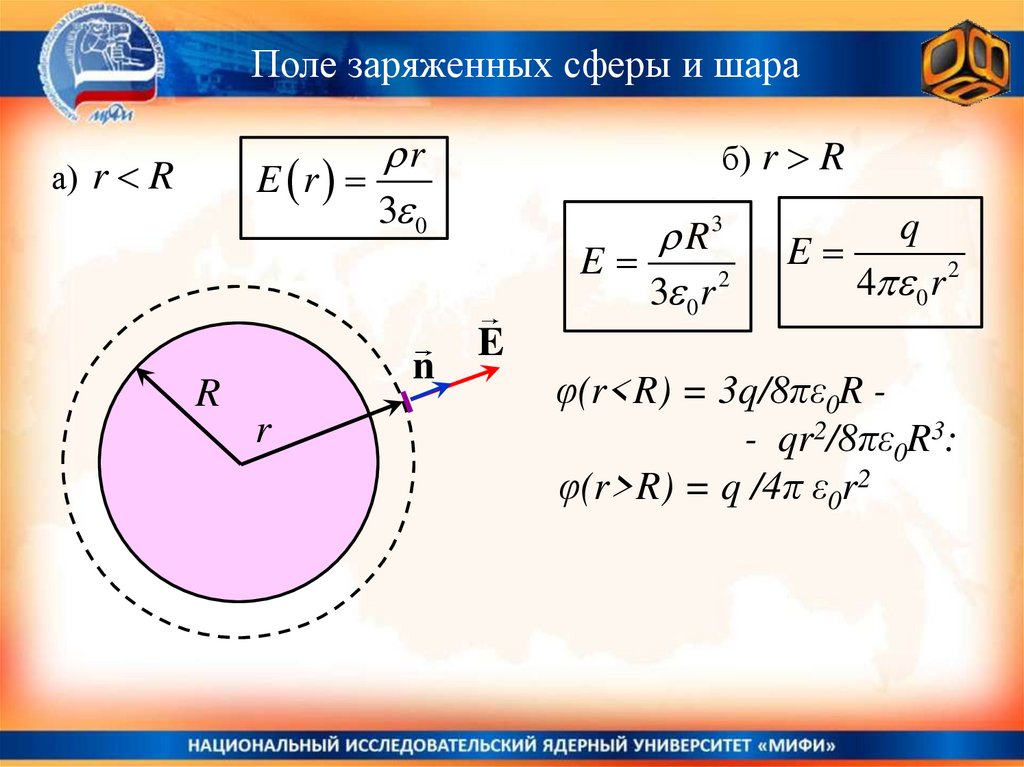
Поле заряженных сферы и шараr
E r
3 0
а) r R
R
n
r
б) r R
R3
E
3 0 r 2
E
q
4 0 r 2
E
φ(r<R) = 3q/8πε0R - qr2/8πε0R3:
φ(r>R) = q /4π ε0r2
41.
Курс общей физики НИЯУ МИФИСпасибо за внимание!
Следующая лекция
22 сентября
42.
Пример задачиКвадруполь. Заряды q и -q, показанные на рисунке, расположены
в вершинах квадрата со стороной a. Вычислить потенциал и
напряженность поля, создаваемого этими зарядами на далеких
расстояниях, т.е. при условии r, x, y >> a
.
y
N
x
P qi di
i 1
kQ k r P
r
...
3
r
r
r
φ(r) = kq[((x-a/2)2+(y+a/2)2)-1/2 + ((x+a/2)2+(y-a/2)2)-1/2 –
- ((x-a/2)2+(y-a/2)2)-1/2 - ((x+a/2)2+(y+a/2)2)-1/2] ~= 3kqa2xy/r5
(Taylor, разложение до квадратичных поправок…)
43.
Пример задачиЗаряды, показанные на рисунке, расположены в вершинах
квадрата со стороной a. Вычислить потенциал и
напряженность поля, создаваемого этими зарядами на
далеких расстояниях, т.е. при условии r >> a
.
p ql
N
P qi di
i 1
p 2qae y
2qa e y r
r p
k 3
3
r
4 0 r



































 physics
physics








