Электричество и магнетизм. Лекция 4

1.

Курс общей физики НИЯУ МИФИ
Электричество и магнетизм
Лекция 4
Теорема Гаусса.
Поток и дивергенция векторного поля
22 сентября 2021 года
Лектор: доцент НИЯУ МИФИ,
Ольчак Андрей Станиславович

2.

Немного математики.
u
dS
n
dS
d udS cos
dS dSn
d u dS
Поток вектора
Определение:
Если площадка dS дифференциально мала (почти
точечная), то элементарный поток вектора u
через нее dФ = (u,dS) – Вектор dS считаем
направленным по нормали к площадке.
Поток вектора Ф через большую поверхность S
вычисляется как сумма (интеграл) элементарных
потоков ΔФ через все микроскопические площадки
dS , составляющие большую.
Ф=0
E
ΔS

3.

Немного математики.
Поток вектора
u
dS
n
dS
d udS cos
u dS
u
n
S
S
ОПРЕДЕЛЕНИЕ: Поток вектора Ф через большую поверхность S вычисляется как
сумма (интеграл) элементарных потоков ΔФ через все микроскопические площадки dS ,
составляющие большую. Поток пропорционален числу силовых линий,
пронизыва.щих площадку (с учетом их направления)

4.

Примеры задач
Пример. Найдите поток однородного горизонтального
электрического поля с напряжённостью E через поверхность,
показанную на рисунке. «Тень» поверхности на вертикальную
плоскость образует прямоугольник с размерами a и b.
E
b
a
E
n
dS
dS
d EdS cos EdS dS dS cos
EdS E dS ES Eab
S
S

5.

Немного математики.
Поток вектора
Поток через замкнутую
поверхность
u dS
S
S
Геометрическая интерпретация
потока
n
Ф ~ N+ - N- = 0 (если N+ = N- )
n
u

6.

Поток вектора напряженности эл. поля
ОПРЕДЕЛЕНИЕ: для поля E скалярное произведение
E
ΔS
ΔФ=(E,ΔS) – элементарный поток вектора поля E яерез
площадку ΔS. Вектор ΔS направлен по нормали к площадке
Поток Ф через большую поверхность S вычисляется как сумма
(интеграл) элементарных потоков ΔФ через все малые
площадки, составляющие поверхность .
В частности: поток вектора поля E через сферическую
поверхность с центром в точке - источнике поля, очевидно равен
Ф = SE=4πr2E = 4πr2kq/r2 = 4πkq.
А если заряд не в центре? Или если поверхность не сферическая?
Число пронизывающих поверхность силовых линий останется темже => поток останется тем-же. Ф = 4πkq
ɛ0 = 1/4πk – диэлектрическая постоянная
= q /ɛ0 ;

7.

Интегральная форма теоремы Гаусса
Если внутри поверхности несколько зарядов qi , то каждый создаст
поток Фi = 4πkqi , а общий поток будет равен Ф = 4πkΣqi
E E1 E2 ... EN
EdS E dS E dS ... E
1
S
q1
0
2
S
q2
0
...
S
qN
0
S
1
0
N
q
i 1
i
Поток вектора напряженности
электрического поля через замкнутую
поверхность равен алгебраической
сумме заключенных внутри этой
поверхности зарядов, деленной на
электрическую постоянную ɛ0
N
dS

8.

Поле бесконечной заряженной плоскости
dq
const
dS
Кл
м2
EdS EdS EdS
S
x
0
Sосн
Sосн
EdS 0, т.к. E dS ndS
x
Sбок
EdS 2 ES
Sбок
S
S EdS 0 0
q
S
2 ES
E
0
2 0

9.

Поле бесконечной заряженной плоскости
E
2 0
2 0
x
const
2 0
x
E x dx
Ex
2 0
x

10.

Поле бесконечной заряженной плоскости
Поле двух бесконечных параллельных
противоположно заряженных
плоскостей (плоский конденсатор)
0
Ex
x
0
0
x
x
E 0 E
E 0
0
0

11.

Поле бесконечного заряженного цилиндра
Однородно заряженный полый
бесконечный цилиндр радиуса R
2R
n
r
h
dq
const Кл 2 R
dz
м
E
r R EdS E r 2 rh h
S
n E
0
E r
2 0 r
r R E r 2 rh 0 E 0

12.

Поле бесконечного заряженного цилиндра
2 r ,
E r
0
0,
r R ;
0 r R
0
Er
φ(r<R) = φ0
φ(r>R) = (λ/2πε0)ln(R/r) + φ0
r
0
R

13.

Поле заряженной сферы
dq
const
dS
R
r R
E r 4 r 2 0 E 0
r R
EdS E r dS
S
E r dS E r 4 r
2
S
Кл
м2
q
0
S
E
q
4 0 r 2

14.

Поле заряженных сферы и шара
q
4 r 2 , r R ;
Er
0
0,
0 r R
q
4 r ,
0
q ,
4 0 R
r
0
r R ;
q 0
Er
R
0 r R
r
0
R

15.

Поле заряженных сферы и шара
dq
const
dV
Поле однородно заряженного
шара
а) r R
R
r
n
Кл
м3
EdS E r dS
E
S
S
E r 4 r 2 q r 0
4 3
q r dV V
r
3
V
r
E r
3 0
3q
4 R 3
kqr
E 3
R

16.

Поле заряженных сферы и шара
EdS E r 4 r
б) r R
2
S
R
n
q
0
R3
E
3 0 r 2
E
4
q
R3
3
E
q
4 0 r 2
r
q 0
Er
r
0
R

17.

Поле заряженных сферы и шара
r
E r
3 0
а) r R
R
n
r
б) r R
R3
E
3 0 r 2
E
q
4 0 r 2
E
φ(r<R) = 3q/8πε0R - qr2/8πε0R3:
φ(r>R) = q /4πε0r
Функция непрерывная и
гладкая

18.

Поток и дивергенция
Сосчитаем поток вектора u через поверхность микро-кубика:
d 11 u x dx, y, z dSn1 u x, y, z dSn1
y
z
ux x dx, y, z ux x, y , z dS
n3
n2
ux
ux
dxdS
dV
n1 dV
x
x
n1
u y
n 2
d 22
dV
y
x
O
n 3
uz
d 33
dV
z
dx dy
u x u y uz
d d 11 d 22 d 33
dV
y
z
x

19.

Поток и дивергенция
d d 11 d 22 d 33
d
div u
dV
u x u y uz
dV
y
z
x
ux u y uz
div u
x
y
z
u x u y uz
=
,
,
div u u
x y z
Дивергенция вектора = объёмная плотность потока вектора.

20.

Теорема Гаусса. Дифференц. форма
Поток вектора напряженности электрического поля через
замкнутую поверхность равен алгебраической сумме
заключенных внутри этой поверхности зарядов, деленной
на электрическую постоянную ɛ0 = 4πk
1
N
EdS q
S
0 i 1
i
divE = dФ/dV =
= (Σ qi / ɛ0 )dV =
= ρ / ɛ0
div E
0
Дивергенция вектора напряженности электрического поля
в точке равна плотности электрического заряда в данной
точке, деленной на электрическую постоянную ɛ0.
= Первое уравнение Максвелла

21.

Теорема Остроградского-Гаусса
Факт: поток через внешнюю поверхность
группы микро-кубиков = сумме потоков
через поверхности всех микро-кубиков
Vi
V
V
N
Га́усс И. К. Ф.
(1777-1855)
N
u dS
S
i 1
i
div ui Vi div u dV
i 1
V
NV 0
i
Острогра́дский
М. В. (1801-1861)
u dS div u dV
S
V

22.

Примеры задач
Пример . В некоторой области пространства дивергенция
электрического поля равна нулю. Рассмотрим замкнутую
поверхность S , которая делится на две части S1 и S 2 . Найдите
отношение потоков вектора E через поверхности S1 и S.2
S
S1
1 2 E dS E dS
S1
S2
S2
E dS divE dV 0
S
V
1 2 0 1 2 1

23.

Курс общей физики НИЯУ МИФИ
Спасибо за внимание!

24.

Электричество и магнетизм
Из лекции 05
Электрическое поле в диэлектриках
22 сентября 2021 года
Лектор: доцент НИЯУ МИФИ,
Ольчак Андрей Станиславович

25.

Проводники и диэлектрики
Диэлектрик – вещество, где нет свободных электрических
зарядов, способных перемещаться под действием приложенного
электрического поля (= проводить электрический ток).
Проводник – вещество, где способные перемещаться заряды есть
и электрический ток (упорядоченное направленное движение
электрических зарядов) существовать может .

26.

Диэлектрики
Полярные (в частности - вода) – молекулы обладают
дипольным электрическим моментом, ориентируются против
приложенного внешнего поля. .
-
105
+
Неполярные (инертные газы, органика, пластик и др.) – могут
приобретать дипольный момент в эл. поле (поляризуемость).
-
+
CO 2
Заряды, создающие внешнее поле, называются сторонними.
Заряды, входящие в состав молекул диэлектрика, называются связанными.

27.

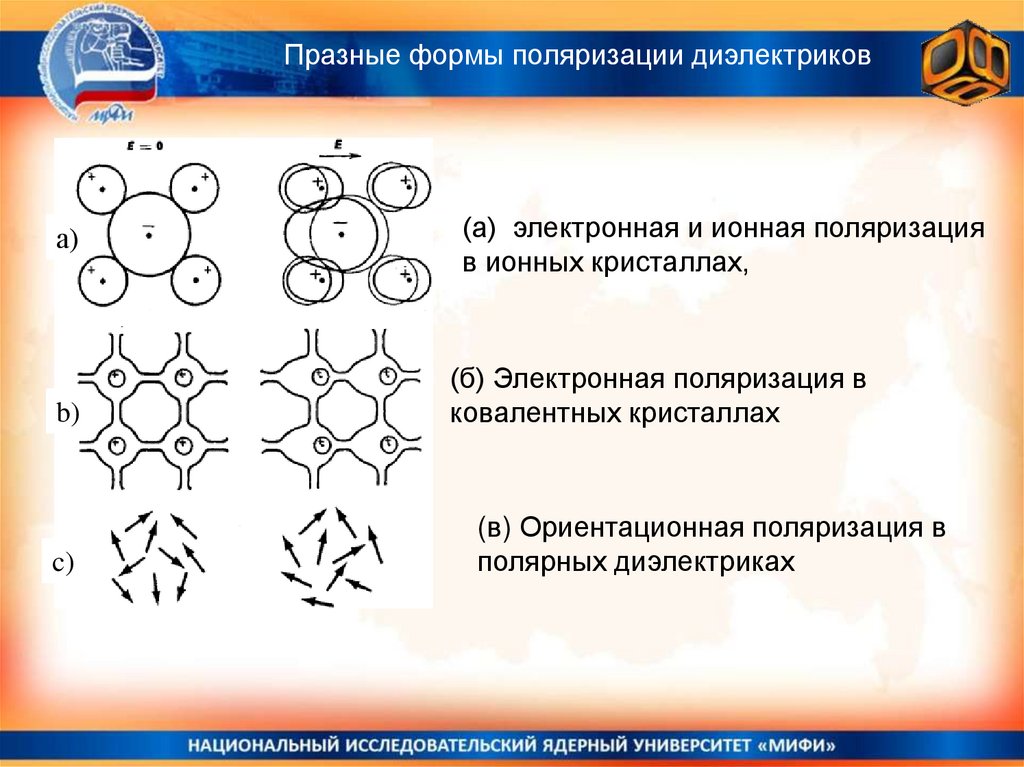
Празные формы поляризации диэлектриков
а)
b)
c)
(а) электронная и ионная поляризация
в ионных кристаллах,
(б) Электронная поляризация в
ковалентных кристаллах
(в) Ориентационная поляризация в
полярных диэлектриках

28.

Поляризация диэлектриков
Эффект поляризации –
см. «Физика в опытах»!

29.

Поляризация диэлектриков
E0
E0 0
Вектор поляризованности –
дипольный момент
единицы объема
поляризованного вещества
1
P
V
ΔV
N
p
i 1
i
Опыт показывает, что в изотропном
ΣPi=0
ΣPi=0
/
диэлектрике P
= ε0ξE
ξ ( >0 ) – диэлектрическая восприимчивость.
Диэлектрик называется однородным, если во всех его точках
диэлектрическая восприимчивость одинакова: ξ
= Const

30.

Характеристики диэлектриков
Вектор поляризованности – дипольный момент
единицы объема поляризованного вещества
В изотропном диэлектрике
P = ε0ξE
1
P
V
N
p
i 1
i
ξ – диэлектрическая восприимчивость
ε = 1 + ξ (>1) – относительная диэлектрическая проницаемость
(безразмерный фактор, показывающий, во сколько раз снижается
поле в поляризованном диэлектрике; ε
= Е0 / Е ; ξ = ε - 1
εэл = (1 + ξ)ε0 – диэлектрическая проницаемость (размерная, Ф/м)
В однородном диэлектрике ξ
= Const>0; ε = Const>1

31.

Теорема Гаусса для поляризованности
+
+
+
-
+
+
- +
+
- ++
+ - -
Сонаправленные дипольные
моменты суммируются
Цепочки последовательно
выстроенных. диполей имеют
Момент, равный заряду, умноженному
на длину цепочки.
+σ
n
dS
P
h
σ
-σ
-n
|Σp| = hσdS = PdV =
= PhdScosθ = (P,n)hdS
Плотность
приповерхностного заряда
σ = (P,n)

32.

Теорема Гаусса для поляризованности
S, V
n
ds
P
σ = (P,n)
QS= ∫ σds = ∫v (P,n)ds = v∫ (P,dS)
Полный связанный приповерхностный заряд равен
потоку вектора поляризованности через поверхность.
QV = ∫ρ’dV – полный объемный связанный заряд внутри поверхности.
QV + QS = 0 -
условие электронейтральности вещества
Если диэлектрик поляризован неоднородно,
QV = -QS =
/0
-∫ρ’dV = v∫ (P,dS) = ∫divP dV => divP = - ρ’
В однородно поляризованном диэлектрике P
.
= Const, ρ’ = 0

33.

Электрическая индукция (смещение)
стор , связ
, P
, E
0
0 , E , P
, 0 E , P , 0E P
D 0E P
Кл
D 2
м
, D
В изотропном диэлектрике P 0 E .
D 0 E 0 E 0 E 1
1
D 0 E

34.

Электрическая индукция (смещение)
Теорема Гаусса для вектора электрического смещения
в интегральной форме
, D
Доказательство
По аналогии:
, E
0
E
, D
D q
стор , связ
q
0

35.

Курс общей физики НИЯУ МИФИ
Спасибо за внимание!
Следующая лекция
29 сентября