Similar presentations:
Электричество и магнетизм. Лекция 01. Электростатическое поле в вакууме
1.
Электричество и магнетизмЛекция 01
Электростатическое поле в вакууме
6 сентября 2013 года
Лектор: доцент НИЯУ МИФИ,
Ольчак Андрей Станиславович
2.
Электрический заряд1. Существует два типа электрических зарядов
+1
q1q2 0
+
q1q2 0
-1
2. Существует наименьший электрический заряд (элементарный)
q Ne, e 1,6 10 19 Кл
3.
Заряды элементарных частицПротоны имеют положительный заряд
ер = +1,6 •10-19 Кл
Электроны имеют отрицательный заряд
еe = -1,6 •10-19 Кл
Нейтроны - электронейтральны, их электрический
заряд равен нулю.
Заряд е = 1,6 •10-19 Кл называется элементарным.
В природе не встречаются свободные заряды, меньшие элементарного.
Все заряды кратны элементарному.
4.
Электризация.Макроскопические заряженные тела
Макроскопические тела в нормальных условиях в среднем
электро-нейтральны.
Но! Можно отделить часть отрицательного заряда (часть
электронов) от одного тела и перенести на другое наэлектризовать тела.
Это можно сделать, например, с помощью трения.
При электризации, величина избыточного заряда q1 на одном теле окажется в точности
равна и противоположна по знаку величине избыточного заряда на другом q2 = -q1.
5.
Закон сохранения зарядаЗакон сохранения электрического заряда.
В замкнутой системе алгебраическая сумма электрических
зарядов всех частиц остается неизменной.
n
q
i 1
i
q1 q2 ... qn const
6.
Электрические заряды – демонстрационные опыты«Открытое образование»,
курс «Физика в опытах», часть 3
Электрические и магнитные явления
7.
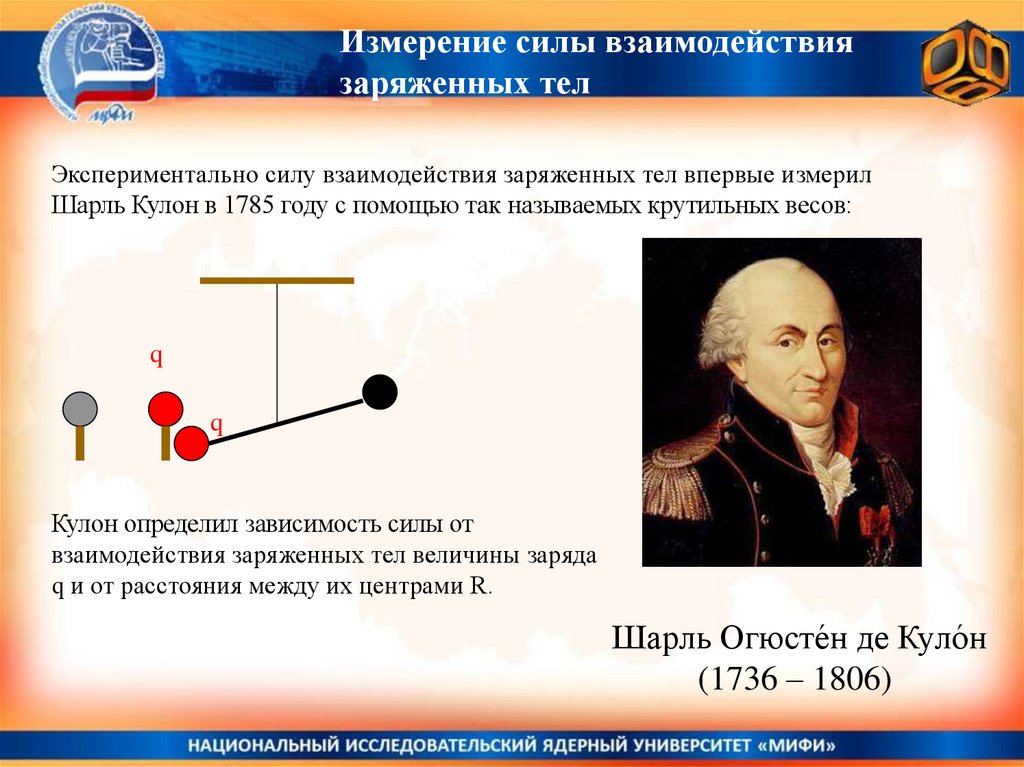
Измерение силы взаимодействиязаряженных тел
Экспериментально силу взаимодействия заряженных тел впервые измерил
Шарль Кулон в 1785 году с помощью так называемых крутильных весов:
q
q
Кулон определил зависимость силы от
взаимодействия заряженных тел величины заряда
q и от расстояния между их центрами R.
Шарль Огюсте́н де Куло́н
(1736 – 1806)
8.
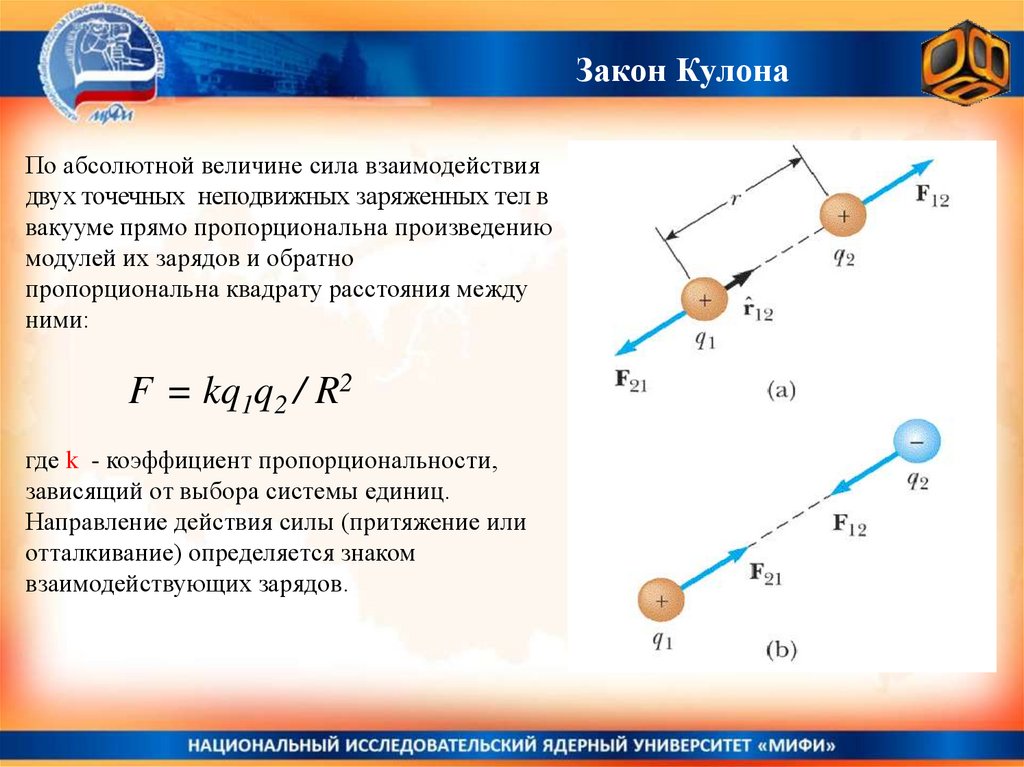
Закон КулонаПо абсолютной величине сила взаимодействия
двух точечных неподвижных заряженных тел в
вакууме прямо пропорциональна произведению
модулей их зарядов и обратно
пропорциональна квадрату расстояния между
ними:
F = kq1q2 / R2
где k - коэффициент пропорциональности,
зависящий от выбора системы единиц.
Направление действия силы (притяжение или
отталкивание) определяется знаком
взаимодействующих зарядов.
9.
Закон Кулона. Единицы измерения заряда.В системе СИ коэффициент k численно
равен силе взаимодействия двух единичных
(1 Кулон) зарядов на единичном расстоянии
(1 метр) друг от друга.
q1q2
F k 2 ,
r
2
Нм
м
1
9
k
9 10
2
Кл
Ф
4 0
0 0,885 10 11 Ф м
В Гауссовой системе коэффициент k
= 1, а электрический заряд измеряется в
ед. Гаусс = [н1/2м] = [кг1/2м3/2/с] =~ 1,05*10-5 Кл = 10,5 мкКл
Два заряда по 10,5мкКл на расстоянии 1 м взаимодействуют с силой 1 Н.
10.
Потенциальная энергия взаимодействияэлектрических зарядов.
Закон Кулона
F = kq1q2 / R2
математически очень похож на закон гравитационного взаимодействия
F = Gm1m2 / R2
Потенциальная энергия взаимодействующих электрических зарядов тоже определяется
формулой, похожей на формулу потенциальной энергии гравитационного
взаимодействия (Wгр =
q2
- Gm1m2 / R).
Wэл = kq1q2 / R
величины зарядов в этой формуле - алгебраические. При
одинаковых знаках зарядов потенциальная энергия
взаимодействия зарядов положительна, при разных знаках отрицательна.
R
q1
11.
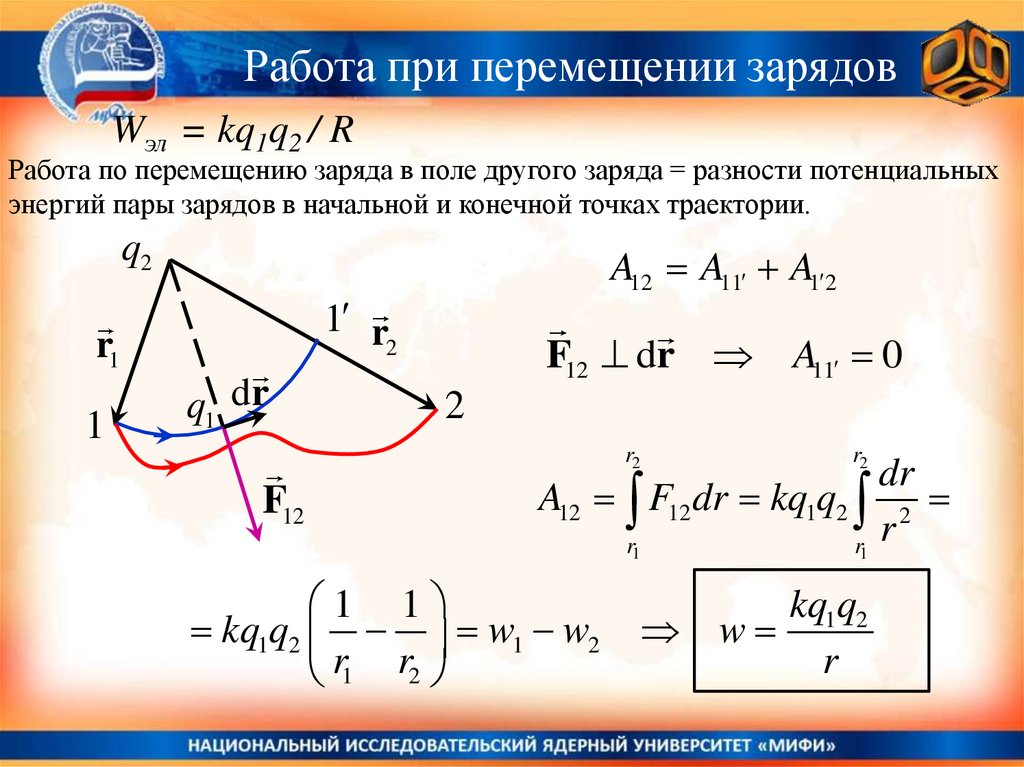
Работа при перемещении зарядовWэл = kq1q2 / R
Работа по перемещению заряда в поле другого заряда = разности потенциальных
энергий пары зарядов в начальной и конечной точках траектории.
q2
1 r
2
r1
1
A12 A11 A1 2
q1 dr
F12 dr A11 0
2
r2
F12
r2
dr
A12 F12 dr kq1q2 2
r
r1
r1
1 1
kq1q2 w1 w2
r1 r2
kq1q2
w
r
12.
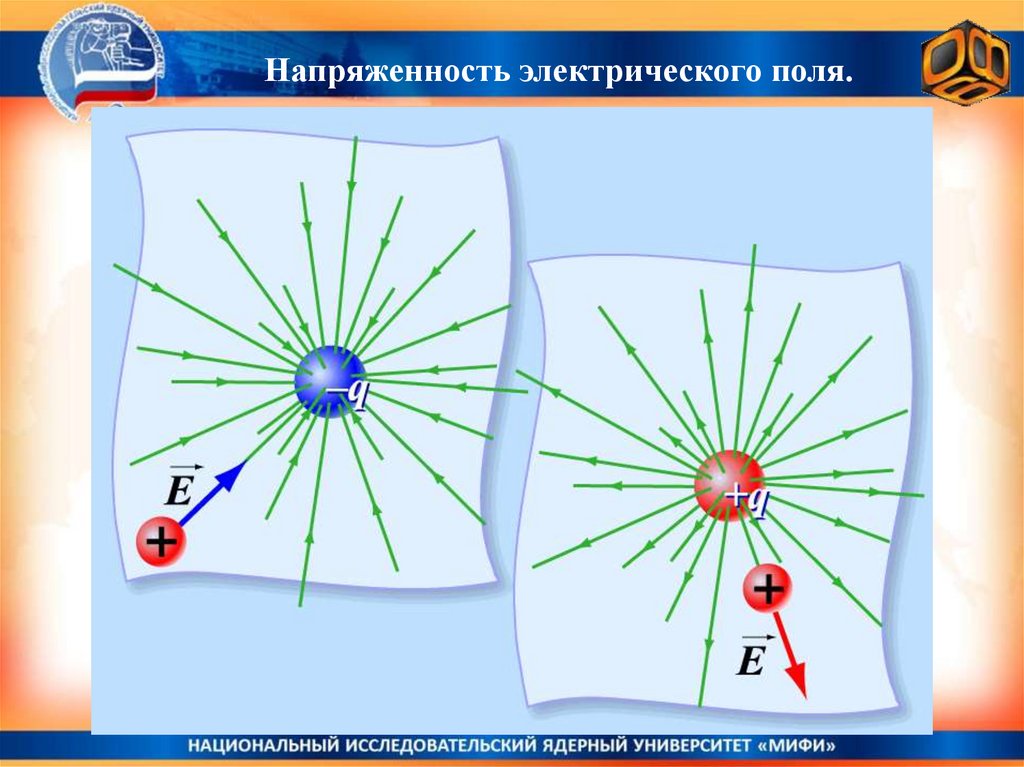
Электрическое поле.Взаимодействия удаленных тел осуществляются с помощью некоторого
промежуточного агента. Таким “агентом” может быть т. н. “поле сил”.
q
Q
Считается, что электрические заряды создают во всем
окружающем пространстве “электрическое поле сил”, которое
и действует на другие заряды.
Электрическое поле - особая форма материи.
Элекрическое поле можно наглядно изобразить в виде
картины “силовых линий”. В любой точке, куда помещен
другой - “пробный” - положительный заряд q, сила,
действующая на него со стороны поля заряда Q, будет
направлена вдоль этих линий.
Для точечного заряда силовые линии радиально расходятся
(если Q>0) из точки заряда или сходятся к ней (если Q<0).
13.
Напряженность электрического поля.В любой точке, куда будет помещен другой - “пробный” - заряд q, сила, действующая
на него со стороны поля заряда Q, пропорциональна величине “пробного” заряда
(Закон Кулона: F
= kQq / R2 ).
Величина, равная отношению силы, действующей на
“пробный” заряд q, к величине “пробного” заряда,
характеризует поле, создававемое зарядом Q, и называется
напряженностью электрического поля.
q
Q
Е = kQ / R2
Напряженность Е - это векторная величина, по направлению
совпадающая с направлением действия силы на пробный
положительный заряд
F r qE r
“Густота” силовых линий пропорциональна величине напряженности электрического
поля.
14.
Напряженность электрического поля.15.
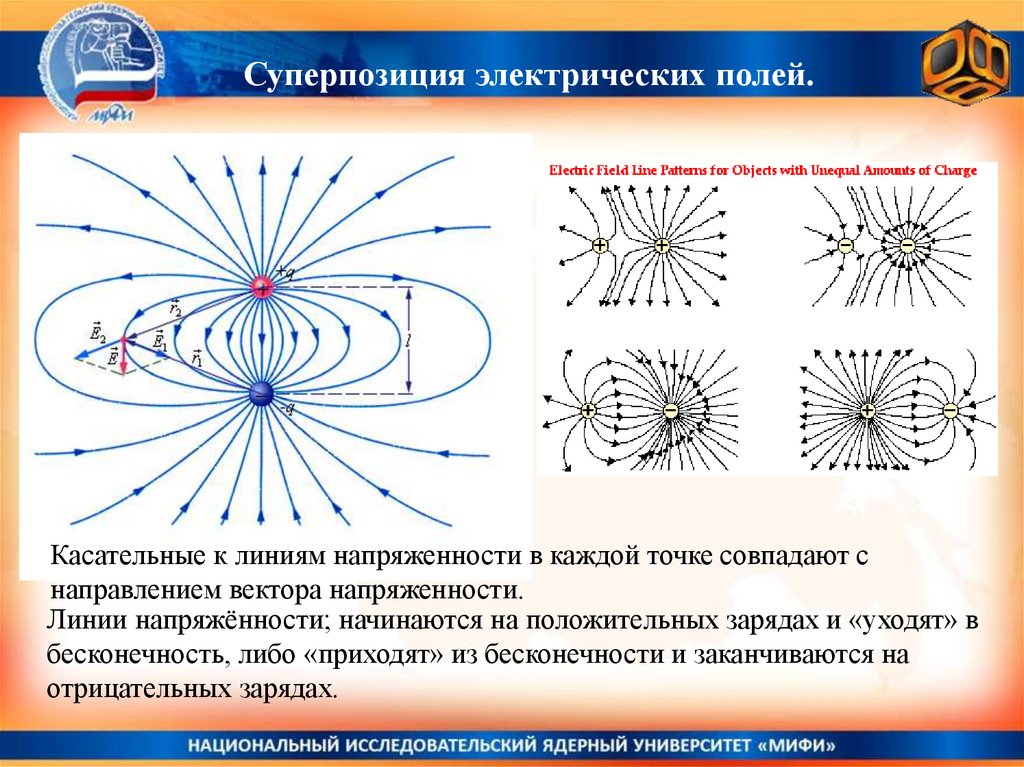
Суперпозиция электрических полей.Если на тело действуют несколько разных сил, то по законам механики
результирующая сила равна геометрической сумме всех действующих сил:
Fрез = F1 + F2 + F3 + ...
Q1>0
Q2<0
Ерез = Е1 + Е2 + Е3 + ...
Е2
Е1
Если в данной точке пространства электрические поля
создаются несколькими зарядами, суммарная напряженность
электрического поля в этой точке будет равна их векторной
сумме:
Ерез
16.
Суперпозиция электрических полей.Касательные к линиям напряженности в каждой точке совпадают с
направлением вектора напряженности.
Линии напряжённости; начинаются на положительных зарядах и «уходят» в
бесконечность, либо «приходят» из бесконечности и заканчиваются на
отрицательных зарядах.
17.
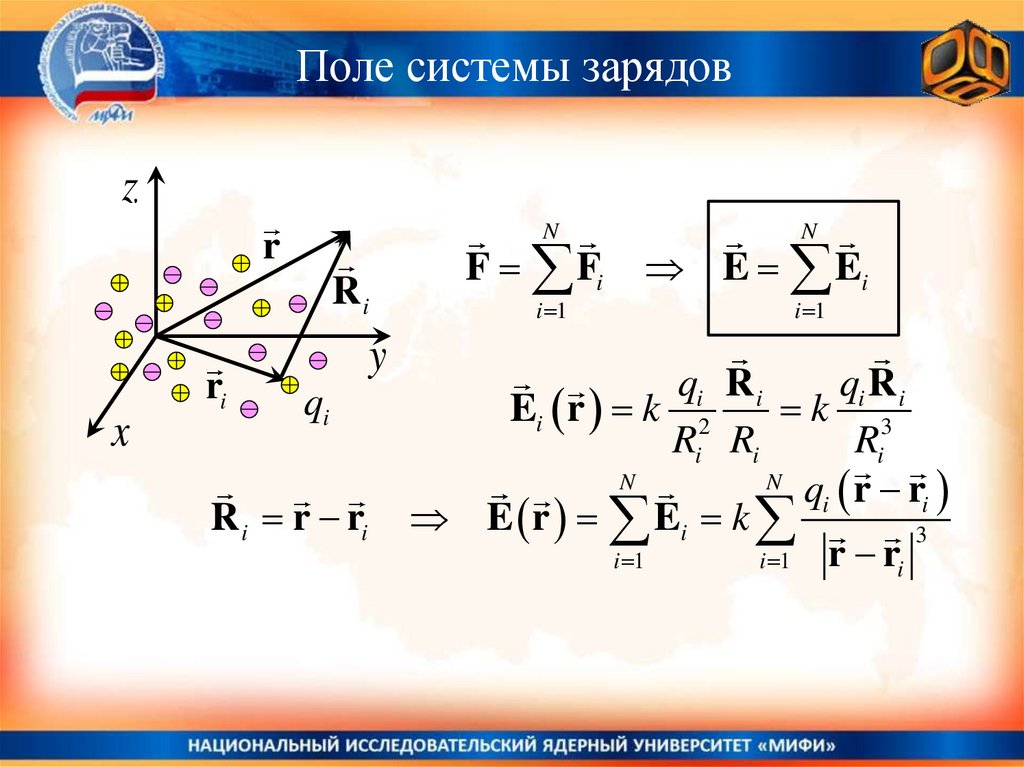
Поле системы зарядовz
N
r
Ri
ri
x
y
qi
R i r ri
F Fi
i 1
N
E Ei
i 1
qi R i
qi R i
Ei r k 2
k 3
Ri Ri
Ri
N
N
qi r ri
E r Ei k
3
r ri
i 1
i 1
18.
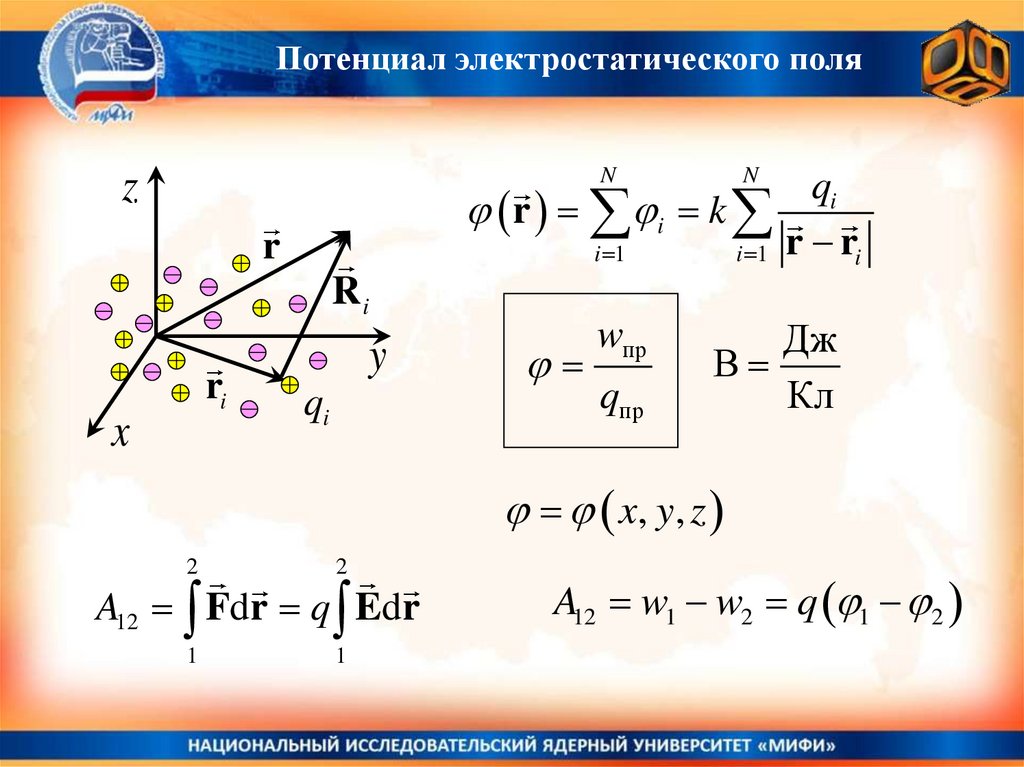
Потенциал электростатического поляz
N
N
i 1
i 1
r i k
r
Ri
ri
x
y
qi
wпр
qпр
qi
r ri
Дж
В
Кл
x, y , z
2
2
1
1
A12 Fdr q Edr
A12 w1 w2 q 1 2
19.
Напряжённость и потенциалСвязь между напряжённостью электрического
поля и потенциалом
F w qE q
E
Ex
, Ey
, Ez
x
y
z
2
2
1
1
A12 q 1 2 q Edr 1 2 Edr
20.
Поле системы зарядовПотенциальная энергия взаимодействия
N
kqn
1 N N
1 N N kqi qn 1 N
w win
qi
2 i 1 n 1
2 i 1 n 1 rin
2 i 1 n 1 rin
n i
1 N
w qi i
2 i 1
n i
i
n i
N
n 1
n i
kqn
rin
21.
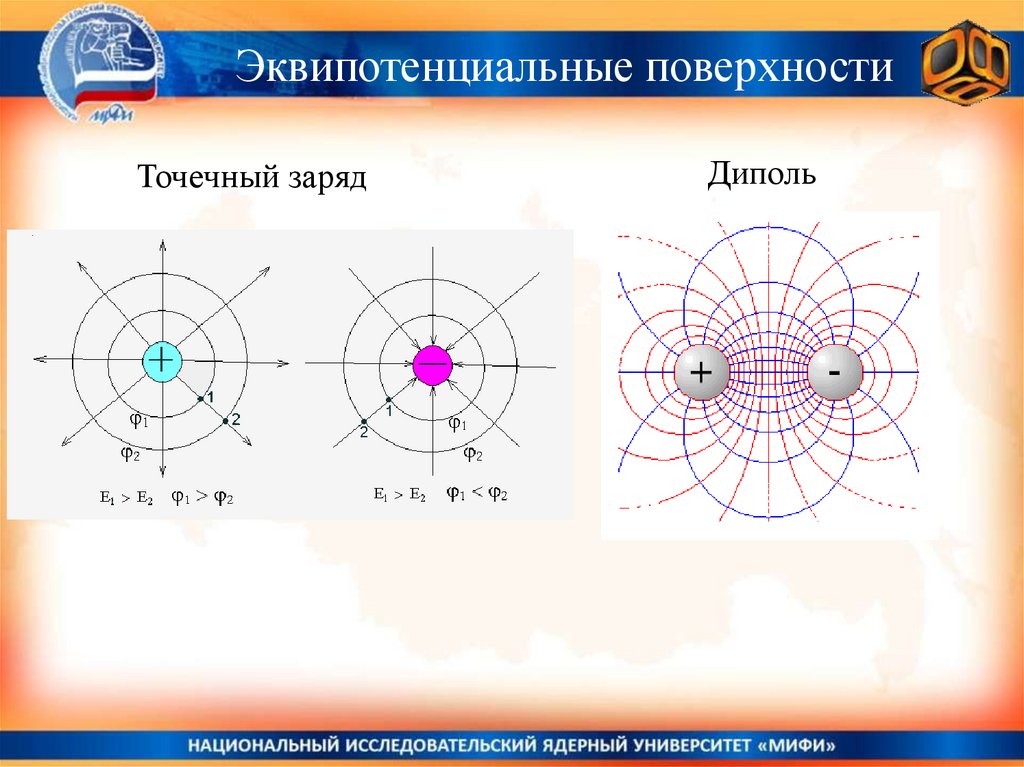
Эквипотенциальные поверхности и линииПоверхности, на которых потенциал принимает постоянное
значение, называются эквипотенциальными поверхностями.
x, y, z const
Линии напряжённости и эквипотенциальные поверхности
одного и того же поля пересекаются друг с другом под
прямыми углами.
22.
Эквипотенциальные поверхностиТочечный заряд
Диполь
23.
Курс общей физики НИЯУ МИФИСпасибо за внимание!
Следующая лекция
15 сентября
24.
Курс общей физики НИЯУ МИФИЛекция 2
• Электрическое поле точечного диполя.
• Диполь во внешнем электрическом поле
• Поле системы зарядов на больших
расстояниях.
• Пример решения задач
25.
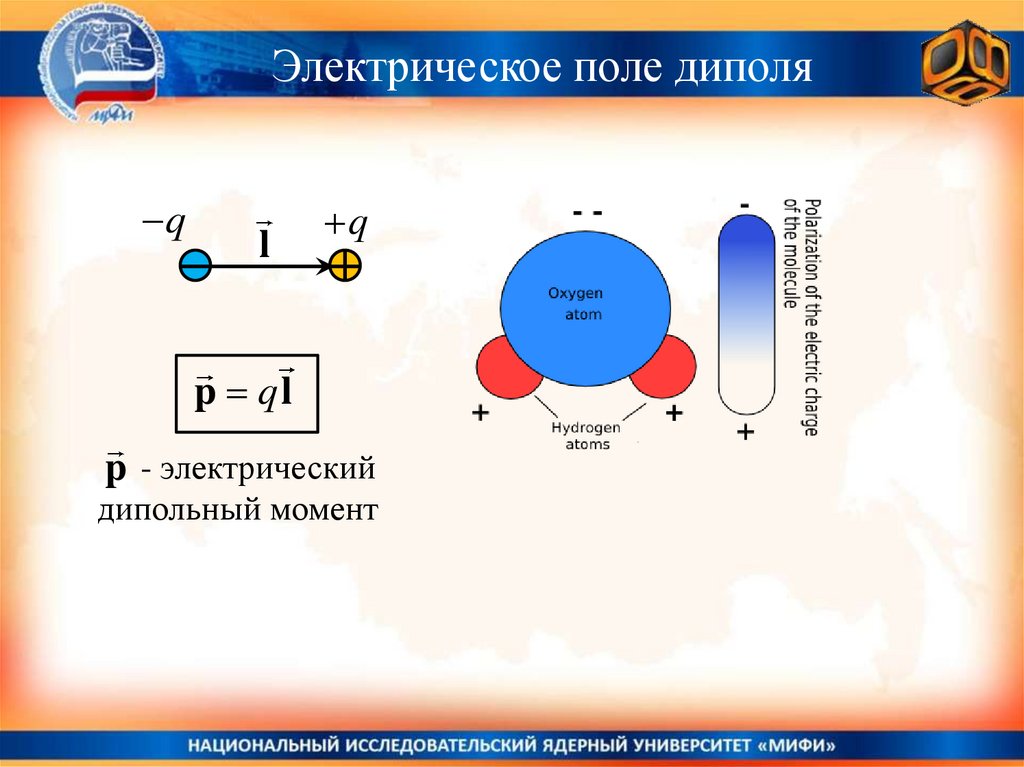
Электрическое поле диполяq
l
q
p ql
p - электрический
дипольный момент
26.
Немного математикиПриращение и дифференциал функции трёх переменных
f
f
f
f f r dr f r df dx dy dz
x
y
z
f f f
f , , dr dx, dy , dz
x y z
df f dr
27.
Электрическое поле диполяdf f dr
r
q
r
=
- т r l
+ т r т l
kq r
r
Eт l 2 l k 3 q l
r r
r
l
l
A
kq
kq
д r
r r l
r l
q
kq
т r т r
r
r p
д k 3
r
p ql
28.
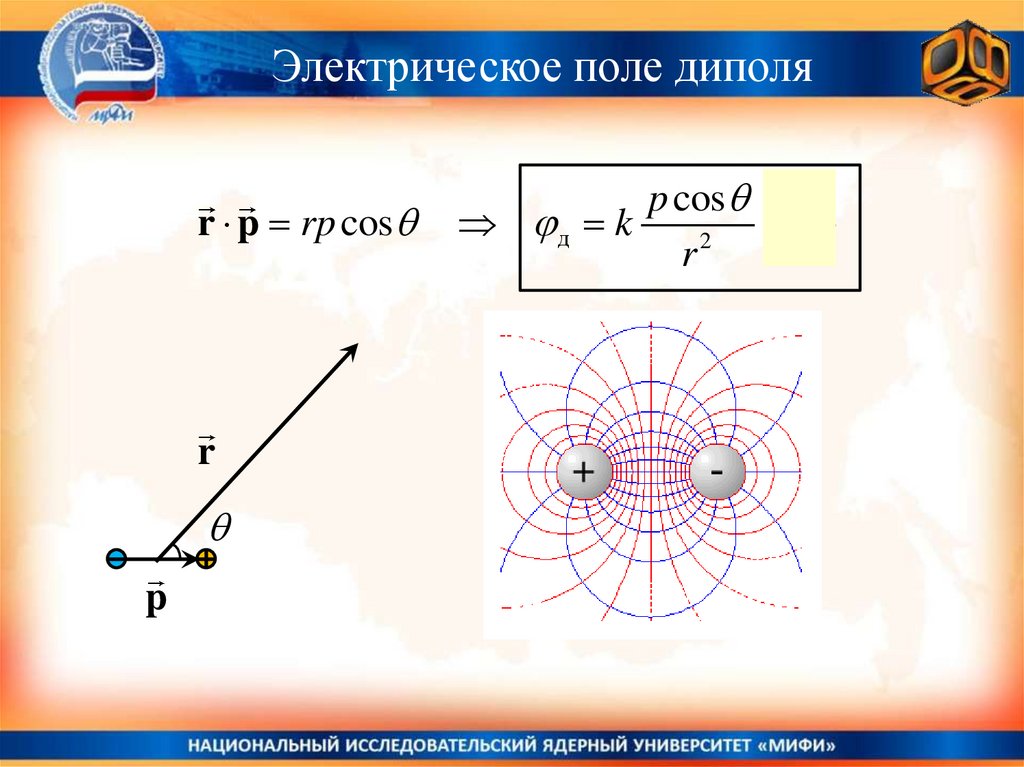
Электрическое поле диполяr p rp cos
r
p
p cos
д k
r2
1
r2
29.
Электрическое поле диполяНапряжённость электрического поля диполя
r p
1
Eд д k 3 k r p 3
1
r p
3
r
r r
df r
1
3 r
3r
Математическое
f r
3 4 5
дополнение.
dr r
r
r r
r
r p xp x yp y zpz xp x yp y zp z e x ...
x
px e x p y e y pz e z p
1
k 3 r p r
Eд 3
p
2
3
r r
r
30.
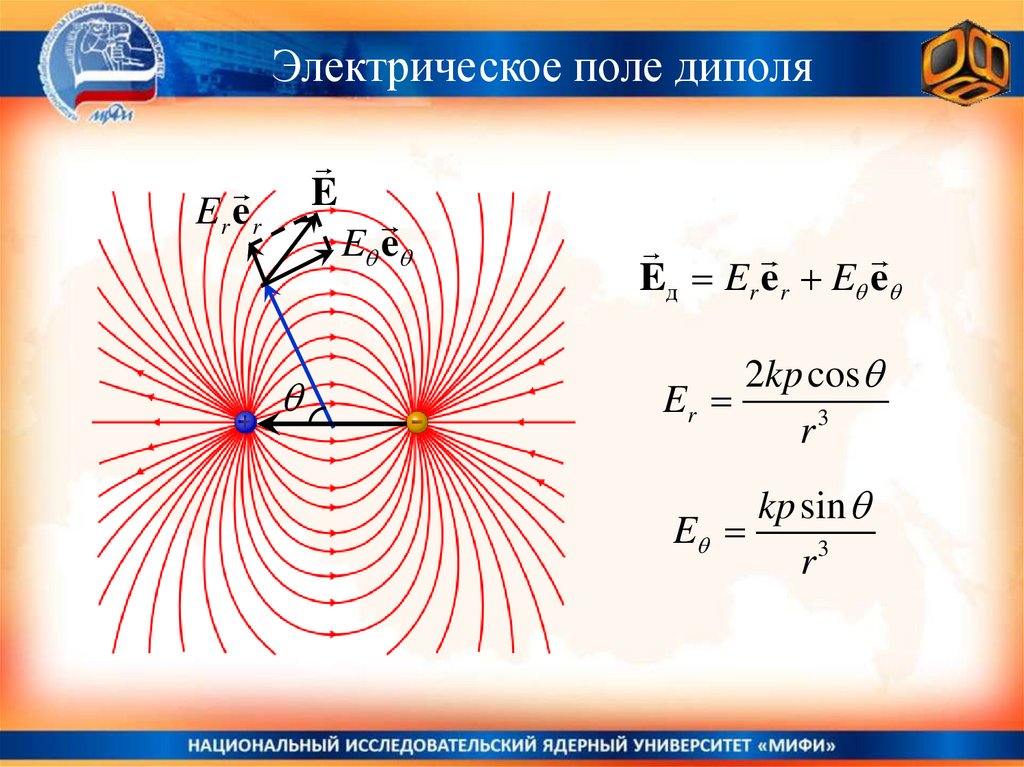
Электрическое поле диполяE
Er e r
E e
Eд Er e r E e
2kp cos
Er
r3
kp sin
E
r3
31.
Курс общей физики НИЯУ МИФИСпасибо за внимание!
Следующая лекция
15 сентября
32.
Диполь в электрическом полеПотенциальная энергия диполя
во внешнем электрическом поле
E
F
r
o
l
F
M
r l
w q r l q r
q r l r
q l p E
p q l , E
w p E pE cos
33.
Диполь в электрическом полеМомент сил, действующих на диполь
во внешнем электрическом поле
E
F
r
o
l
F
M
r l
E r l E r F F
l sin - плечо пары сил
M F l sin qEl sin pE sin
E
p
M
M p E
34.
Диполь в электрическом полеМатематическое дополнение. Приращение и
дифференциал векторной функции трёх переменных
f fx , f y , fz
f x f x r dr f x r df x
dr f x dr f x ,
dr dx dy dz
x
y
z
f
f
f
df dr f dx dy dz
x
y
z
35.
Диполь в электрическом полеСила, действующая на диполь
во внешнем электрическом поле
F F F qE r l qE r
E
F
q l E q l E p E
F
l
E
E
E
F p E px
py
pz
r l
x
y
z
r
o
df dr f
Замечание: В статическом
электрическом поле
F w p E
36.
Диполь в электрическом полеПример 1. Однородное электрическое поле
E const F 0
Пример 2. Слабо неоднородное электрическое поле
E E x ex
E
p px
Fx px
x
x
Ex
px 0,
0 Fx 0
x
37.
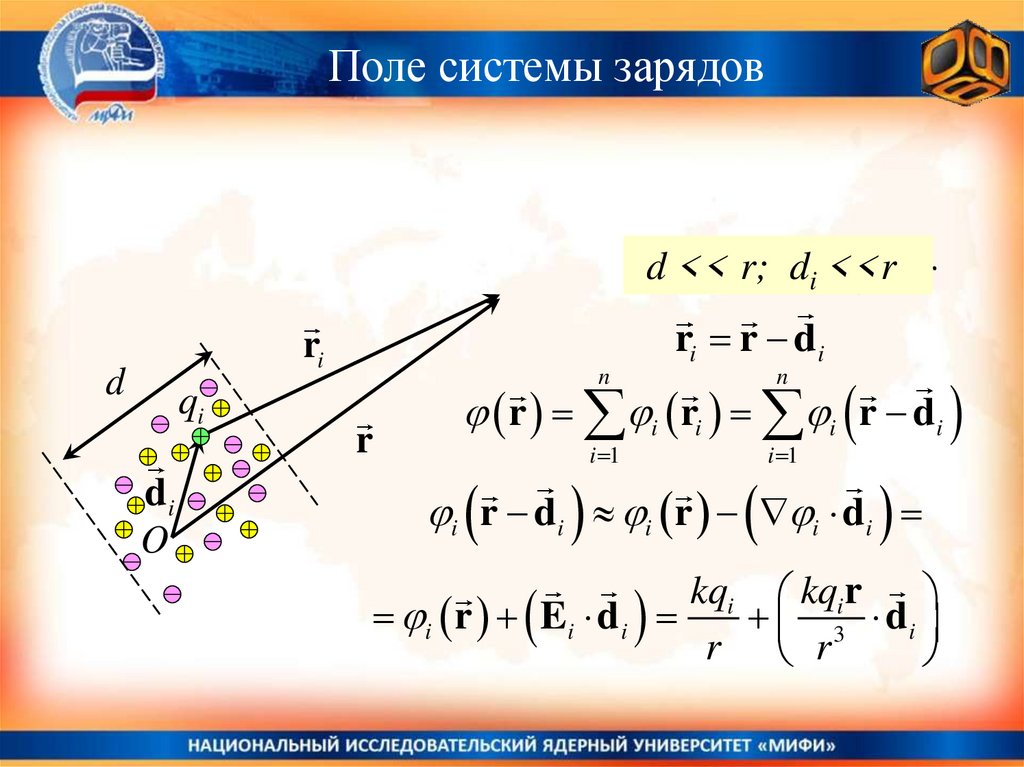
Поле системы зарядовdd <<
r r; di <<r
di r
ri r di
ri
d
qi
di
O
r
r i ri i r di
n
n
i 1
i 1
i r di i r i di
kqi kqir
i r Ei d i
3 di
r r
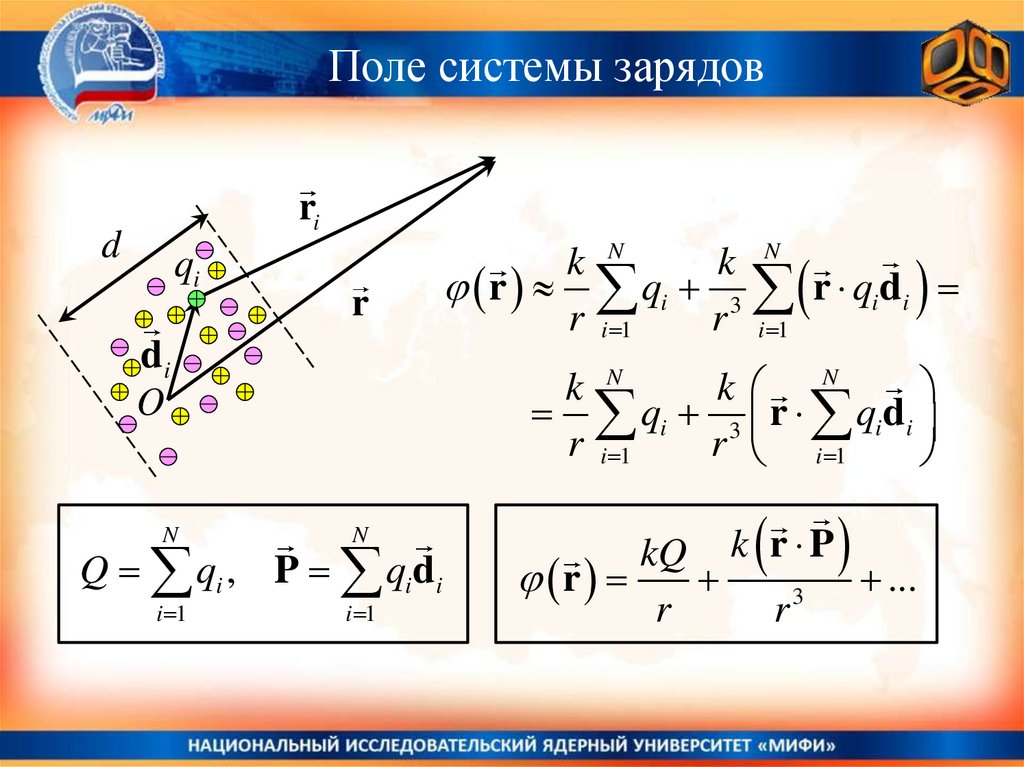
38.
Поле системы зарядовri
d
qi
r
di
O
k N
k N
r qi 3 r qidi
r i 1
r i 1
k N
k N
qi 3 r qidi
r i 1
r i 1
N
N
i 1
i 1
Q qi , P qidi
kQ k r P
r
...
3
r
r
39.
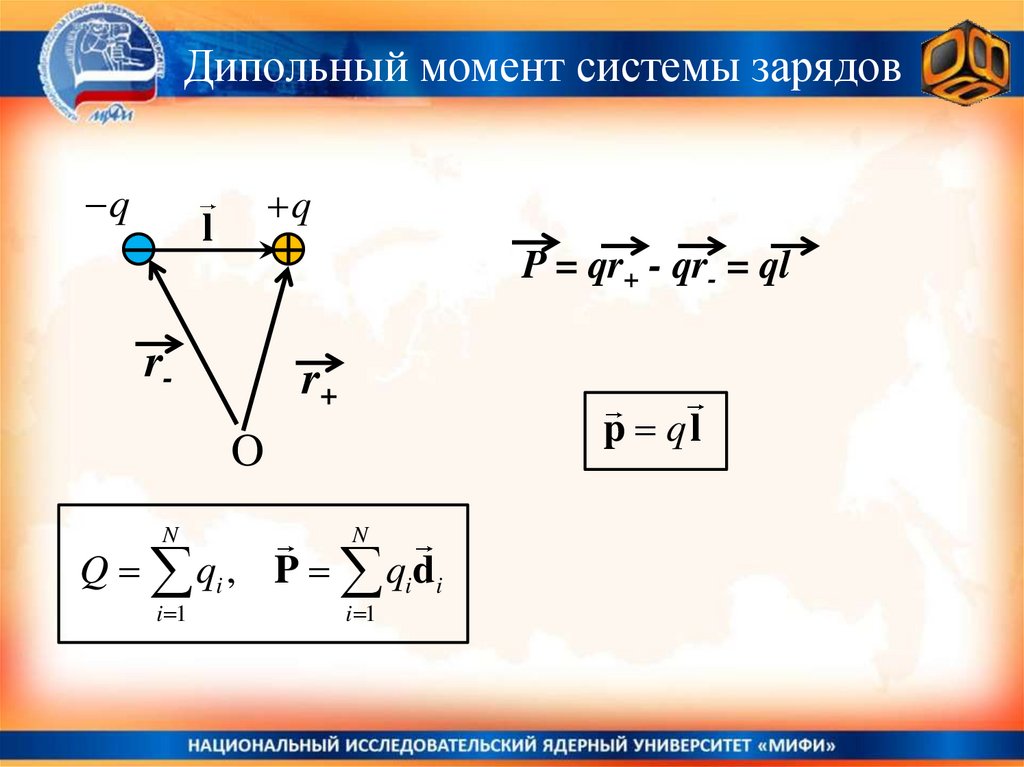
Дипольный момент системы зарядовq
q
l
P = qr+ - qr- = ql
r-
r+
p ql
O
N
N
i 1
i 1
Q qi , P qidi
40.
Курс общей физики НИЯУ МИФИСпасибо за внимание!
Следующая лекция
15 сентября


























 physics
physics








