Электростатическое поле в вакууме

1.

Электростатическое поле в вакууме
Электрический заряд
Свойства:
1. Электрический заряд – инвариантная величина (по определению)
2. Существует два вида заряда: “+” и ‘”–”
3. Заряд – дискретная величина: q n | e |
4. Выполняется закон сохранения заряда:
В любой электрически изолированной системе алгебраическая
сумма зарядов не изменяется

2.

Электростатическое поле в вакууме
Закон Кулона
F12
+
1
+
1
+
2
F12
F21
F21
1 q1 q2 r12
F12
4 0 r122 r12
2
1 4 0 10 7 c 2 9 109 м/Ф
c – скорость света

3.

Электростатическое поле в вакууме
Электрическое поле
F
q
Всякий электрический заряд q изменяет
свойства окружающего его пространства –
создает электрическое поле.
Это поле проявляет себя в том, что помещенный
в какую-либо его точку другой, “пробный”,
заряд испытывает действие силы.
E
F
q
E – напряженность электрического поля

4.

Электростатическое поле в вакууме
Напряженность поля точечного заряда
Закон Кулона в полевой форме
F
1 q r
E
4 0 r 2 r
q
F q E

5.

Электростатическое поле в вакууме
Принцип суперпозиции
Напряженность поля точечных зарядов равна сумме напряженностей
полей отдельных зарядов.
1
E Ei
4 0
qi ri
r2 r
i
i

6.

Электростатическое поле в вакууме
Распределение зарядов
dq
dV
dq
dS
dq
dl
dq
dV
объемная плотность заряда
dq
dS
поверхностная плотность заряда
dq
dl
линейная плотность заряда

7.

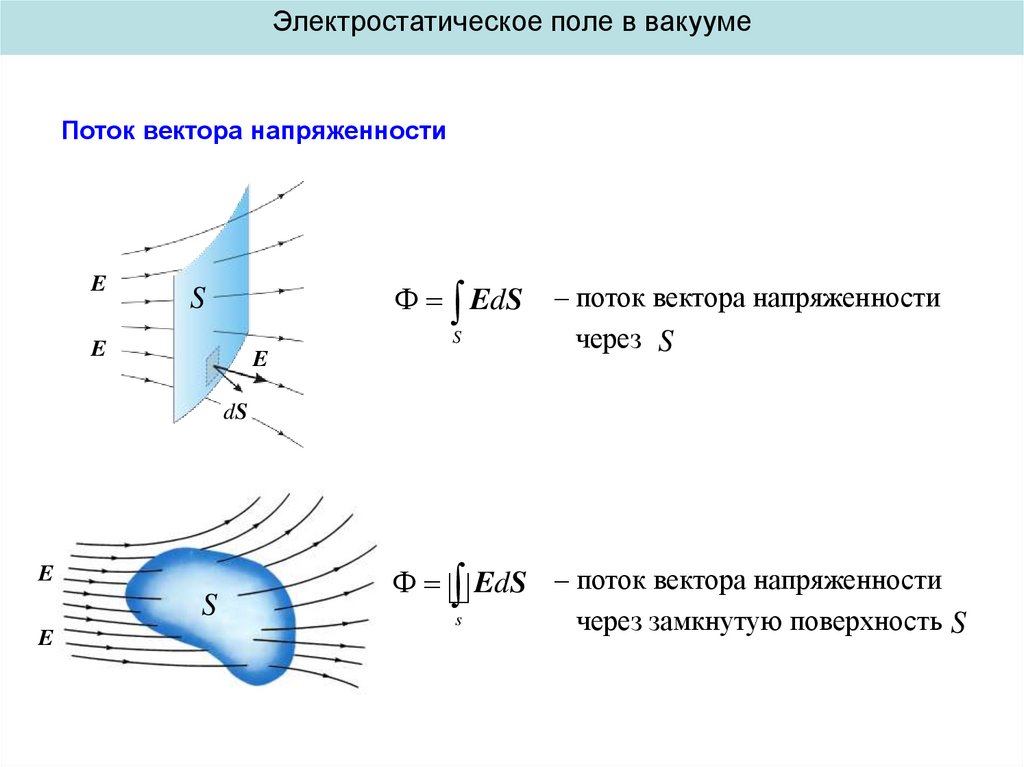
Электростатическое поле в вакууме
Поток вектора напряженности
n
d EdS EdS cos
E
d – поток вектора напряженности через dS
dS
dS ndS – векторный элемент поверхности

8.

Электростатическое поле в вакууме
Поток вектора напряженности
E
EdS
S
S
E
E
– поток вектора напряженности
через S
dS
E
S
E
EdS
s
– поток вектора напряженности
через замкнутую поверхность S

9.

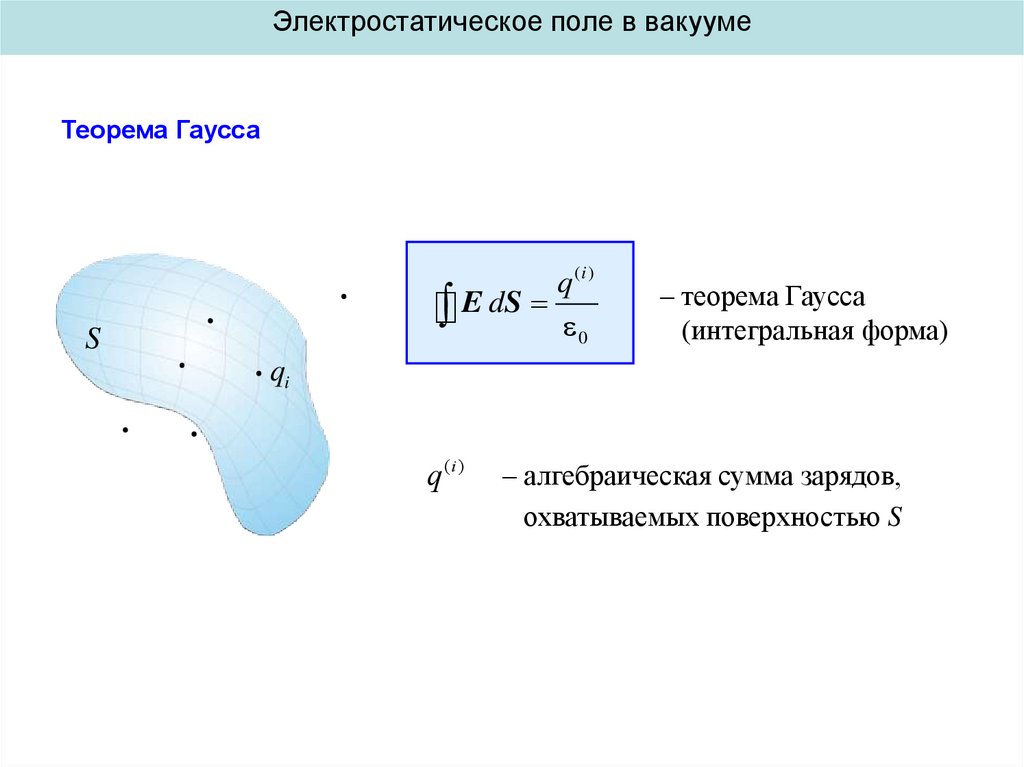
Электростатическое поле в вакууме
Теорема Гаусса
S
q (i )
E dS
0
– теорема Гаусса
(интегральная форма)
qi
q (i )
– алгебраическая сумма зарядов,
охватываемых поверхностью S

10.

Электростатическое поле в вакууме
Теорема Гаусса
1
V
1)
1 q (i )
E dS
0 V
1
lim
V 0 V
EdS divE
– дивергенция вектора E
q( i )
2) lim
V 0 V
div E 0
– теорема Гаусса
(дифференциальная форма)

11.

Электростатическое поле в вакууме
Теорема Гаусса
В декартовой системе координат
x
y z
x
y
z
E
0
E x E y E z
div E
x
y
z
– дифференциальный оператор (набла),
где x, y, z – орты осей X, Y, Z
– теорема Гаусса
(дифференциальная форма)

12.

Электростатическое поле в вакууме
Применение теоремы Гаусса
1) Поле равномерно заряженной плоскости
ΕdS 2E S
S
2 E S S 0
E
q
E
E
2 0
q S

13.

Электростатическое поле в вакууме
Применение теоремы Гаусса
2) Поле двух параллельных плоскостей
E1
E1
E1
E2
E2
E2
E
0
E 0
1
E 0
2
E E1 E2
E
0

14.

Электростатическое поле в вакууме
Применение теоремы Гаусса
3) Поле равномерно заряженного цилиндра
ΕdS E 2 r l
E
l
r
2a
2 0 r
E 0
(r a)
(r a)
q l

15.

Электростатическое поле в вакууме
Применение теоремы Гаусса
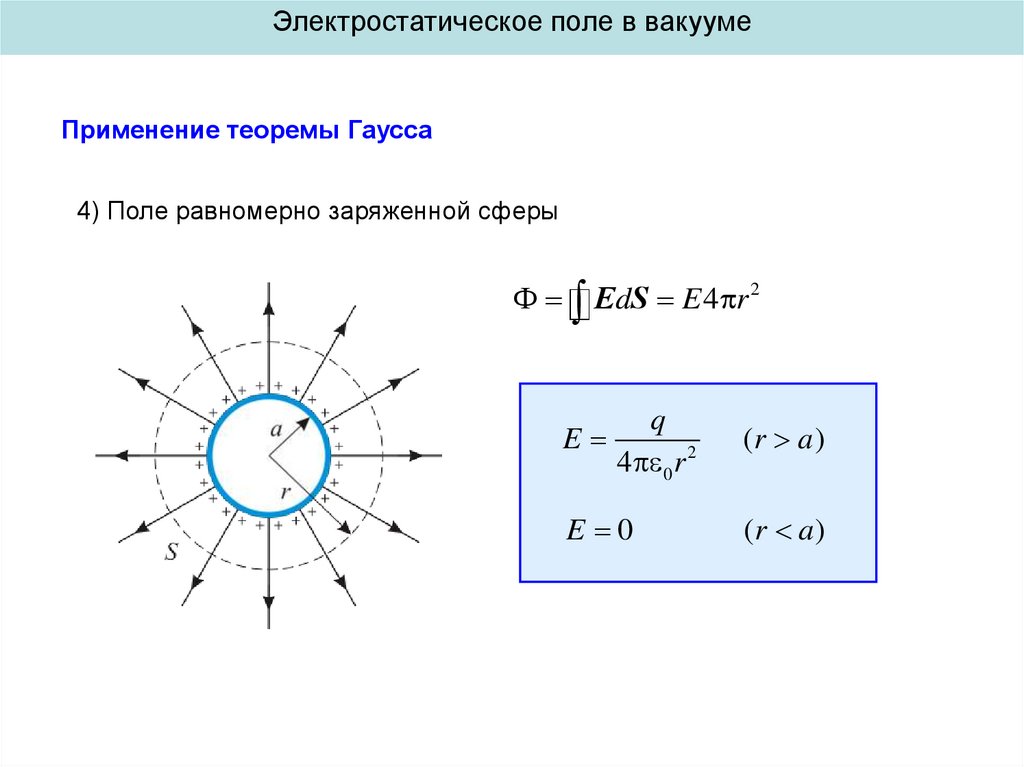
4) Поле равномерно заряженной сферы
2
Ε
d
S
E
4
r
E
q
4 0 r 2
E 0
(r a)
(r a)

16.

Электростатическое поле в вакууме
Теорема о циркуляции вектора E
2
A12 Edr – работа поля по перемещению q = 1
1
2
q
в поле точечного заряда q
2
2
q
rdr
q
rdr
q 1 1
A12
3
3
4 0 1 r
4 0 1 r
4 0 r1 r2
Если r1 = r2 , тогда
1
q
E dr 0
– теорема о циркуляции
(интегральная форма)

17.

Электростатическое поле в вакууме
Теорема о циркуляции вектора E
Таким образом, электростатическое поле – потенциальное поле
1
S
Edr 0
n
1
lim
S 0 S
Edr (rot E ) n
ротор
S
rot E

18.

Электростатическое поле в вакууме
Теорема о циркуляции вектора E
rot E E
rot E 0
x
y
z
x
Ex
y
Ey
z
Ez
в декартовой
системе координат
– теорема о циркуляции
(дифференциальная форма)

19.

Электростатическое поле в вакууме
Потенциал
2
Определение потенциала:
1 2 Edr
1
Потенциал – это потенциальная энергия q = 1
U
q
, где U – потенциальная энергия заряда q
в электрическом поле

20.

Электростатическое поле в вакууме
Потенциал поля точечного заряда
Для поля точечного заряда (см. слайд 1):
q 1 1
1 2
4 0 r1 r2
r2
2 0 (нормировка)
1 q
4 0 r
– потенциал поля точечного заряда

21.

Электростатическое поле в вакууме
Потенциал поля системы зарядов
Из принципа суперпозиции для напряженности электрического поля
E Ei
следует принцип суперпозиции для потенциала
i
qi
1
r
4 0
i
Объемное распределение заряда:
1
dV
4 0 r

22.

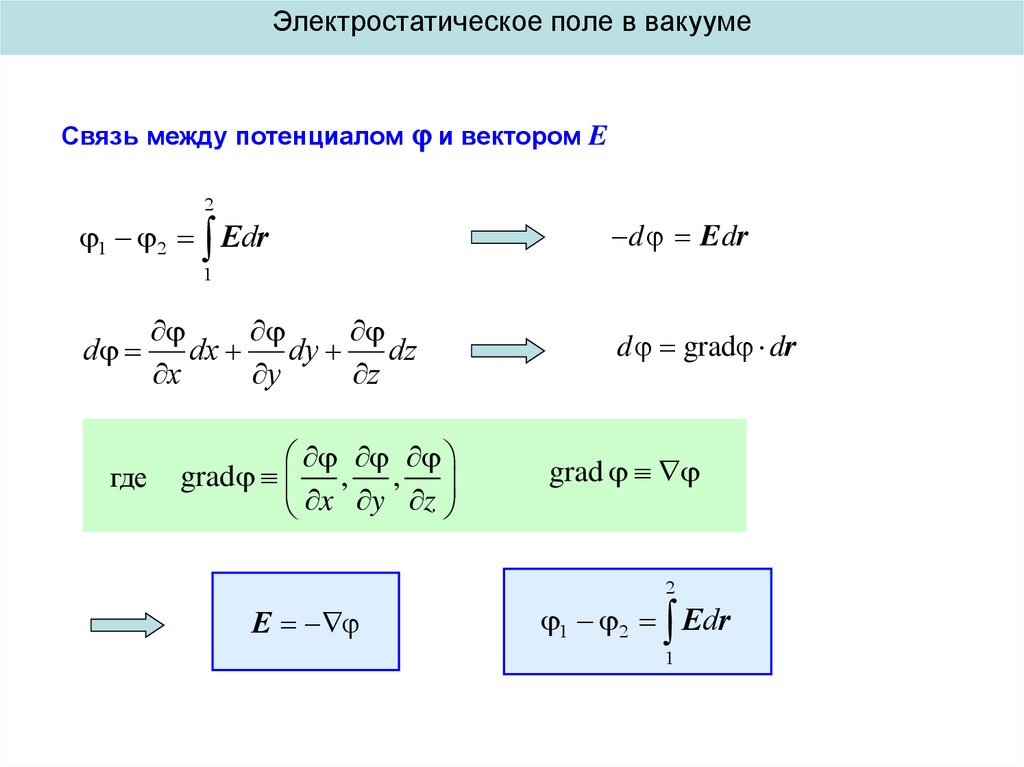
Электростатическое поле в вакууме
Связь между потенциалом
и вектором E
2
1 2 Edr
d E dr
d
dx
dy
dz
x
y
z
d grad dr
1
где
grad , ,
x y z
grad
2
E
1 2 Edr
1