Similar presentations:
Электричество и магнетизм. Теорема Гаусса в дифференциальной форме. (Лекция 3)
1. Электричество и магнетизм
Лекция 3.2. ТЕОРЕМА ГАУССА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
• Замечательное свойство электрического поля, которое выражаетсобой теорема Гаусса, побуждает представить эту теорему в иной
форме, расширяющей ее возможности как инструмента
исследования и расчета.
• В отличие от формы (2.05) —ее называют интегральной — мы
будем искать дифференциальную форму теоремы Гаусса, в
которой устанавливается связь между объемной плотностью
заряда и изменениями напряженности Е в окрестности данной
точки пространства.
3.
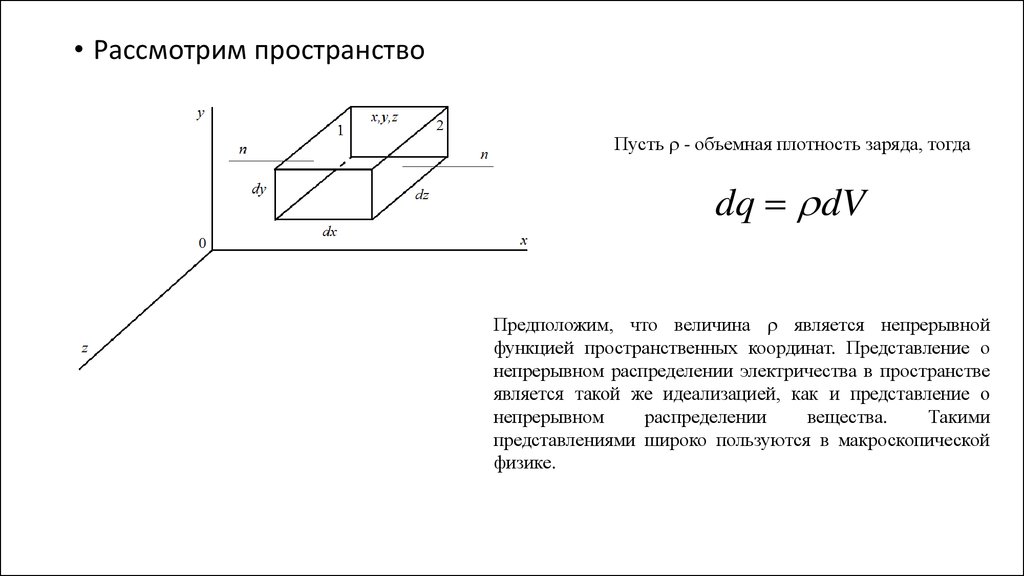
• Рассмотрим пространствоПусть - объемная плотность заряда, тогда
dq dV
Предположим, что величина является непрерывной
функцией пространственных координат. Представление о
непрерывном распределении электричества в пространстве
является такой же идеализацией, как и представление о
непрерывном
распределении
вещества.
Такими
представлениями широко пользуются в макроскопической
физике.
4.
• Возьмем в пространстве бесконечно малый прямоугольный параллелепипедсо сторонами dx, dy, dz, параллельными координатным осям прямоугольной
системы координат (рис. 3.015). На грани 1 внешняя нормаль направлена в
отрицательную сторону оси X. Поэтому поток вектора Е через эту грань будет
Ex( x)dydz
На противоположной грани 2, наоборот, направление внешней нормали
совпадает с положительным направлением оси x, и для потока через эту грань
следует писать
Ex( x dx)dydz
5.
• Сумма обоих потоков будетEx ( x dx)dydz Ex ( x)dydz ( Ex ( x dx) Ex ( x))dydz
Ex
Ex
Ex dydz
dxdydz
dV
x
x
Ex
x
dV
x
где dV dxdydz
- объем параллелепипеда.
Аналогично найдутся потоки через две пары остальных граней.
y
E y
y
dV
Ez
z
dV
z
6.
• Полный поток через всю поверхность параллелепипеда:Ey
Ex
Ez
d x y z
dV
dV
dV
x
y
z
Ex E y Ez
d
dV
y
z
x
Ex Ey Ez
div( E )
y
z
x
d div( E )dV
(3.01)
7.
• По теореме Гаусса тот же поток равенd
dV
0 0
dq
Приравнивая оба выражения, получим
div( E )dV dV
0
div( E )
0
(3.02)
Эта
формула
и
выражает
электростатическую теорему Гаусса в
дифференциальной форме.
8.
• Часто для описания вводят так называемы оператор набла , которыйв Декартовой системе координат имеет вид
i
j
k
x
y
z
E iEx jE y kEz
E x Ex y E y z Ez Ex E y Ez
x
y
z
E
0
(3.03)
Величина, определяемая выражением (3.02) или (3.03), сохраняет смысл независимо от
конкретной физической или геометрической природы вектора Е. Она называется
дивергенцией вектора Е. С дивергенцией приходится встречаться в самых разнообразных
вопросах математики и физики, чем и оправдывается введение этого математического
понятия.
9.
• Теорема Гаусса в дифференциальной форме является следствием тойже теоремы в интегральной форме. Обращая порядок рассуждений,
легко убедиться, что из дифференциальной формы теоремы Гаусса
можно получить интегральную.
• Обе формы математически эквивалентны, но дифференциальная
форма имеет смысл лишь в том случае, когда электричество
распределено в пространстве с конечной плотностью . Если
обращается в бесконечность в отдельных точках, на линиях или
поверхностях,
то
дифференциальная
форма
становится
неприменимой, тогда как интегральная форма применима и в таких
случаях.
• В этом смысле интегральная форма обладает большей
математической общностью, чем дифференциальная. Однако
разрывные распределения электричества с бесконечно большими
значениями являются математическими абстракциями и в физике
должны рассматриваться как предельные случаи непрерывных
распределений с всюду конечными значениями .
• Если это иметь в виду, то можно утверждать, что интегральная и
дифференциальная
формы
теоремы
Гаусса
полностью
эквивалентны.
10. Работа сил электрического поля.
• Работа, совершаемая силой по перемещению тел, определяетсяследующим образом
A Fr
(3.04)
где вектор F – сила, действующая на тело, а вектор r – перемещение. В случае
электрических зарядов
A Fк r
где вектор Fк – сила взаимодействия зарядов.
11.
• Рассмотрим работу по перемещению заряда q в поле заряда QВ случае закона Кулона, выражение для работы
принимает вид
dA Fк dr
1
qq '
dA
rdr
3
4 0 r
(3.05)
Работа по перемещению заряда из точки 1 в точку 2
r2
r2
1 Qq
1 Qq
A
rdr
rdr
3
3
4 0 r
4 0 r
r1
r1
12.
r2Qq rdr
A
4 0 r1 r 3
При
dr 0 rdr rdr
Qq rdr
Qq dr
Qq 1 1
A
3
2
4 0 r1 r
4 0 r1 r
4 0 r1 r2
r2
• Таким образом
r2
Qq 1 1
A
4 0 r1 r2
(3.06)
Из выражения (3.06) следует, что работа сил электрического поля не зависит от
траектории движения, а зависит только от начального и конечного положения заряда q.
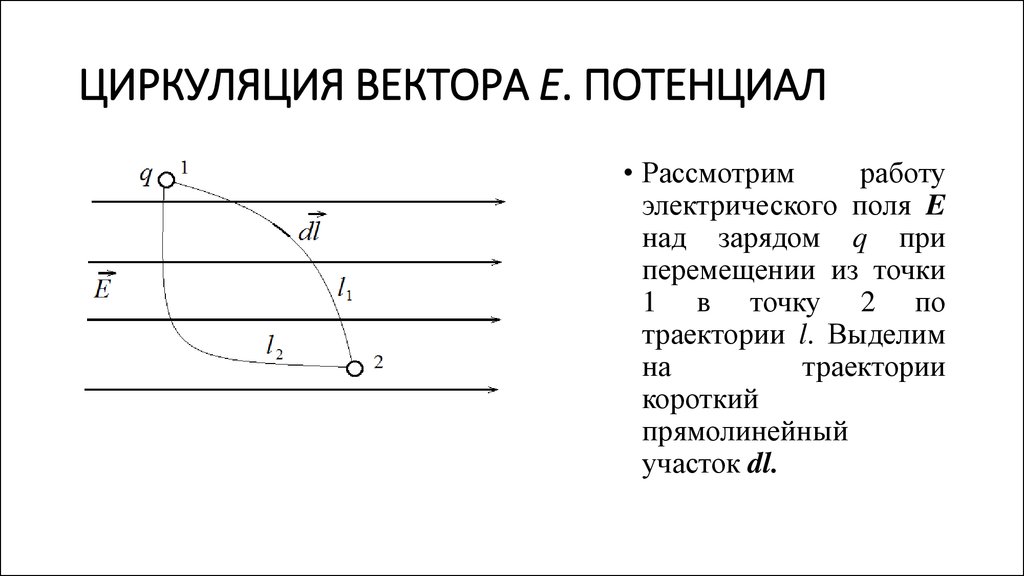
13. ЦИРКУЛЯЦИЯ ВЕКТОРА Е. ПОТЕНЦИАЛ
• Рассмотримработу
электрического поля E
над зарядом q при
перемещении из точки
1 в точку 2 по
траектории l. Выделим
на
траектории
короткий
прямолинейный
участок dl.
14.
Работа поля на этом участке будет выражаться какdA qEdl
(3.07)
Предполагается, что в пределах участка dl поле остается однородным. Тогда работа
электрического поля по перемещению заряда из точки 1 в точку 2 будет выражаться
как
2
2
A qEdl q Edl
1
1
2
A q Edl
(3.08)
1
Этот интеграл берется по некоторой линии (пути), поэтому его называют линейным.
Попасть из точки 1 в точку 2 можно как по траектории l1 так по траектории l2.
15.
Теорема о циркуляции вектора Е утверждает, что работа сил электрического поляпо замкнутому контуру (замкнутой траектории) равна нулю.
A q Edl 0
l
Edl
0
(3.09)
l
Интеграл (3.09) по замкнутому пути называют циркуляцией вектора Е.
Таким базом, циркуляция вектора Е в любом электростатическом поле равна
нулю. Это утверждение и называют теоремой о циркуляции вектора Е.
16.
Доказательство теоремы.Разобьем произвольный замкнутый путь на две части l1 и l2. Так как работа не
зависит от траектории, то линейный интеграл
2
Edl
также не зависит от траектории.
1
Работа по замкнутому контуру будет равна
l1
l2
l1
l2
12
21
12
12
A q Edl Edl Edl Edl Edl 0
l
q Edl 0
l
Edl
l
0
что и требовалось доказать.
Поле, обладающее свойством
(3.09), называют потенциальным.
Подобными
свойствами
обладают электростатическое и
гравитационное поля, поэтому
эти
поля
называются
потенциальными.
17. Потенциал.
До сих пор мы рассматривали описание электрического поля с помощью вектораЕ. Существует, однако, и другой способ описания — с помощью потенциала, который
традиционно обозначается греческой буквой . Оба эти способа однозначно
соответствуют друг другу. Тот факт, что работа сил электрического поля не зависит от
траектории, а определяется только начальным и конечным положением (3.08) при
перемещении единичного положительного заряда из точки 1 в точку 2,
2
A q Edl
1
(3.08)
18.
позволяет утверждать, что в электрическом поле существует некоторая скалярнаяфункция координат (r), изменение с которой связано с работой
2
A q Edl q 1 q 2 q ( 1 2 )
1
2
1 2 Edl
(3.10)
1
где 1 и 2 — значения функции в точках 1 и 2. Так определенная величина (r)
называется потенциалом поля. Работа сил электрического поля определяется как
2
A q Edl q ( 2 1 ) q 2 q 1 q
(3.11)
1
где ∆ — разность потенциалов между точками 1 и 2.
19.
Выводы.Работа сил потенциального поля равна убыли потенциальной энергии частицы в поле
можно сказать, что потенциал — это величина, численно равная потенциальной
энергии единичного положительного заряда в данной точке поля.
Потенциалу какой-либо произвольной точки О поля можно условно приписать
любое значение 0 . Тогда потенциалы всех других точек поля определяются согласно
(3.10) однозначно. Если изменить 0 на некоторую величину d , то на такую же
величину изменятся и потенциалы во всех других точках поля.
Потенциал определяется с точностью до произвольной аддитивной постоянной.
Значение этой постоянной не играет роли, так как все электрические явления зависят
только от напряженности электрического поля. Последняя же определяется, как мы
увидим, не самим потенциалом в данной точке поля, а разностью потенциалов в
соседних точках поля. Единицей потенциала является вольт (В).
20.
Потенциал поля точечного заряда. Формула (3.10) содержит не только определениепотенциала , но и способ нахождения этой функции. Для этого достаточно вычислить
интеграл Еdl по любому пути между двумя точками и представить затем полученный
результат в виде убыли некоторой функции, которая и есть (r). Можно поступить и
проще. Воспользуемся тем, что формула (3.10) справедлива не только для конечных
перемещений, но и для элементарных dl. Тогда согласно этой формуле элементарная
убыль потенциала на этом перемещении есть
dA qEdl
(3.07)
dA qd
d Edl
(3.12)
21.
Другими словами, если известно поле Е(r), то для нахождения (r) надо представитьЕdl (путем соответствующих преобразований) как убыль некоторой функции. Эта
функция и есть (r).
Найдем таким способом потенциал поля неподвижного точечного заряда.
Известно, что поле точечного заряда описывается
выражением
q
E
e
4 0 r
q
q
d Edl
e dl
dr
2 r
2
4 0 r
4 0 r
где dr=erdl , тогда
q
d
dr d
const
2
4 0 r
4 0 r
q
2
22.
q4 0 r
const
Полагая, что при r 0, откуда следует что const=0. В итоге получаем
выражение для потенциала точечного заряда
q
4 0 r
(3.13)
23.
Потенциал поля системы зарядов.Пусть система состоит из неподвижных точечных зарядов q1, q2, q3 ... Согласно
принципу суперпозиции в любой точке поля напряженность Е=Е1+ Е2+Е3..., где Еi —
напряженность поля заряда qi . Тогда можно записать
Edl E1 E2 E3 ... dl E1dl E2 dl E3dl ...
1 2 3 ...
1 2 3 ... i
i
С учетом выражения для напряженности поля
точечного заряда, для потенциала получим
qi
4 0 i ri
1
(3.14)
24.
Потенциал при непрерывном распределении зарядов.Если заряды, образующие систему, распределены непрерывно, то, как обычно, мы
считаем, что каждый элементарный объем dV содержит «точечный» заряд dV, где —
объемная плотность заряда в месте нахождения объема dV. С учетом этого формуле
(3.14) можно придать иной вид:
1
4 0 V
dV
r
(3.15)
где интегрирование проводится или по всему пространству, или по той его
части, которая содержит заряды.
25.
Если заряды расположены только на поверхности S, то1
4 0
S
dS
r
(3.16)
где — поверхностная плотность заряда; dS — элемент поверхности S. Аналогичное
выражение будет и в том случае, когда заряды распределены линейно.
Итак, зная распределение зарядов (дискретное, непрерывное), мы можем в принципе
найти потенциал поля любой системы.
26. Связь между потенциалом и вектором Е
Электрическое поле, как известно, полностью описывается векторнойфункцией Е(r). Зная ее, мы можем найти силу, действующую на
интересующий нас заряд в любой точке поля, вычислить работу сил поля
при каком угодно перемещении заряда и др. А что дает введение
потенциала? Прежде всего, оказывается, зная потенциал (r) данного
электрического поля, можно достаточно просто восстановить и само поле
Е(r). Рассмотрим этот вопрос более подробно.
27.
d EdlВыделим
в
произвольной
точке
пространства компоненты вектора E – Ex, Ey,
Ez и компоненты вектора dl – dlx dly dlz .
E iEx jEy kEz
Где векторы i , j и k – соответствующие орты
dl idlx jdl y kdlz idx jdy kdz
Тогда
(3.17)
28.
Edl iEx jE y kEz idx jdy kdzi i 1, j j 1, k k 1,
i j 0
d Edl Ex dx E y dy Ez dz
d Ex dx E y dy Ez dz
Ex
,
x
Ey
,
y
Подставляя (3.19) в (3.17), получим
Ez
z
(3.18)
(3.19)
29.
E ij
k
y
z
x
E grad ( )
E
(3.20)
(3.21)
30. Эквипотенциальные поверхности.
Введем понятие эквипотенциальной поверхности — поверхности, во всех точкахкоторой потенциал имеет одно и то же значение. Убедимся в том, что вектор Е
направлен в каждой точке по нормали к эквипотенциальной поверхности в сторону
уменьшения потенциала . В самом деле, из формулы (3.20) следует, что проекция
вектора Е на любое направление, касательное к эквипотенциальной поверхности в
данной точке, равна нулю. А это значит, что вектор Е нормален к данной поверхности.
Далее, возьмем перемещение dl по нормали к поверхности в сторону уменьшения ,
тогда d < 0 и согласно (3.20) El>0, т. е. вектор Е направлен в сторону уменьшения ,
или в сторону, противоположную вектору . Эквипотенциальные поверхности
наиболее целесообразно проводить так, чтобы разность потенциалов для двух
соседних поверхностей была бы одинаковой. Тогда по густоте эквипотенциальных
поверхностей можно наглядно судить о значении напряженности поля в разных точках.
Там, где эти поверхности расположены гуще («круче потенциальный рельеф»), там
напряженность поля больше.
31.
Далее, ввиду того, что вектор Е всюду нормален кэквипотенциальной поверхности, линии вектора Е
ортогональны этим поверхностям.
На рис. показана двухмерная
картина
электрического
поля:
пунктиром
—
эквипотенциали, сплошными линиями — линии
вектора Е. Такое изображение придает большую
наглядность. Сразу же видно, в какую сторону
направлен вектор Е, где напряженность больше, где
меньше, где больше крутизна потенциального
рельефа. С помощью таких картин можно получить и
качественные ответы на ряд вопросов: куда начнет
двигаться заряд при помещении его в ту или иную
точку, где больше градиент потенциала (по модулю),
в какой точке поля на заряд будет действовать
большая сила и др.
32.
О преимуществах потенциала. Ранее было отмечено, что электростатическоеполе исчерпывающим образом характеризуется векторной функцией Е(r). Какая же
польза от введения потенциала Существует несколько весомых причин, убедительно
свидетельствующих о том, что потенциал — понятие действительно весьма
полезное, и не случайно, что этим понятием широко пользуются не только в физике,
но и в технике.
1. Зная потенциал (r), можно предельно просто вычислить работу сил поля при
перемещении точечного заряда q из точки 1 в точку 2:
A q 2 1
(3.22)
где 1 и 2 — потенциалы в точках 1 и 2. Значит, искомая работа равна убыли
потенциальной энергии заряда q в поле при перемещении его из точки 1 в точку 2.
Расчет работы сил поля по формуле (3.22) оказывается не только проще, но в
некоторых случаях и единственно возможным.
33. ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ
Электрический диполь — это системаиз двух одинаковых по модулю
разноименных точечных зарядов +q и
–q, находящихся на некотором
расстоянии l друг от друга. Когда
говорят
о
поле
диполя,
то
предполагают сам диполь точечным, т.
е. считают расстояния r от диполя до
интересующих
нас точек поля
значительно больше l.
34.
Поле диполя обладает осевойсимметрией, поэтому картина поля в
любой плоскости, проходящей через
ось диполя, одна и та же и вектор Е
лежит в этой плоскости.
Найдем сначала потенциал поля
диполя, а затем его напряженность.
Потенциал поля точечного заряда
определяется как
35.
q4 0 r
Тогда для диполя в точке Р (рис. ) определяется как
q 1 1
q r r
4 0 r r 4 0 r r
q
4 0 r
q
4 0 r
q(r r )
4 0
r r
1
Так как r > l, то, как видно из рис.а
r- - r+ = lcos и r+r- = r2, где r —
расстояние от точки Р до диполя (он точечный!). С учетом этого
36.
ql cos4 0 r 2
1
(3.23)
Обозначим
p ql
— электрический момент диполя. Этой величине сопоставляют вектор,
направленный по оси диполя от отрицательного заряда к
положительному:
p cos
4 0 r 2
1
(3.24)
Из формулы (3.23) видно, что поле диполя зависит от его электрического
момента р. Как мы увидим далее, и поведение диполя во внешнем поле также
зависит от р. Следовательно, р является важной характеристикой диполя.
37.
Следует также обратить внимание на то, что потенциал поля диполя убывает срасстоянием r быстрее, чем потенциал поля точечного заряда (1 /r2 вместо 1 /r).
Для нахождения поля диполя воспользуемся формулой
d Edl
Откуда следует
E d / dl
Введем систему ортогональную координат, связанную
с вектором r и вектором, перпендикулярным вектору r.
Обозначим орты этих направлений er и e . Найдем
проекции
вектора
Е
на
эти
два
взаимно
перпендикулярных направления (рис. б):
1 2 p cos
Er
r 4 0
r3
1 p sin
E
r 4 0 r 3
38.
Отсюда модуль вектора ЕE E E
2
r
2
p
4 0 r 3
4 cos 2 sin 2
1
p
2
E
1 3cos
3
4 0 r
В частности, при =0 и =π/2 мы получим
(3.25)
1
2p
E
4 0 r 3
1
p
E
4 0 r 3
соответственно, т. е. при одном и том же r напряженность E при =0 вдвое больше
E при = π/2 .
39. Сила, действующая на диполь.
Поместим диполь во внешнее неоднородное электрическое поле. Пусть Е+ и Е- –напряженности внешнего поля в точках, где расположены положительный и
отрицательный заряды диполя. Тогда результирующая сила F, действующая на диполь,
равна (рис. а):
F qE qE q E E
E E - это приращение Е вектора Е на отрезке, равном
длине диполя l , в направлении вектора l.
Вследствие малости этого отрезка можно записать
E
E
E E E
l
l
l
l
40.
После подстановки этого выражения в формулу для F получим, что сила,F q E E
E
ql
l
E
F p
l
(3.26)
где р = ql — электрический момент диполя. Входящую в это выражение производную
принято называть производной вектора по направлению. Знак частной производной
подчеркивает, что эта производная берется по определенному направлению —
направлению, совпадающему с вектором l или р.
41.
Простота формулы (3.26), к сожалению, обманчива: производная дЕ/дl являетсядовольно сложной математической операцией. Мы не будем останавливаться на этом
более подробно, а обратим внимание на существо полученного результата. Прежде
всего отметим, что в однородном поле
E
0
l
поэтому и F = 0. Значит, сила действует на диполь, вообще говоря, только в
неоднородном поле. Далее, направление вектора F в общем случае не совпадает ни с
вектором Е, ни с вектором р. Вектор F совпадает по направлению лишь с элементарным
приращением вектора Е, взятым в направлении вектора l или р (рис. б).
42.
На рис. показаны направления силы F, действующей на диполь в поле положительноготочечного заряда q, при трех разных расположениях диполя.
Если нас интересует проекция силы F на некоторое
направление x, то достаточно записать равенство (3.26) в
проекциях на это направление, и мы получим
Ex
Fx p
l
E x
l — производная соответствующей проекции вектора Е
опять же по направлению вектора l или р.
43.
Пусть диполь с моментом р расположен вдоль оси симметрии некоторогонеоднородного поля Е. Возьмем положительное направление оси x,
например, как показано на рис.
Так как в направлении вектора р приращение
проекции Ех будет отрицательным, то Fx<0, а
значит, вектор F направлен влево — в
сторону, где напряженность поля больше.
Если же вектор р на этом рисунке повернуть
на 90° так, чтобы центр диполя совпадал с
осью симметрии поля, то нетрудно
сообразить, что в таком положении Fх= 0.
44. Момент сил, действующих на диполь.
Рассмотрим, как ведет себя диполь во внешнем электрическом поле в своей системецентра масс — будет он поворачиваться или нет. Для этого мы должны найти момент
внешних сил относительно центра масс диполя. Относительно центра масс, чтобы
исключить момент сил инерции.
По определению момент сил F qE
F qE
относительно центра масс С равен
M r F r F r qE r qE
M (r r )qE
С учетом того, что
r r l
p ql
45.
M pE(3.28)
Этот момент сил стремится повернуть диполь так, чтобы его электрический момент р установился по направлению внешнего поля Е. Такое
положение диполя является устойчивым.
Итак, в неоднородном электрическом поле диполь будет вести себя
следующим образом: под действием момента сил (3.28) диполь будет
стремиться установиться по полю
p E
а под действием результирующей силы (3.26) —переместится в
направлении, где Е по модулю больше. Оба движения будут совершаться
одновременно.
46. Энергия диполя в поле.
W qМы знаем, что энергия точечного заряда q во внешнем поле равна
где – потенциал поля в точке нахождения заряда q. Диполь — это система из двух
зарядов, поэтому его энергия во внешнем поле
W q q q( )
где + и _ — потенциал внешнего поля в точках расположения зарядов + q и — q. С
точностью до величины второго порядка малости
l
l
где
d /dl
—
вектора l. Согласно
производная
потенциала
по
направлению
47.
El
El l El
W q( ) qlE pE
W pE
(3.29)
Из этой формулы следует, что минимальную энергию диполь имеет в положении
устойчивого равновесия.
p E
При отклонении из этого положения возникает момент внешних сил,
возвращающий диполь к положению равновесия.

























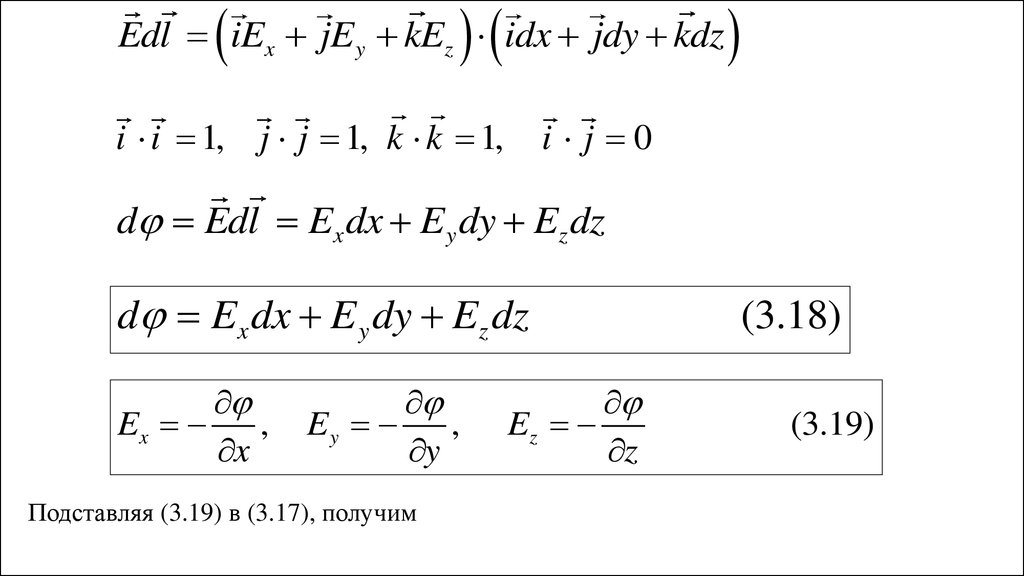



















 physics
physics








