Теорема Гаусса для диэлектриков

1.

Тема 1
Основы электростатики

2.

Лекция 3

3. Теорема Гаусса для диэлектриков

ФE
S
D dS q
n
s
k
qk
E dS
n
ε 0ε
divD

4.

Энергия поля
Есть три возможности посчитать энергию электростатического поля:
• С помощью интегрирования электростатического поля по пространству:
wуд
0 E
2
2
ED
wуд
2
• С помощью вычисления потенциалов и суммирования
по всем зарядам:
1 N
W qi φi
2 i 1
• Специальный случай, когда известна емкость системы или систему
можно считать конденсатором:
2
q
W
2C

5. Задача

Чему равна энергия электростатического поля заряженной сферы?
(Q – заряд, R- радиус)
ED
ED
W
dV
4 r 2 dr
2
2
R
1
Q
E
4 0 R
1 Q
D
4 R
ED
1
1
Q2
1 Q2
2
W
dV
4 r dr
2
4
2
2 R 4 0 r
8 0 R

6. Задача (второй метод)

Чему равна энергия электростатического поля заряженной сферы?
(Q – заряд, R- радиус)
1 N
U
W qi i
2 i 1
2
1 Q
U
4 0 R
QU
Q2
W
2
8 0 R
N
U
qi Q
2
i 1

7. Задача (третий метод)

Чему равна энергия электростатического поля заряженной сферы?
(Q – заряд, R- радиус)
Cшар. = 4 πεε0R
Q2
Wc
2C
Q2
Q2
Wc
2Cшар 8 0 R

8.

Притяжение пластин конденсатора
Силу их притяжения называют пондермоторной.
При незначительном перемещении одной пластины в
поле другой совершается работа:
dW
dA dW Fdx, F
dx
отсюда можно получить формулу для расчета
пондермоторной силы
2
F
q
2
2 0 S
.
2
Q
Q dx
dW d
.
2C 2 0 S

9. Диэлектрик втягивается в конденсатор

С какой силой втягивается диэлектрическая пластинка в пространство
между обкладками прямоугольного плоского конденсатора?
F
C
dW
dx
0S
d
Q2 1
F
( )
2 x C
[( 1)
x
1]
L
C
0 S ( x / L)
d
Q2d
1
F
2 0 SL [( 1) x 1]2
L
0 S (1 x / L)
d

10. Вопросы

Q2d
1
F
2 0 SL [( 1) x 1]2
L
• Изменится ли сила, если конденсатор будет
подключен к батарее?
• Как будет выглядеть закон сохранения энергии при
наличии батареи?
• Какие силы вызывают втягивание диэлектрика в
конденсатор? И как они направлены?

11.

Где работает диэлектрик ?
Почему в нем ослабевает поле?

12. Поляризация диэлектриков

• Все известные в природе вещества, в
соответствии с их способностью проводить
электрический ток, делятся на
три основных класса:
• диэлектрики
• полупроводники
• проводники
д 10 18 10 8 Ом 1 м 1
д п/п пр .
пр 10 10 Ом м
2
8
1
1

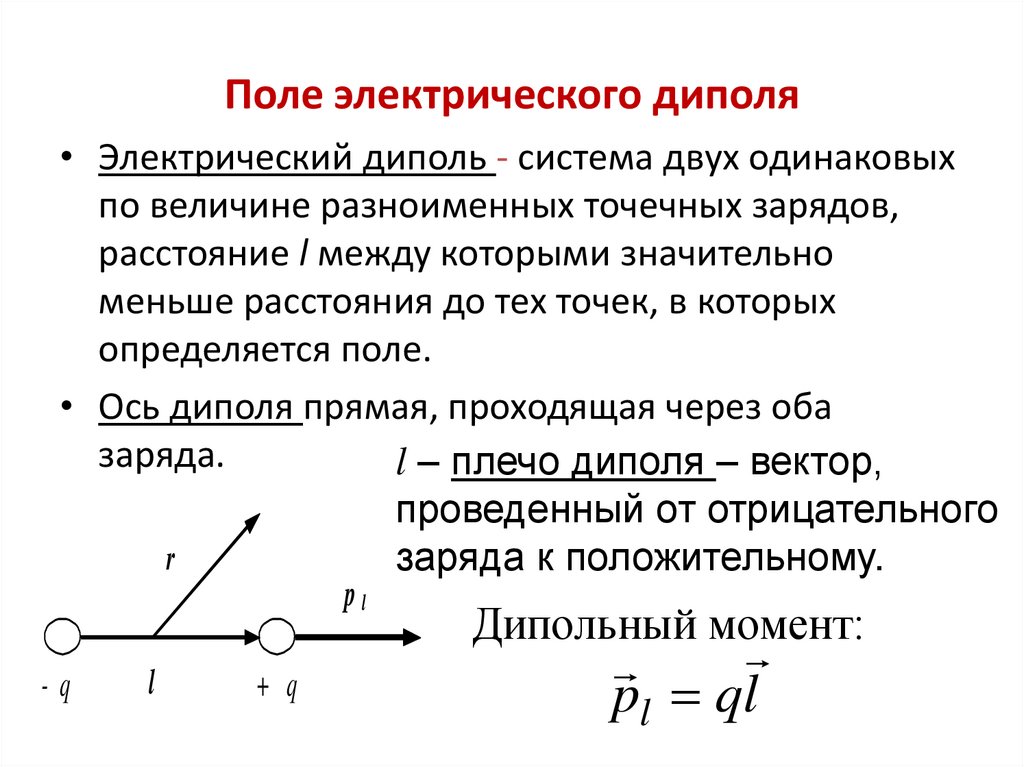
13. Поле электрического диполя

• Электрический диполь - система двух одинаковых
по величине разноименных точечных зарядов,
расстояние l между которыми значительно
меньше расстояния до тех точек, в которых
определяется поле.
• Ось диполя прямая, проходящая через оба
заряда.
l – плечо диполя – вектор,
проведенный от отрицательного
r
заряда к положительному.
pl
-q
l
+ q
Дипольный момент:
pl ql

14. Поле электрического диполя

r >> l → Диполь можно
рассматривать
как
систему 2-х точечных
зарядов.
Молекула воды Н2О обладает дипольным
моментом р = 6,3 10 30 Кл м.
Вектор дипольного момента направлен от
центра иона кислорода О2 к середине прямой,
соединяющей центры ионов водорода Н+.

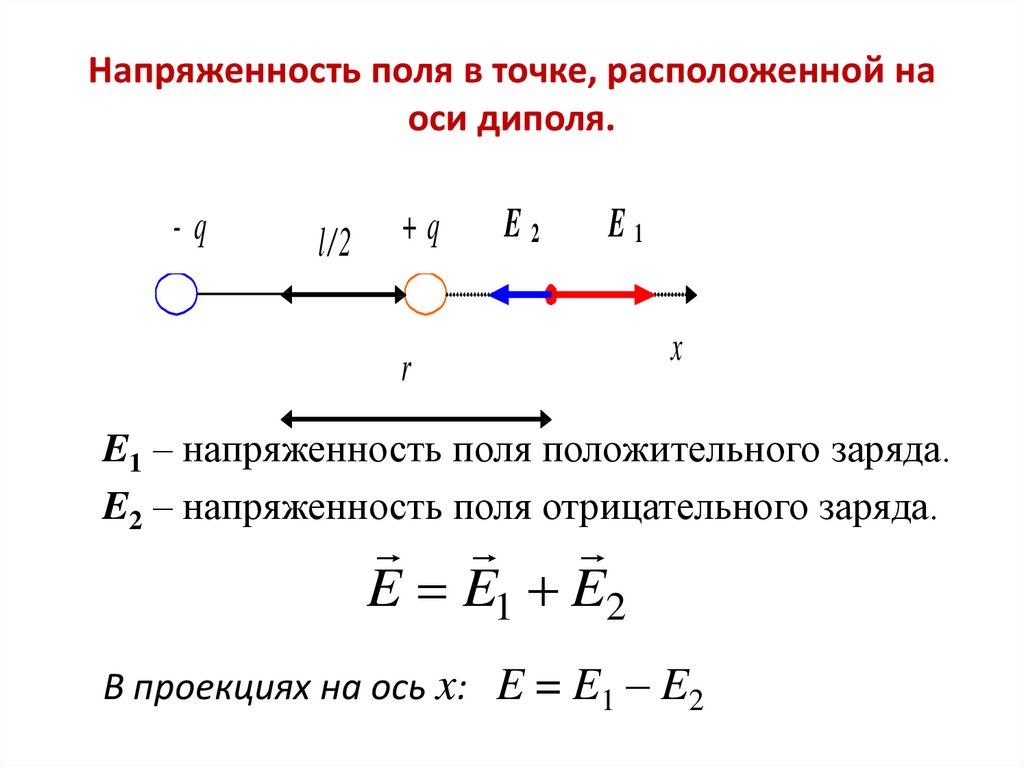
15. Напряженность поля в точке, расположенной на оси диполя.

-q
l/2
+q
E2
E1
r
x
E1 – напряженность поля положительного заряда.
E2 – напряженность поля отрицательного заряда.
E E1 E2
В проекциях на ось x: E = E1 – E2

16. Напряженность поля в точке, расположенной на оси диполя

-q
l/2
+q
r
E2
E1
x
l
l
(r ) 2 (r ) 2
1
q
1
q
q
2
2
E
4 0 (r l ) 2 4 0 (r l ) 2 4 0 (r l ) 2 (r l ) 2
2
2
2
2
l
r l ( r ) r ,
2
q 2rl
2ql
E
.
4
3
4 0 r
4 0 r
l
( r ) r .
2
E
pl
2 0 r 3

17. Напряженность поля диполя в точке, лежащей на перпендикуляре, восстановленном к его середине

E 2
1
q
4 0
2
l
2
(r )
4
l
2
l
2 r
4
l2
r l 0
4
2
E1
α
E
E
E2 r
α
-q
pl
α
l/2
+q
pl
4 0 r
3
ql
4 0 r 3
E pl
pl ql

18. Выводы

E
pl
0r
3
.
Поле диполя убывает быстрее в зависимости
от расстояния по сравнению с полем
точечного заряда.

19.

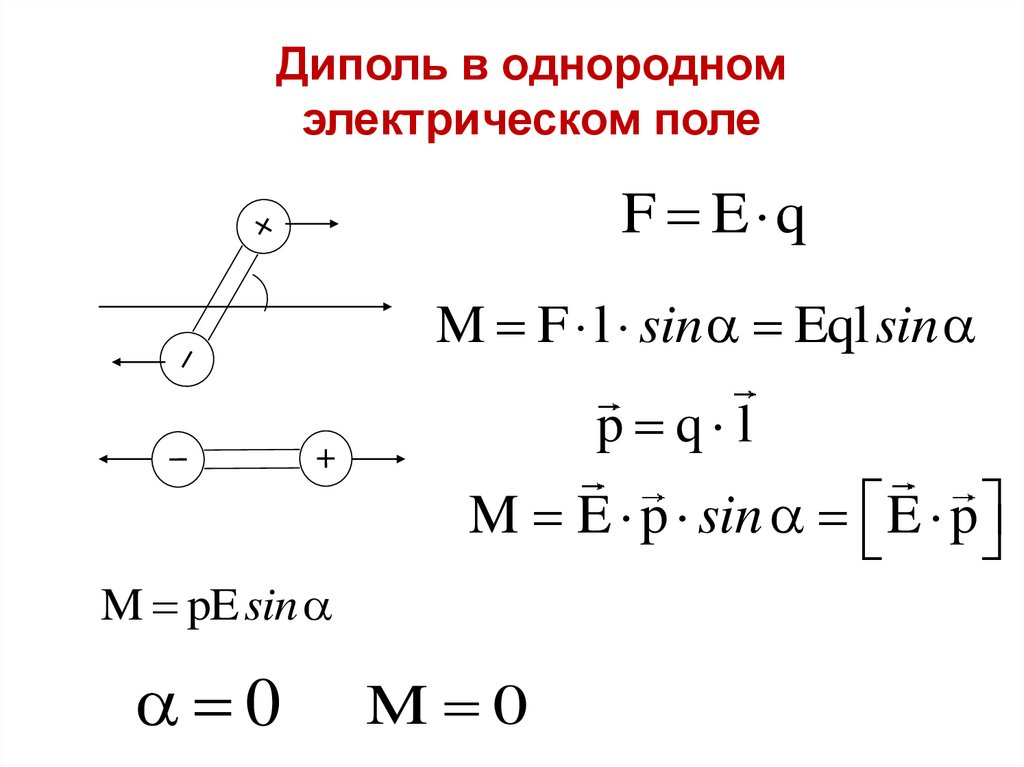
Диполь в однородном
электрическом поле
F E q
M F l sin Eql sin
p q l
M E p sin E p
M pE sin
0
M 0

20. Диполь в неоднородном электрическом поле

W q
d
W q l
dx
d
l
dx
W p E
dW
dE
Fx
p
dx
dx

21. Вопросы

• Как будет вести себя диполь в поле плоского
конденсатора?
• В поле цилиндрического конденсатора?
• В поле сферического конденсатора?

22.

• В идеальном диэлектрике свободных зарядов нет
способных перемещаться на значительные расстояния.
• Однако, это не значит, что идеальный диэлектрик,
помещенный в электростатическое поле, не реагирует
на него.
• Смещение электрических зарядов вещества под
действием электрического поля называется
поляризацией.
• Способность к поляризации является основным
свойством диэлектриков c точки зрения
электростатики.

23.

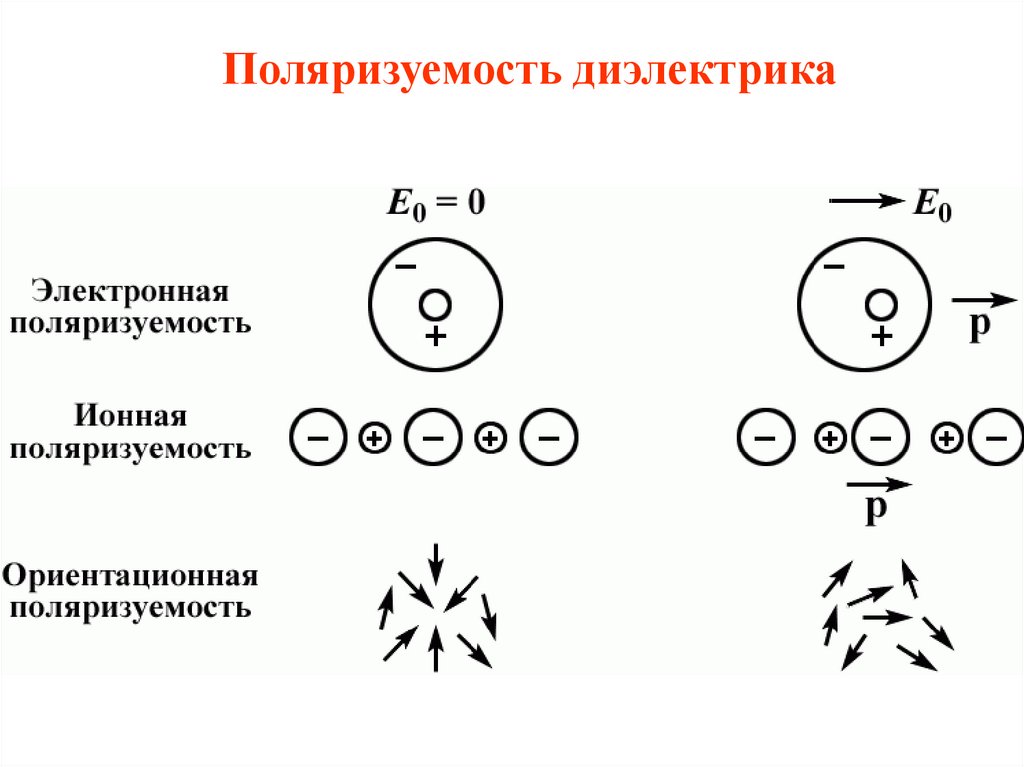
Поляризуемость диэлектрика

24.

• Внутри диэлектрика электрические заряды
диполей компенсируют друг друга.
• Но на внешних поверхностях диэлектрика,
прилегающих к электродам, появляются заряды
противоположного знака (поверхностно
связанные заряды).

25.

• Пусть E' – электростатическое поле связанных
зарядов. Оно направлено всегда против внешнего
поля E 0
• Следовательно, результирующее
электростатическое поле внутри диэлектрика
E E0 E '.

26.

Поместим диэлектрик в виде параллелепипеда
в
электростатическое поле
E0
Электрический момент тела, можно найти по
формуле:
P q l σ' S l , или P σ' Slcosφ,
σ'
– поверхностная плотность связанных зарядов

27.

• вектор поляризации –дипольный момент
единичного объема.
n
P P1k nP1 ,
k
• где n – концентрация молекул в единице
объема,
• P1 – дипольный момент одной молекулы.

28.

σ' P n
• Поверхностная плотность поляризационных
зарядов равна нормальной составляющей
вектора поляризации в данной точке
поверхности.
• Индуцированное в диэлектрике
электростатическое поле E' будет влиять только
на нормальную составляющую вектора
напряженности электростатического поля E .

29.

• Вектор поляризации можно представить так:
•
P nP1 nαε0E χε 0E,
• где
α – поляризуемость молекул,
• χ nα – диэлектрическая восприимчивость –
макроскопическая безразмерная величина,
характеризующая поляризацию единицы
объема.

30.

• Величина ε 1 χ характеризует
электрические свойства диэлектрика.
• Физический смысл диэлектрической
проницаемости среды:
ε – величина, показывающая во сколько
раз электростатическое поле внутри
диэлектрика меньше, чем в вакууме:
E0
ε
.
E

31. Вопросы

• Как будет вести себя диэлектрический шарик
в поле плоского конденсатора?
• В поле цилиндрического конденсатора?
• В поле сферического конденсатора?