Similar presentations:
Электростатическое поле в диэлектрике. Лекция 3
1. Лекция № 3
ЭЛЕКТРОСТАТИЧЕСКОЕПОЛЕ В ДИЭЛЕКТРИКЕ
2. Электрический диполь в э/ст поле
Электрический диполь – система двухразноименных точечных зарядов +q и q.
r l
_
q
p
l
+
+q
ось
диполя
l
Электрический дипольный момент
p ql
(3.1)
3.
Nr
q
l
q
r
Потенциал поля диполя
q q
1
4 0 r r
k0 q r r
r r
Так как r>>l (диполь точечный), то
2
r r l cos и r r r
k0 p cos k0
3 rp
2
r
r
(3.2)
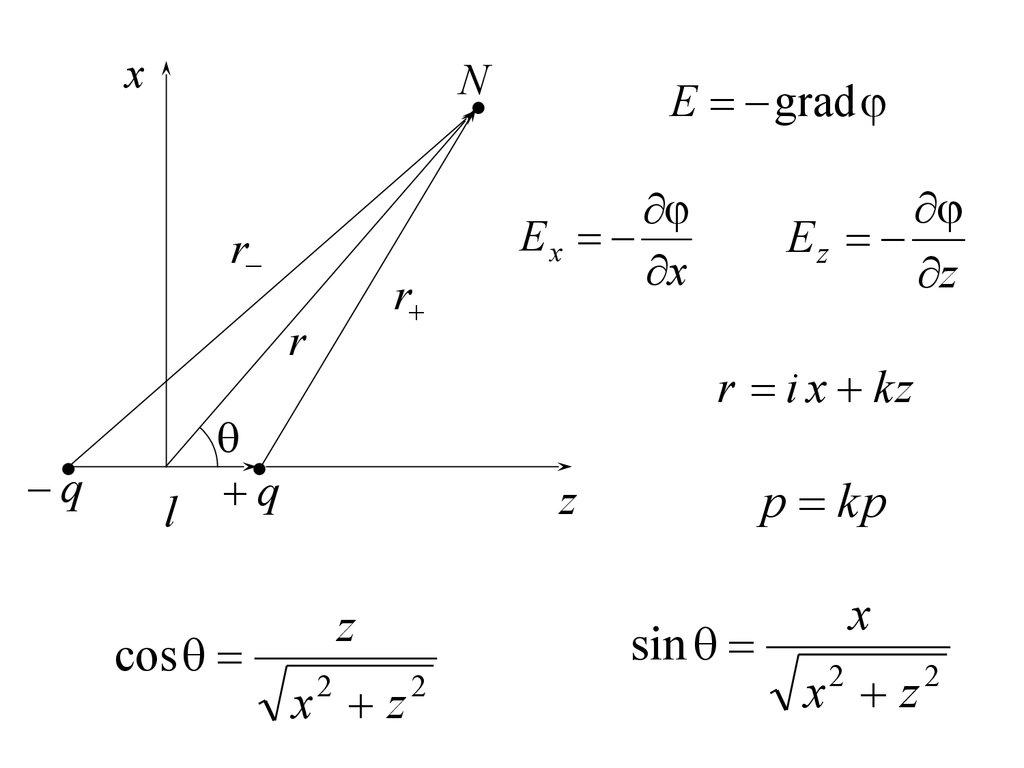
4.
xr
r
r
q
E grad
N
q
l
cos
Ez
z
Ex
x
r i x kz
p kp
z
z
2
x z
2
sin
x
2
x z
2
5.
k0 pz
1
2
k
pz
x
2
0
2
x2 z 2 x z
3 2
2
k0 pz x z
Ex
x
2
2
3k 0 pxz x
5
2 2
z
3
z2 2
5
2 2x
1
3k 0 p cos sin 3
r
6.
22
E z k0 p x z
z
3
2
3 2
z x
2
5
2 2
z
2z
cos 2 1
k
p
2
0
k0 p 3 3 3 3 3 cos 1
r
r
r
E
1 4 0
2
Ex
2
Ez
k0 p
2
2
4
2
9 cos sin
9 cos 6 cos 1
3
r
1 cos 2
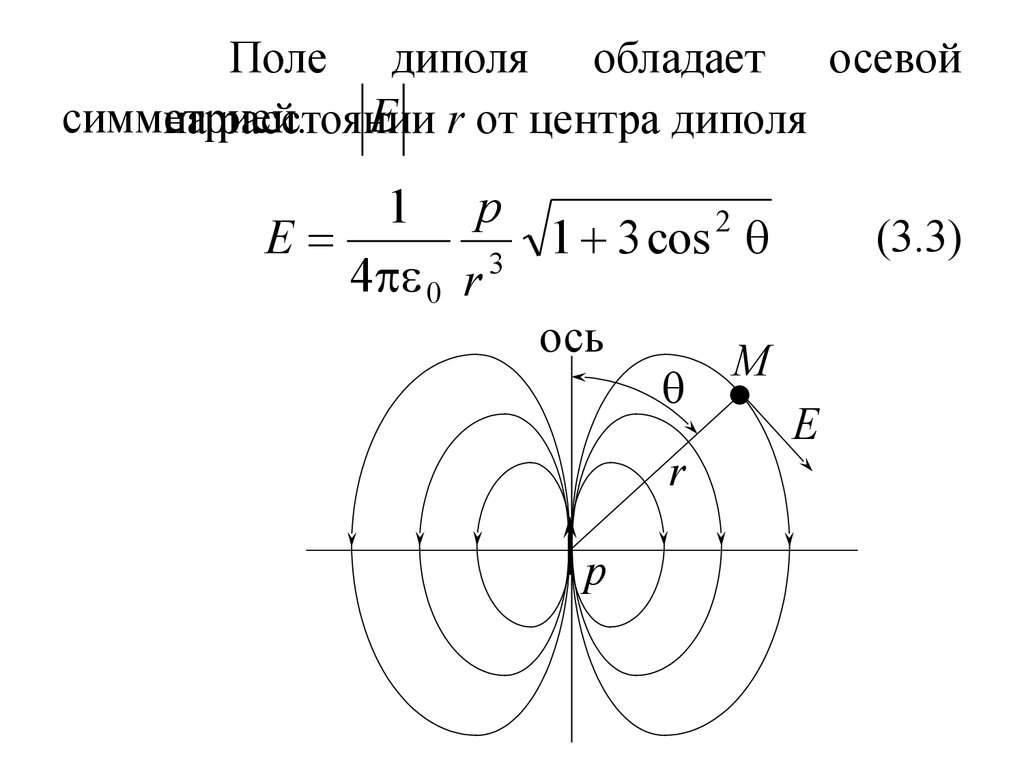
7. Поле диполя обладает осевой симметрией.
Поле диполя обладает осевойE r от центра диполя
симметрией.
на расстоянии
1 p
2
E
1
3
cos
4 0 r 3
ось
r
p
М
(3.3)
E
8. Диполь в однородном электрическом поле
E constM
F qE
q
F qE
q
p
h l sin
F F F
E
9.
M Fl sin qEl sin pE sinС учетом направлений p, E , M
M p, E
(3.4)
M = 0, если = 0 или = π (положения
устойчивого и неустойчивого равновесия
соответственно).
Под действием момента сил M
диполь будет стремиться установиться по
полю p E
10. Диполь в неоднородном электрическом поле
MF
q
q
p
F
E
x l cos
С учетом малых размеров диполя
F qE
E E x , y , z
x
F qE
E E x x, y, z
11.
Проекциярезультирующей
силы,
действующей на диполь в направлении оси x
E
x
Fx F F q E E q E q
x
E
E
Fx q l cos p cos
x
x
При
0< <π/2
направление
результирующей силы, действующей на
диполь со стороны электрического поля,
таково, что диполь втягивается в область
более сильного поля. При π> >π/2 диполь
выталкивается из поля.
12. Потенциальная энергия диполя, помещенного в однородное электрическое поле
dWp d A M dWp
2
2
M
d
pE sin d
pE cos 2 pE cos pE
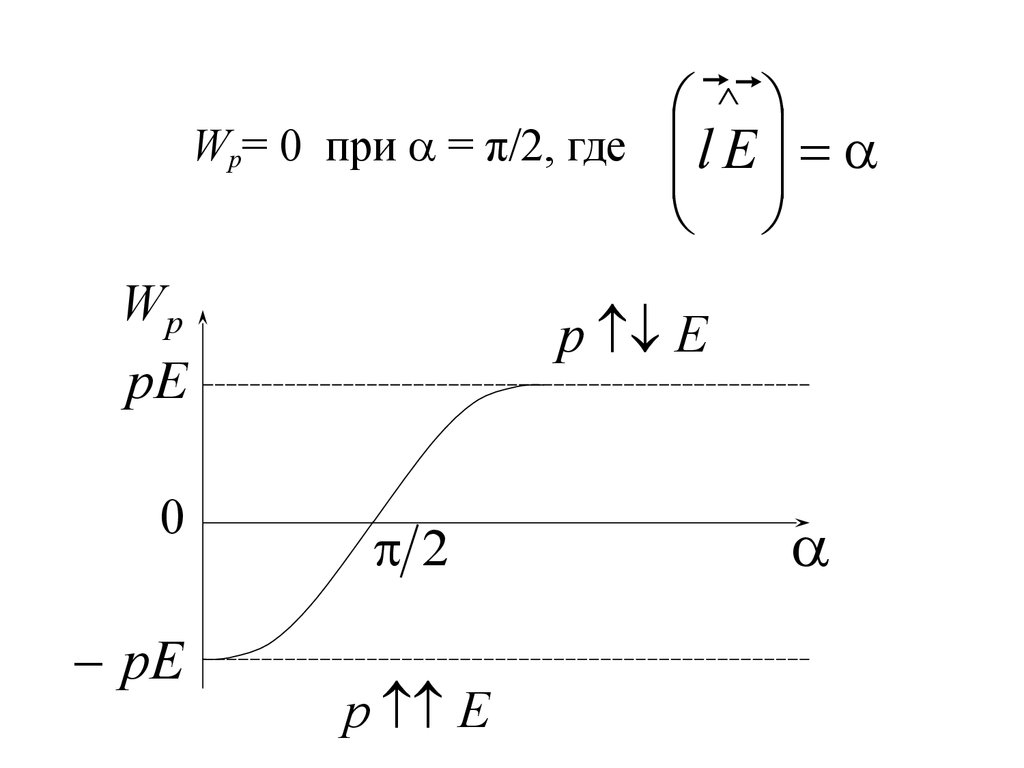
13.
Wp= 0 при = π/2, гдеp E
Wp
pE
0
pE
l E
2
p E
14.
15.
Выделим малый объем диэлектрика ввиде наклонной призмы. Ее дипольный
момент
(3.8)
p q l S l
S E
Т.к. поляризованность
n определяет
дипольный
момент
единицы
объема
диэлектрика, то дипольный
момент призмы
p P V P S l cos (3.9)
l
Приравниваем (3.8) и (3.9)
P cos Pn
(3.10)
16.
При неоднородной поляризации диэлектрикасвязанные заряды появляются не только на
поверхности диэлектрика, но и в его объеме с
некоторой ρ .
Отрицательные
связанные
являются источником линий
P:
div P
заряды
(3.11)
Связанный поляризационный заряд
q d V
V
Тогда теорема Гаусса в интегральной
форме
q P d S
(3.12)
S
17. Вектор электрического смещения
D 0 E PВ СИ D [Кл/м2 ]
(3.13)
В изотропных диэлектриках
Тогда
P 0 E
(3.14)
D 1 0 E 0 E ,
(3.15)
1
В случае анизотропных диэлектриков D и E
могут быть неколлинеарными.
18. Обобщение теоремы Гаусса
1E d S q q
S
0
(3.16)
где q и q – сторонние и связанные заряды,
охватываемые поверхностью S
q P d S
Тогда
0 E P d S q
S
S
Теорема Гаусса для вектора электрического
смещения в интегральной
форме
(3.17)
DdS q
S
19. Поток
через замкнутуюповерхность равен
Поток
D
алгебраической сумме сторонних зарядов,
заключенных внутри этой поверхности.
В дифференциальной форме
div D
или
D
(3.18)
В диэлектриках обычно связанные заряды не
заданы и определить их можно только после
нахождения напряженности электрического
поля в диэлектрике, поэтому удобно
использовать (3.17) или (3.18), а не (3.16)
20. Поле на границе раздела диэлектриков
Выделим малый участок границыраздела 2-х диэлектриков с диэлектрическими
проницаемостями ε1 и ε2, на которой нет
распределенных сторонних зарядов. Границу
раздела будем считать плоской.
D1 и D2
– электрические смещения полей в
2-х диэлектриках вблизи границы раздела.
21.
n2n
2
1
D2
S h
n1
D1
Пусть h→0 а S достаточно мало. Из
теоремы Гаусса:
(3.19)
D2 n S D1n S 0
2
1
Учитывая, что n n2 n1 ,
D2 n D1n
(3.20)
22. Рассматривая диэлектрик с
D 0 E , из (3.20)2 E 2 n 1 E1n
(3.21)
Выделим прямоугольный замкнутый
контур; l достаточно мало, а h→0.
2
1
l
2
1
Из теоремы о циркуляции:
E1 l E 2 l 0
23.
илиE 2 E1
тогда
D 2 D1
2
1
D2
2
1
D1n
2
D1
1
D1
D2
(3.22)
(3.23)
D2 n
При переходе
через границу раздела 2-х
диэлектриков
линии
электрического
смещения
преломляются.
24. Из рисунка
D1tg 1
D1n
и
D2
tg 2
D2 n
С учетом (3.20) и (3.23):
D1n D 2 n
и 1 D 2 2 D1
получим
tg 1 D1 1
tg 2 D 2 2
(3.24)



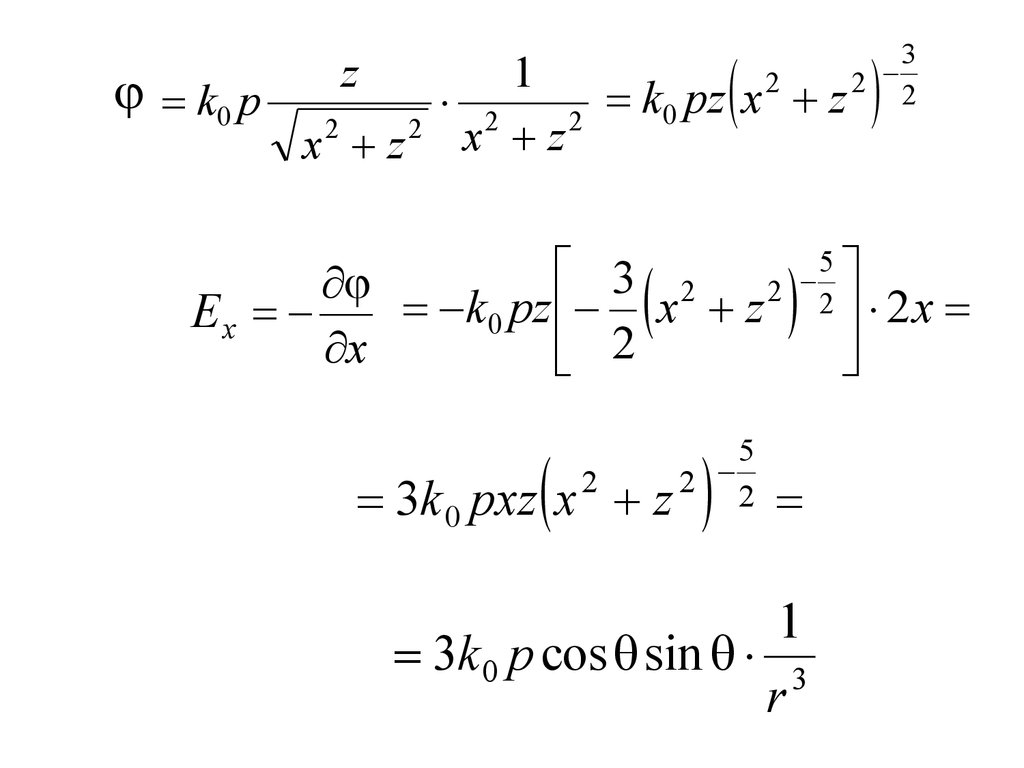

















 physics
physics








