Similar presentations:
Физика – наука о природе. Современная физика – наука, изучающая общие свойства материи – вещества и поля
1.
2.
ФИЗИКА – НАУКА О ПРИРОДЕ.СОВРЕМЕННАЯ ФИЗИКА – НАУКА,
ИЗУЧАЮЩАЯ ОБЩИЕ СВОЙСТВА
МАТЕРИИ – ВЕЩЕСТВА И ПОЛЯ.
Первый шаг при выбранной концепции
построения курса физики – Механика
рассматривала физические модели:
материальная точка и абсолютно твердое
тело, не вникая во внутреннюю структуру.
Следующий шаг в познании свойств материи –
Статистическая физика устанавливает из
каких частей (атомов и молекул) состоит
тело, и как эти части взаимодействуют между
собой.
3.
Посколькуатомы
построены
из
электрически заряженных частиц
(электронов и ядер), то следующий
шаг в познании строения вещества –
исследование
электромагнитных
взаимодействий.
Электричество
• Электростатика
• Постоянный ток
• Электромагнетизм
4.
Исторический очерк. Электрические явления былиизвестны в глубокой древности.
1) Порядка 500 лет до нашей эры Фалес Милетский
обнаружил, что потертый шерстью янтарь притягивает
легкие пушинки. Его дочь пыталась почистить шерстью
янтарное веретено и обнаружила этот эффект.
От слова «электрон», означающий по-гречески «янтарь» и
произошел термин «электричество». Термин ввел
английский врач Гильберт в XVI веке. Он обнаружил, что
еще ряд веществ электризуется.
2) При раскопках древнего Вавилона (4000 лет назад)
обнаружены сосуды из глины, содержащие железный и
медный стержни. На дне битум – изолирующий
материал. Стержни разъедены лимонной или уксусной
кислотой, то есть находка напоминает гальванический
элемент.
3) Золотое покрытие вавилонских украшений можно
объяснить только гальваническим способом их
нанесения.
5. Электростатика – раздел физики, изучающий взаимодействие и свойства систем электрических зарядов неподвижных относительно
выбраннойинерциальной системы отсчета.
• Электрический заряд – мера электрических
свойств тел или их составных частей.
Термин ввел Б.Франклин в 1749 г. Он же –
«батарея», «конденсатор», «проводник»,
«заряд», «разряд», «обмотка».
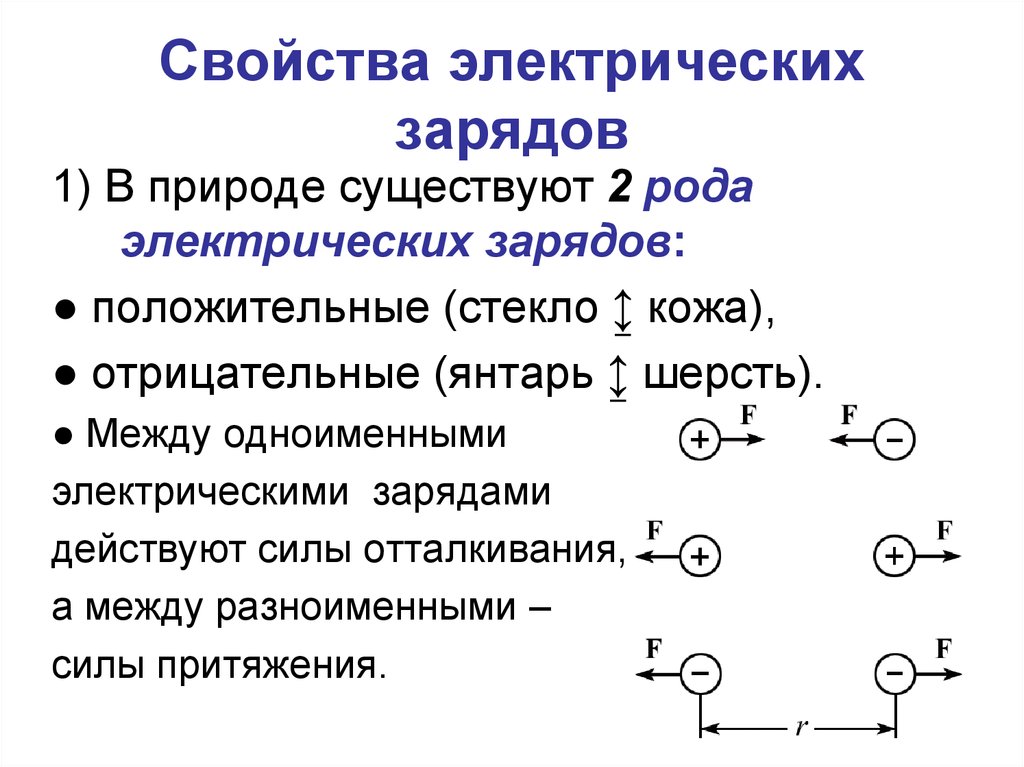
6. Свойства электрических зарядов
1) В природе существуют 2 родаэлектрических зарядов:
● положительные (стекло ↨ кожа),
● отрицательные (янтарь ↨ шерсть).
● Между одноименными
электрическими зарядами
действуют силы отталкивания,
а между разноименными –
силы притяжения.
7.
• Выбор наименований зарядовисторически случаен. Безусловный
смысл имеет только различие знаков
заряда. Законы не изменились бы, если
бы положительные заряды
переименовали в отрицательные и
наоборот: законы взаимодействия
зарядов симметричны к замене
+ q на – q.
8.
Фундаментальное свойство – наличиезарядов в двух видах – то, что заряды
одного знака отталкиваются, а
противоположного – притягиваются.
Причина этого современной теорией не
объяснена. Существует мнение, что
положительные и отрицательные
заряды – это противоположное
проявление одного качества.
9. Свойства электрических зарядов
2) Закон сохранения заряда –фундаментальный закон (экспериментально
подтвержден Фарадеем в 1845 г.)
Полный электрический заряд изолированной
системы есть величина постоянная.
Полный электрический заряд – сумма
положительных и отрицательных зарядов,
составляющих систему.
Под изолированной в электрическом поле
системой понимают систему, через границы
которой не может пройти никакое вещество,
кроме света.
10.
В соответствии с законом сохранения зарядаразноименные заряды рождаются и исчезают
попарно: сколько родилось (исчезло)
положительных зарядов, столько родилось
(исчезло) отрицательных зарядов. Два
элементарных заряда противоположных
знаков в соответствии с законом сохранения
заряда всегда рождаются и исчезают
одновременно.
Пример: электрон и позитрон, встречаясь друг
с другом, аннигилируют, рождая два или
более гамма-фотонов.
e – + e + 2g.
11.
Свет может входить и выходить из системы, ненарушая закона сохранения заряда, так как
фотон не имеет заряда; при фотоэффекте
возникают равные по величине
положительные и отрицательные заряды, а
фотон исчезает.
И наоборот, гамма-фотон, попадая в поле
атомного ядра, превращается в пару частиц –
электрон и позитрон.
g e – + e +.
12. Свойства электрических зарядов
3) Электрический заряд – инвариант,его величина не зависит от выбора системы
отсчета.
4) Электрический заряд – величина
релятивистки инвариантная,
не зависит от того движется заряд или покоится.
5) Квантование заряда, электрический заряд
дискретен, его величина изменяется скачком.
Опыт Милликена (1910 – 1914 гг.)
q = n e, где n целое число. Заряд любого
тела составляет целое кратное от
элементарного электрического заряда
е = 1,6 10 19 Кл (Кулон).
13.
Суммарный заряд элементарных частиц, есличастица им обладает, равен элементарному
заряду.
● Наименьшая частица, обладающая
отрицательным элементарным электрическим
зарядом, – электрон, me= 9,11·10-31 кг,
● Наименьшая частица, обладающая
положительным элементарным электрическим
зарядом, – позитрон, mр= 1,67·10-27 кг. Таким
же зарядом обладает протон, входящий в
состав ядра.
Равенство зарядов электрона и протона
справедливо с точностью до одной части на
1020. То есть фантастическая степень точности.
Причина неясна.
14.
Более точно: установлено, чтоэлементарные частицы представляют
собой комбинацию частиц с дробным
зарядом – кварков, имеющих заряды
1
2
e и e.
3
3
В свободном состоянии кварки не
обнаружены.
15. Свойства электрических зарядов
6) Различные тела в классической физике взависимости от концентрации свободных
зарядов делятся на
● проводники (электрические заряды могут
перемещаться по всему их объему),
● диэлектрики (практически отсутствуют свободные
электрические заряды, содержит только связанные
заряды, входящие в состав атомов и молекул),
● полупроводники (по электропроводящим
свойствам занимают промежуточное положение
между проводниками и диэлектриками).
16. Свойства электрических зарядов
Проводники делятся на две группы:1) проводники первого рода (металлы), в
которых перенос зарядов (свободных электронов)
не сопровождается химическими превращениями,
2) проводники второго рода (растворы
солей, кислот), перенос зарядов (+ и − ионов)
в них сопровождается химическими изменениями.
17. Свойства электрических зарядов
7) Единица электрического заряда вСИ [1 Кл] – электрический заряд,
проходящий через поперечное
сечение проводника при силе тока 1 А
за время 1 с.
q = I·t.
18. Закон Кулона – основной закон электростатики
Описывает взаимодействие точечных зарядов.• Точечный заряд сосредоточен на теле,
линейные размеры которого пренебрежимо
малы по сравнению с расстоянием до других
заряженных тел.
Точечный заряд, как физическая модель, играет в
электростатике ту же роль, что и материальная точка
и абсолютно твердое тело в механике, идеальный газ
в молекулярной физике, равновесные процессы и
состояния в термодинамике.
Закон впервые был открыт в 1772 г. Кавендишем.
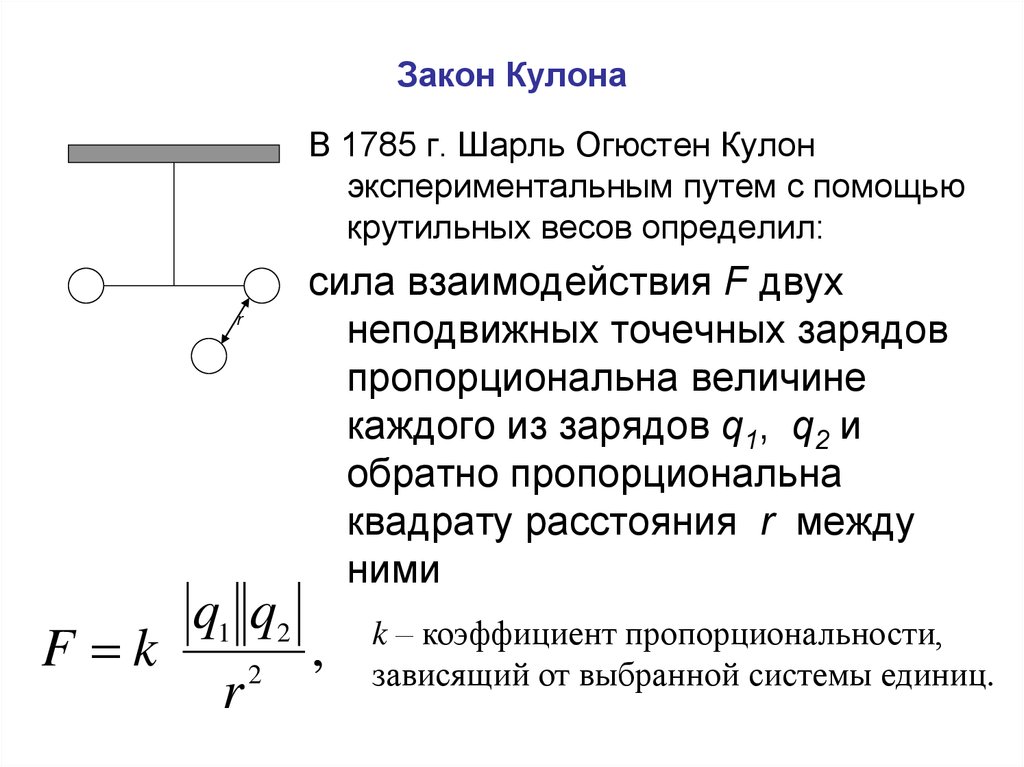
19. Закон Кулона
В 1785 г. Шарль Огюстен Кулонэкспериментальным путем с помощью
крутильных весов определил:
r
сила взаимодействия F двух
неподвижных точечных зарядов
пропорциональна величине
каждого из зарядов q1, q2 и
обратно пропорциональна
квадрату расстояния r между
ними
q1 q2
F k
,
2
r
k – коэффициент пропорциональности,
зависящий от выбранной системы единиц.
20. Закон Кулона
В опытах определялся вращающиймомент:
M g Fr.
r
Сам Кавендиш, работы которого
остались неизвестными, еще в
1770 г. получил «закон Кулона» с
большей точностью.
21. Закон Кулона
FСила
направлена по прямой, соединяющей
взаимодействующие заряды.
Кулоновская сила является центральной
силой.
22. Закон Кулона в векторном виде
F21 kСила – величина векторная.
Поэтому запишем закон
Кулона в векторном
виде.
1) Для произвольно
выбранного начала
отсчета.
q1 q2
3 (r2 r1 ),
( r2 r1 )
r2 r1
1
r2 r1
F12 F21
23. Закон Кулона в векторном виде
2) Начало отсчетасовпадает с одним
из зарядов.
q1 q2
F21 k
r
3
r
24. Закон Кулона
• Закон Кулона выполняется прирасстояниях
10-15 м < r < 4·104 км.
• В системе СИ: k =
1
4 0
H м2
2
Кл
= 9·109
[ м / Ф].
• В системе СГС: k = 1.
Кл 2
2
ε0 = 8,85·10-12
,[Ф / м] –
H м
электрическая постоянная.
25. Электрическое поле. Напряженность электрического поля
• Поле – форма материи, обуславливающаявзаимодействие частиц вещества.
• Электрическое поле – особая форма
существования материи, посредством
которого взаимодействуют электрические
заряды.
• Электростатическое поле - поле,
посредством которого осуществляется
кулоновское взаимодействие неподвижных
электрических зарядов.
Является частным случаем электромагнитного
поля.
26. Пробный точечный положительный заряд q0
используют для обнаружения и исследованияэлектростатического поля.
q0 не вызывает заметного перераспределения
зарядов на телах, создающих поле.
Силовая характеристика электростатического
поля определяет, с какой силой поле
действует на единичный положительный
точечный заряд q0. Такой характеристикой
является напряженность
электростатического поля.
27. Напряженность электрического поля – физическая величина, определяемая силой, действующей на пробный точечный положительный
заряд q0, помещенный вэту точку поля.
F
E
,
q0
q – источник
поля.
q0+ – пробный
заряд.
E Ex i E y j Ez k
E
2
Ex
2
Ey
2
Ez
28.
FE
.
q0
Напряженность электростатического поля в
данной точке численно равна силе,
действующей на единичный положительный
точечный заряд, помещенный в данную точку
поля.
29.
Зная напряженность поля в какой-либо точкепространства, можно найти силу,
действующую на заряд , помещенный в эту
точку:
F qE.
Это другой вид закона Кулона, который и вводит
понятие электрического поля, создающееся
зарядами во всем окружающем пространстве,
а также представляет закон действия данного
поля на любой заряд.
30. Напряженность поля точечного заряда в вакууме.
1 qq0F
1 q
F
r
E
r
3
3
4 0 r
q0 4 0 r
q – источник поля,
q0+ – пробный заряд.
31. Напряженность электрического поля
• E совпадает с направлением силы F, действующейна пробный заряд q0+ .
• Поле создается положительным зарядом – вектор
напряженности электрического поля E направлен
от заряда.
• Поле создается отрицательным зарядом – вектор
напряженности электрического поля E направлен
к заряду.
32. Напряженность электрического поля
• СИ: E измеряется в [1 Н /Кл = 1 В/м] –это напряженность такого поля, которое
на точечный заряд 1 Кл действует с
силой 1 Н.
33. Принцип суперпозиции напряженности электрического поля
Опытно установлено, что взаимодействие двухзарядов не зависит от присутствия других
зарядов.
В соответствии с принципом независимости
действия сил: на пробный заряд,
помещенный в некоторую точку, будет
действовать сила F со стороны всех зарядов
qi, равная векторной сумме сил Fi,
действующих на него со стороны каждого из
зарядов.
n
F F1 F2 ... Fn Fi
i 1
34. Принцип суперпозиции напряженности электрического поля
F q0 EFi q0 Ei
n
q0 E q0 Ei ,
i 1
n
E Ei
i 1
Напряженность электростатического поля,
создаваемого системой точечных зарядов
в данной точке, равна геометрической сумме
напряженностей полей, создаваемых в этой
точке каждым из зарядов в отдельности.
35. Первый способ определения напряженности электрического поля Е – с помощью закона Кулона и принципа суперпозиции.
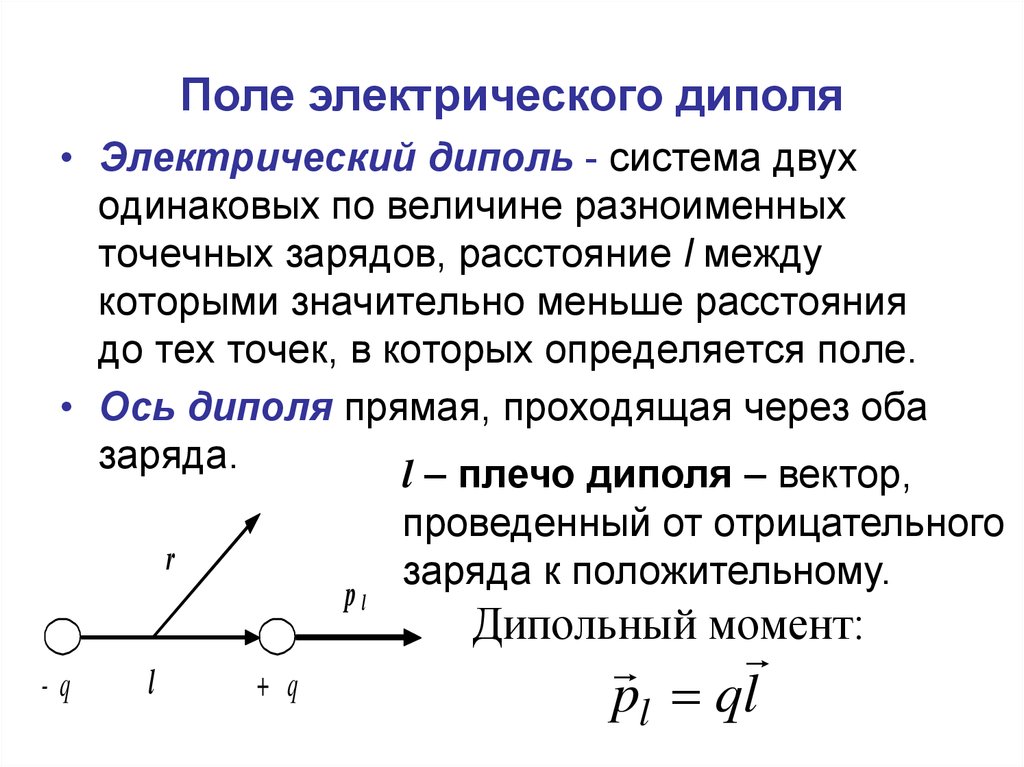
Поле электрического диполя36. Поле электрического диполя
• Электрический диполь - система двуходинаковых по величине разноименных
точечных зарядов, расстояние l между
которыми значительно меньше расстояния
до тех точек, в которых определяется поле.
• Ось диполя прямая, проходящая через оба
заряда.
l – плечо диполя – вектор,
r
pl
-q
l
+ q
проведенный от отрицательного
заряда к положительному.
Дипольный момент:
pl ql
37. Поле электрического диполя
r >> l → Дипольможно
рассматривать как систему
2-х точечных зарядов.
Молекула воды Н2О обладает дипольным
моментом р = 6,3 10 30 Кл м.
Вектор дипольного момента направлен от
центра иона кислорода О2 к середине прямой,
соединяющей центры ионов водорода Н+.
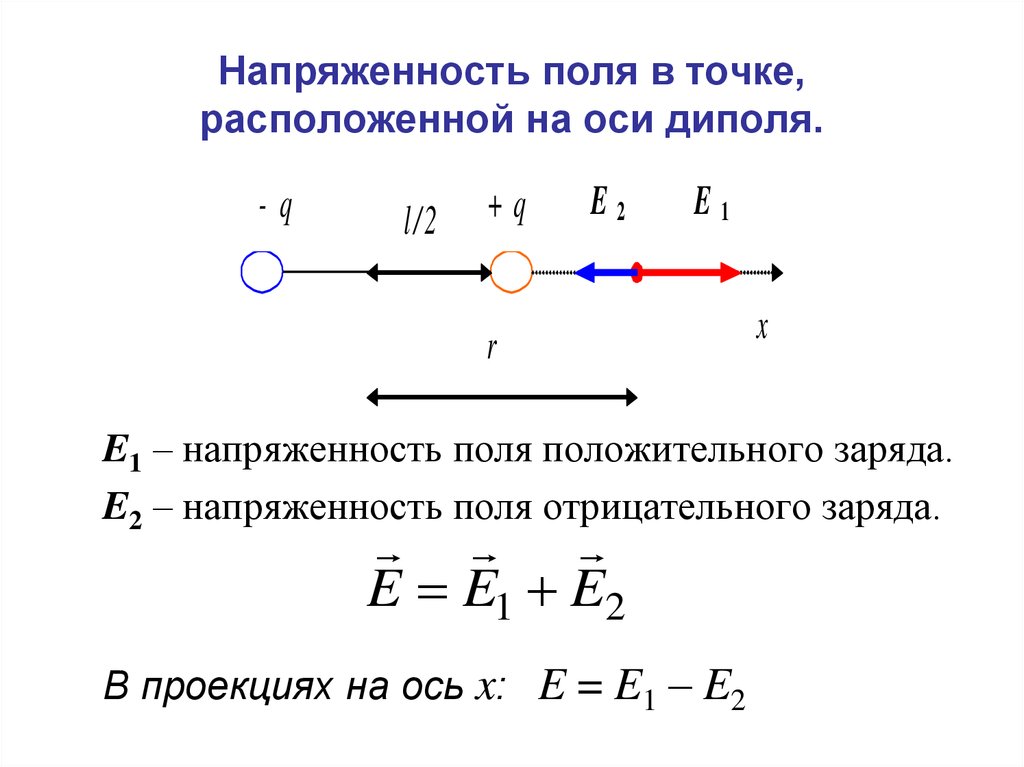
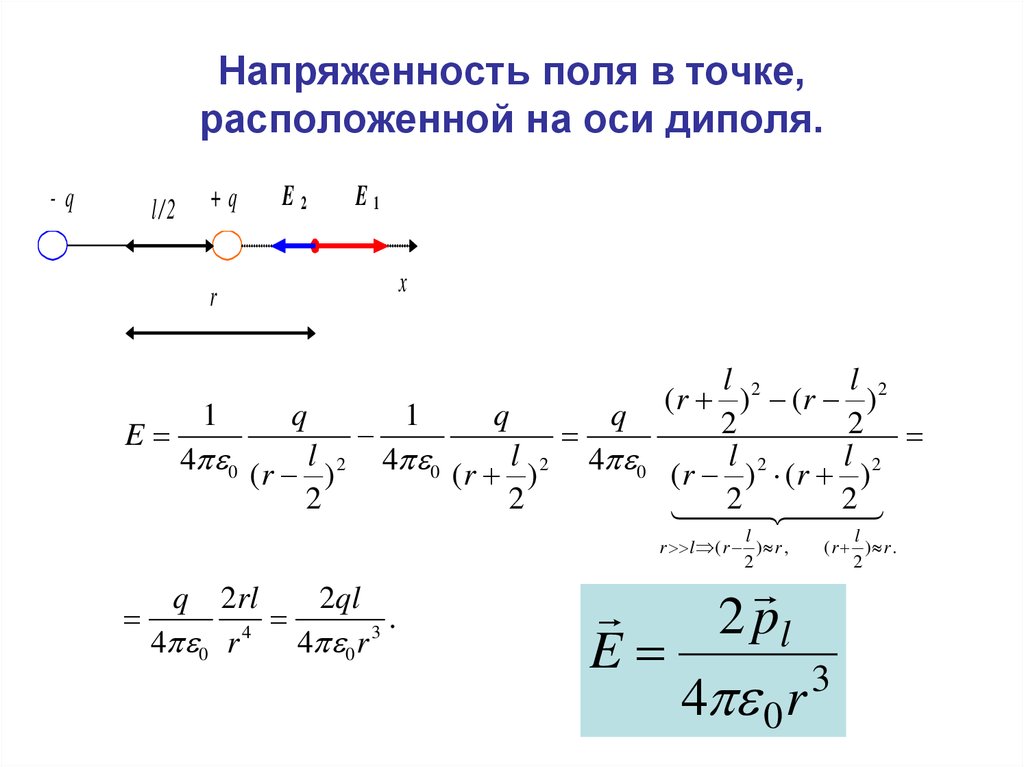
38. Напряженность поля в точке, расположенной на оси диполя.
-ql/2
+q
E2
E1
r
x
E1 – напряженность поля положительного заряда.
E2 – напряженность поля отрицательного заряда.
E E1 E2
В проекциях на ось x: E = E1 – E2
39. Напряженность поля в точке, расположенной на оси диполя.
-ql/2
+q
E2
E1
r
x
l
l
(r ) 2 (r ) 2
1
q
1
q
q
2
2
E
4 0 (r l ) 2 4 0 (r l ) 2 4 0 (r l ) 2 (r l ) 2
2
2
2 2
l
r l ( r ) r ,
2
q
2rl
2ql
.
4
3
4 0 r
4 0 r
E
2 pl
4 0 r
l
( r ) r .
2
3
40. Напряженность поля в точке, расположенной на оси диполя.
2 plE
.
3
4 0 r
Поле диполя убывает быстрее в
зависимости от расстояния по
сравнению с полем точечного заряда.
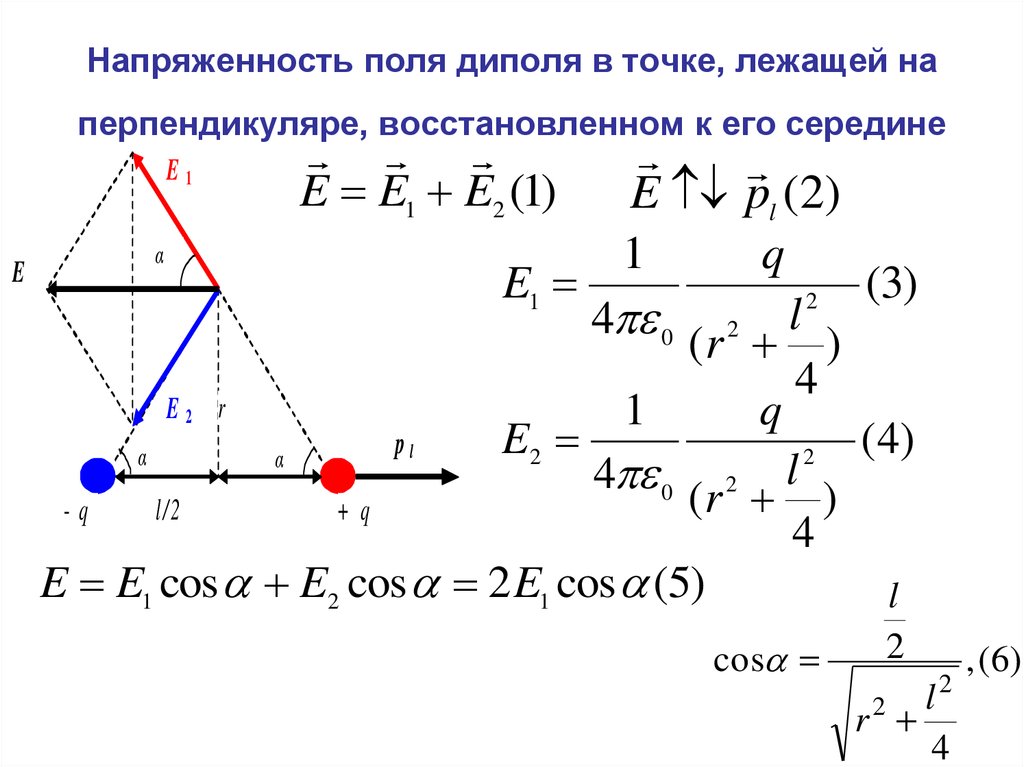
41. Напряженность поля диполя в точке, лежащей на перпендикуляре, восстановленном к его середине
E pl (2)1
q
E1
(3)
2
4 0 2 l
(r )
4
E E1 E2 (1)
E1
α
E
E2 r
α
α
pl
E2
1
4 0
q
2
l
(r )
-q
l/2
+q
4
E E1 cos E2 cos 2 E1 cos (5)
( 4)
2
cos
l
2
2
l
r2
4
, ( 6)
42. Напряженность поля диполя в точке, лежащей на перпендикуляре, восстановленном к его середине
Уравнения (3),(4), (6)→(5):E 2
1
q
4 0
2
l
2
(r )
4
l
2
l
2 r
4
l2
r l 0
4
2
ql
4 0 r 3
E pl
pl ql
E1
α
E
E2 r
α
-q
pl
α
l/2
+q
E
pl
4 0 r
3
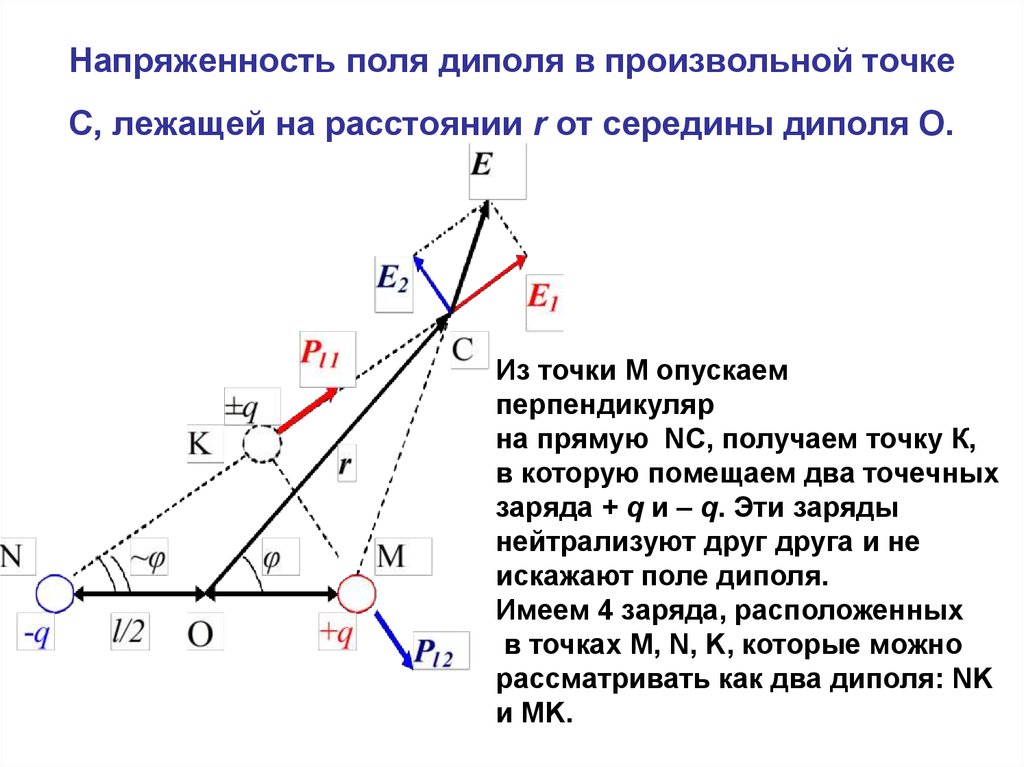
43. Напряженность поля диполя в произвольной точке С, лежащей на расстоянии r от середины диполя О.
Из точки М опускаемперпендикуляр
на прямую NC, получаем точку К,
в которую помещаем два точечных
заряда + q и – q. Эти заряды
нейтрализуют друг друга и не
искажают поле диполя.
Имеем 4 заряда, расположенных
в точках M, N, K, которые можно
рассматривать как два диполя: NK
и MK.
44. Напряженность поля диполя в произвольной точке С, лежащей на расстоянии r от середины диполя О.
l << r →Угол СNM ≈ φ→• Электрический момент
диполя NK:
pl1 q NK ql cos pl cos (1)
• Электрический момент
диполя MK:
pl 2 q KM ql sin pl sin (2)
pl1 pl 2
45.
Для диполя NK точка Слежит на его оси
1 2 pl1
E1
3 (3)
4 0 r
Для диполя МК точка С
лежит на перпендикуляре
1 pl 2
E2
3 (4)
4 0 r
E1 E2
pl1 pl 2
E
2
E1
2
E2
1
1
4 0 r
3
(2 pl1 ) pl 2
2
2
46.
Уравнения (1), (2) → (5):E
1
4 0 r
pl
4 0 r
2
2
4
cos
sin
3
pl
4 0 r
2
2
2
2
4
p
cos
p
sin
l
l
3
3 cos 1
2
3
47.
В предельных случаях:а) если , 0 0 то есть точка лежит на
оси диполя, то получим
2 pl
E
.
3
4 0 r
б) если , 90
то есть точка лежит на
перпендикуляре к оси диполя, то
получим
0
E
pl
4 0 r
3
.
48. Линейная, поверхностная и объемная плотности зарядов
Хотя электрический заряд дискретен,число его носителей в
макроскопических телах столь велико,
что можно ввести понятие плотности
заряда, использовав представление о
непрерывном «размазанном»
распределении заряда в пространстве.
49.
• Линейнаяплотность заряда:
dq Кл
,
dl м
заряд, приходящийся на единицу длины.
• Поверхностная
плотность заряда:
заряд, приходящийся на единицу
площади.
• Объемная
плотность заряда:
заряд, приходящийся на единицу
объема.
dq Кл
, 2
dS м
dq Кл
, 3
dV м
50. Линейная, поверхностная и объемная плотности зарядов
Полеdq dl
dq dS
dq dV
dE k
dE k
dE k
dl
r
2
l
dS
r
E k
dl
2
S
dV
r
E k
2
E k
V
r2
dS
r2
dV
r2
51. Напряженность и потенциал
В предыдущей теме было показано,
что взаимодействие между
покоящимися зарядами осуществляется
через электростатическое поле.
Описание электростатического поля мы
рассматривали с помощью
вектора
напряженности E , равного силе,
действующей в данной точке на
помещенный в неё пробный единичный
положительный заряд
F
E .
q
52.
• Существует и другой способ описанияполя – с помощью потенциала.
• Однако для этого необходимо сначала
доказать, что силы
электростатического поля
консервативны, а само поле
потенциально.
53.
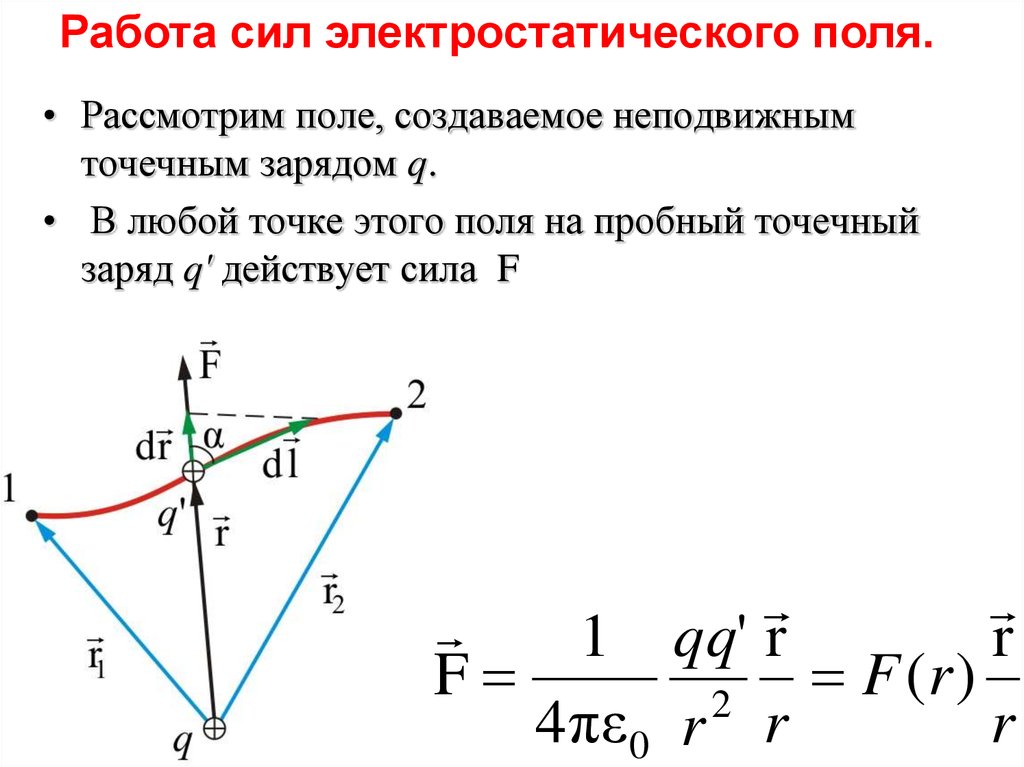
Работа сил электростатического поля.• Рассмотрим поле, создаваемое неподвижным
точечным зарядом q.
• В любой точке этого поля на пробный точечный
заряд q' действует сила F
1 qq' r
r
F
F
(
r
)
2
4πε0 r r
r
54.
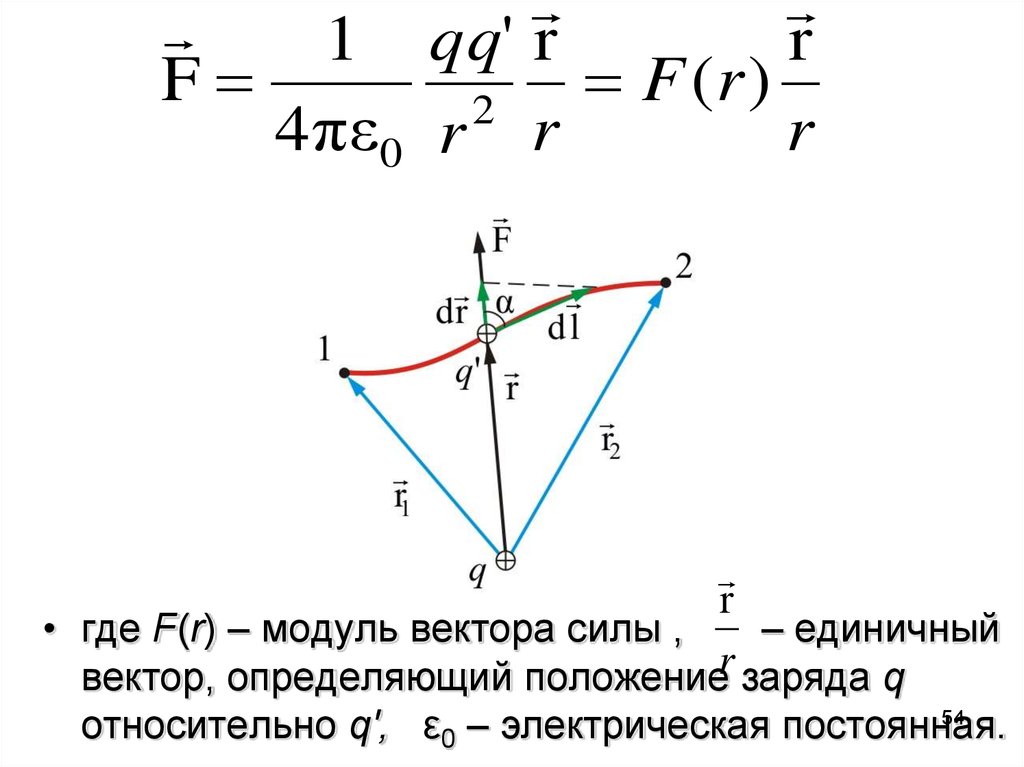
1 qq' rr
F
F
(
r
)
2
4πε0 r r
r
r
• где F(r) – модуль вектора силы ,
– единичный
вектор, определяющий положениеr заряда q
54
относительно q', ε0 – электрическая постоянная.
55.
• Для того, чтобы доказать, чтоэлектростатическое поле потенциально,
нужно доказать, что силы
электростатического поля
консервативны.
• Из раздела «Физические основы механики»
известно, что любое стационарное поле
центральных сил является
консервативным, т.е. работа сил этого
поля не зависит от формы пути, а только
от положения конечной и начальной точек.
56.
• Вычислим работу, которую совершаетэлектростатическое поле, созданное
зарядом q по перемещению заряда q' из
точки 1 в точку 2.
• Работа на отрезке пути dl равна:
1 qq'
dA Fdlcosα
dlcosα,
2
4πε0 r
• где dr – приращение радиус-вектора при
перемещении на dl; dr dl cosα,
qq'
dA
d
r
.
2
4πε0 r
57.
• Полная работа при перемещении източки 1 в точку 2 равна интегралу:
qq' dr qq' 1 r2 qq' 1 1
A12
.
2
4πε0 r1 r 4πε0 r r1 4πε0 r1 r2
r2
58.
• Работа электростатическихсил не зависит от формы
пути, а только лишь от
координат начальной и
конечной точек перемещения.
Следовательно, силы поля
консервативны, а само поле –
потенциально.
59.
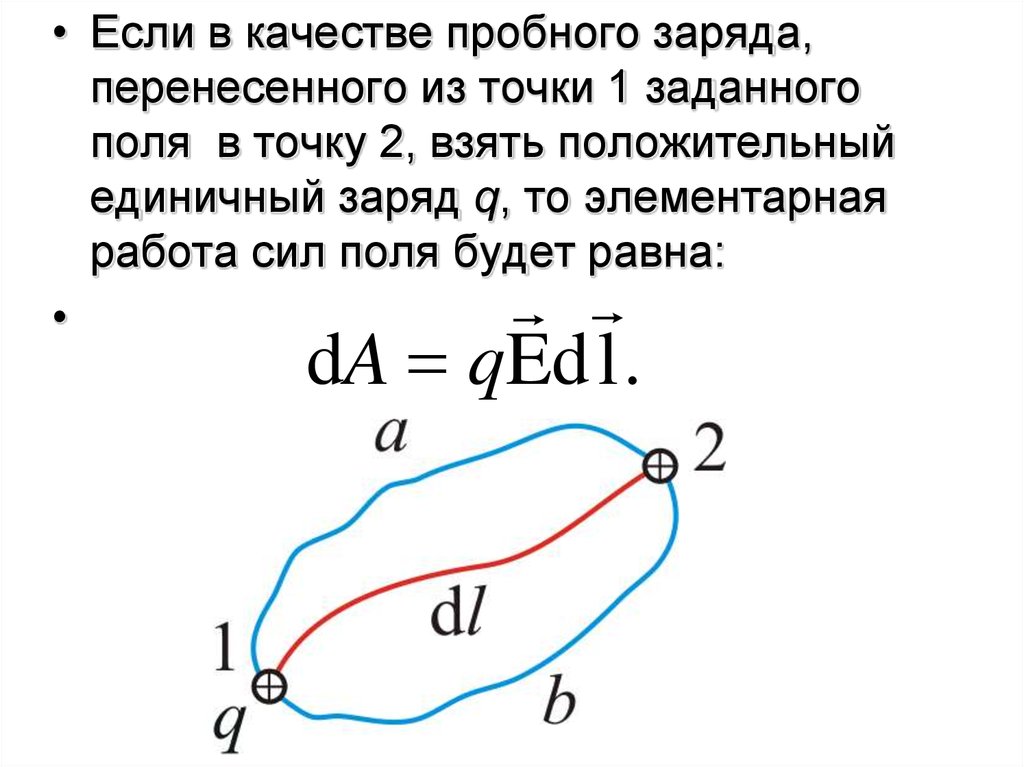
• Если в качестве пробного заряда,перенесенного из точки 1 заданного
поля в точку 2, взять положительный
единичный заряд q, то элементарная
работа сил поля будет равна:
dA qEd l .
60.
• Тогда вся работа равна:A
q
E
d
l
.
1
• Такой интеграл по замкнутому контуру
называется циркуляцией вектора E
• Из независимости линейного интеграла от
пути между двумя точками следует, что по
произвольному замкнутому пути:
2
E
d
l
0
.
• теорема о циркуляции вектора
E
.
61.
• Для доказательства теоремы разобьемпроизвольно замкнутый путь на две части:
1а2 и 2b1. Из сказанного выше следует, что
2
1
1
2
Edl Edl.
• (Интегралы по модулю равны, но знаки
противоположны). Тогда работа по
замкнутому пути:
2
1
A q Ed l q Ed l q Ed l 0.
1
2
62.
• Теорема о циркуляции позволяет сделать рядважных выводов, практически не прибегая к
расчетам.
• Рассмотрим простой пример, подтверждающий это
заключение.
• 1)Линии электростатического поля не могут
быть замкнутыми.
В самом деле, если это не так,
и какая-то линия E – замкнута, то, взяв
циркуляцию вдоль этой линии, мы сразу же придем
к противоречию
о циркуляции
с теоремой
Ed l 0 .
вектора E :
• А в данном случае направление интегрирования
в
одну сторону, поэтому циркуляция вектора E не
равна нулю.
63. Работа и потенциальная энергия
• Мы сделали важное заключение,что электростатическое поле
потенциально.
• Следовательно, можно ввести
функцию состояния, зависящую от
координат – потенциальную
энергию.
64.
• Исходя из принципа суперпозиции сил ,F Fk
k
• можно показать, что общая работа А
будет равна сумме работ каждой силы:
A Ak .
k
• Здесь каждое слагаемое не зависит от
формы пути, следовательно, не
зависит от формы пути и сумма.
65.
• Работу сил электростатического поляможно выразить через убыль
потенциальной энергии – разность двух функций
состояний:
A12 W1 W2 .
Это выражение для работы можно
переписать в виде:
qq'
qq'
A12
4πε0 r1
4πε0 r2
.
• Сопоставляя формулу (3.2.2) и (3.2.3), получаем
выражение для потенциальной энергии заряда
1 qq'
q' в поле заряда q:
W
4 0 r
66. Потенциал. Разность потенциалов
• Разные пробные заряды q',q'',… будутобладать в одной и той же точке поля
разными энергиями W', W'' и так далее.
Однако отношение W / q'пр. будет для всех
зарядов одним и тем же.
• Поэтому можно вести скалярную
величину, являющуюся энергетической
характеристикой поля – потенциал:
W
φ .
q'
67.
Wφ .
q'
• Из этого выражения следует, что
потенциал численно равен
потенциальной энергии, которой
обладает в данной точке поля
единичный положительный заряд.
68.
• Подставив в выражение для потенциалазначение потенциальной энергии,
получим выражение для
потенциала точечного заряда:
1 q
φ
.
4πε0 r
• Потенциал, как и потенциальная энергия,
определяют с точностью до постоянной
интегрирования.
69.
• физический смысл имеет непотенциал, а разность потенциалов,
поэтому договорились считать, что
потенциал точки, удаленной в
бесконечность, равен нулю.
• Когда говорят «потенциал такой-то
точки» – имеют в виду разность
потенциалов между этой точкой и
точкой, удаленной в бесконечность.
70.
• Другое определение потенциала:A
φ
q
или
A qφ
• т.е. потенциал численно равен работе,
которую совершают силы поля над
единичным положительным зарядом при
удалении его из данной точки в
бесконечность
• (или наоборот – такую же работу нужно
совершить, чтобы переместить
единичный положительный заряд из
бесконечности в данную точку поля).
• При этом φ 0 , если q > 0.
71.
• Если поле создается системой зарядов, то,используя принцип суперпозиции, получаем:
1
W
4πε0
qk q '
r .
k
k
• Тогда и для потенциала
1
φ
4 πε 0
qk
r
k
k
φ φ k или
k
• т.е. потенциал поля, создаваемый
системой зарядов, равен алгебраической
сумме потенциалов, создаваемых каждым
из зарядов в отдельности.
• А вот напряженности складываются при
наложении полей – векторно.
72.
• Выразим работу сил электростатическогополя через разность потенциалов между
начальной и конечной точками:
•A W W φ q φ q q φ φ
12
1
2
1
2
1
2
.
• Таким образом, работа над зарядом q равна
произведению заряда на убыль потенциала:
1
2
A q φ φ
qU ,
• где U – напряжение.
A qU
73.
• Формулу A q можно использовать дляустановления единиц потенциала:
за единицу φ принимают потенциал в
такой точке поля, для перемещения в
которую из бесконечности единичного
положительного заряда необходимо
совершить работу равную единице.
• В СИ единица потенциала 1 В 1 Дж/1 Кл
74.
Электрон - вольт (эВ) – это работа,совершенная силами поля над зарядом,
равным заряду электрона при прохождении
им разности потенциалов 1 В, то есть:
1 эВ 1,6 10
19
Кл В 1,6 10
19
Производными единицами эВ являются
МэВ, ГэВ и ТэВ:
1 МэВ = 106 эВ = 1,60 10 13 Дж,
1 ГэВ = 109 эВ = 1,60 10 10 Дж,
1 ТэВ = 1012 эВ = 1,60 10 7 Дж.
Дж.
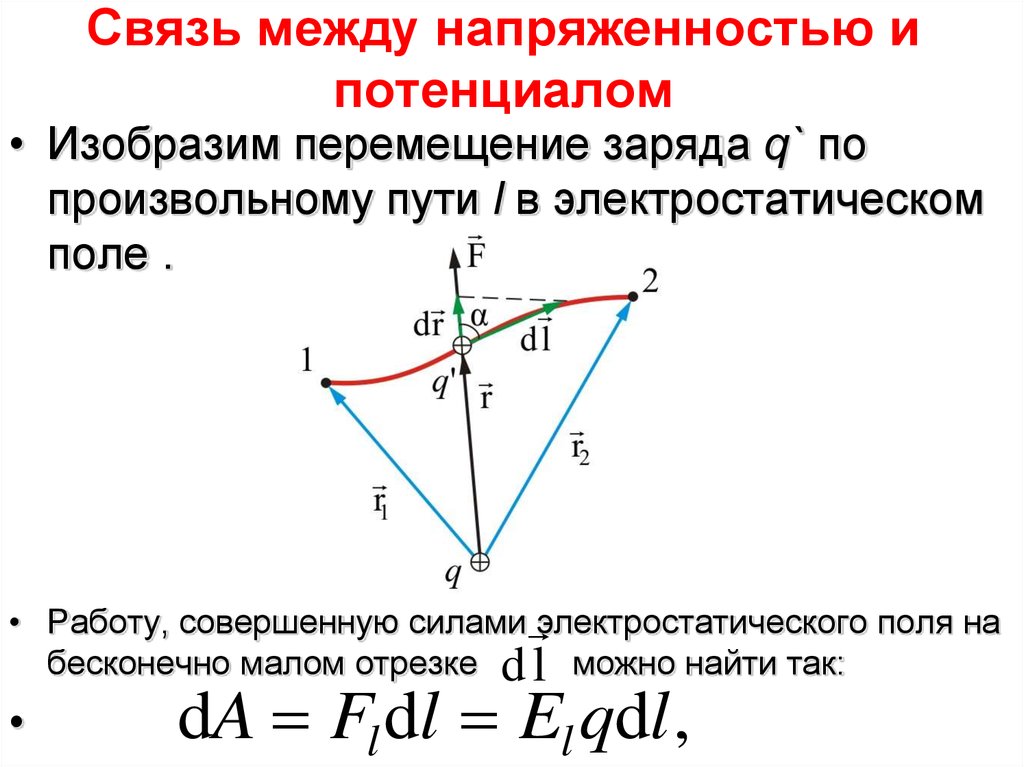
75. Связь между напряженностью и потенциалом
• Изобразим перемещение заряда q` попроизвольному пути l в электростатическом
поле .
• Работу, совершенную силами электростатического поля на
бесконечно малом отрезке d l можно найти так:
dA Fl dl El qdl ,
76.
dA Fl dl El qdl ,• С другой стороны, эта работа, равна
убыли потенциальной энергии заряда,
перемещенного на расстоянии dl:
dA qdφ; тогда
El qdl qdφ
• отсюда
dφ
El .
dl
77.
• Для ориентации dl (направлениеперемещения) в пространстве, надо знать
проекции на оси координат:
φ
φ
φ
E i
j k,
x
y
z
• Определение градиента: сумма первых
производных от какой-либо функции по
координатам есть градиент этой
φ φ
φ
функции
grad φ i
j k,
x
y
z
• gradφ – вектор, показывающий
направление наибыстрейшего
77
увеличения функции.
78.
• Коротко связь между E и φ записывается так:• или так:
E grad φ
E φ
(3.4.4)
(3.4.5)
• где (набла) означает символический
вектор, называемый оператором Гамильтона
• Знак минус говорит о том, что вектор
направлен в сторону уменьшения
потенциала электрического поля.
78
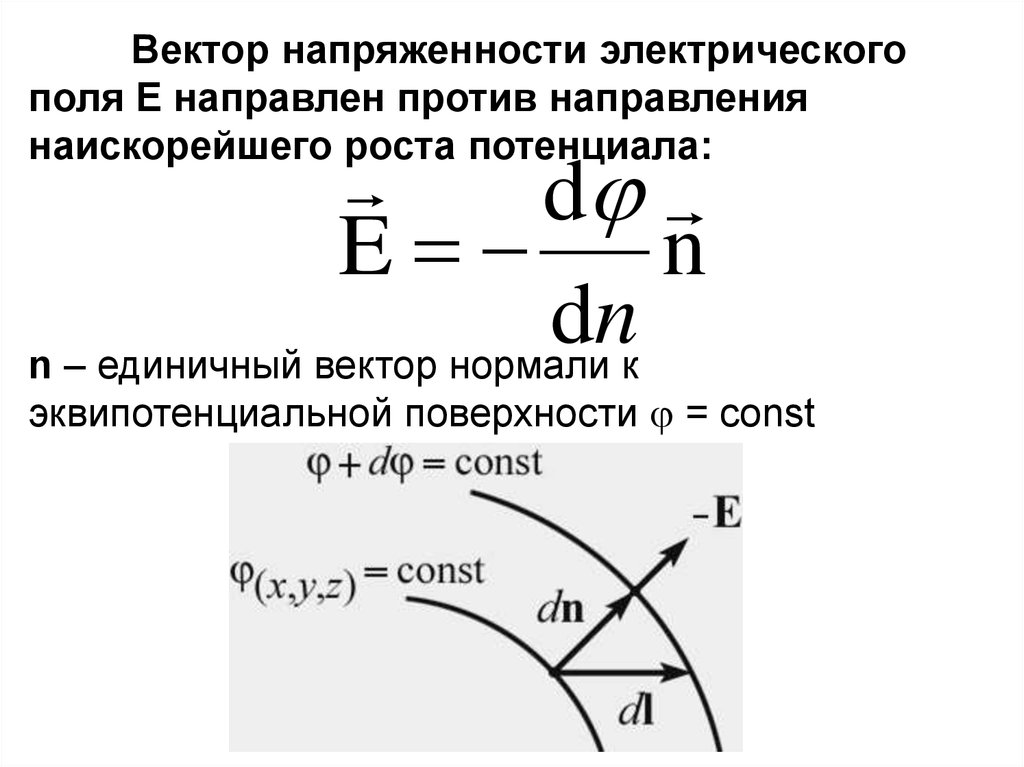
79.
Вектор напряженности электрическогополя Е направлен против направления
наискорейшего роста потенциала:
d
E
n
d
n
n – единичный вектор нормали к
эквипотенциальной поверхности = const
80. Безвихревой характер электростатического поля
Безвихревой характер
электростатического поля
Из условия E φ
следует одно важное
соотношение, а именно,
величина, векторного
произведения [ , E] для стационарных
электрических полей всегда равна нулю.
Действительно, по определению, имеем
,
i
j
k
i
j
k
[ , E]
φ 0
x y z x y z
φ φ φ
x y z x y z
• поскольку определитель содержит две одинаковые
строки.
81.
• Величина [ , E] называется ротором иливихрем
• Мы получаем важнейшее уравнение
электростатики:
(3.5.1)
rotE 0
электростатическое поле –
безвихревое.
81
82.
• Согласно теореме Стокса, присутствуетследующая связь между контурным и
поверхностным интегралами:
(
E
,
d
l
)
rot
E
d
S
0
L
S
• где контур L ограничивающий поверхность S
ориентация которой определяется
направлением
положительной
вектора
нормали n : dS ndS
• Поэтому работа при перемещении заряда
по любому замкнутому пути в
82
электростатическом поле равна нулю.
83. 3.6. Силовые линии и эквипотенциальные поверхности
3.6. Силовые линии и
эквипотенциальные поверхности
Направление силовой линии (линии напряженности)
в
каждой точке совпадает с направлением E .
• Отсюда следует, что напряженность равна
разности потенциалов U на единицу длины силовой
линии.
• Именно вдоль силовой линии происходит максимальное
изменение потенциала. Поэтому всегда можно определить
между двумя точками, измеряя U между ними,
причем тем точнее, чем ближе точки.
• В однородном электрическом поле силовые линии –
прямые. Поэтому здесь определить E наиболее просто:
(3.6.1)
φ
U
E
l
83
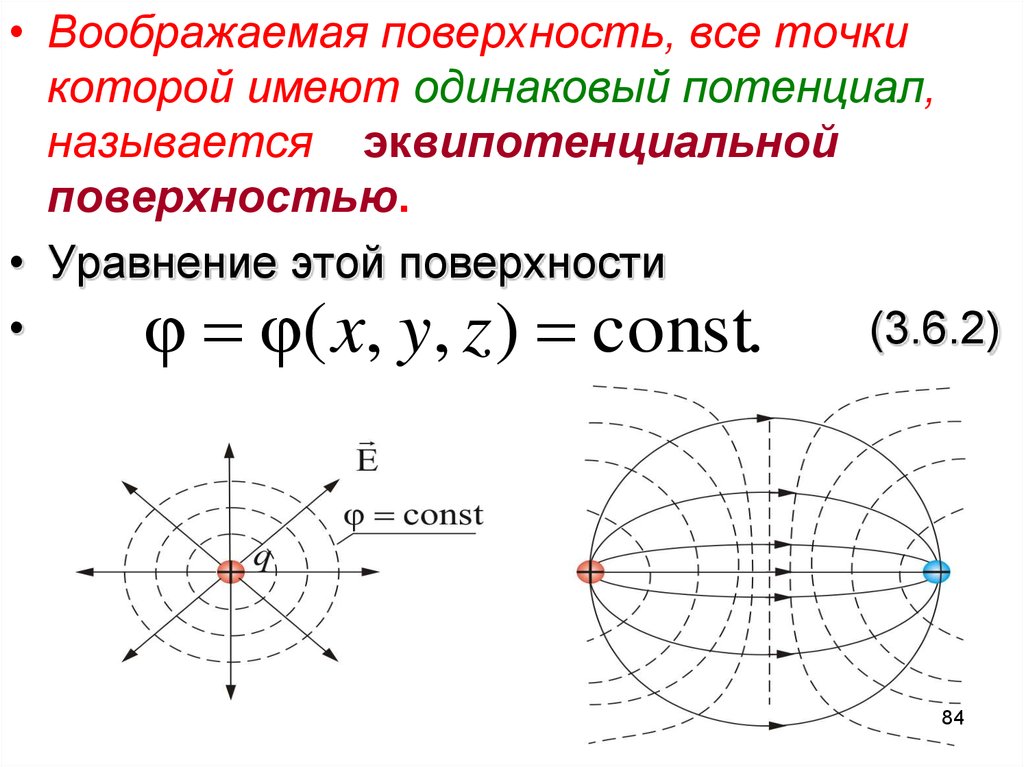
84.
• Воображаемая поверхность, все точкикоторой имеют одинаковый потенциал,
называется эквипотенциальной
поверхностью.
• Уравнение этой поверхности
φ φ( x, y, z ) const. (3.6.2)
84
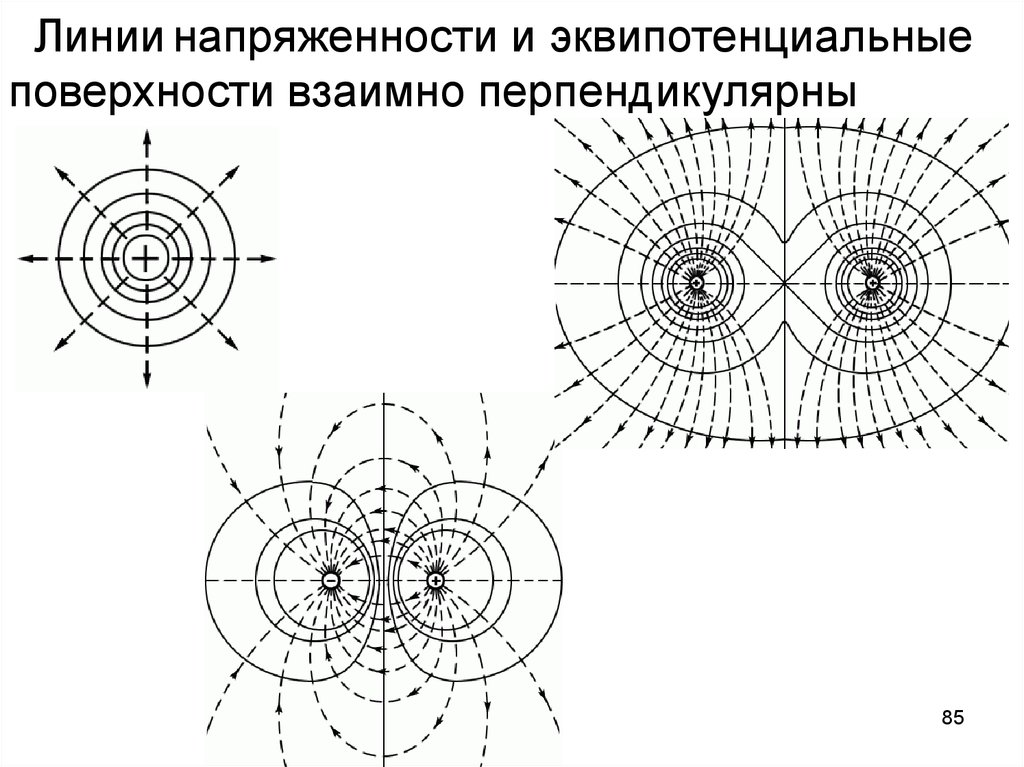
85.
Линии напряженности и эквипотенциальныеповерхности взаимно перпендикулярны
85
86.
E grad φ• Формула
выражает связь
потенциала с напряженностью и позволяет
по известным значениям φ найти
напряженность поля в каждой точке.
• Можно решить и обратную
задачу, т.е. по
известным значениям E в каждой точке
поля найти разность потенциалов между
двумя произвольными точками поля.
φ1 φ 2 (E, d l ).
2
1
86
87.
φ1 φ 2 (E, d l ).2
1
• Интеграл можно брать по любой линии,
соединяющие точку 1 и точку 2, ибо работа
сил поля не зависит от пути.
• Для обхода по замкнутому
контуру φ1 φ 2
получим:
(E, d l ) 0,
• т.е. пришли к известной нам теореме о
циркуляции вектора напряженности:
циркуляция вектора напряженности
электростатического поля вдоль любого
замкнутого контура равна нулю.
Поле, обладающее этим свойством, называется потенциальным.
87
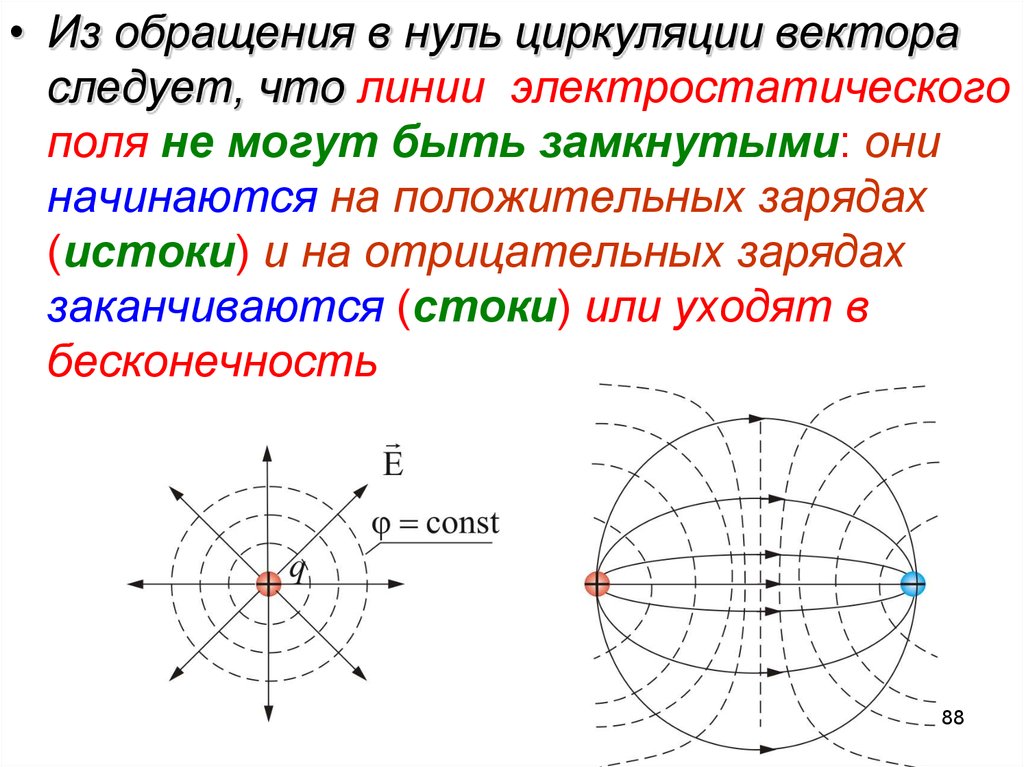
88.
• Из обращения в нуль циркуляции вектораследует, что линии электростатического
поля не могут быть замкнутыми: они
начинаются на положительных зарядах
(истоки) и на отрицательных зарядах
заканчиваются (стоки) или уходят в
бесконечность
88
89.
Там, где расстояние между эквипотенциальными поверхностямимало, напряженность поля наибольшая. Наибольшее электрическое поле в
воздухе при атмосферном давлении достигает около 106 В/м.
89
90. 3.7. Расчет потенциалов простейших электростатических полей
• Рассмотрим несколько примероввычисления разности потенциалов между
точками поля, созданного некоторыми
заряженными телами
90
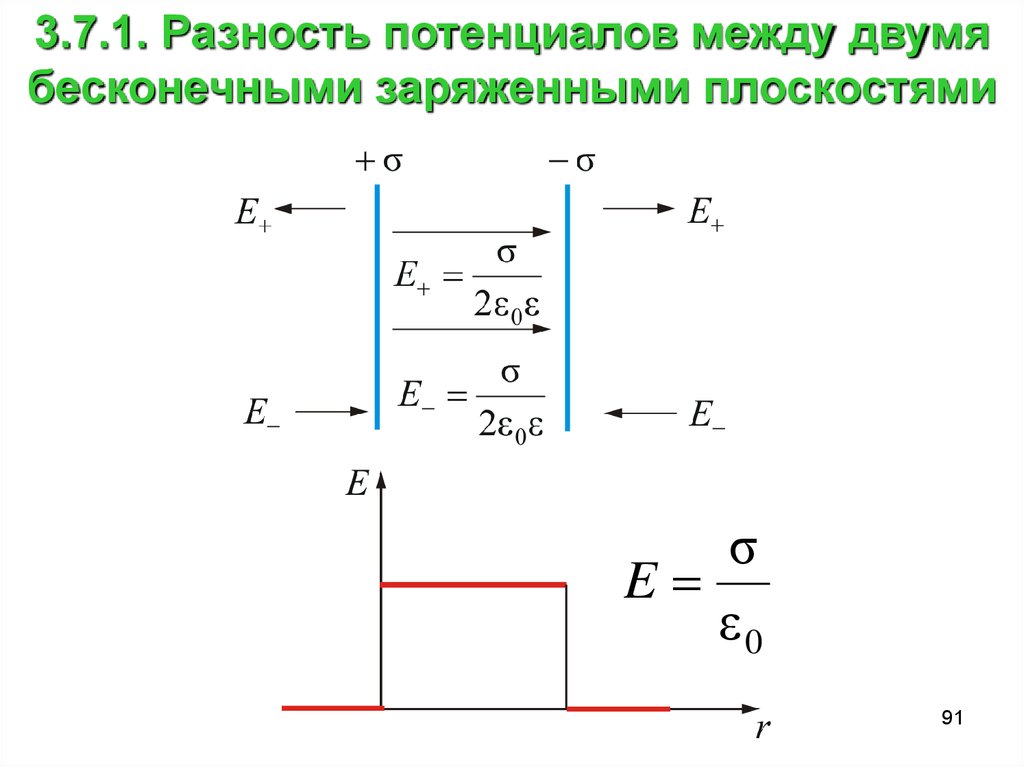
91.
3.7.1. Разность потенциалов между двумябесконечными заряженными плоскостями
σ
E
ε0
91
92.
• Мы показали, что напряженность связана спотенциалом
dφ
E
, отсюда
d
l
dφ Edl
σ
• где E
– напряженность
ε0
электростатического поля между
заряженными плоскостями
• σ = q/S – поверхностная плотность заряда.
92
93.
Чтобы получить выражение для
потенциала между плоскостями,
проинтегрируем выражение dφ
2
Edl
x2
σ
dφ ε 0 dx;
1
x1
σ
φ 2 φ1 x2 x1
ε0
При x1 = 0 и x2 = d
σd
φ 2 φ1
ε0
(3.7.3)
93
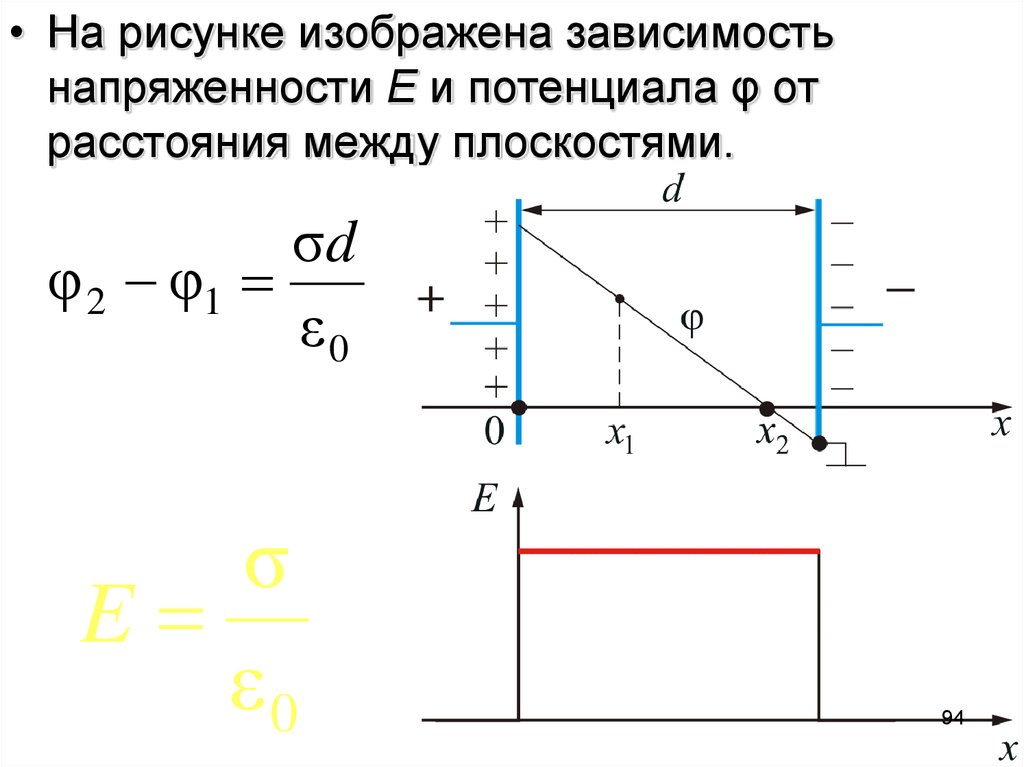
94.
• На рисунке изображена зависимостьнапряженности E и потенциала φ от
расстояния между плоскостями.
σd
φ 2 φ1
ε0
σ
E
ε0
94
95. 3.7.2. Разность потенциалов между точками поля, образованного бесконечно длинной цилиндрической поверхностью
• С помощью теоремы ОстроградскогоГаусса мы показали, что0
внутри
цилиндра,
т.к.
там
нет
зарядов
λ
q
E
или
на поверхности цилиндра
2
πε
R
2
πε
Rl
0
0
λ
q
или
вне цилиндра.
95
2
πε
r
2
πε
rl
0
0
96.
• Тогда,т.к.dφ Edr;
2
λ
dφ 2 πε 0
1
r2
r1
dr
r
• отсюда следует, что разность потенциалов
в произвольных точках 1 и 2 будет равна:
λ
r2
q
r2
ln
ln
• φ 2 φ1
2πε0 r1
2πε0l r1
1
λ
ln
const
внутри
и
на
поверхност
и
2πε
R
0
φ
λ ln r вне цилиндра.
96
2πε0 R
97.
λln
2πε
0
φ
λ ln
2πε0
1
const внутри и на поверхн
R
r
вне цилиндра.
R
97
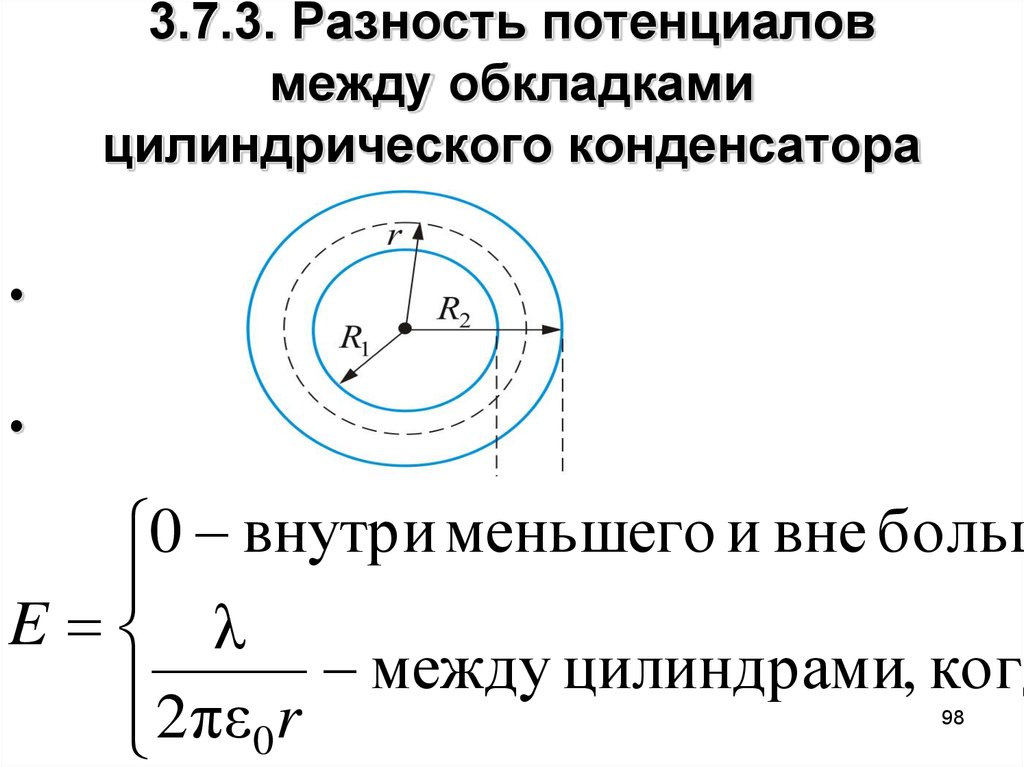
98. 3.7.3. Разность потенциалов между обкладками цилиндрического конденсатора
0 внутри меньшего и вне больш
E λ
между
цилиндрами
,
когд
2πε r
0
98
99.
• Т.к.dφ Edr
, то
λ
r2
φ 2 φ1
ln
2πε0 r1
R2
λ
ln
const
внутри
меньшего
цили
2 πε
R1
0
r
λ
φ
ln между цилиндрами ( R1 r R
2
πε
R
0
1
0 вне цилиндров.
99
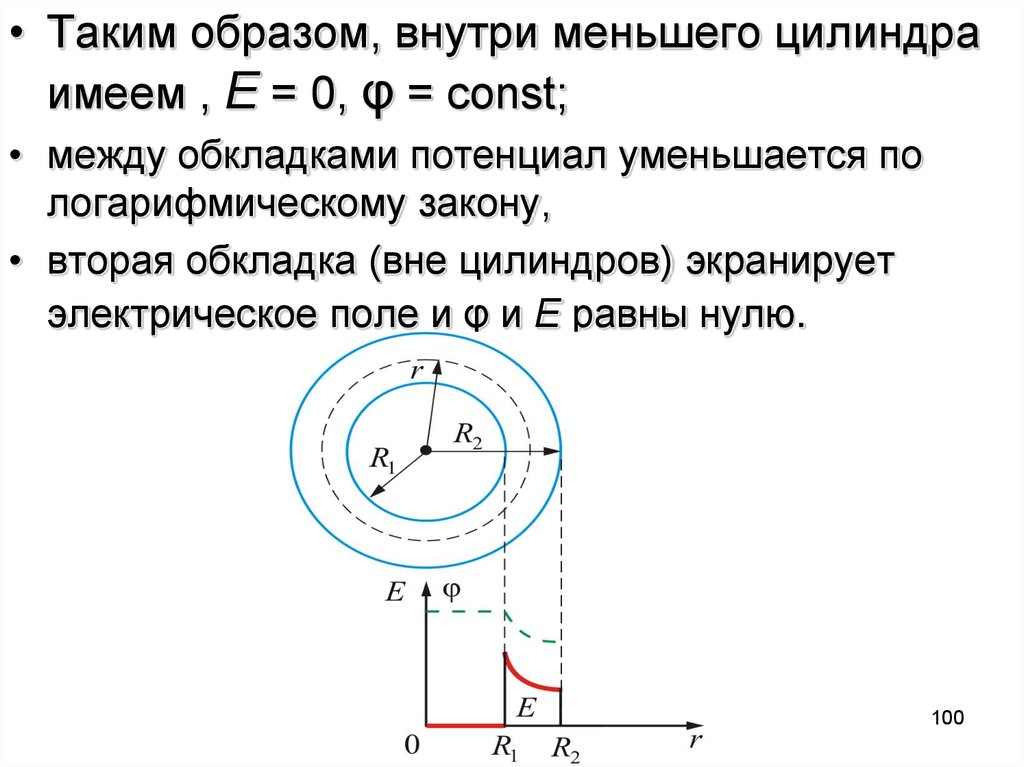
100.
• Таким образом, внутри меньшего цилиндраимеем , Е = 0, φ = const;
• между обкладками потенциал уменьшается по
логарифмическому закону,
• вторая обкладка (вне цилиндров) экранирует
электрическое поле и φ и Е равны нулю.
100
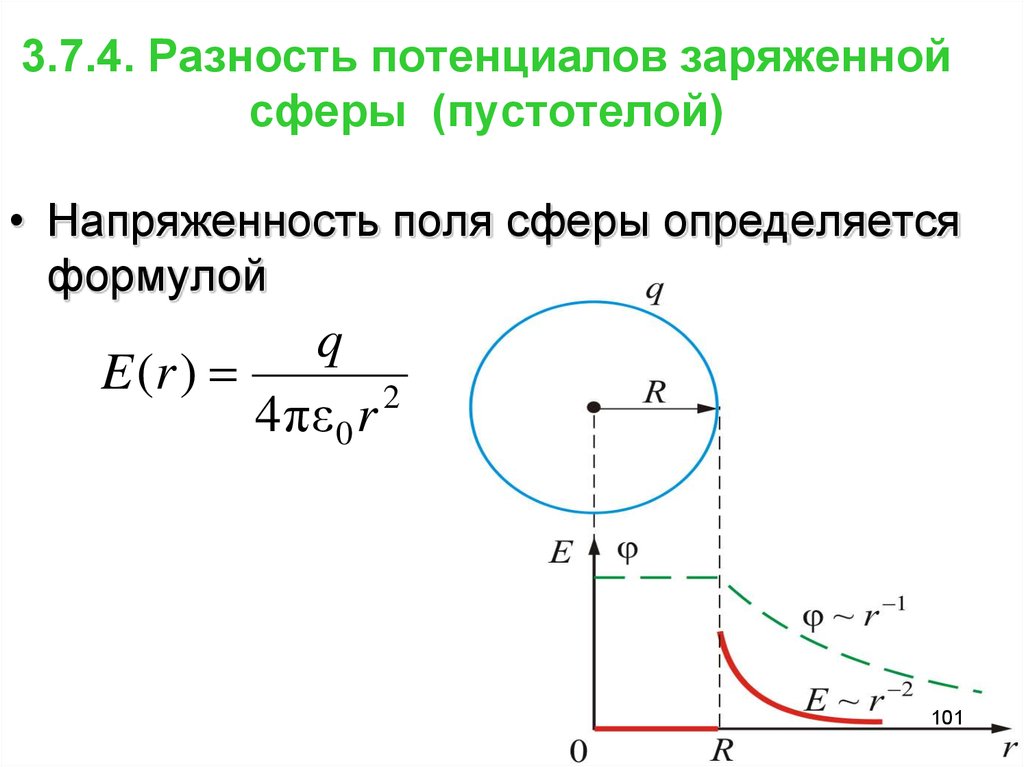
101. 3.7.4. Разность потенциалов заряженной сферы (пустотелой)
• Напряженность поля сферы определяетсяформулой
q
E (r )
2
4 πε 0 r
101
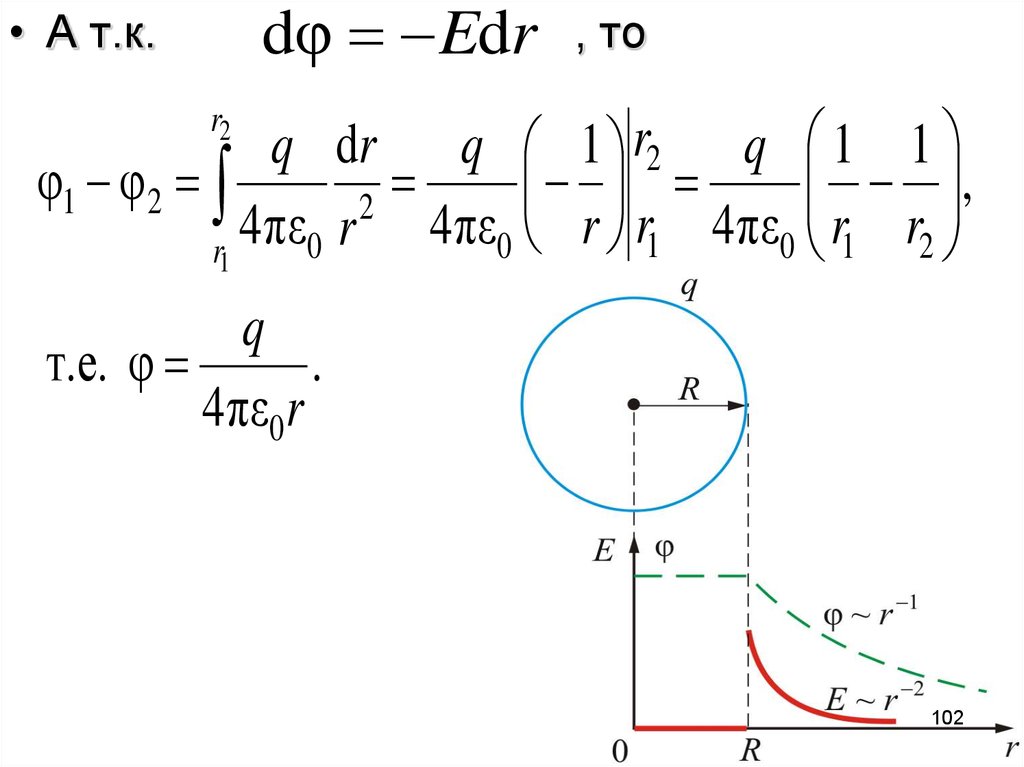
102.
dφ Edr• А т.к.
, то
q dr q 1 r2 q 1 1
φ1 φ2
,
2
r
4
πε
4
πε
r
4
πε
r
r
r
1
0
0
0
1
2
r1
r2
q
т.е. φ
.
4πε0r
102
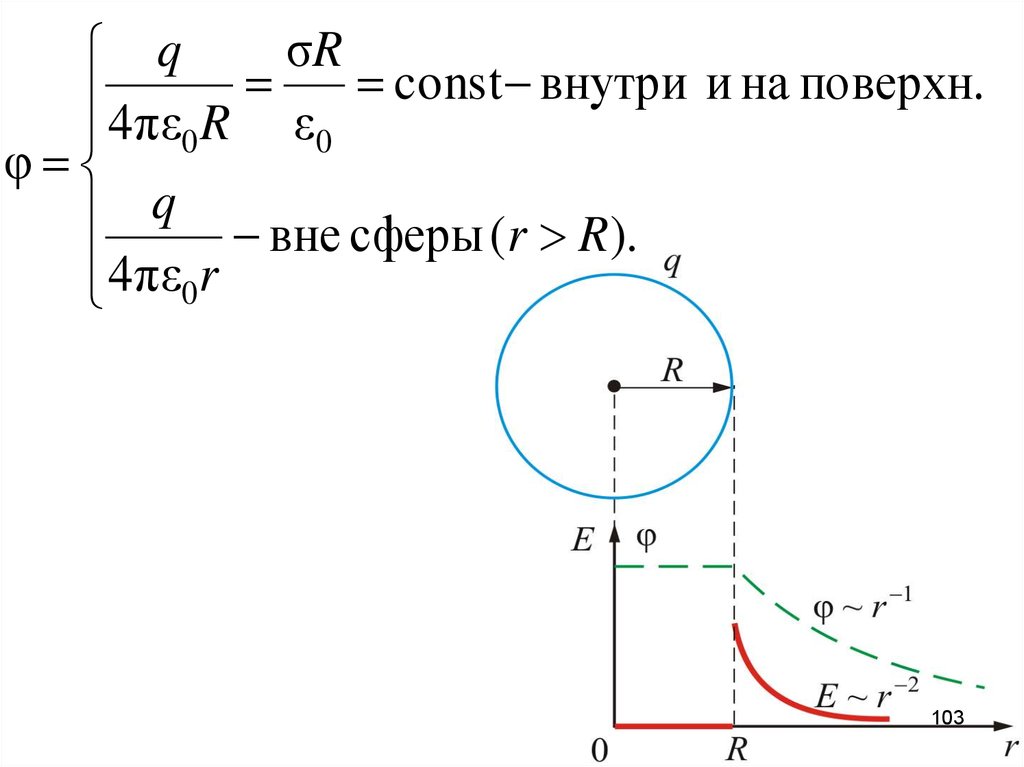
103.
σRq
const
внутри
и
на
поверхн.
4πε R ε
0
0
φ
q вне сферы (r R).
4πε0r
103
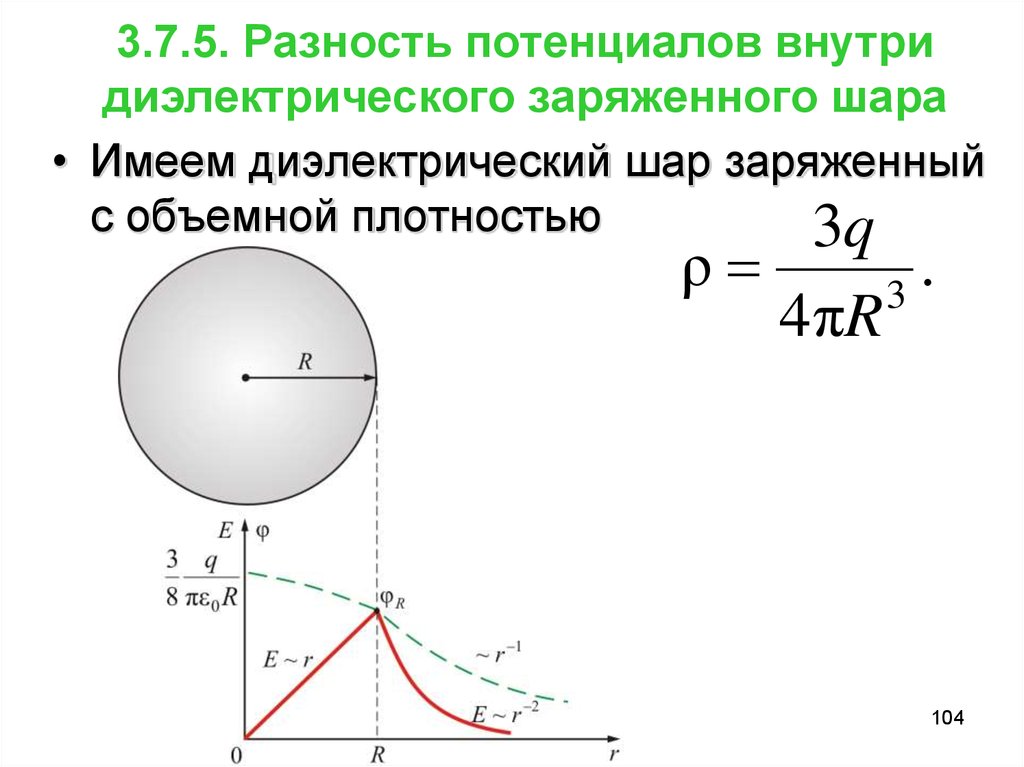
104. 3.7.5. Разность потенциалов внутри диэлектрического заряженного шара
• Имеем диэлектрический шар заряженныйс объемной плотностью
3q
ρ
4 πR
.
3
104
105.
• Напряженность поля шара, вычисленнаяс помощью теоремы ОстроградскогоГаусса:
• qr
ρr
внутри шара (r R )
3
3
ε
4
πε
R
0
0
q
E•
на
поверхност
и
шара
(
r
R
)
2
4 πε0 R
q
вне шара (r R ).
2
4 πε0 r
105
106.
• Отсюда найдем разность потенциаловшара:
2
2
ρ
ρ 2
φ 2 φ1 Edr
1
rdr
r2
3ε 0
6ε 0
2
r1
1
или
φ1 φ 2
2
r1 )
.
3
4πε0 2R
2
q(r2
106
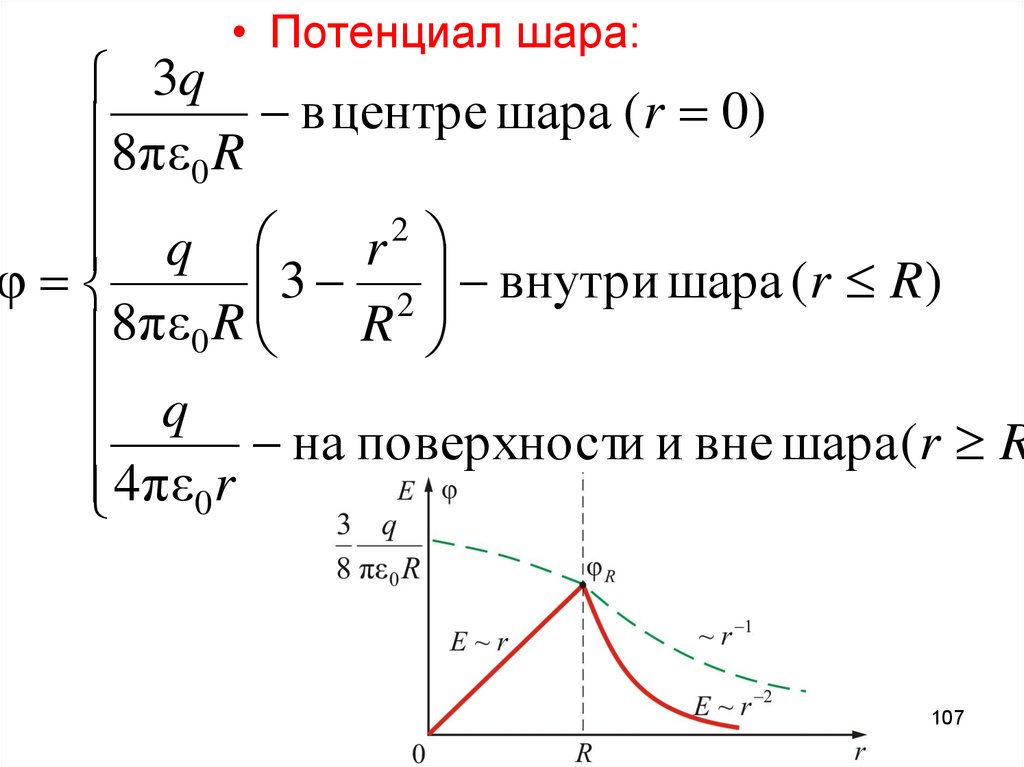
107.
• Потенциал шара:3q
в
центре
шара
(
r
0
)
8πε R
0
2
q
r
3 2 внутри шара (r R)
φ
8
πε
R
R
0
q
на поверхности и вне шара (r R
4 πε0 r
107
108.
• Из полученных соотношений можносделать следующие выводы:
• С помощью теоремы Гаусса
сравнительно просто можно
рассчитать Е и φ от различных
заряженных поверхностей.
• Напряженность поля в вакууме
изменяется скачком при переходе
через заряженную поверхность.
• Потенциал поля – всегда непрерывная
108
функция координат.






































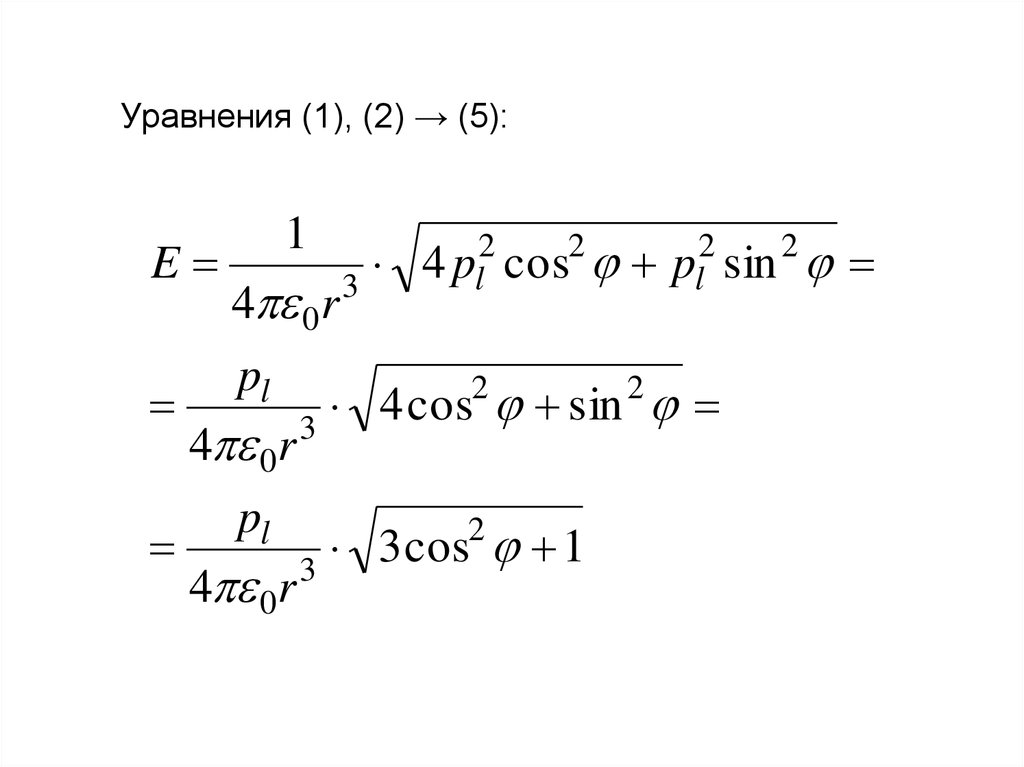













































 physics
physics








