Similar presentations:
Напряженность и потенциал
1. Напряженность и потенциал
В предыдущей теме было показано, что
взаимодействие между покоящимися
зарядами осуществляется через
электростатическое поле. Описание
электростатического поля мы
рассматривали с помощью
вектора
напряженностиE , равного силе,
действующей в данной точке на
помещенный в неё пробный единичный
F
положительный заряд
E .
q
1
2.
• Существует и другой способ описанияполя – с помощью потенциала.
• Однако для этого необходимо сначала
доказать, что силы электростатического
поля консервативны, а само поле
потенциально.
2
3.
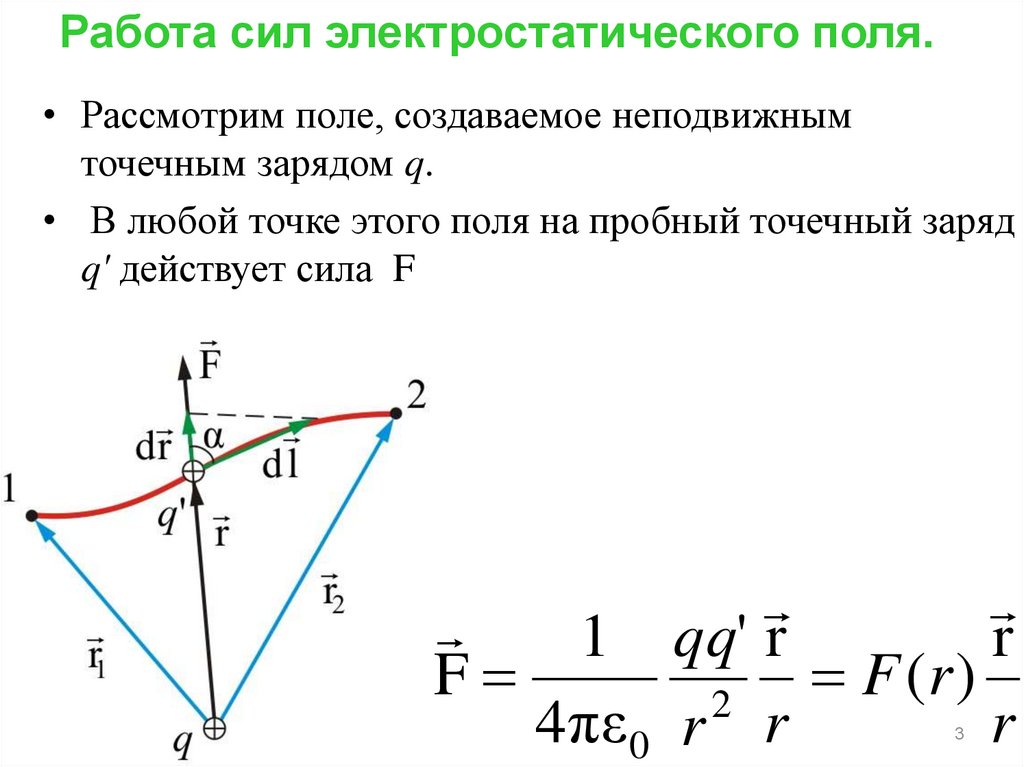
Работа сил электростатического поля.• Рассмотрим поле, создаваемое неподвижным
точечным зарядом q.
• В любой точке этого поля на пробный точечный заряд
q' действует сила F
1 qq' r
r
F
F
(
r
)
2
4πε0 r r
r
3
4.
1 qq' rr
F
F
(
r
)
2
4πε0 r r
r
r
– единичный
r
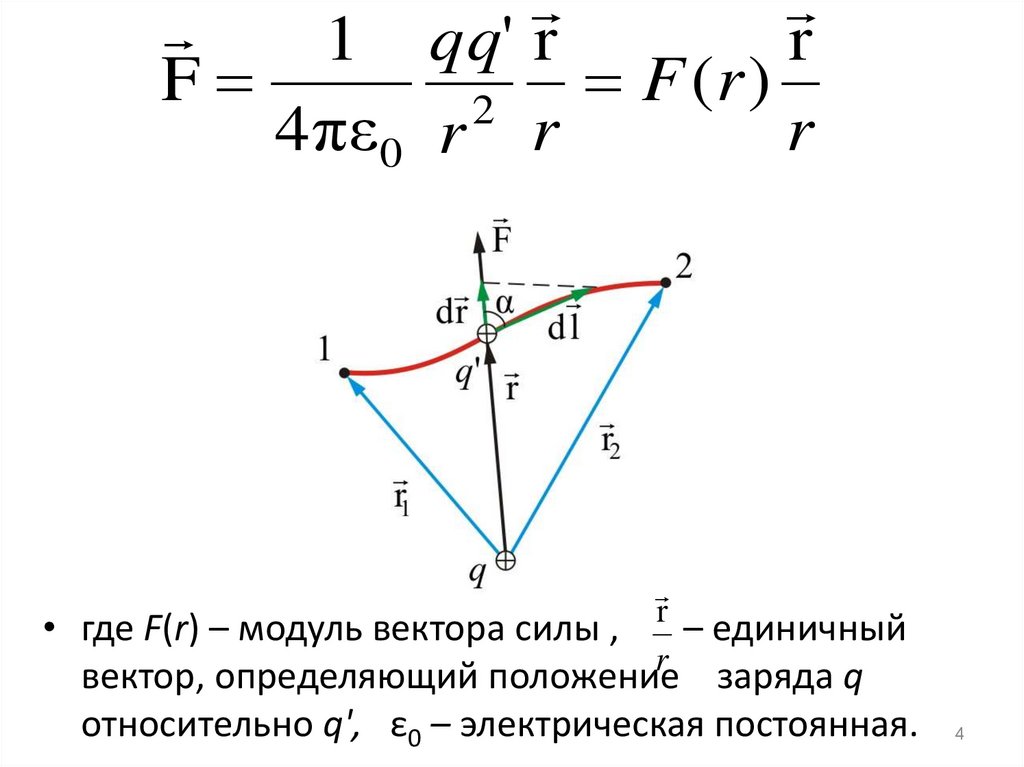
• где F(r) – модуль вектора силы ,
вектор, определяющий положение заряда q
относительно q', ε0 – электрическая постоянная.
4
5.
• Для того, чтобы доказать, чтоэлектростатическое поле потенциально,
нужно доказать, что силы электростатического
поля консервативны.
• Из раздела «Физические основы механики»
известно, что любое стационарное поле
центральных сил является консервативным,
т.е. работа сил этого поля не зависит от
формы пути, а только от положения конечной
и начальной точек.
5
6.
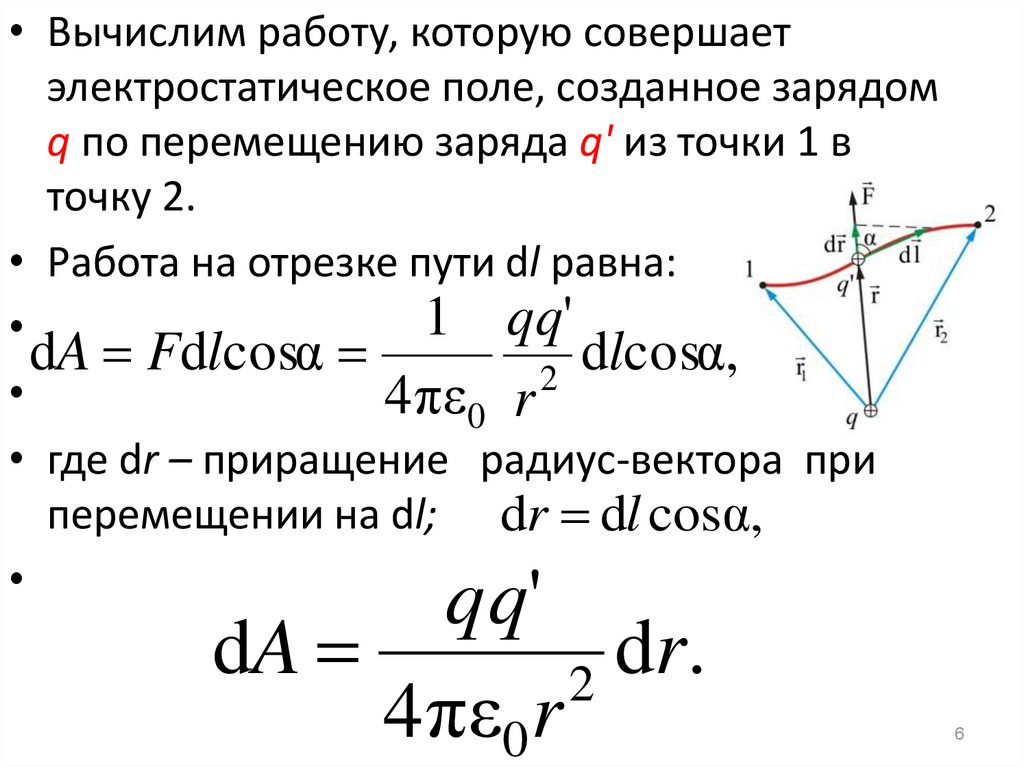
• Вычислим работу, которую совершаетэлектростатическое поле, созданное зарядом
q по перемещению заряда q' из точки 1 в
точку 2.
• Работа на отрезке пути dl равна:
1 qq'
dA Fdlcosα
dlcosα,
2
4πε0 r
• где dr – приращение радиус-вектора при
перемещении на dl; dr dl cosα,
qq'
dA
d
r
.
2
4πε0 r
6
7.
• Полная работа при перемещении из точки 1в точку 2 равна интегралу:
qq' dr qq' 1 r2 qq' 1 1
A12
.
2
4πε0 r1 r 4πε0 r r1 4πε0 r1 r2
r2
7
8.
• Работа электростатических силне зависит от формы пути, а
только лишь от координат
начальной и конечной точек
перемещения. Следовательно,
силы поля консервативны, а само
поле – потенциально.
8
9.
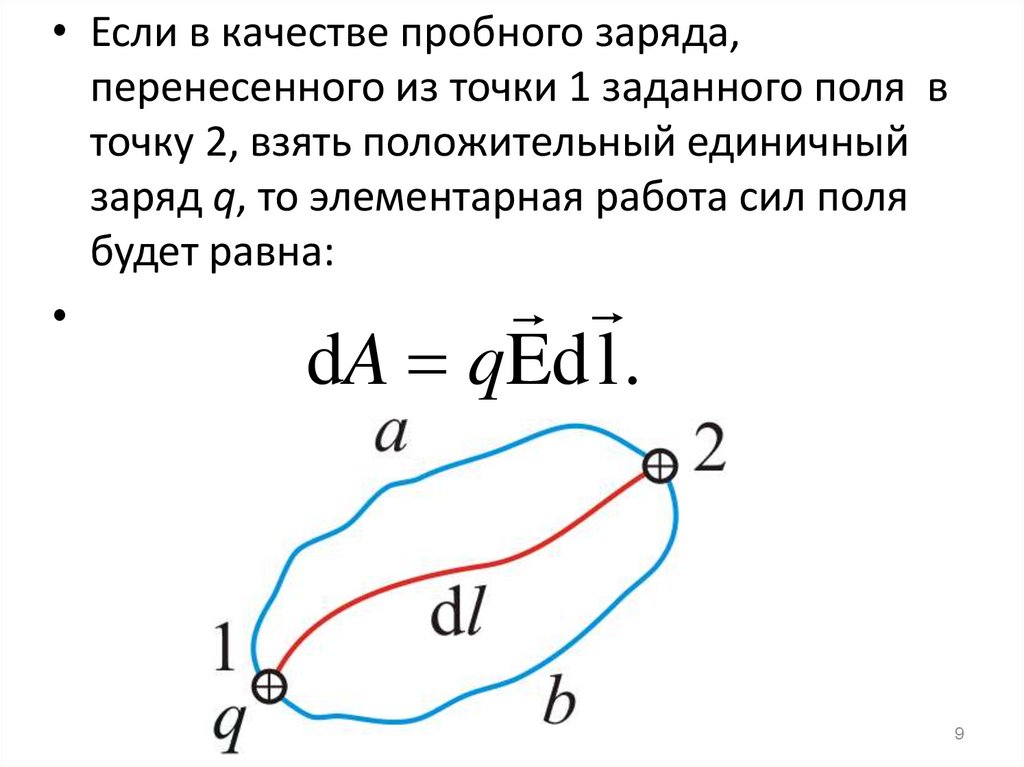
• Если в качестве пробного заряда,перенесенного из точки 1 заданного поля в
точку 2, взять положительный единичный
заряд q, то элементарная работа сил поля
будет равна:
dA qEd l .
9
10.
• Тогда вся работа равна:A
q
E
d
l
.
1
• Такой интеграл по замкнутому контуру
называется циркуляцией вектора
E
• Из независимости линейного интеграла от пути
между двумя точками следует, что по
произвольному замкнутому пути:
2
E
d
l
0
.
теорема о циркуляции вектора E
.
10
11.
• Для доказательства теоремы разобьемпроизвольно замкнутый путь на две части: 1а2 и
2b1. Из сказанного выше следует, что
2
1
1
2
Edl Edl.
• (Интегралы по модулю равны, но знаки
противоположны). Тогда работа по замкнутому
пути:
2
1
A q Ed l q Ed l q Ed l 0.
1
2
11
12.
• Теорема о циркуляции позволяет сделать ряд важныхвыводов, практически не прибегая к расчетам.
• Рассмотрим простой пример, подтверждающий это
заключение.
• 1)Линии электростатического поля не могут быть
замкнутыми. В самом деле, если это не так, и какая-то
линия E – замкнута, то, взяв циркуляцию вдоль этой
линии, мы сразу же придем к противоречию
с
теоремой о циркуляции вектора E :
Ed l 0.
• А в данном случае направление интегрирования в одну
сторону, поэтому циркуляция вектора E не равна нулю.
12
13. Работа и потенциальная энергия
• электростатическое полепотенциально.
• Следовательно, можно ввести
функцию состояния, зависящую от
координат – потенциальную
энергию.
13
14.
• Исходя из принципа суперпозиции сил ,F Fk
k
• можно показать, что общая работа А будет
равна сумме работ каждой силы:
A Ak .
k
• Здесь каждое слагаемое не зависит от
формы пути, следовательно, не зависит от
формы пути и сумма.
14
15.
• Работу сил электростатического поля можновыразить через убыль потенциальной энергии
– разность двух функций состояний:
A12 W1 W2 .
Это выражение для работы можно переписать в
виде:
qq'
qq'
A
.
12
4πε0 r1
4πε0 r2
• Сопоставляя формулу получаем выражение для
потенциальной энергии заряда q' в поле заряда q:
1
qq'
W
4 0 r
15
16. Потенциал. Разность потенциалов
• Разные пробные заряды q',q'',… будут обладать водной и той же точке поля разными энергиями
W', W'' и так далее. Однако отношение W / q'пр.
будет для всех зарядов одним и тем же.
• Поэтому можно вести скалярную величину,
являющуюся энергетической
характеристикой поля – потенциал:
W
φ .
q'
16
17.
• Подставив в выражение для потенциалазначение потенциальной энергии , получим
выражение для
потенциала
точечного заряда:
1 q
φ
.
4 πε 0 r
• Потенциал, как и потенциальная энергия,
определяют с точностью до постоянной
интегрирования.
17
18.
• физический смысл имеет не потенциал, аразность потенциалов, поэтому
договорились считать, что потенциал
точки, удаленной в бесконечность,
равен нулю.
• Когда говорят «потенциал такой-то
точки» – имеют в виду разность
потенциалов между этой точкой и
точкой, удаленной в бесконечность.
18
19.
• Другое определение потенциала:A
φ
q
или
A qφ
• т.е. потенциал численно равен работе,
которую совершают силы поля над единичным
положительным зарядом при удалении его из
данной точки в бесконечность
• (или наоборот – такую же работу нужно
совершить, чтобы переместить единичный
положительный заряд из бесконечности в
данную точку поля).
• При этом φ 0 , если q > 0.
19
20.
• Если поле создается системой зарядов, то,используя принцип суперпозиции, получаем:
1
W
4πε0
qk q '
r .
k
k
• Тогда и для потенциала
1
φ
4 πε 0
φ φ k или
qk
r
k
k
k
• т.е. потенциал поля, создаваемый системой
зарядов, равен алгебраической сумме
потенциалов, создаваемых каждым из зарядов
в отдельности.
• А вот напряженности складываются при
наложении полей – векторно.
20
21.
• Выразим работу сил электростатического полячерез разность потенциалов между начальной и
конечной точками:
A12 W1 W2 φ1q φ 2 q q φ1 φ 2 .
• Таким образом, работа над зарядом q равна
произведению заряда на убыль потенциала:
1
2
A q φ φ
qU ,
• где U – напряжение.
A qU
21
22.
• Формулу A q можно использовать дляустановления единиц потенциала:
за единицу потенциала принимают потенциал
в такой точке поля, для перемещения в
которую из бесконечности единичного
положительного заряда необходимо
совершить работу равную единице.
• В СИ единица потенциала
1 В 1 Дж/1 Кл
22
23.
Электрон - вольт (эВ) – это работа,совершенная силами поля над зарядом,
равным заряду электрона при прохождении
им разности потенциалов 1 В, то есть:
1 эВ 1,6 10
19
Кл В 1,6 10
19
Дж.
Производными единицами эВ являются
МэВ, ГэВ и ТэВ:
1 МэВ = 106 эВ = 1,60 10 13 Дж,
1 ГэВ = 109 эВ = 1,60 10 10 Дж,
1 ТэВ = 1012 эВ = 1,60 10 7 Дж.
23
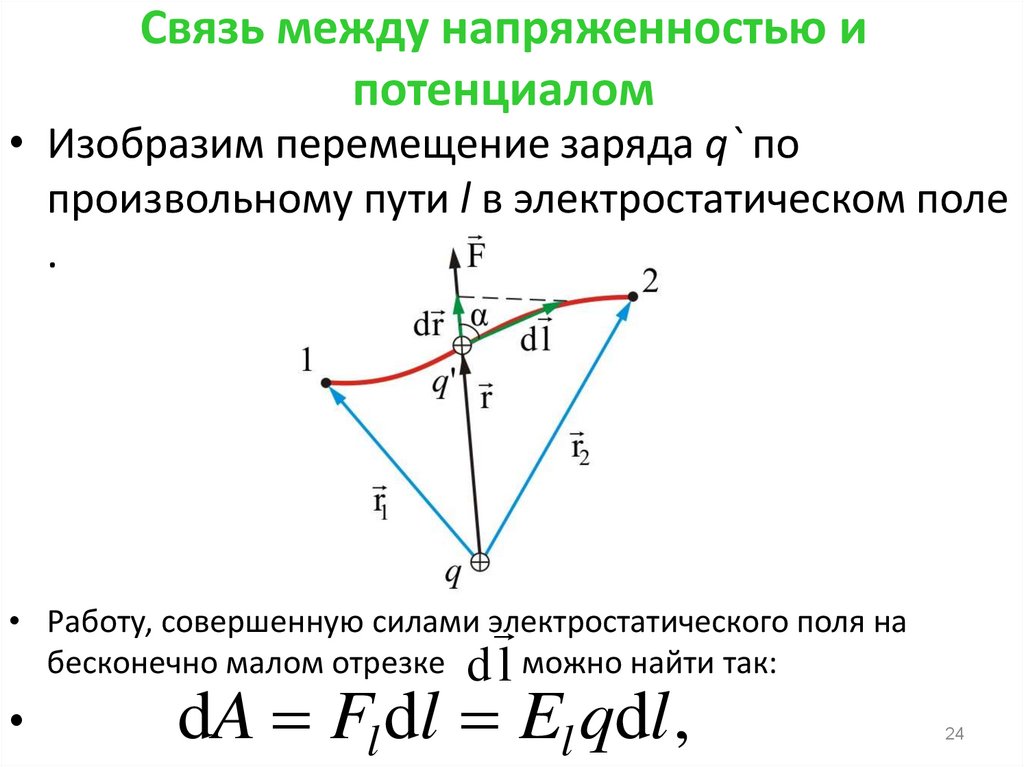
24. Связь между напряженностью и потенциалом
• Изобразим перемещение заряда q` попроизвольному пути l в электростатическом поле
.
• Работу, совершенную силами электростатического
поля на
бесконечно малом отрезке d l можно найти так:
dA Fl dl El qdl ,
24
25.
dA Fl dl El qdl ,• С другой стороны, эта работа, равна убыли
потенциальной энергии заряда,
перемещенного на расстоянии dl:
dA qdφ; тогда
El qdl qdφ
• отсюда
dφ
El .
dl
25
26.
• Для ориентации dl (направление перемещения) впространстве, надо знать проекции на оси
координат:
φ
φ
φ
E i
j k,
x
y
z
• Определение градиента: сумма первых
производных от какой-либо функции по
координатам есть градиент этой функции
φ φ
φ
grad φ i
j k,
x
y
z
gradφ – вектор, показывающий направление
наибыстрейшего увеличения функции.
26
27.
• Коротко связь междуE и φ записывается так:• или так:
E grad φ
E φ
• где (набла) означает символический вектор,
называемый оператором Гамильтона
• Знак минус говорит о том, что вектор направлен в
сторону уменьшения потенциала электрического
поля.
27
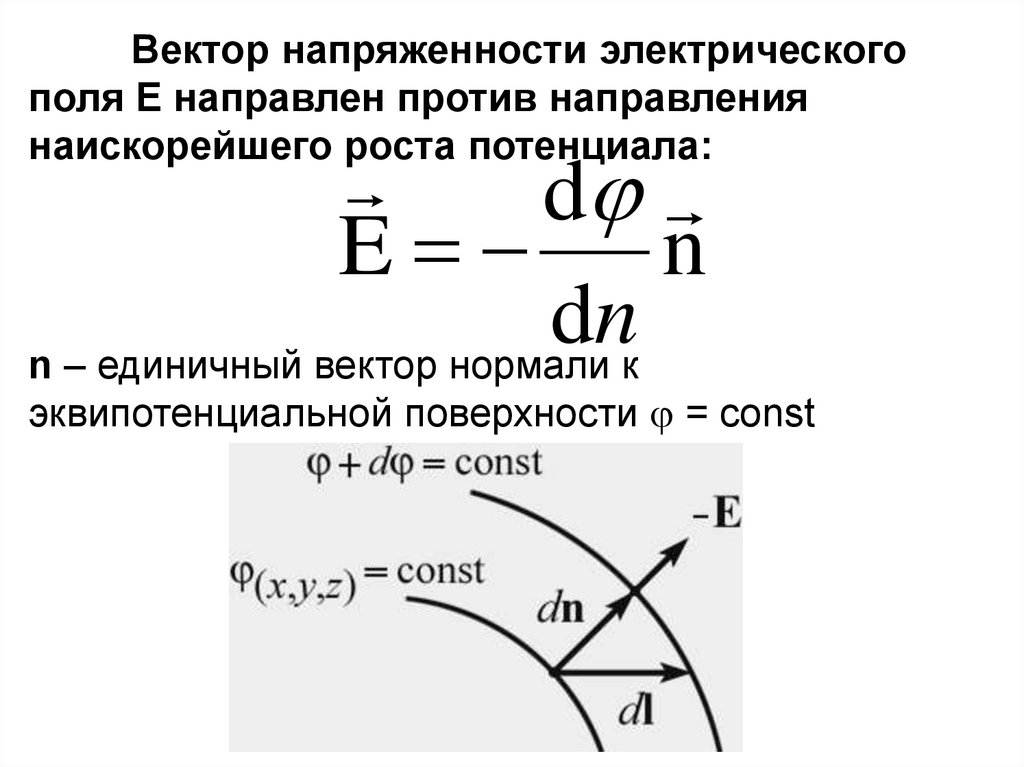
28.
Вектор напряженности электрическогополя Е направлен против направления
наискорейшего роста потенциала:
d
E
n
d
n
n – единичный вектор нормали к
эквипотенциальной поверхности = const
29. Безвихревой характер электростатического поля
E φ• Из условия
следует одно важное
соотношение, а именно,
величина, векторного
произведения [ , E] для стационарных электрических
полей всегда равна нулю. Действительно, по
определению, имеем
,
i
j
k
i
j
k
[ , E]
φ 0
x y z x y z
φ φ φ
x y z x y z
• поскольку определитель содержит две одинаковые
строки.
29
30.
• Величина [ , E]называется ротором иливихрем
• Мы получаем важнейшее уравнение
электростатики:
rotE 0
электростатическое поле –
безвихревое.
30
31.
• Согласно теореме Стокса, присутствуетследующая связь между контурным и
поверхностным интегралами:
(
E
,
d
l
)
rot
E
d
S
0
L
S
• где контур L ограничивающий поверхность S
ориентация которой определяется n
направлением вектора
положительной нормали
:
dS ndS
• Поэтому работа при перемещении заряда по
любому замкнутому пути в
электростатическом поле равна нулю.
31
32. Силовые линии и эквипотенциальные поверхности
Силовые линии и эквипотенциальные
поверхности
Направление силовой линии (линии
напряженности) в каждой
точке совпадает с направлением E .
• Отсюда следует, что напряженность равна разности
потенциалов U на единицу длины силовой линии.
• Именно вдоль силовой линии происходит максимальное
изменение потенциала. Поэтому всегда можно определить
между двумя точками, измеряя U между ними, причем
тем точнее, чем ближе точки.
• В однородном электрическом поле силовые линии – прямые.
Поэтому здесь определить E наиболее просто:
φ
U
E
l
32
33.
• Воображаемая поверхность, все точкикоторой имеют одинаковый потенциал,
называется эквипотенциальной
поверхностью.
• Уравнение этой поверхности
φ φ( x, y, z ) const.
33
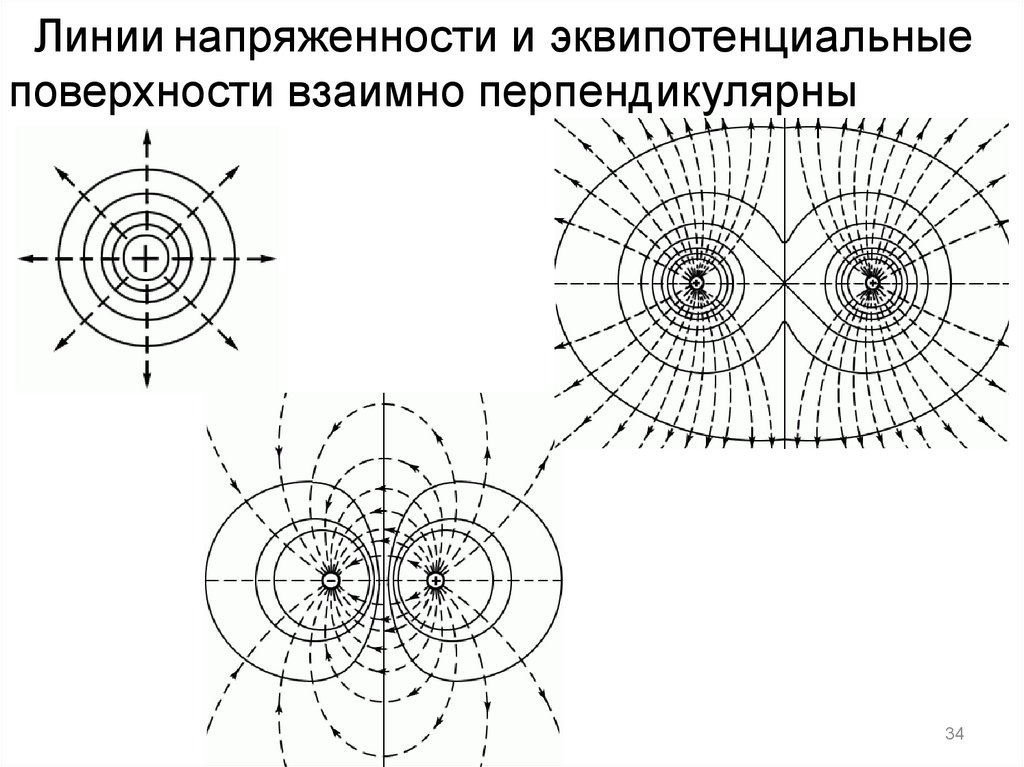
34.
Линии напряженности и эквипотенциальныеповерхности взаимно перпендикулярны
34
35.
E grad φ• Формула
выражает связь
потенциала с напряженностью и позволяет по
известным значениям φ найти напряженность
поля в каждой точке.
• Можно решить и обратную задачу, т.е. по
известным значениям E в каждой точке поля
найти разность потенциалов между двумя
произвольными точками поля.
φ1 φ 2 (E, d l ).
2
1
35
36.
φ1 φ 2 (E, d l ).2
1
• Интеграл можно брать по любой линии,
соединяющие точку 1 и точку 2, ибо работа сил
поля не зависит от пути.
• Для обхода по замкнутому контуру получим:
• т.е. пришли к известной нам теореме о φ1 φ 2
циркуляции вектора напряженности: циркуляция
вектора напряженности электростатического
поля вдоль любого замкнутого контура равна
нулю.
(E, d l ) 0,
Поле, обладающее этим свойством, называется потенциальным.
36
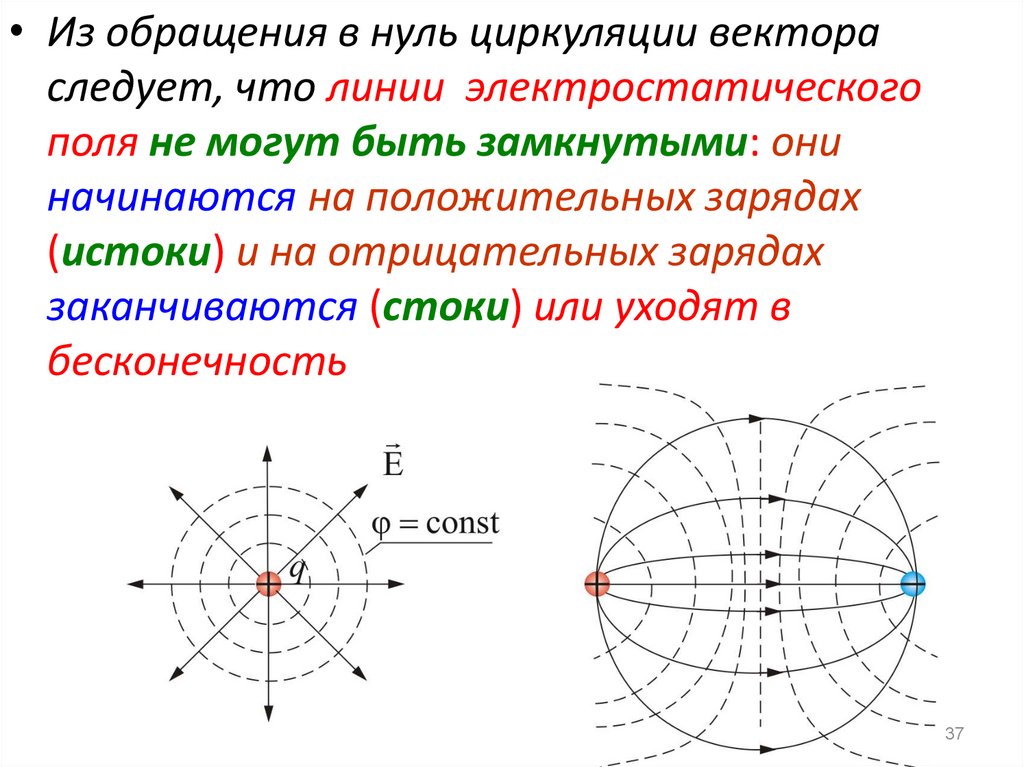
37.
• Из обращения в нуль циркуляции вектораследует, что линии электростатического
поля не могут быть замкнутыми: они
начинаются на положительных зарядах
(истоки) и на отрицательных зарядах
заканчиваются (стоки) или уходят в
бесконечность
37
38.
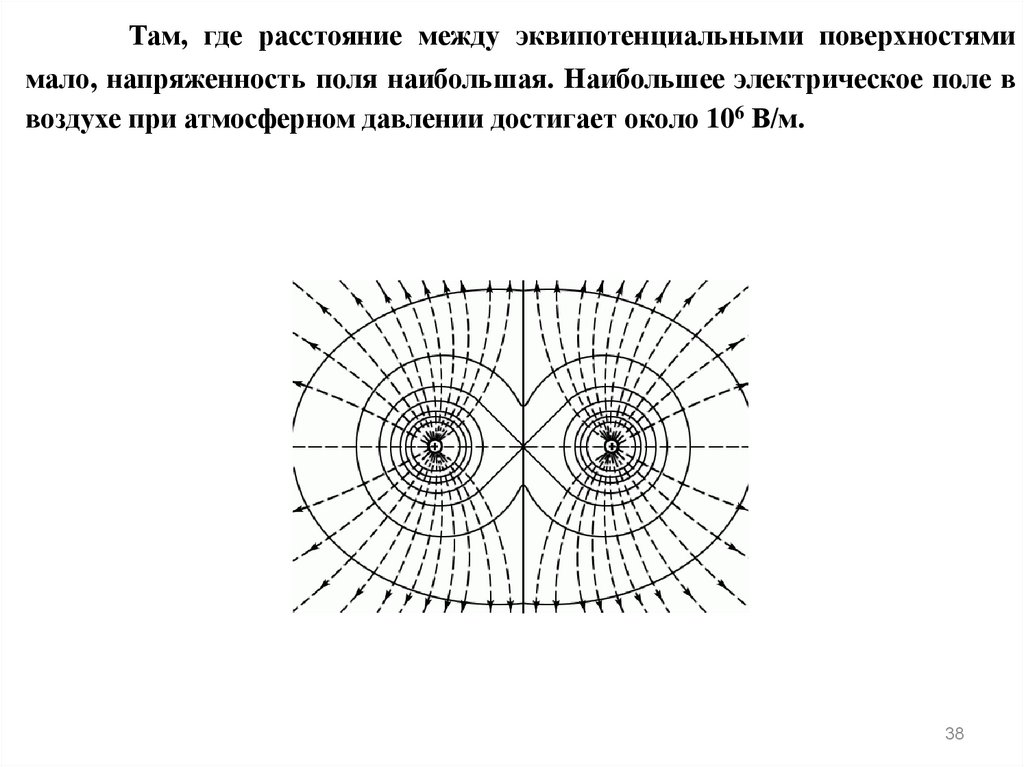
Там, где расстояние между эквипотенциальными поверхностямимало, напряженность поля наибольшая. Наибольшее электрическое поле в
воздухе при атмосферном давлении достигает около 106 В/м.
38
39. Расчет потенциалов простейших электростатических полей
• Рассмотрим несколько примеров вычисленияразности потенциалов между точками поля,
созданного некоторыми заряженными телами
39
40.
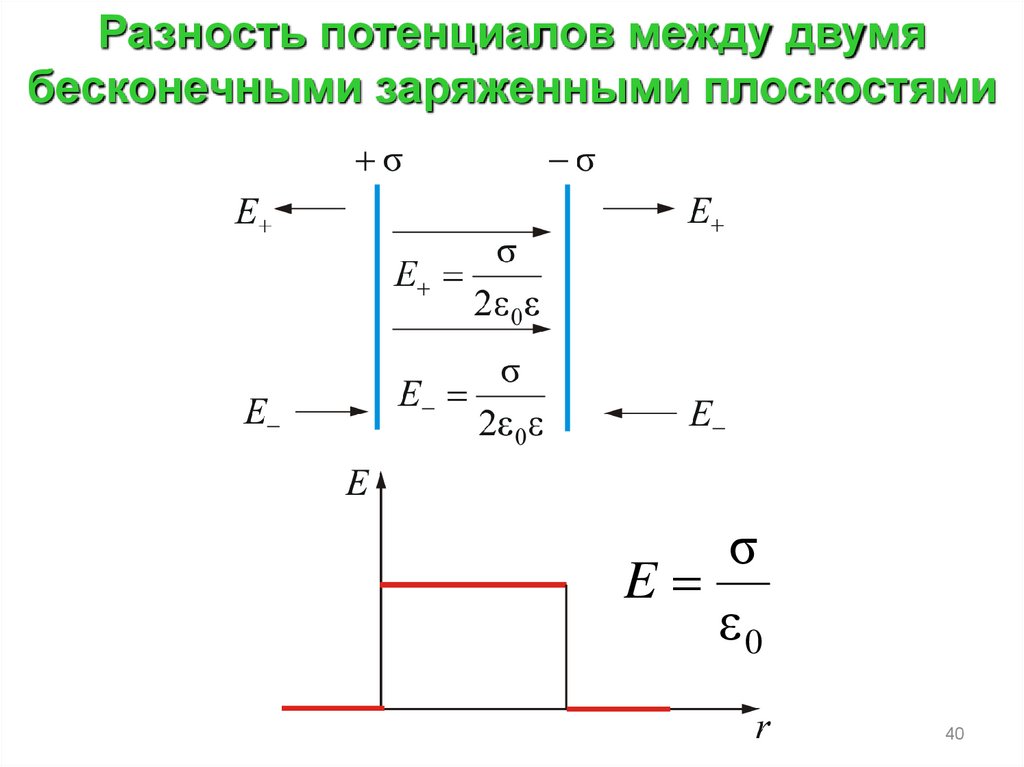
Разность потенциалов между двумябесконечными заряженными плоскостями
σ
E
ε0
40
41.
• Мы показали, что напряженность связана спотенциалом
dφ
E
, отсюда
d
l
dφ Edl
σ
• где E
– напряженность
ε0
электростатического поля между заряженными
плоскостями
• σ = q/S – поверхностная плотность заряда.
41
42.
Чтобы получить выражение для
потенциала между плоскостями,
проинтегрируем выражение dφ
2
Edl
x2
σ
dφ ε 0 dx;
1
x1
σ
φ 2 φ1 x2 x1
ε0
При x1 = 0 и x2 = d
σd
φ 2 φ1
ε0
42
43.
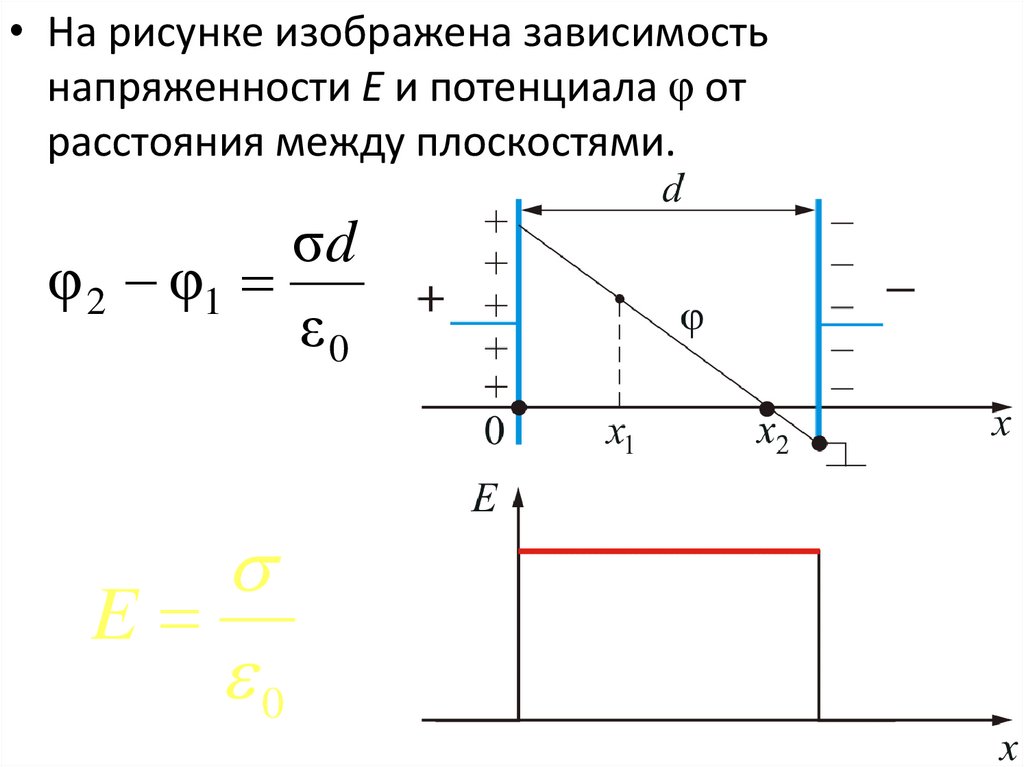
• На рисунке изображена зависимостьнапряженности E и потенциала φ от
расстояния между плоскостями.
σd
φ 2 φ1
ε0
E
0
43
44. Разность потенциалов между точками поля, образованного бесконечно длинной цилиндрической поверхностью
• С помощью теоремы Остроградского-Гауссамы показали, что
0
внутри
цилиндра,
т.к.
там
нет
зарядов
λ
q
E
или
на поверхности цилиндра
2
πε
R
2
πε
Rl
0
0
λ
q
или
вне цилиндра.
2 πε0 rl
2 πε0 r
44
45.
• Тогда,т.к.dφ Edr;
2
λ
dφ 2 πε 0
1
r2
r1
dr
r
• отсюда следует, что разность потенциалов в
произвольных точках 1 и 2 будет равна:
λ
r2
q
r2
ln
ln
• φ 2 φ1
2πε0 r1
2πε0l r1
1
λ
ln
const
внутри
и
на
поверхност
и
2πε
R
0
φ
λ ln r вне цилиндра.
2πε0 R
45
46.
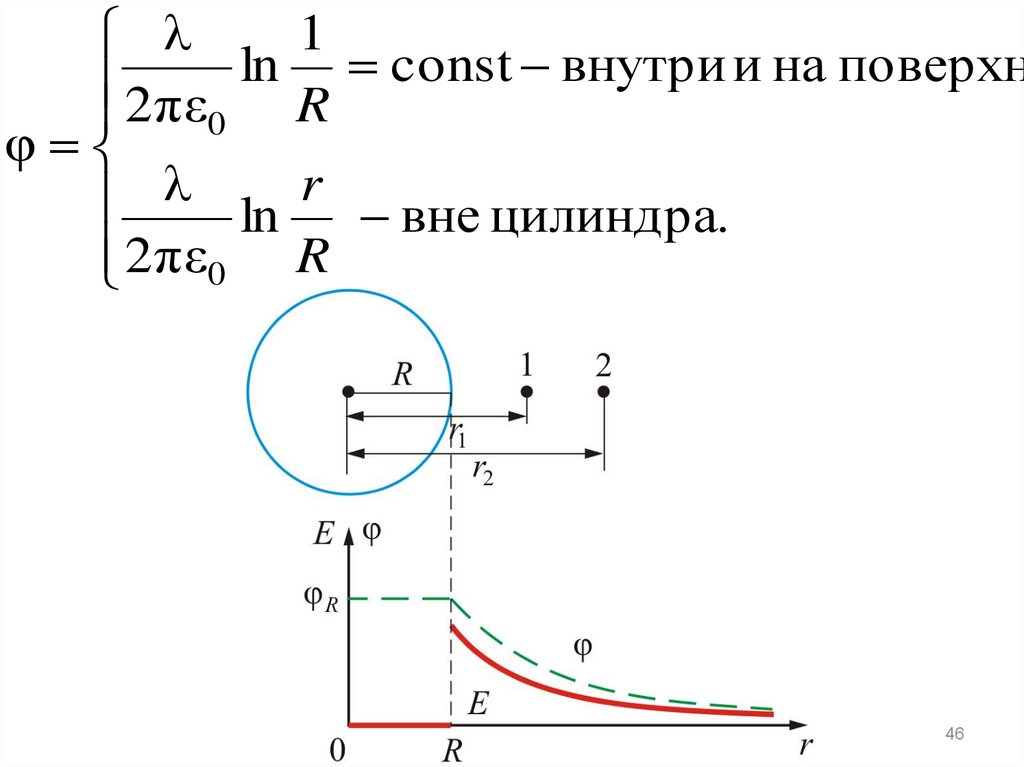
λln
2πε
0
φ
λ ln
2πε0
1
const внутри и на поверхн
R
r
вне цилиндра.
R
46
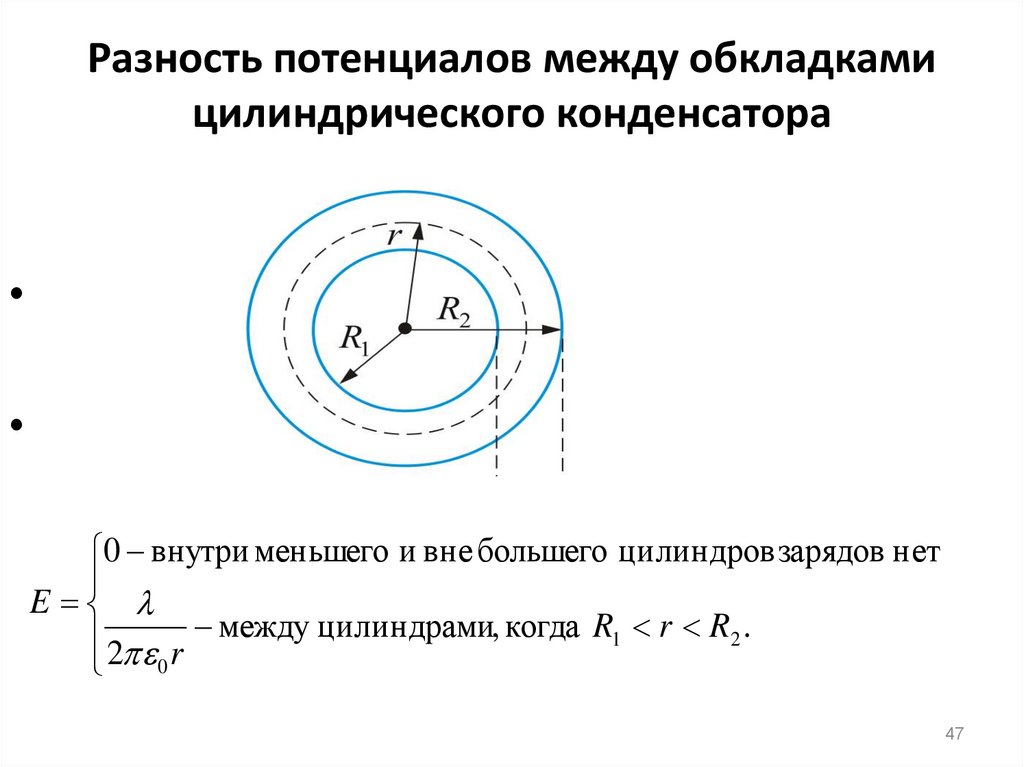
47. Разность потенциалов между обкладками цилиндрического конденсатора
0 внутри меньшего и вне большего цилиндров зарядов нет
E
2 r между цилиндрами, когда R1 r R2 .
0
47
48.
• Т.к.dφ Edr
, то
λ
r2
φ 2 φ1
ln
2πε0 r1
R2
λ
2 πε ln R const внутри меньшего цилиндра (r R1 )
0
1
r
λ
φ
ln между цилиндрами ( R1 r R2 )
2 πε0 R1
0 вне цилиндров.
48
49.
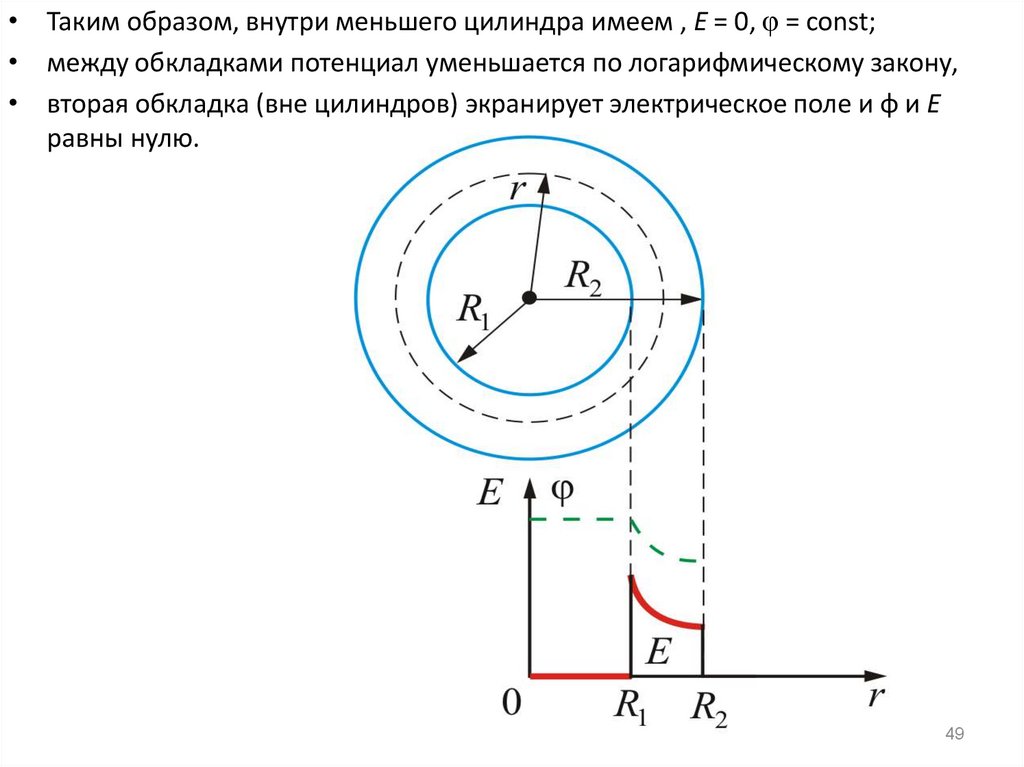
• Таким образом, внутри меньшего цилиндра имеем , Е = 0, φ = const;• между обкладками потенциал уменьшается по логарифмическому закону,
• вторая обкладка (вне цилиндров) экранирует электрическое поле и φ и Е
равны нулю.
49
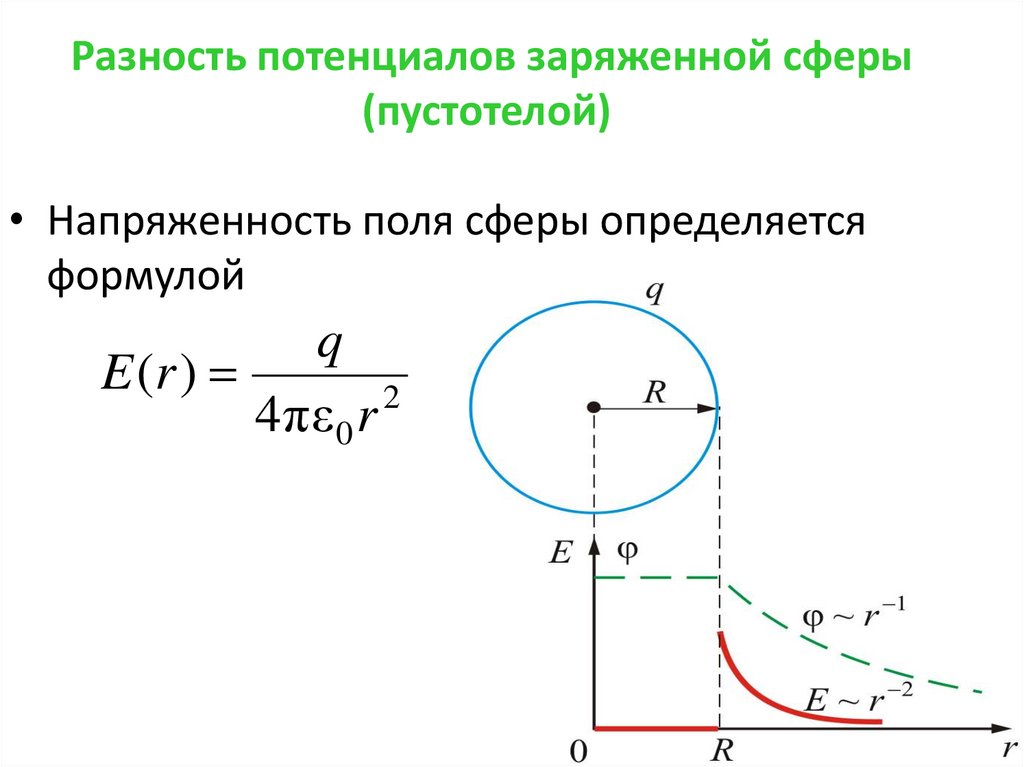
50. Разность потенциалов заряженной сферы (пустотелой)
• Напряженность поля сферы определяетсяформулой
q
E (r )
2
4 πε 0 r
50
51.
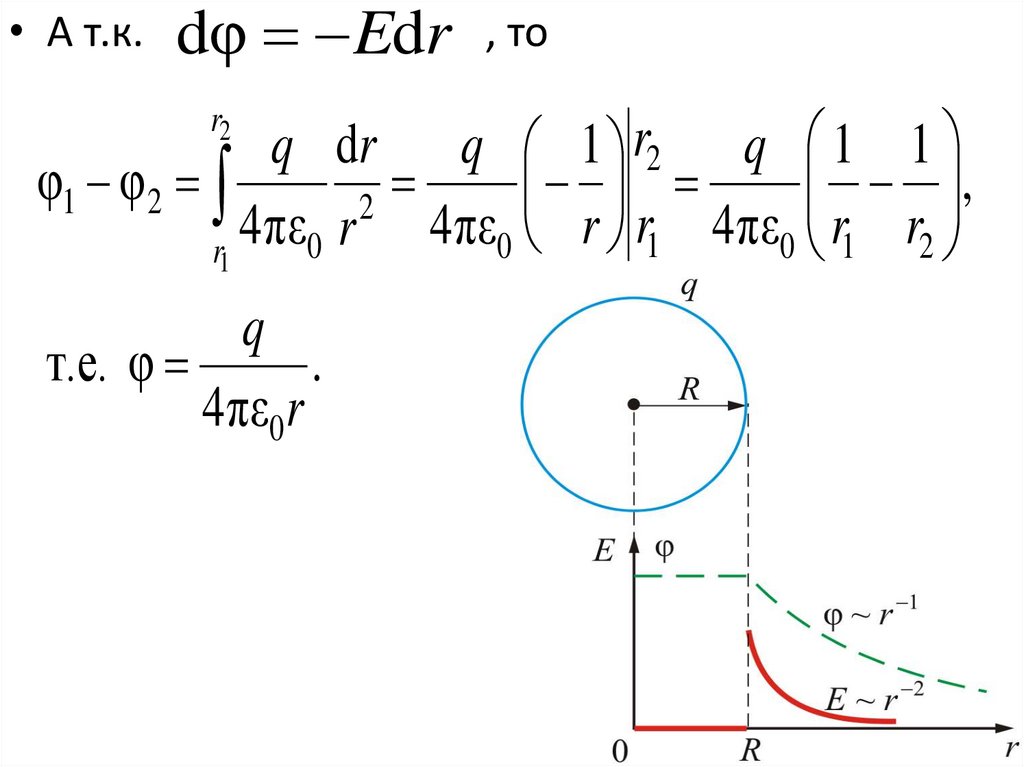
• А т.к.dφ Edr
, то
q dr q 1 r2 q 1 1
φ1 φ2
,
2
r
4
πε
4
πε
r
4
πε
r
r
r
1
0
0
0
1
2
r1
r2
q
т.е. φ
.
4πε0r
51
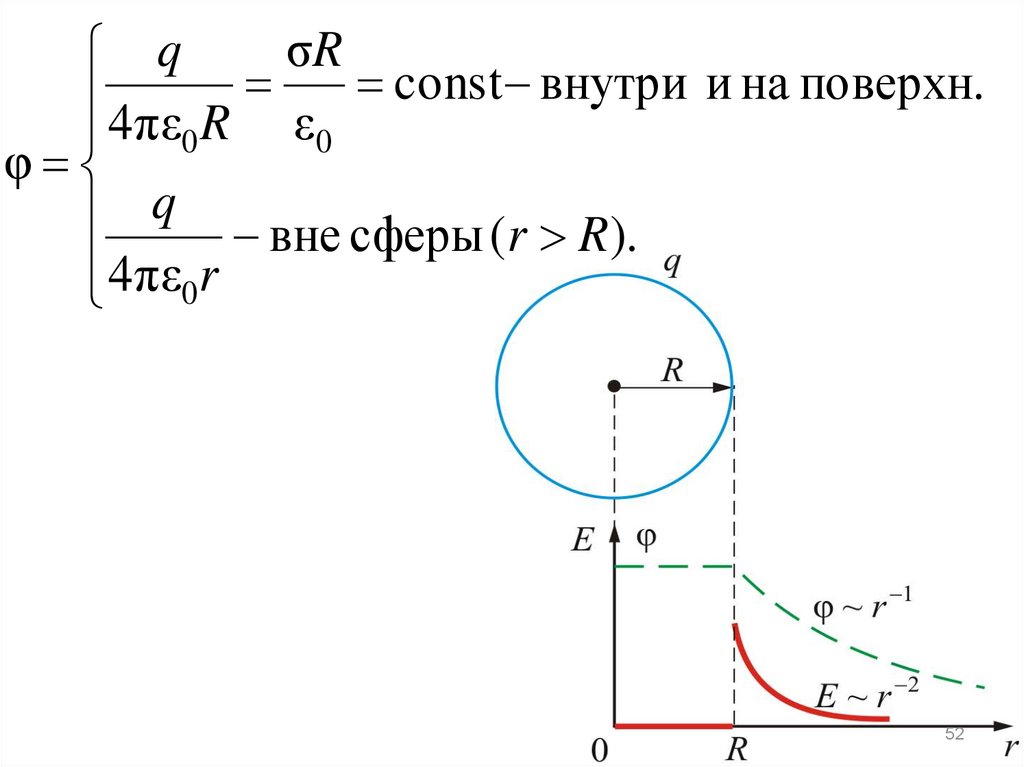
52.
σRq
const
внутри
и
на
поверхн.
4πε R ε
0
0
φ
q вне сферы (r R).
4πε0r
52
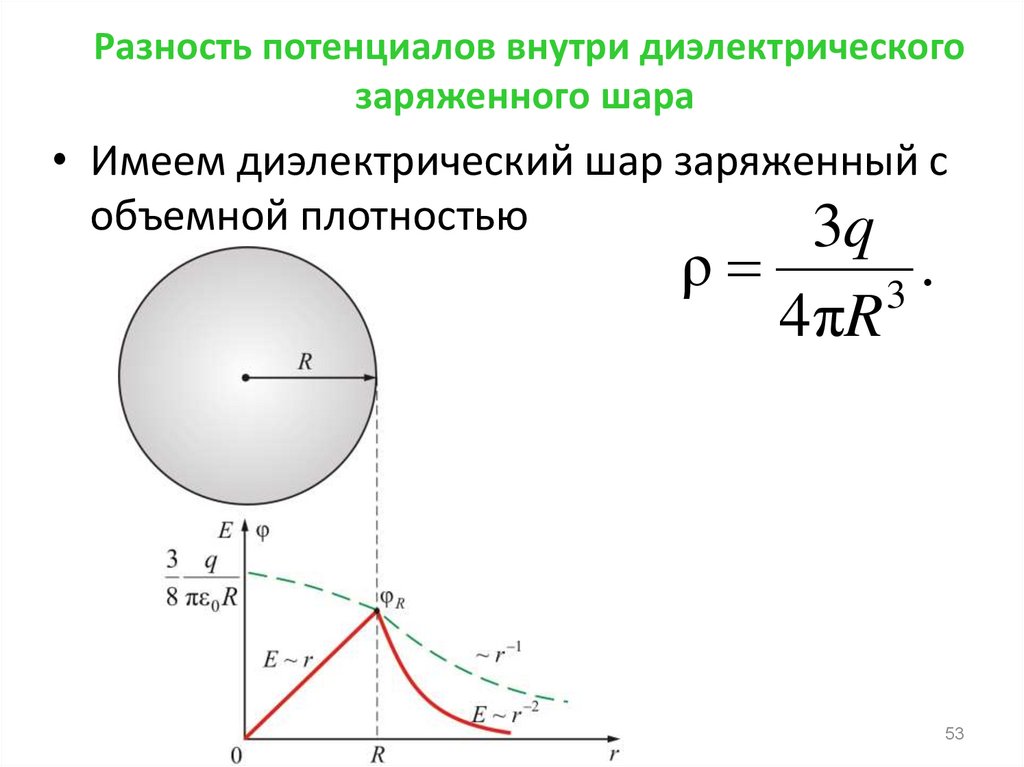
53. Разность потенциалов внутри диэлектрического заряженного шара
• Имеем диэлектрический шар заряженный собъемной плотностью
3q
ρ
4 πR
.
3
53
54.
• Напряженность поля шара, вычисленная спомощью теоремы Остроградского-Гаусса:
qr
ρr
внутри шара (r R )
3
3
ε
4
πε
R
0
0
q
E
на
поверхност
и
шара
(
r
R
)
2
4 πε0 R
q
вне шара (r R ).
2
4 πε0 r
54
55.
• Отсюда найдем разность потенциалов шара:2
2
ρ
ρ 2
2
φ 2 φ1 Edr
rdr
r2 r1
3ε 0 1
6ε 0
1
или
φ1 φ 2
2
r1 )
.
3
4πε0 2R
2
q(r2
55
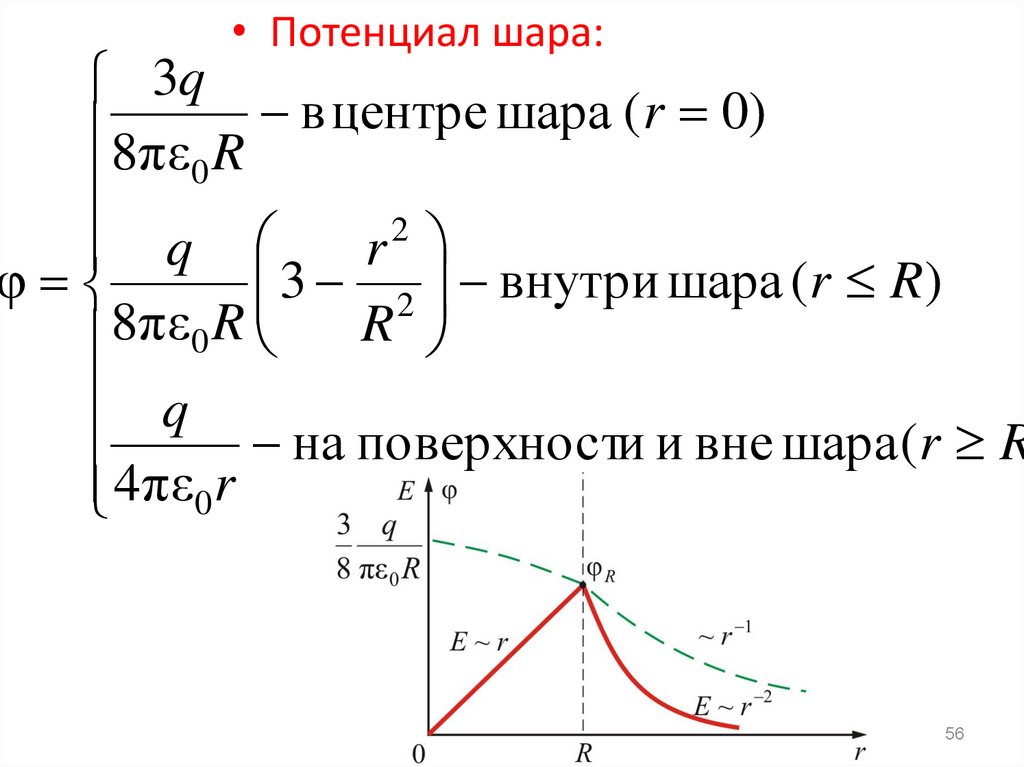
56.
• Потенциал шара:3q
в
центре
шара
(
r
0
)
8πε R
0
2
q
r
3 2 внутри шара (r R)
φ
8
πε
R
R
0
q
на поверхности и вне шара (r R
4 πε0 r
56
57.
• Из полученных соотношений можносделать следующие выводы:
• С помощью теоремы Гаусса сравнительно
просто можно рассчитать Е и φ от
различных заряженных поверхностей.
• Напряженность поля в вакууме
изменяется скачком при переходе через
заряженную поверхность.
• Потенциал поля – всегда непрерывная
функция координат.
57






































 physics
physics








