Потенциал и работа электростатического поля. Связь напряженности с потенциалом

1.

Тема 3. ПОТЕНЦИАЛ И РАБОТА
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ.
СВЯЗЬ НАПРЯЖЕННОСТИ С ПОТЕНЦИАЛОМ
E
3.1. Теорема о циркуляции вектора
3.2. Работа сил электростатического поля.
Потенциальная энергия
3.3. Потенциал. Разность потенциалов
3.4. Связь между напряженностью и
потенциалом
3.5. Силовые линии и эквипотенциальные
поверхности
3.6. Расчет потенциалов простейших
электростатических полей
1

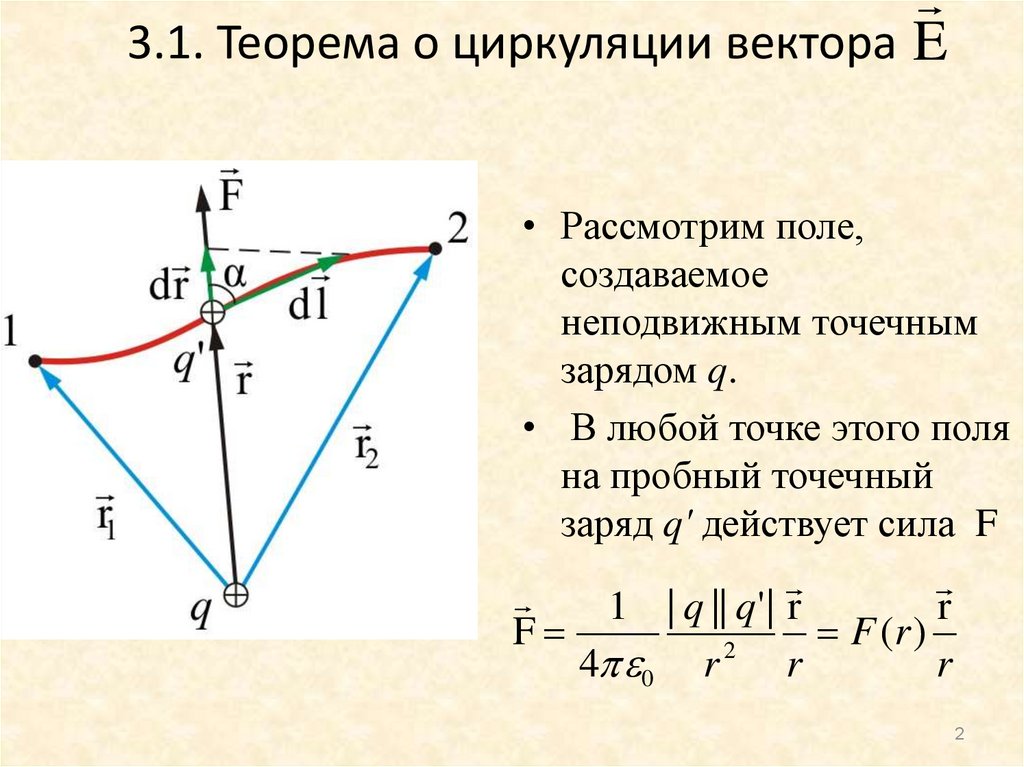
2. 3.1. Теорема о циркуляции вектора

E
• Рассмотрим поле,
создаваемое
неподвижным точечным
зарядом q.
• В любой точке этого поля
на пробный точечный
заряд q' действует сила F
1 | q || q ' | r
r
F
F (r )
2
4 0 r
r
r
2

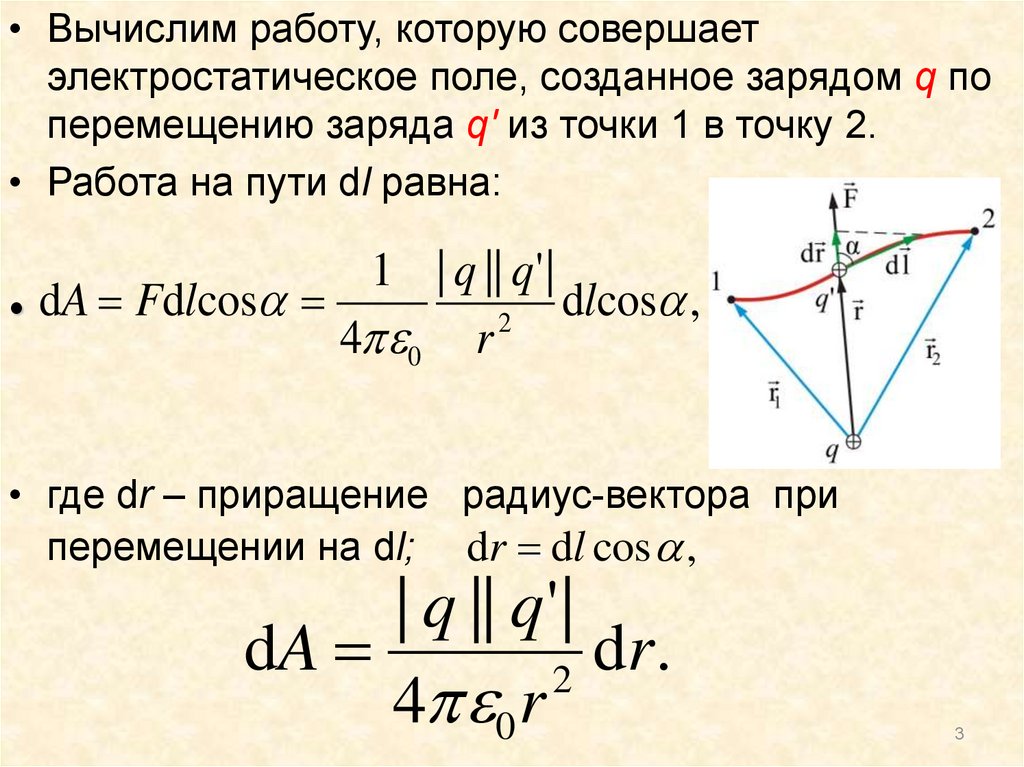
3.

• Вычислим работу, которую совершает
электростатическое поле, созданное зарядом q по
перемещению заряда q' из точки 1 в точку 2.
• Работа на пути dl равна:
1 | q || q' |
dlcos ,
• dA Fdlcos
2
4 0 r
• где dr – приращение радиус-вектора при
перемещении на dl; dr dl cos ,
| q || q ' |
dA
d
r
.
2
4 0 r
3

4.

• Полная работа при перемещении из точки 1 в
точку 2 равна интегралу:
| q || q'| dr | q || q'| 1 r2 | q || q'| 1 1
A12
.
2
4 0 r1 r
4 0 r r1 4 0 r1 r2
r2
• Работа электростатических сил не зависит от
формы пути, а только лишь от координат
начальной и конечной точек перемещения.
Следовательно, силы поля консервативны, а
само поле – потенциально.
4

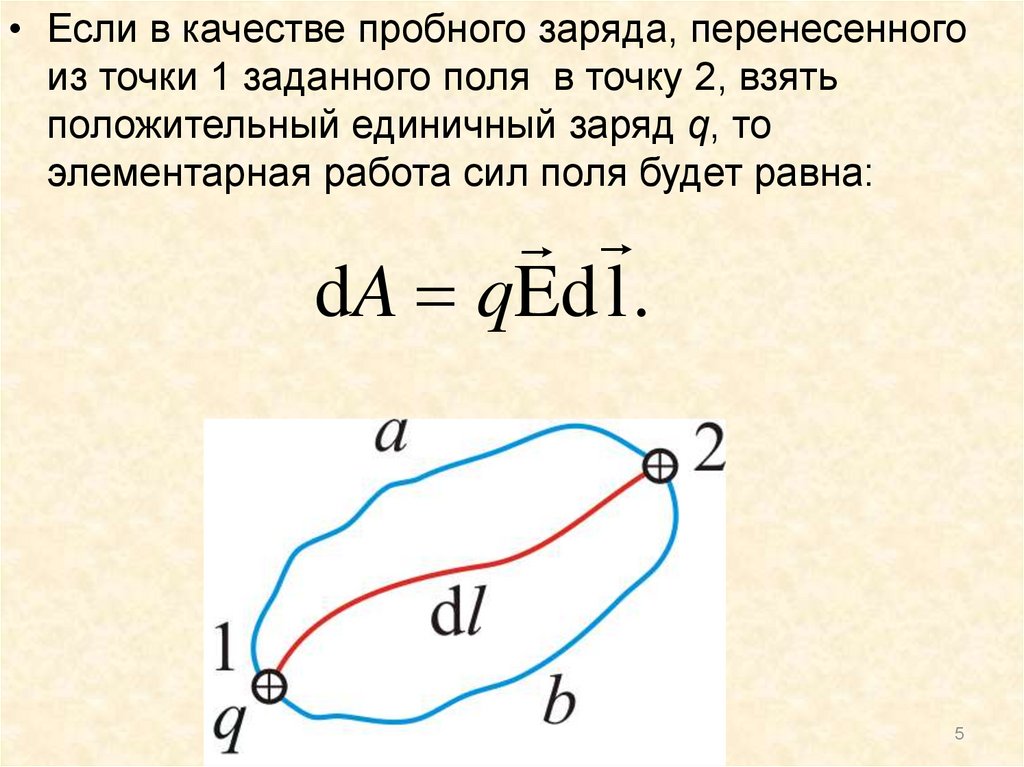
5.

• Если в качестве пробного заряда, перенесенного
из точки 1 заданного поля в точку 2, взять
положительный единичный заряд q, то
элементарная работа сил поля будет равна:
dA qEd l .
5

6.

A q Ed l .
2
• Тогда вся работа равна:
1
• Такой интеграл по замкнутому
контуру называется
циркуляцией вектора E
• Из независимости линейного интеграла от пути
между двумя точками следует, что по
произвольному замкнутому пути:
E
d
l
0
.
• Это утверждение и называют теоремой о
циркуляции.
• Линии электростатического поля не могут быть
замкнутыми
6

7. 3.2. Работа сил электростатического поля. Потенциальная энергия

• Электростатическое поле потенциально, т.е.
обладает потенциальной энергией.
• Работу сил электростатического поля:
A12 W1 W2 .
Это выражение для работы можно переписать в
виде:
qq'
qq'
A12
4 0 r1
4 0 r2
.
• Потенциальная энергия заряда q' в поле заряда q:
1 qq'
W
const.
4 0 r
7

8. 3.3. Потенциал. Разность потенциалов

• Разные пробные заряды q',q'',… будут обладать в
одной и той же точке поля разными энергиями W',
W'' и так далее.
• Однако отношение W / q'пр. будет для всех
зарядов одним и тем же.
• Поэтому можно вести скалярную величину,
являющуюся энергетической характеристикой
собственно поля – потенциал:
W
.
q'
8

9.

• потенциал численно равен потенциальной
энергии, которой обладает в данной точке поля
единичный положительный заряд.
W
.
q'
• потенциал точечного заряда
1 q
.
4 0 r
• физический смысл имеет разность потенциалов,
поэтому договорились считать, что потенциал
точки, удаленной в бесконечность, равен нулю.
9

10.

• Другое определение потенциала:
A
q
или
A q
• потенциал численно равен работе, которую
совершают силы поля над единичным
положительным зарядом при удалении его из
данной точки в бесконечность
10

11.

• Если поле создается системой зарядов, то:
qk q '
W
.
4 0 k rk
1
qk
• Для потенциала k или
4 0 k rk
k
1
• т.е. потенциал поля, создаваемый системой зарядов,
равен алгебраической сумме потенциалов,
создаваемых каждым из зарядов в отдельности.
11

12.

• Работа сил электростатического поля через разность
потенциалов между начальной и конечной точками:
A12 W1 W2 1q 2q q 1 2 .
• Работа над зарядом q равна произведению заряда на
убыль потенциала:
A q 1 2 qU ,
где U – напряжение.
A qU
12

13.

• за единицу φ принимают потенциал в такой точке
поля, для перемещения в которую из
бесконечности единичного положительного заряда
необходимо совершить работу равную единице.
• В СИ единица потенциала
1 В 1 Дж/1 Кл
• Электрон - вольт (эВ) – это работа, совершенная
силами поля над зарядом, равным заряду
электрона при прохождении им разности
потенциалов 1 В, то есть:
1 эВ 1,6 10
19
Кл В 1,6 10
19
Дж.
13

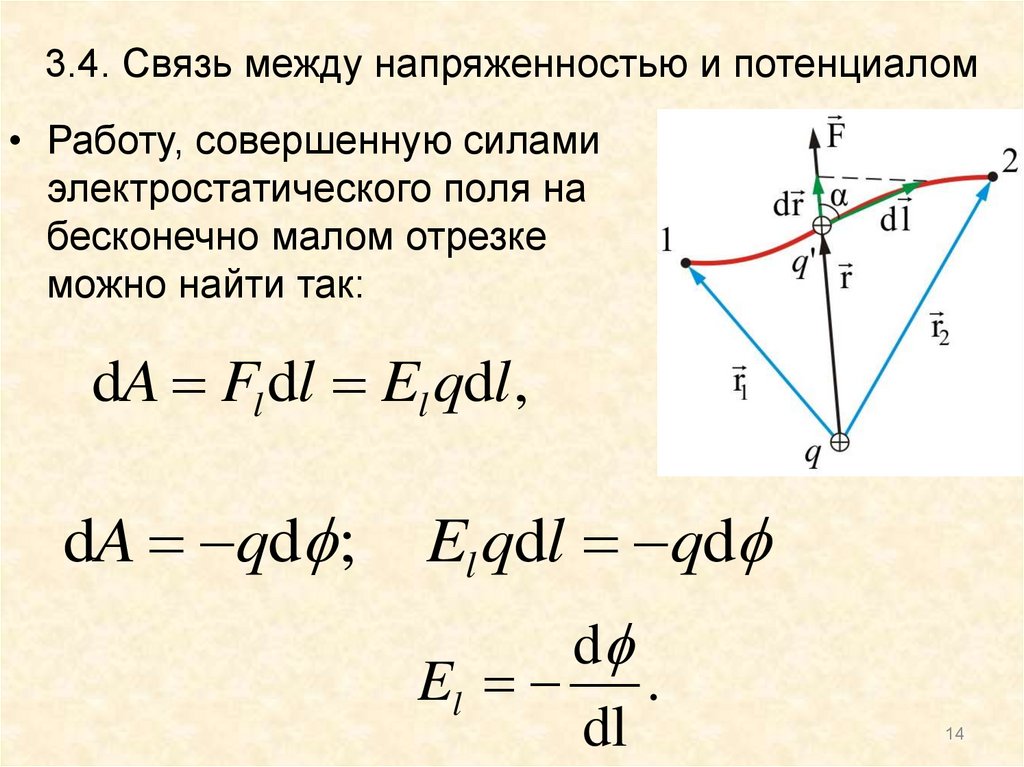
14. 3.4. Связь между напряженностью и потенциалом

• Работу, совершенную силами
электростатического поля на
бесконечно малом отрезке
можно найти так:
dA Fl dl El qdl ,
dA qd ;
El qdl qd
d
El .
dl
14

15.

• Тогда
E i
j
k,
x
y
z
• По определению градиента сумма первых
производных от какой-либо функции по
координатам есть градиент этой функции
grad
– вектор, показывающий направление
наибыстрейшего увеличения функции.
grad i
j k,
x
y
z
E grad
15

16.

E
•Где (набла) означает символический вектор,
называемый оператором Гамильтона
Знак минус говорит о том, что вектор направлен в
сторону уменьшения потенциала электрического
поля.
16

17.

E
•Из условия
следует одно важное
соотношение, а именно,
величина, векторного
произведения [ , E] для стационарных
электрических полей всегда равна нулю.
•Величина [ , E] называется ротором или вихрем
•Уравнение электростатики:
rotE 0
•Таким образом кулоновское электростатическое
поле – безвихревое.
17

18. 3.5. Силовые линии и эквипотенциальные поверхности

• Напряженность равна разности потенциалов U на
единицу длины силовой линии.
• В однородном электрическом поле силовые линии
– прямые. Поэтому здесь определить E
наиболее просто:
U
E
l
18

19.

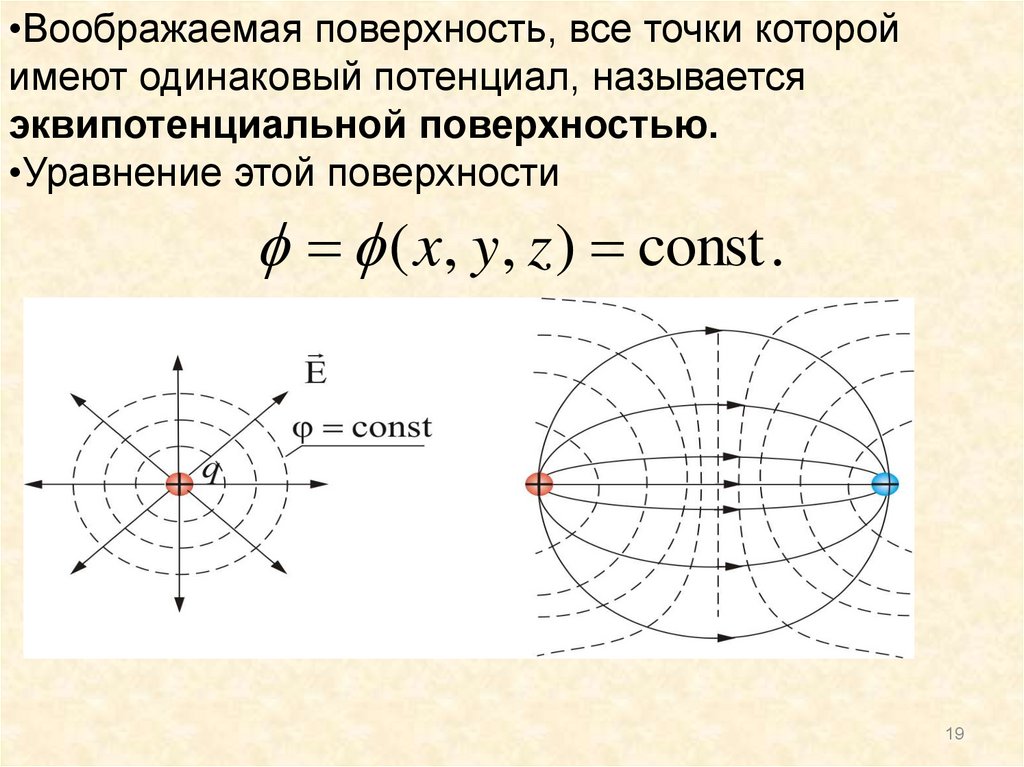
•Воображаемая поверхность, все точки которой
имеют одинаковый потенциал, называется
эквипотенциальной поверхностью.
•Уравнение этой поверхности
( x, y, z ) const .
19

20.

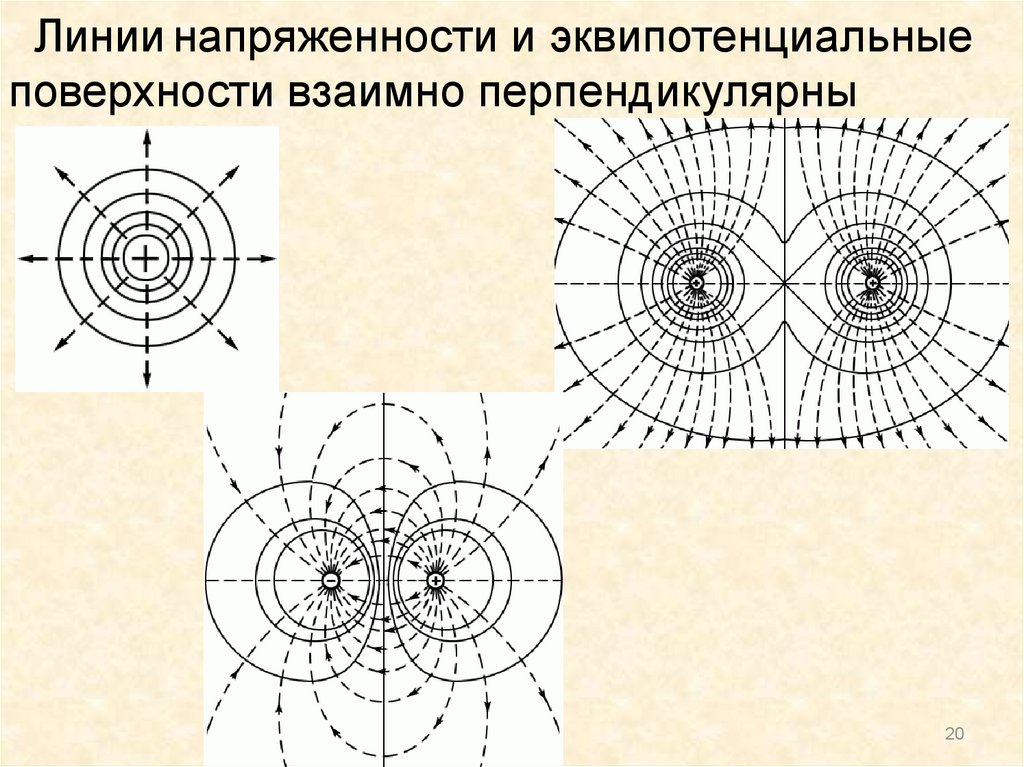
Линии напряженности и эквипотенциальные
поверхности взаимно перпендикулярны
20

21.

• Можно по известным значениям φ найти
напряженность поля в каждой точке.
E grad
• или по известным значениям E в каждой точке
поля найти разность потенциалов между двумя
2
произвольными точками поля.
1 2 (E, d l ).
1
• Для обхода по замкнутому контуру
получим:
1
2
(E, d l ) 0,
•циркуляция вектора напряженности
электростатического поля вдоль любого замкнутого
контура равна нулю.
21

22.

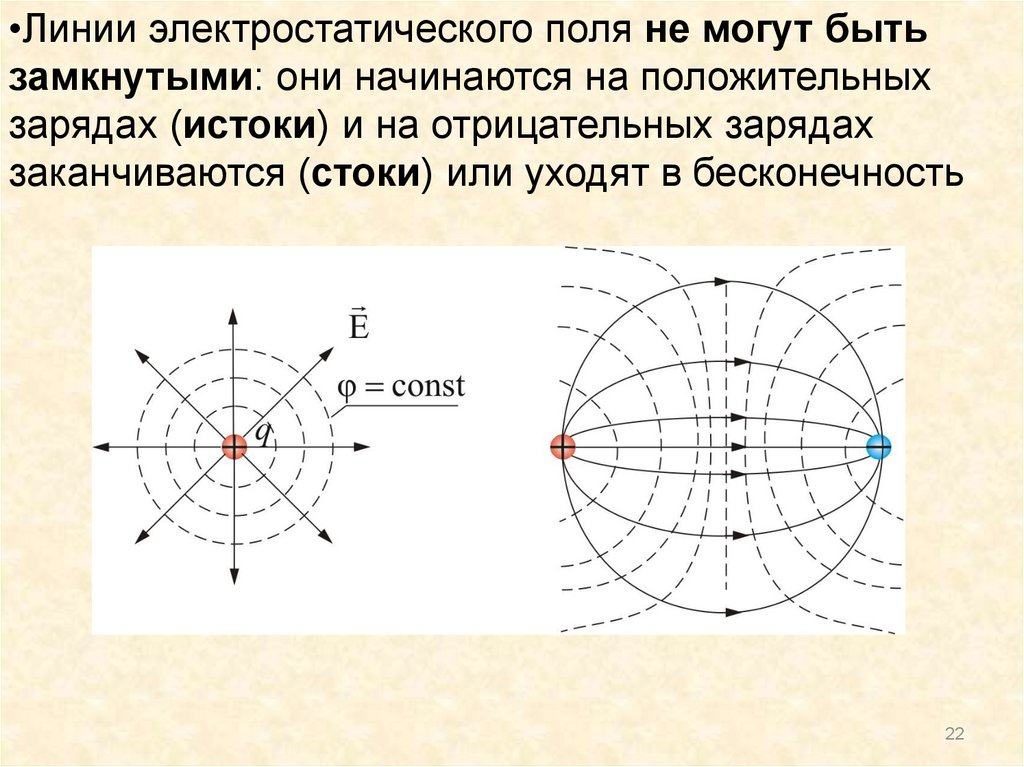
•Линии электростатического поля не могут быть
замкнутыми: они начинаются на положительных
зарядах (истоки) и на отрицательных зарядах
заканчиваются (стоки) или уходят в бесконечность
22

23. 3.7. Расчет потенциалов простейших электростатических полей

3.7.1. Разность потенциалов между двумя
бесконечными заряженными плоскостями
d
E
,
dl
E
| |
d Edl
0
| |
2
x2
d dx;
0
1
2 1
| |
0
x1
x2 x1
23

24.

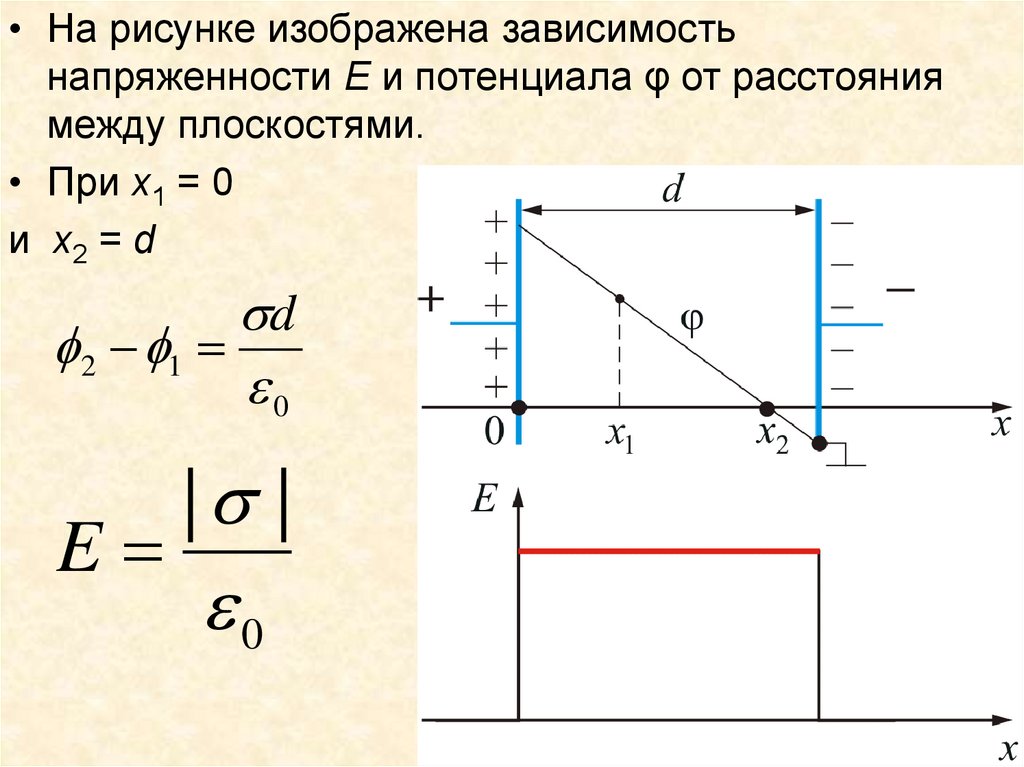
• На рисунке изображена зависимость
напряженности E и потенциала φ от расстояния
между плоскостями.
• При x1 = 0
и x2 = d
d
2 1
0
E
| |
0
24

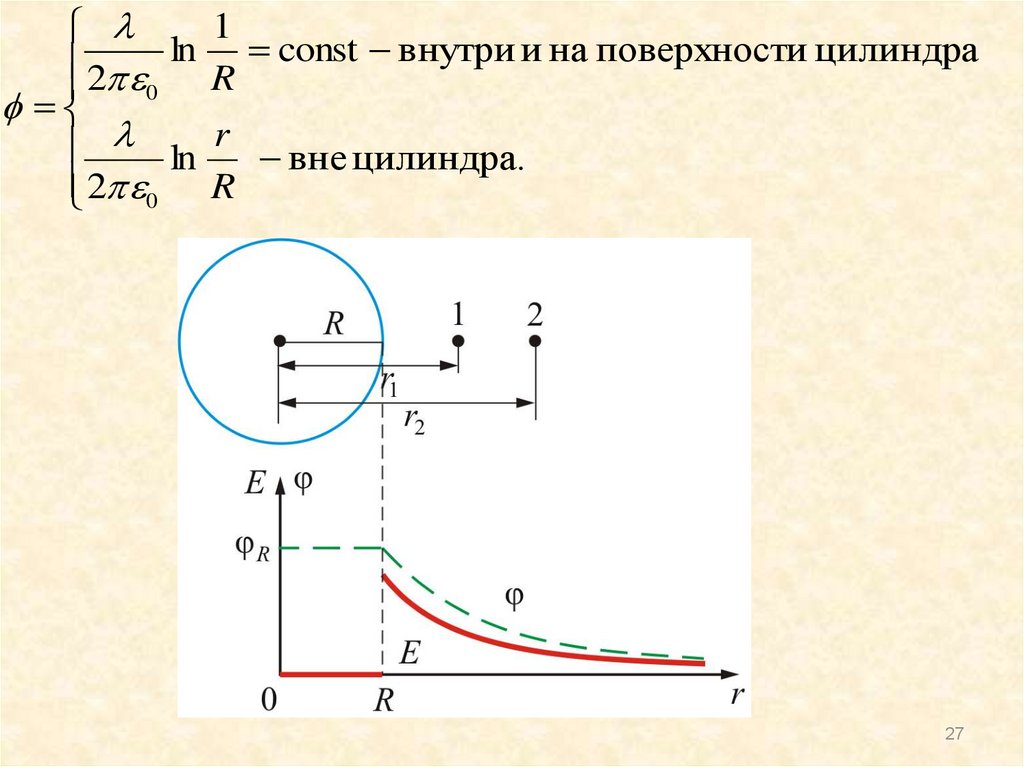
25. 3.7.2. Разность потенциалов между точками поля, образованного бесконечно длинной цилиндрической поверхностью

• С помощью теоремы Остроградского-Гаусса мы
показали, что
0
внутри
цилиндра,
так
как
внутри
нет
зарядов
q
E
или
на поверхности цилиндра
2 0 Rl
2 0 R
q
или
вне цилиндра.
2 0 rl
2 0 r
25

26.

• Тогда, т.к.
d Edr;
dr
1 d 2 0 r r
2
r2
1
• отсюда следует, что разность потенциалов в
произвольных точках 1 и 2 будет равна:
r2
q
r2
2 1
ln
ln
2 0 r1
2 0l r1
• ln 1 const на поверхности и внутри цилиндра
2 0 R
ln r вне цилиндра.
2 0 R
26

27.

1
2 ln R const внутри и на поверхности цилиндра
0
ln r вне цилиндра.
2 0 R
27

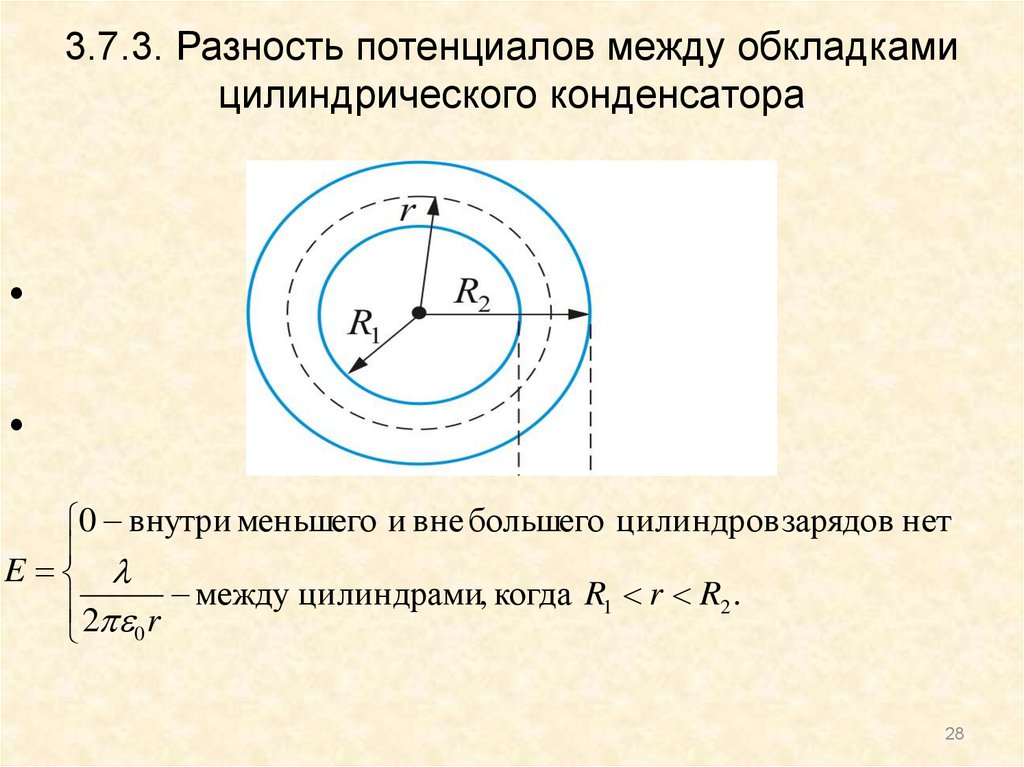
28. 3.7.3. Разность потенциалов между обкладками цилиндрического конденсатора

0 внутри меньшего и вне большего цилиндров зарядов нет
E
2 r между цилиндрами, когда R1 r R2 .
0
28

29.

• Т.к.
d Edr
, то
r2
2 1
ln
2 0 r1
R2
2 ln R const внутри меньшего цилиндра (r R1 )
0
1
r
ln
между цилиндрами ( R1 r R2 )
2 0 R1
0 вне цилиндров.
29

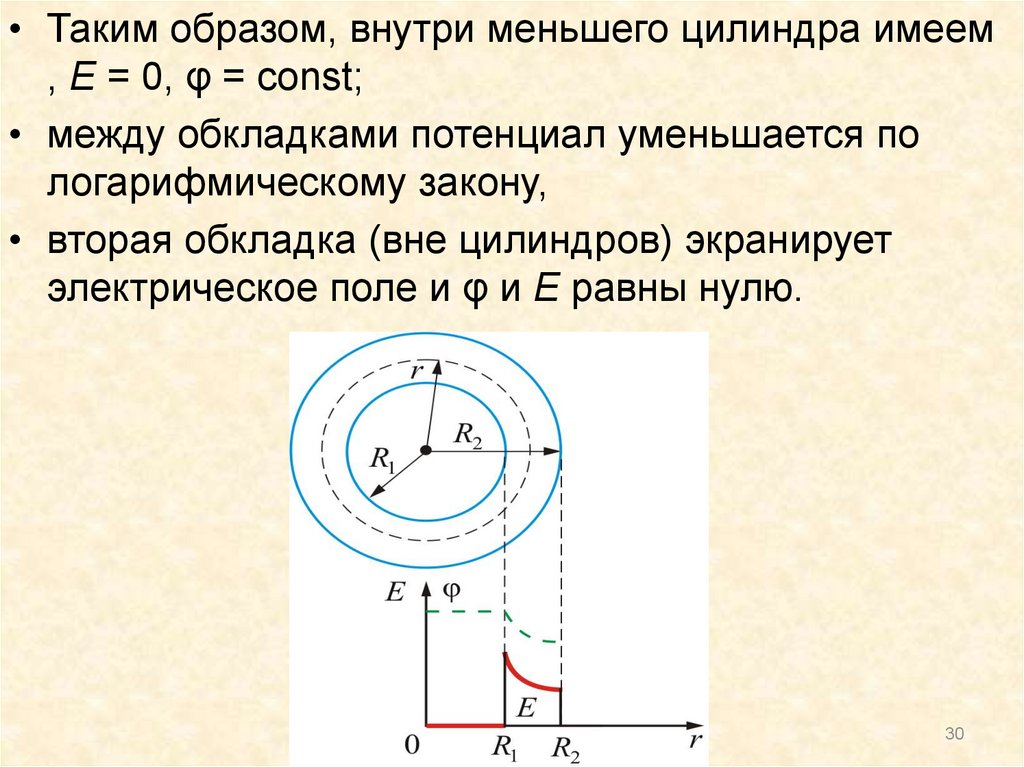
30.

• Таким образом, внутри меньшего цилиндра имеем
, Е = 0, φ = const;
• между обкладками потенциал уменьшается по
логарифмическому закону,
• вторая обкладка (вне цилиндров) экранирует
электрическое поле и φ и Е равны нулю.
30

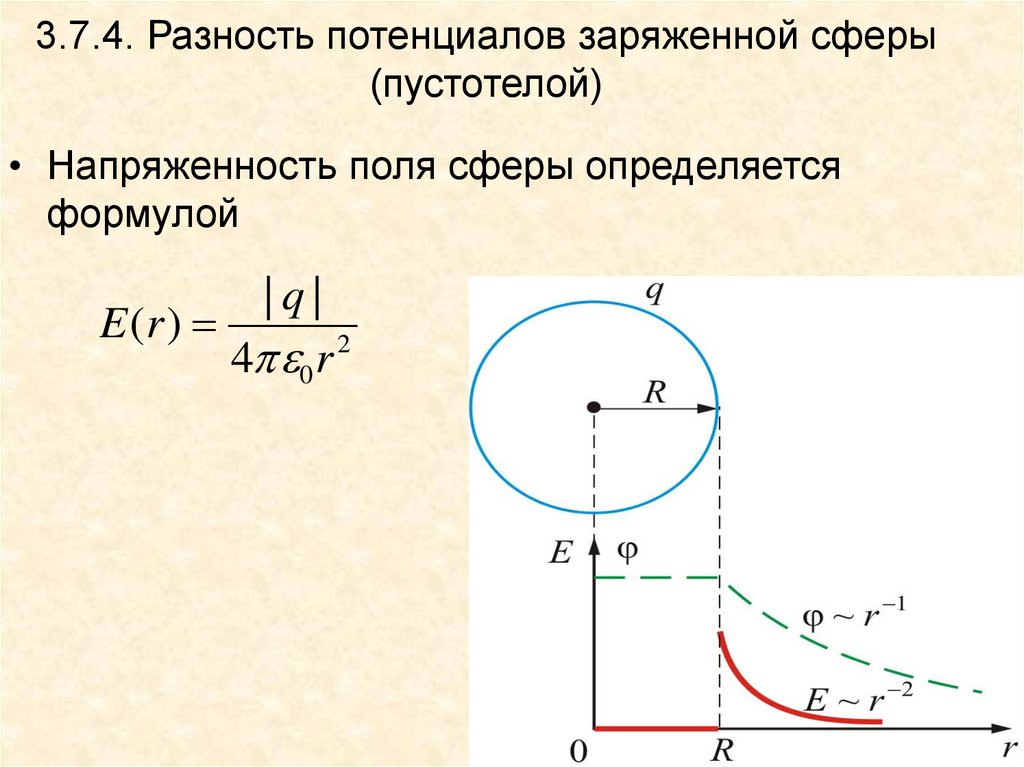
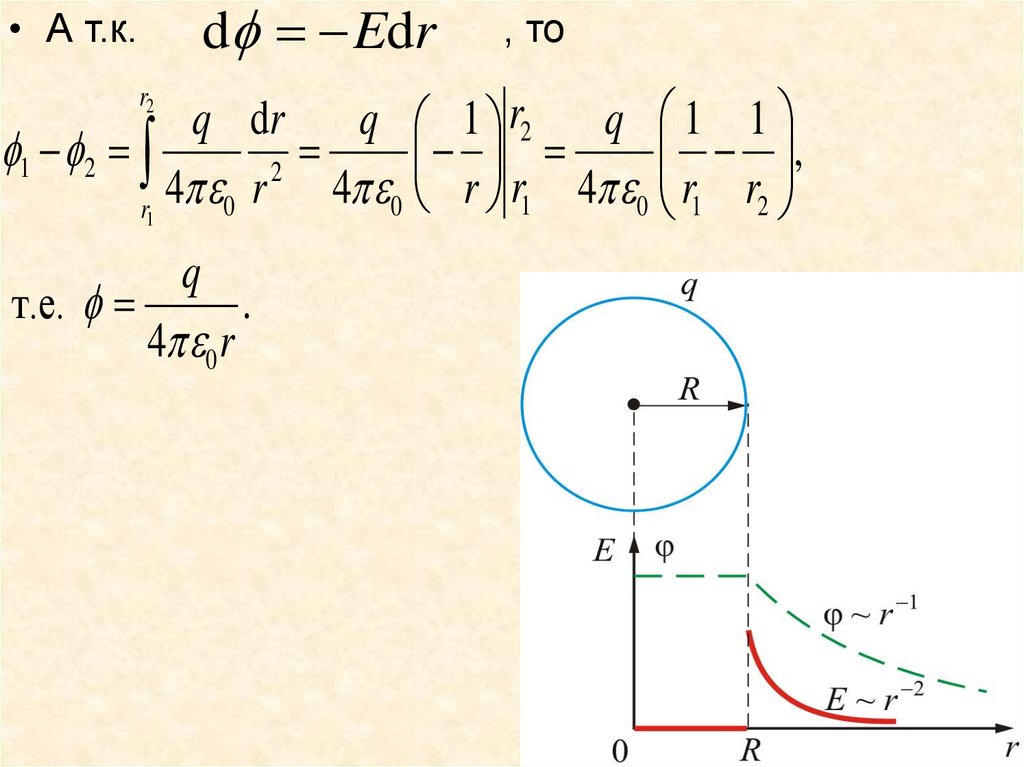
31. 3.7.4. Разность потенциалов заряженной сферы (пустотелой)

• Напряженность поля сферы определяется
формулой
|q|
E (r )
2
4 0 r
31

32.

d Edr
• А т.к.
, то
q dr
q 1 r2 q 1 1
1 2
,
2
4 0 r 4 0 r r1 4 0 r1 r2
r1
r2
q
т.е.
.
4 0 r
32

33.

R
q
4 R const внутри и на поверхности
0
0
q вне сферы (r R).
4 0 r
33

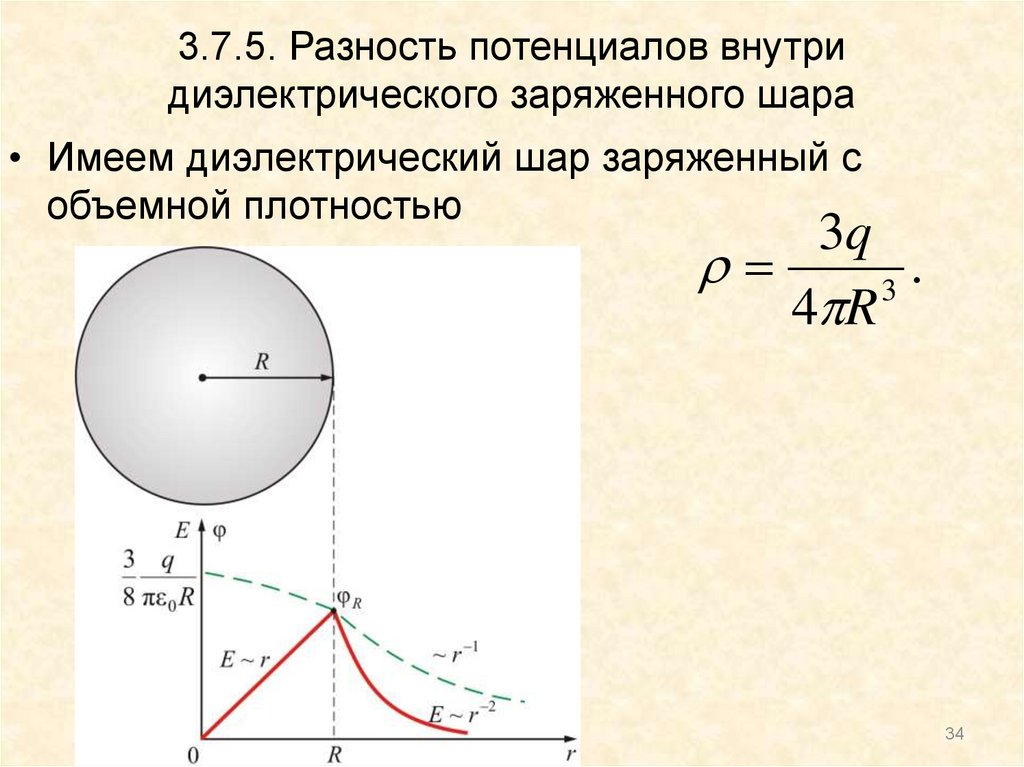
34. 3.7.5. Разность потенциалов внутри диэлектрического заряженного шара

• Имеем диэлектрический шар заряженный с
объемной плотностью
3q
.
3
4 R
34

35.

• Напряженность поля шара, вычисленная с
помощью теоремы Остроградского-Гаусса:
qr
r
внутри шара (r R)
3
3 0
4 0 R
q
E
на поверхности шара (r R)
2
4 0 R
q
вне шара (r R).
2
4 0 r
35

36.

• Отсюда найдем разность потенциалов шара:
2 2
2 1 Edr
rdr
r2 r1
3 0 1
6 0
1
2
2
или
q(r r )
1 2
.
4 0 2 R
2
2
2
1
3
36

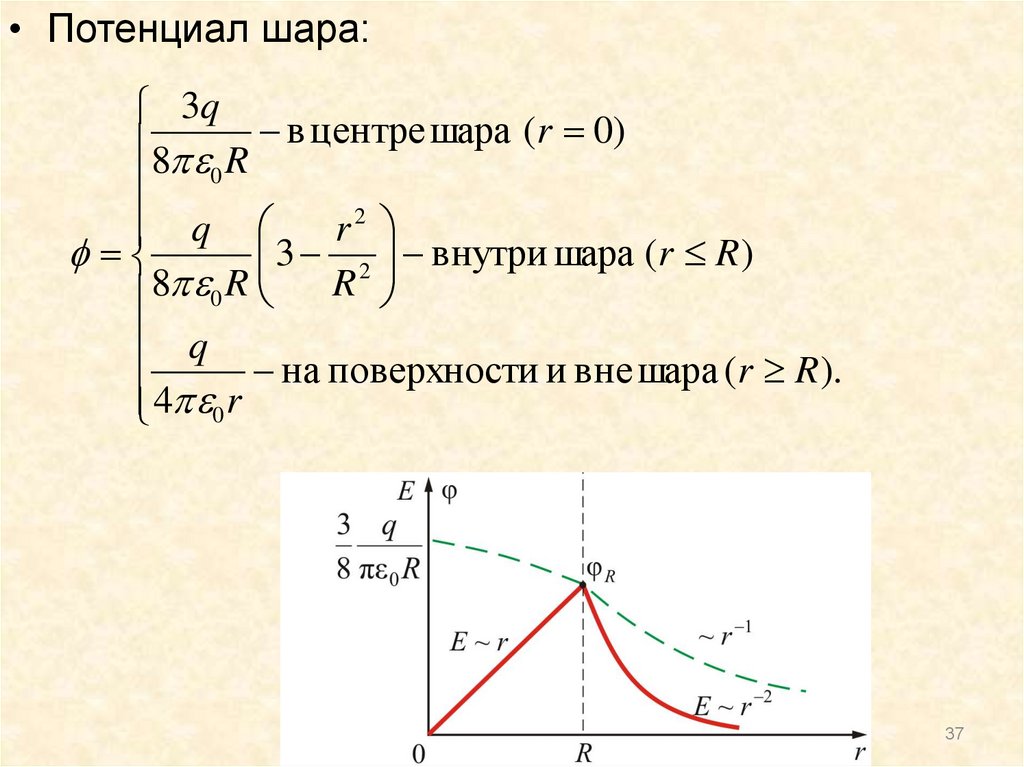
37.

• Потенциал шара:
3q
8 R в центре шара (r 0)
0
q
r2
3 2 внутри шара (r R )
R
8 0 R
q
на поверхности и вне шара (r R ).
4 0 r
37

38.

• Из полученных соотношений можно сделать
следующие выводы:
• С помощью теоремы Гаусса сравнительно просто
можно рассчитать Е и φ от различных заряженных
поверхностей.
• Напряженность поля в вакууме изменяется
скачком при переходе через заряженную
поверхность.
• Потенциал поля – всегда непрерывная функция
координат.
38