Электростатика. Проводники и диэлектрики в электрическом поле

1. Электростатика. Проводники и диэлектрики в электрическом поле

2. Применения теоремы Гаусса

1. Электростатическое поле равномерно
заряженной сферы.
2. Электростатическое поле равномерно
заряженного цилиндра.
3. Электростатическое поле равномерно
заряженной бесконечной плоскости.
4. Электростатическое поле равномерно
заряженного шара.

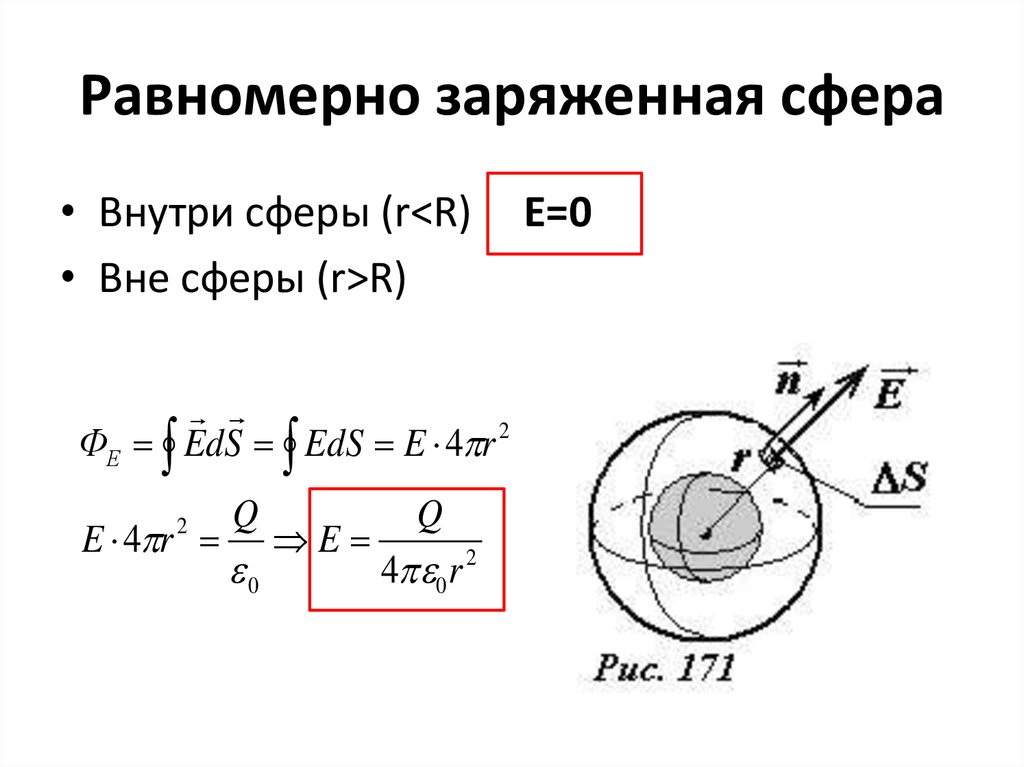
3. Равномерно заряженная сфера

• Внутри сферы (r<R)
• Вне сферы (r>R)
ФЕ EdS EdS E 4 r 2
Q
Q
E 4 r E
0
4 0 r 2
2
Е=0

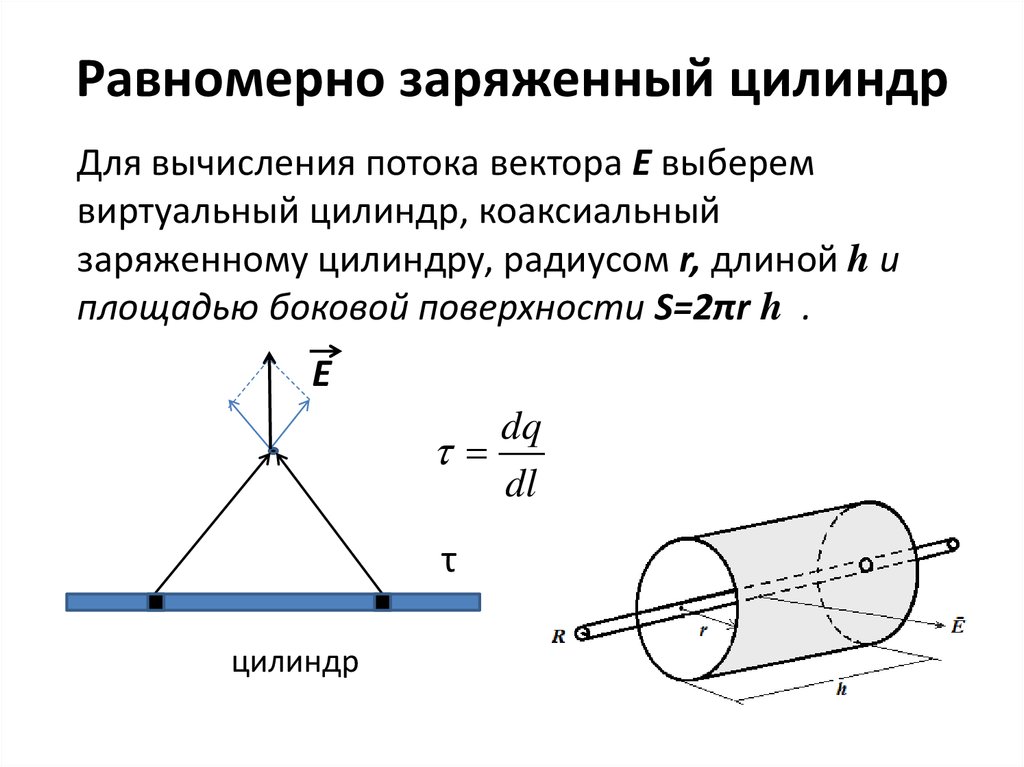
4. Равномерно заряженный цилиндр

Для вычисления потока вектора Е выберем
виртуальный цилиндр, коаксиальный
заряженному цилиндру, радиусом r, длиной h и
площадью боковой поверхности S=2πr h .
E
dq
dl
τ
цилиндр

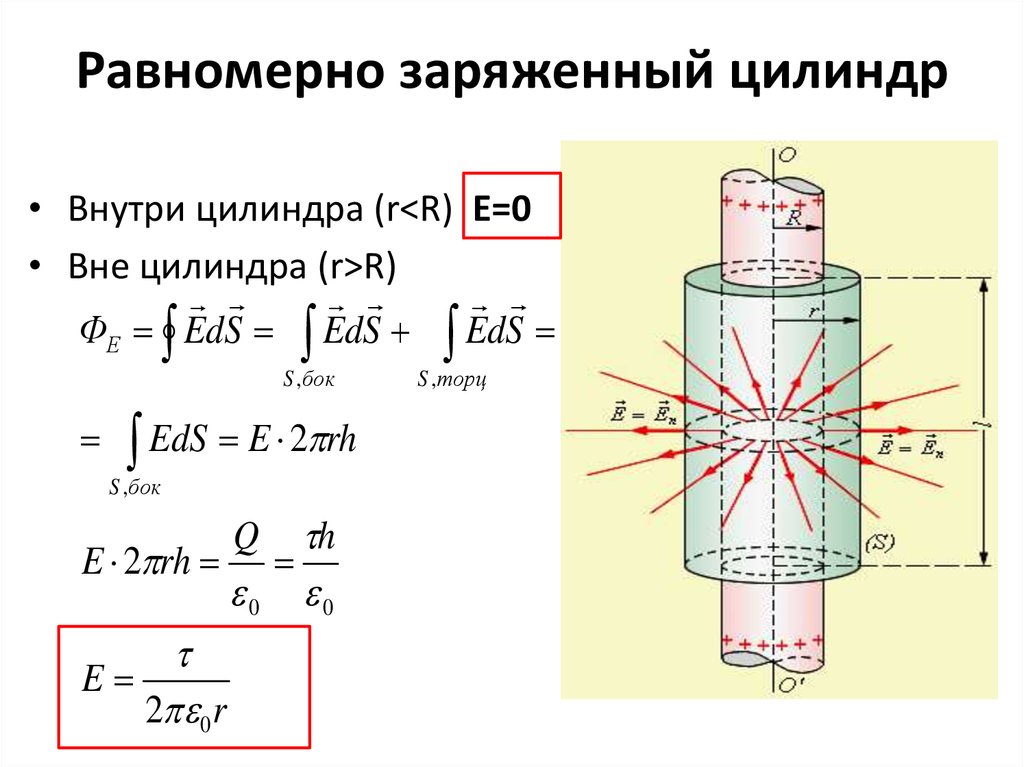
5.

Равномерно заряженный цилиндр
• Внутри цилиндра (r<R) Е=0
• Вне цилиндра (r>R)
ФЕ E d S E d S E d S
S ,бок
EdS E 2 rh
S ,бок
Q h
E 2 rh
0 0
E
2 0 r
S , торц

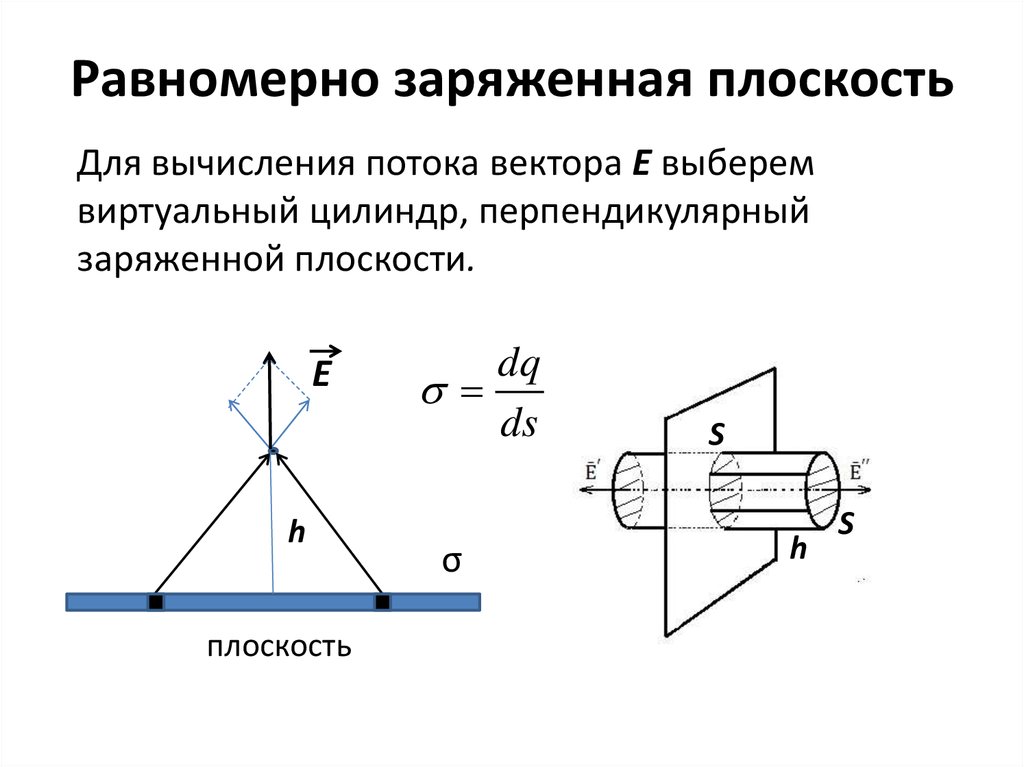
6. Равномерно заряженная плоскость

Для вычисления потока вектора Е выберем
виртуальный цилиндр, перпендикулярный
заряженной плоскости.
E
h
плоскость
dq
ds
σ
S
h
S

7. Равномерно заряженная плоскость

ФЕ E d S
2
Ed S
S ,бок
EdS 2 E S
S , торц
Q S
2E S
0 0
E
2 0
EdS
S , торц

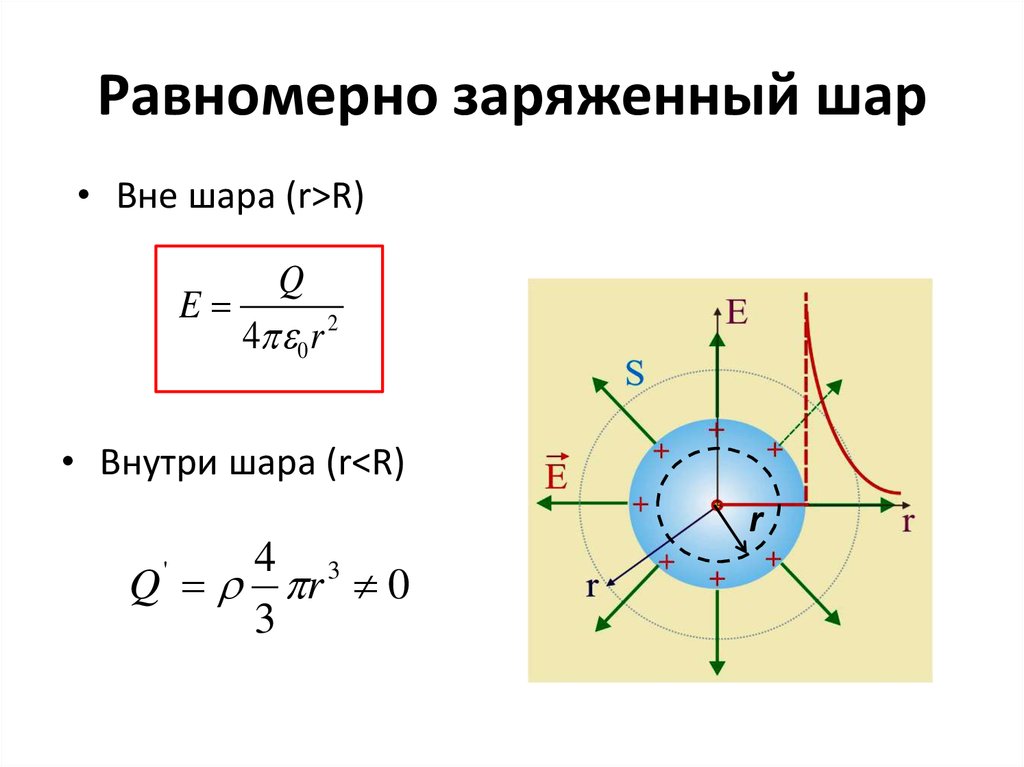
8. Равномерно заряженный шар

• Вне шара (r>R)
Q
E
4 0 r 2
• Внутри шара (r<R)
4 3
Q r 0
3
'
r

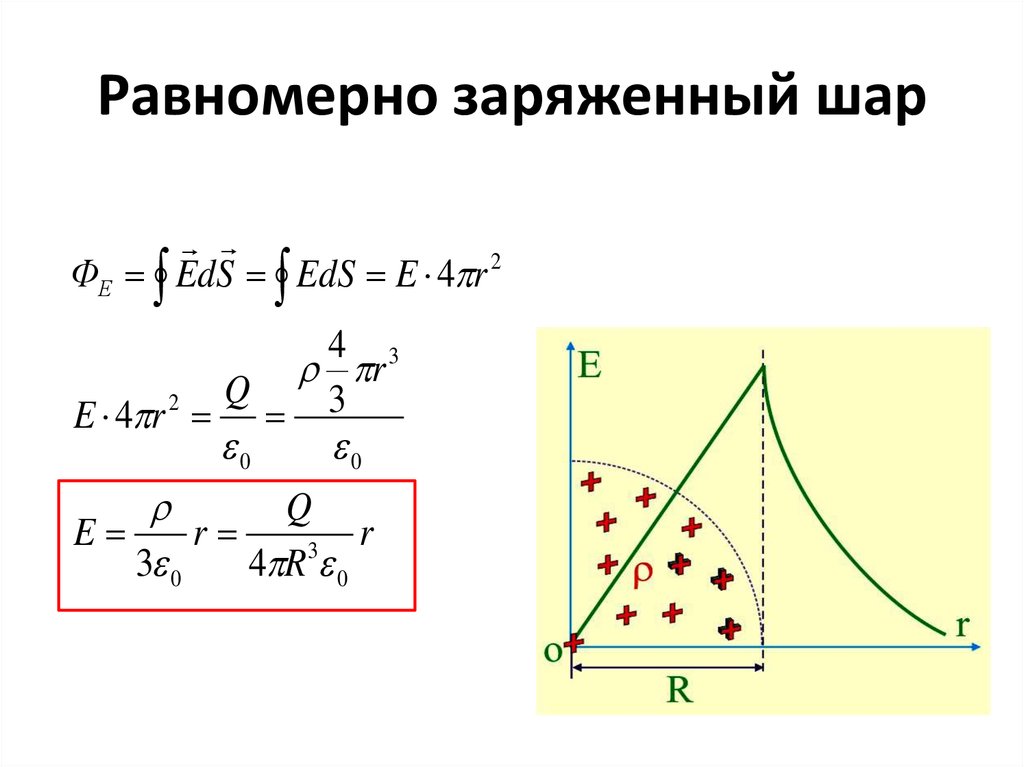
9. Равномерно заряженный шар

ФЕ EdS EdS E 4 r 2
4 3
r
Q
E 4 r 2 3
0
0
Q
E
r
r
3
3 0
4 R 0

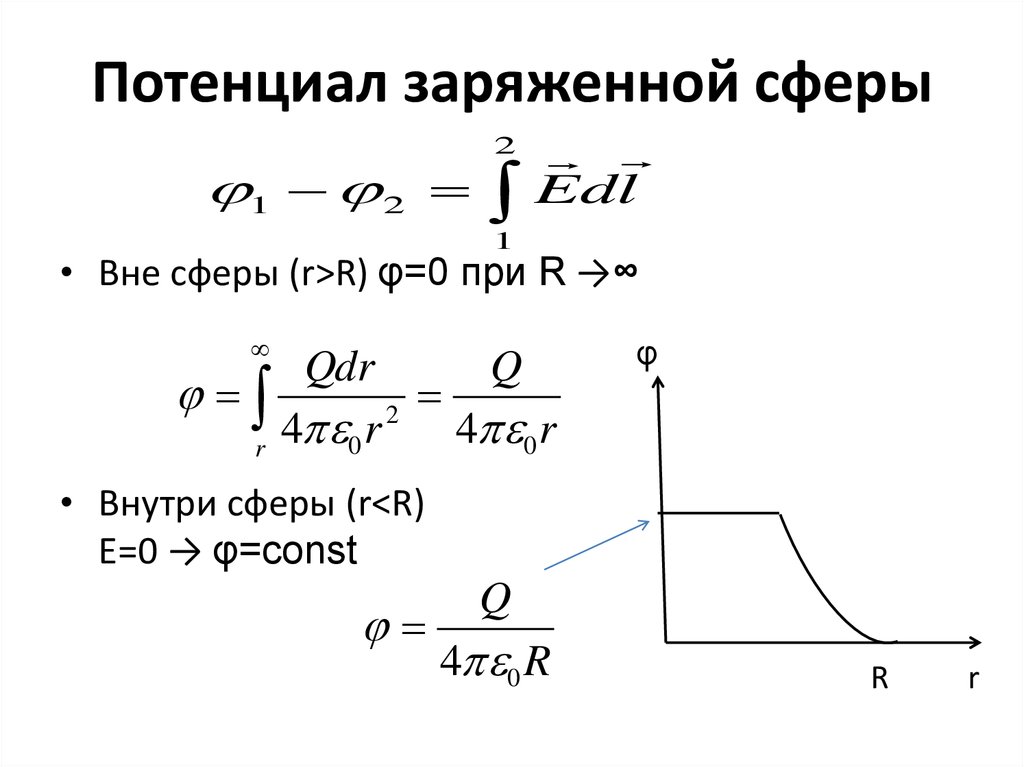
10. Потенциал заряженной сферы

1 2
2
Edl
1
• Вне сферы (r>R) φ=0 при R →∞
Qdr
Q
2
4 0 r
4 0 r
r
φ
• Внутри сферы (r<R)
Е=0 → φ=const
Q
4 0 R
R
r

11. Электроёмкость

Q
4 0 R
C 4 0 R
Q C
ёмкость сферы
• Ёмкость измеряется в Фарадах. Ёмкостью в 1 Ф обладает
шар радиуса 9 109 м (в 1.5 раз больше радиуса Земли).
• Для накопления значительных зарядов используются
конденсаторы.
• Конденсаторы состоят из двух проводников (обкладок),
помещенных на небольшом расстоянии друг от друга.
Заряды на обкладках равны по величине и
противоположны по знаку. Разность потенциалов между
обкладками называется напряжением.

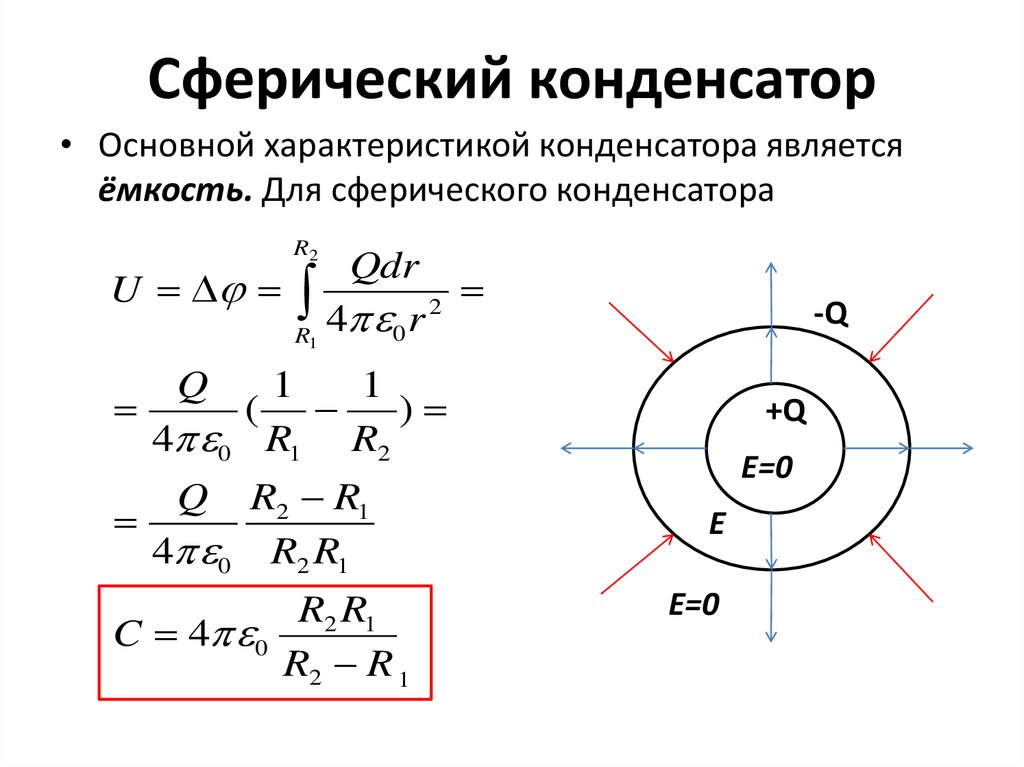
12. Сферический конденсатор

• Основной характеристикой конденсатора является
ёмкость. Для сферического конденсатора
R2
Qdr
U
2
4 0 r
R1
-Q
Q
1
1
(
)
4 0 R1 R2
R2 R1
4 0 R2 R1
Q
R2 R1
C 4 0
R2 R 1
+Q
E=0
E
E=0

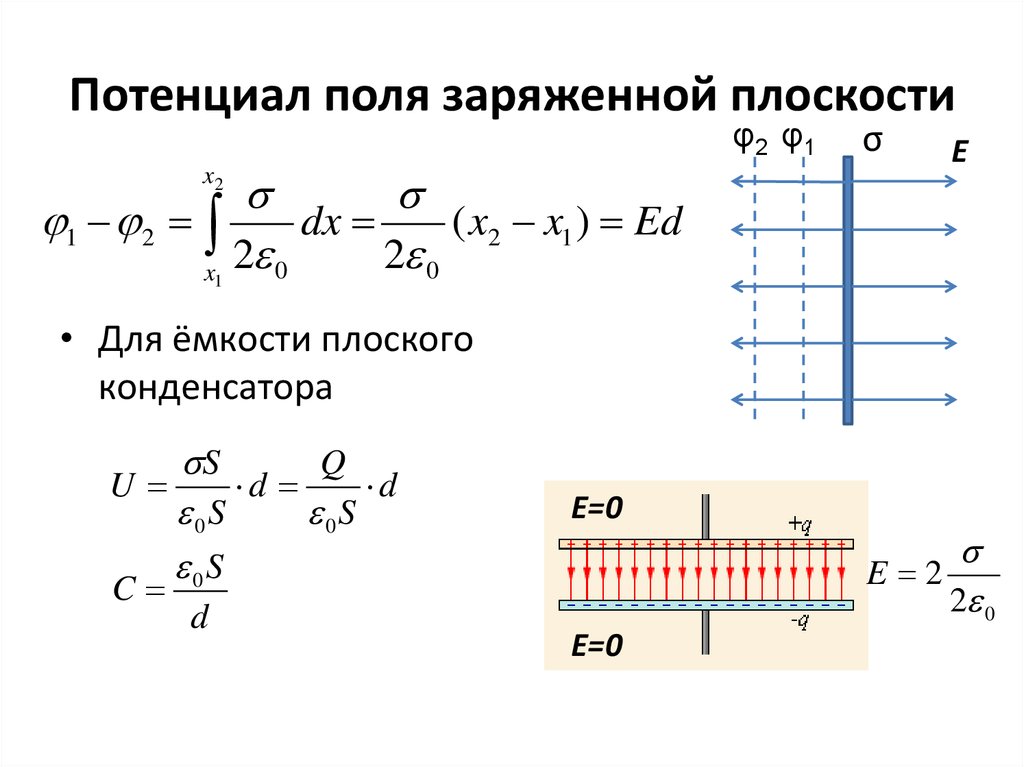
13. Потенциал поля заряженной плоскости

φ2 φ1
1 2
dx
( x2 x1 ) Ed
2 0
2 0
x
x2
σ
Е
1
• Для ёмкости плоского
конденсатора
S
Q
U
d
d
0S
0S
0S
C
d
E=0
E=0
E 2
2 0

14. Потенциальная энергия

W Q
• Для точечного заряда
• Если заряды распределены непрерывно
2
2
Q
1Q
С
W dQ dQ
C
2 C
2
V
V
• Для плоского конденсатора W 1 CU 2 1 0 S U 2
2
2 d
1
U Ed ; V Sd ; W 0 VE 2
2
W 1
w 0 E 2 объемная плотность энергии
V 2

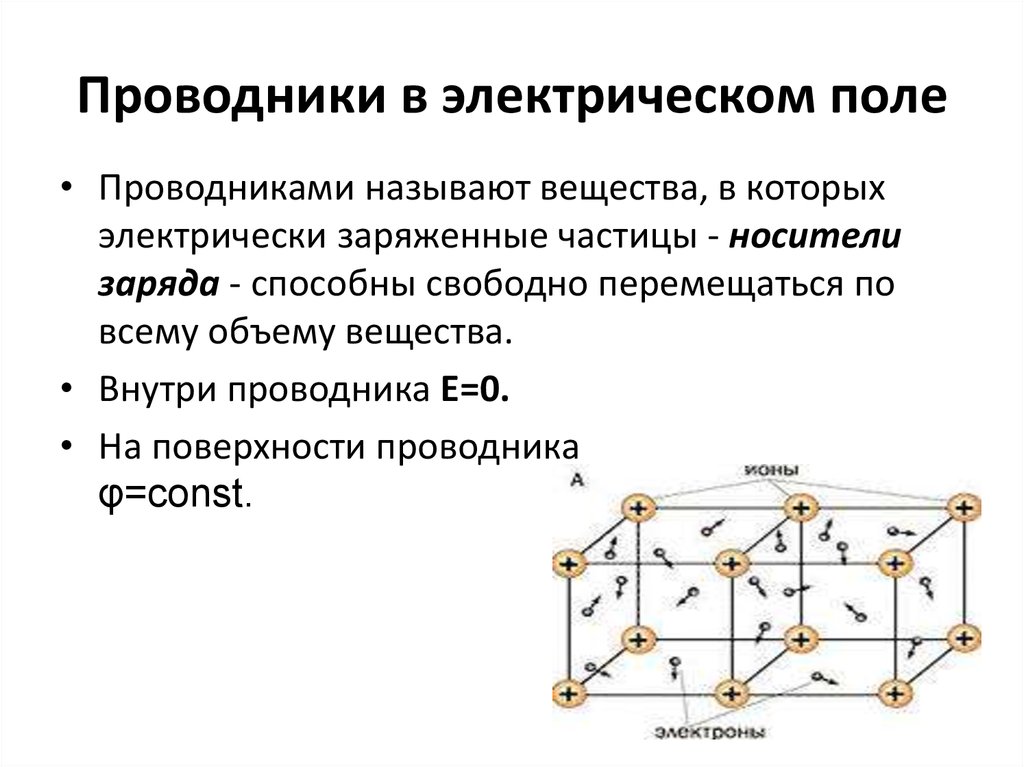
15. Проводники в электрическом поле

• Проводниками называют вещества, в которых
электрически заряженные частицы - носители
заряда - способны свободно перемещаться по
всему объему вещества.
• Внутри проводника Е=0.
• На поверхности проводника
φ=const.

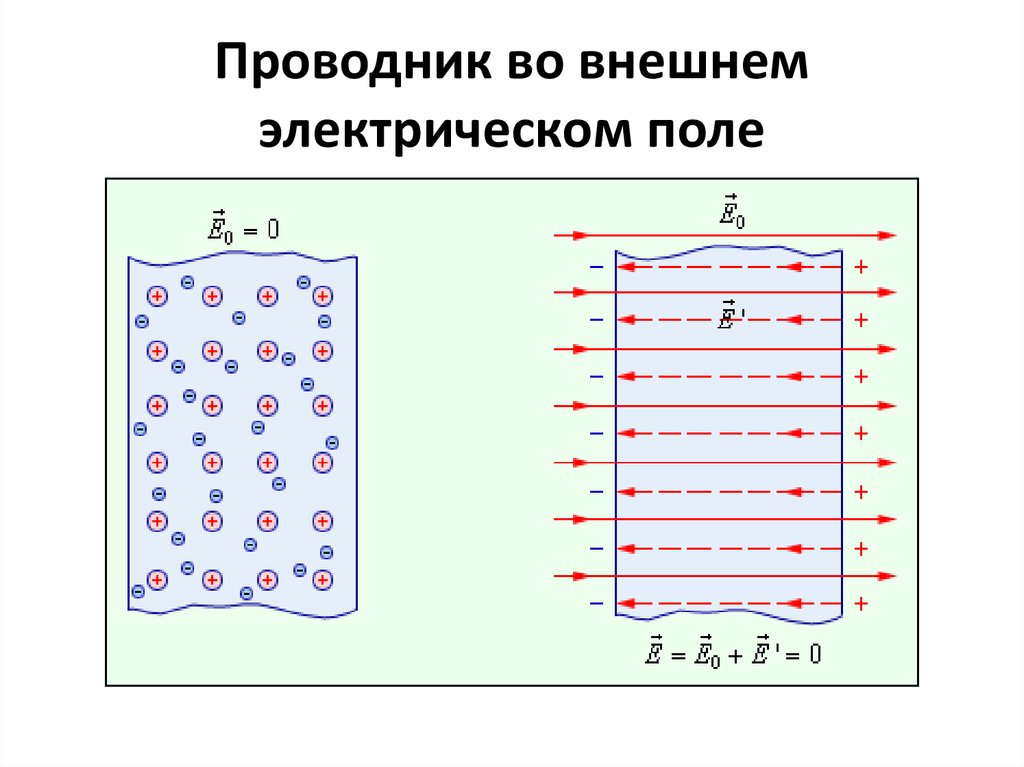
16. Проводник во внешнем электрическом поле

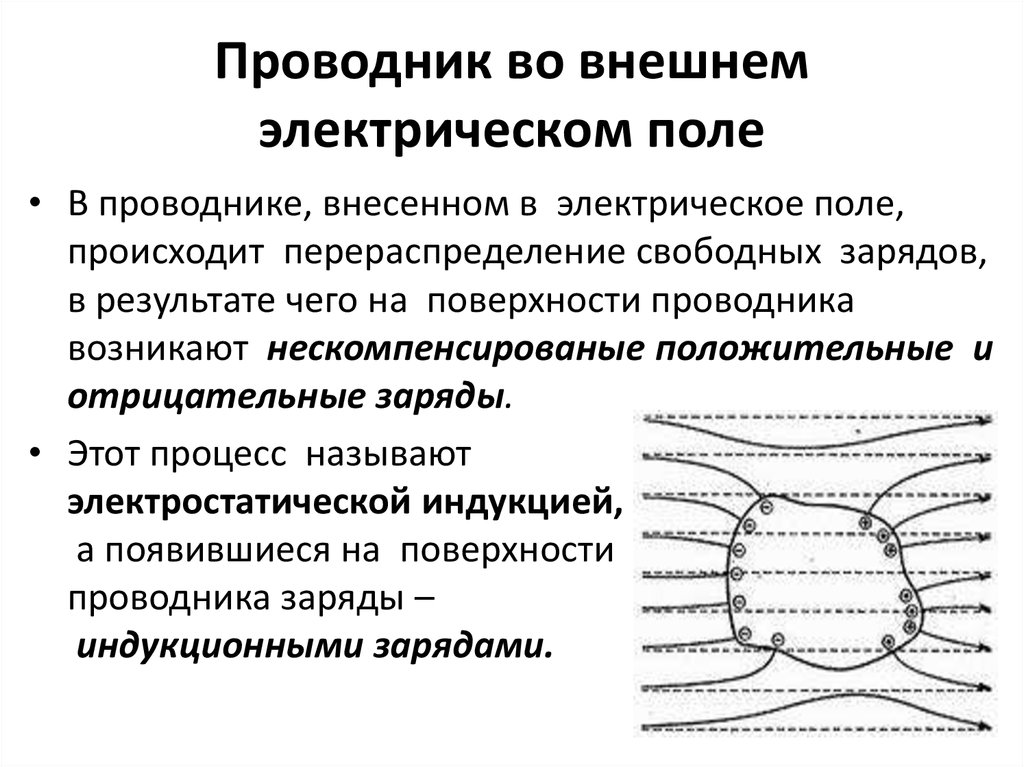
17. Проводник во внешнем электрическом поле

• В проводнике, внесенном в электрическое поле,
происходит перераспределение свободных зарядов,
в результате чего на поверхности проводника
возникают нескомпенсированые положительные и
отрицательные заряды.
• Этот процесс называют
электростатической индукцией,
а появившиеся на поверхности
проводника заряды –
индукционными зарядами.

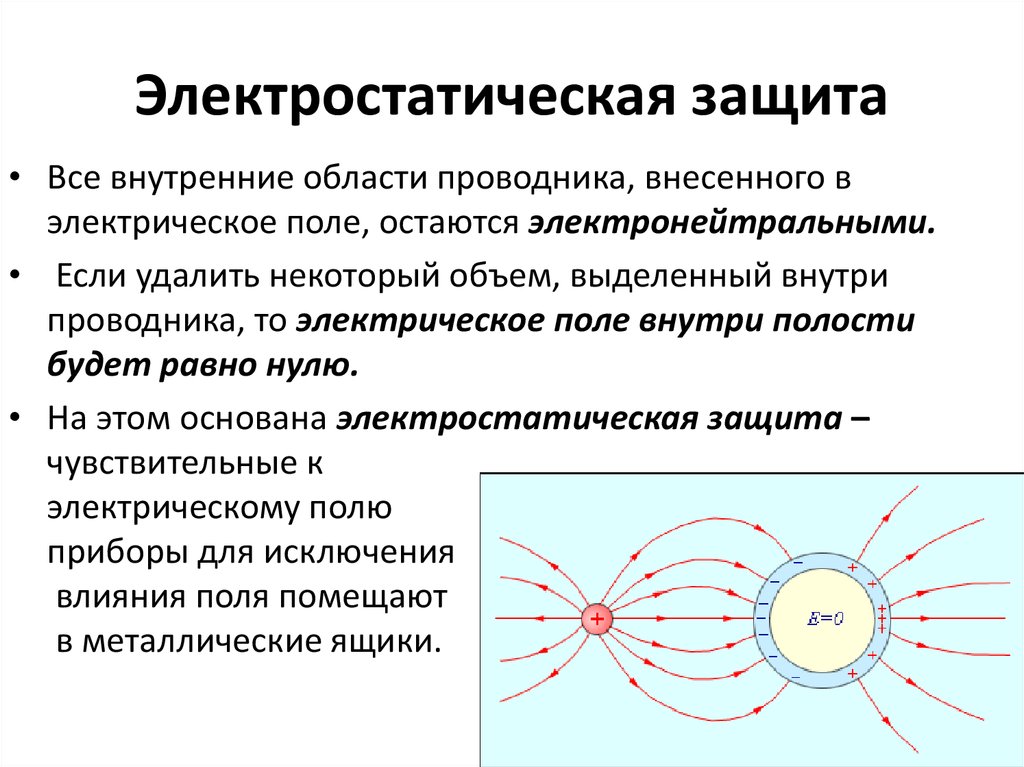
18. Электростатическая защита

• Все внутренние области проводника, внесенного в
электрическое поле, остаются электронейтральными.
• Если удалить некоторый объем, выделенный внутри
проводника, то электрическое поле внутри полости
будет равно нулю.
• На этом основана электростатическая защита –
чувствительные к
электрическому полю
приборы для исключения
влияния поля помещают
в металлические ящики.

19. Диэлектрики во внешнем электрическом поле

• В отличие от проводников, в диэлектриках
(изоляторах) нет свободных электрических зарядов .
• Заряженные частицы в нейтральном атоме связаны
друг с другом и не могут перемещаться под
действием электрического поля по всему объему
диэлектрика.
• Связанные заряды создают электрическое поле,
которое внутри диэлектрика направлено
противоположно вектору напряженности внешнего
поля. Этот процесс называется поляризацией
диэлектрика.

20. Поляризация диэлектриков

• Молекулу диэлектрика рассматривают как
электрический диполь – нейтральную
совокупность двух зарядов, равных по модулю и
противоположных по знаку, расположенных на
некотором расстоянии друг от друга.
Е
p Qd
-Q
d
+Q
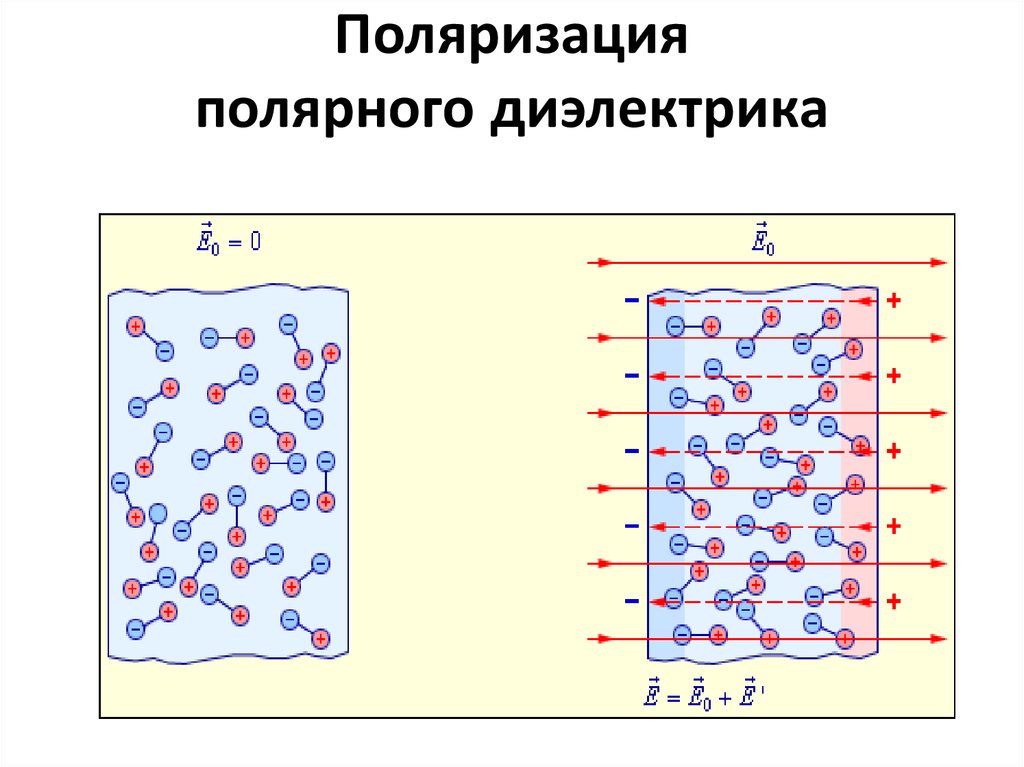
• Ориентационная или дипольная поляризация
возникает в случае полярных диэлектриков,
состоящих из молекул, у которых центры
распределения положительных и отрицательных
зарядов не совпадают.

21. Поляризация полярного диэлектрика

22. Поляризация неполярного диэлектрика

- +

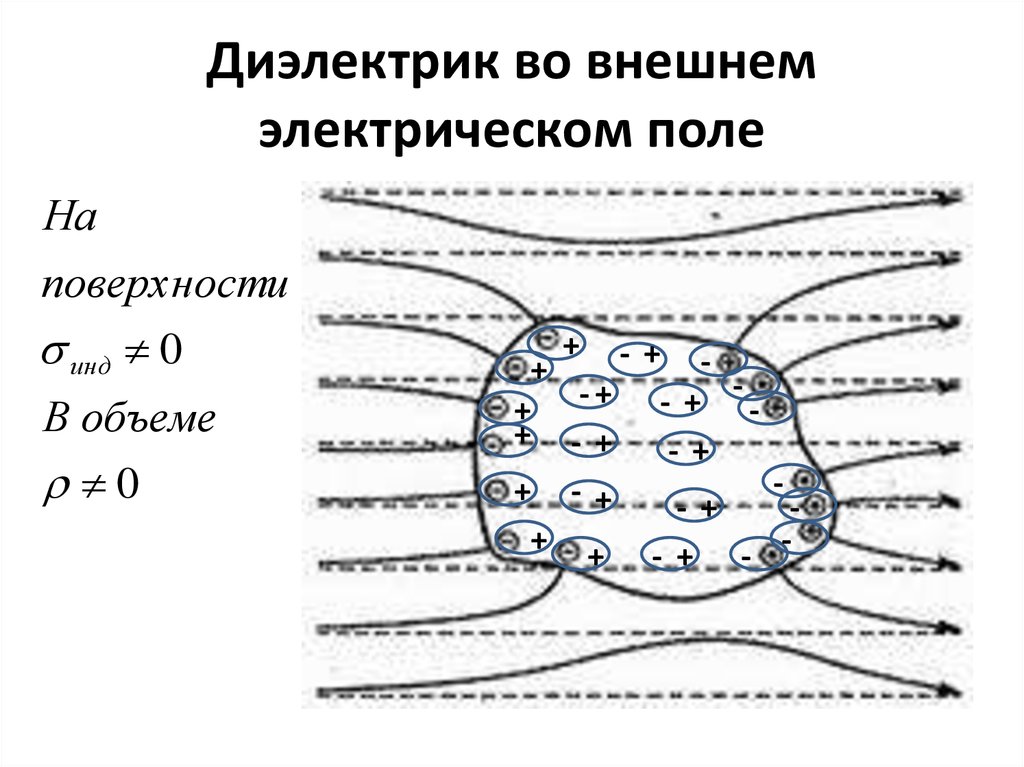
23. Диэлектрик во внешнем электрическом поле

На
поверхности
инд 0
В объеме
0
+
+
+
+
+
+ - + -+ - + -- +
- +
- +
- +
+ - + - -

24. Поляризованность, или вектор поляризации- это дипольный момент единицы объема диэлектрика.

pi qd i P
P 0 E , где
pi
V
'
E E0 E
κ-диэлектрическая восприимчивость диэлектрика.
Электрическое поле внутри диэлектрика
характеризуется вектором электрического смещения
(электрической индукции)

25. Электрическая индукция

D 0 E P 0 E 0 E
0 (1 ) E 0 E
ε-относительная диэлектрическая проницаемость среды.
В среде сила Кулона
q1q2
F
2
4 0 r
1

26.

Е0
l
+σ
• Внутри диэлектрика
напряженность ослабляется
в ε раз.
• Диэлектрик можно представить,
как совокупность диполей.
dS
- +
- +
dq ' dS ; dq ' dS
Дипольный момент
- +
dp ' dS l ; dp PdV
P
'
- +
-σ'
Е’
+σ'
-σ

27.

Е0
• Внутри диэлектрика
напряженность ослабляется
в ε раз.
'
+σ
-σ
P 0 E E E
0
- +
E0
E0
E E0 E E
1
- +
'
'
• Электрическая индукция
внутри диэлектрика совпадает
с индукцией внешнего поля.
D 0 E 0 E0 D0
- +
- +
-σ'
Е’
+σ'

28. Теорема Гаусса

• Поток электрического смещения через
замкнутую поверхность равен сумме
электрических зарядом, заключенных внутри
поверхности.
D 0 E
q
EdS
S
0
DdS q
S