Дробные рациональные уравнения

1.

Дробные рациональные
уравнения
Содержание
справочника

2.

Глава I. Краткий теоретический справочник.
Глава II. Алгоритмы решения типовых задач.
Глава III. Учебно-тренировочные задания.
Глава IV. По страницам истории.
Содержание
справочника
Завершение
работы

3.

Дробные рациональные уравнения
составлены из дробных выражений или дробных
и целых выражений.

4.

Алгоритм решения дробных
рациональных уравнений.
I способ
Дробь равна нулю в том случае, если числитель равен
нулю, а знаменатель отличен от нуля, т.е
Пример

5.

Алгоритм решения дробных
рациональных уравнений
1.
2.
3.
4.
II способ
Найти общий знаменатель дробей,
входящих в уравнение.
Умножить
обе части уравнения на
общий знаменатель.
Решить получившееся целое уравнение.
Исключить из его корней те числа,
которые обращают в ноль общий
знаменатель.
Пример

6.

Алгоритм решения дробных
рациональных уравнений
III способ
1.
2.
3.
4.
5.
Найти допустимые значения дробей, входящих
в уравнение.
Найти общий знаменатель дробей, входящих в
уравнение.
Умножить обе части уравнения на общий
знаменатель.
Решить получившееся уравнение.
Исключить корни, не входящие в допустимые
значения дробей уравнения.
Пример

7.

Решим уравнение:
I способ.
25-х²
3х
Решение:
= 0
25-х²
3х
Ответ: -5; 5.
= 0

8.

Решим уравнение:
II способ.
х-3
х-5
+
1
х
х+5
=
х(х-5)
1) ОЗ: х (х - 5)
х+5
х-3
1
2) х(х-5) ∙
=
х(х-5)∙
+х(х-5)
∙
х(х-5)
х-5
х

9.

3) Решим уравнение:
х(х -3)+ (х -5)= х +5
х2 -3х +х -5 –х -5 =0
х2 -3х -10 =0
Д =9 +40 =49>0, 2 корня
х1 =5
х2 = -2
4) Проверим являются ли -2 и 5 корнями уравнения.
Если х1 = 5, 5 (5-5)= 5∙0 = 0
Т.к. решение х = 5 обращает общий знаменатель в ноль,
значит корнем не является.
Если х2 = -2, (-2)∙ (-2 - 5) = 14 ≠0 – корень уравнения.
Ответ: -2.

10.

Решим уравнение:
III способ.
х-3
х-5
+
1) ОДЗ: х ≠ 0 и
2) ОЗ: х(х - 5)
1
х
х+5
=
х(х-5)
х – 5 ≠ 0,
х ≠ 5.
х+5
х-3
1
3) х(х-5) ∙
=
х(х-5)∙
+х(х-5)
∙
х(х-5)
х-5
х

11.

4)
5)
Решим уравнение:
х(х -3)+ (х -5)= х +5
х2 -3х +х -5 –х -5 =0
х2 -3х -10 =0
Д =9 +40 =49>0, 2 корня
х1 =5
х2 = -2
х1 = 5 не удовлетворяет ОДЗ, значит корнем не является.
х2 = -2 – корень уравнения.
Ответ: -2.
Вернуться к
содержанию
Завершение
работы

12.

Дорогой друг!
Тебе предоставляется возможность проверить
свои знания по теме
«Дробные рациональные уравнения».
Данный работа состоит из 5 заданий уровня А
и 3 задания уровня В.
Уровень А
Вернуться к
содержанию
Уровень В
Завершение
работы

13.

Уровень А
Решите уравнение:
№1.
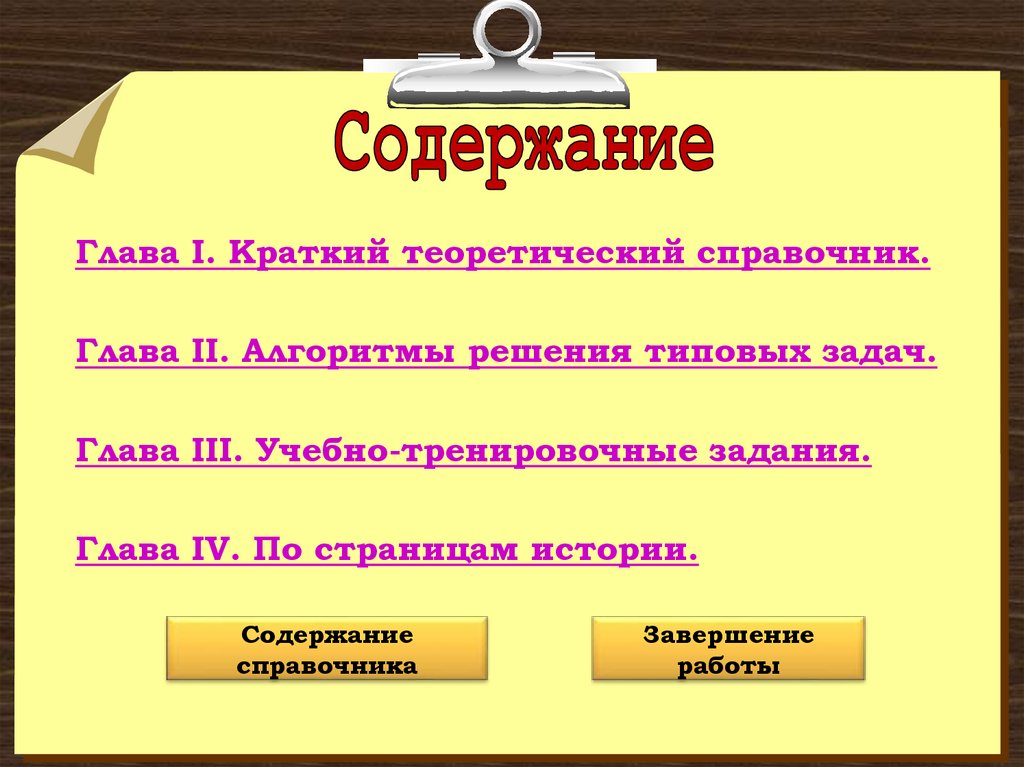
№2.
2х
3.
15 х
2х 1 4 х
.
3 х
х 1
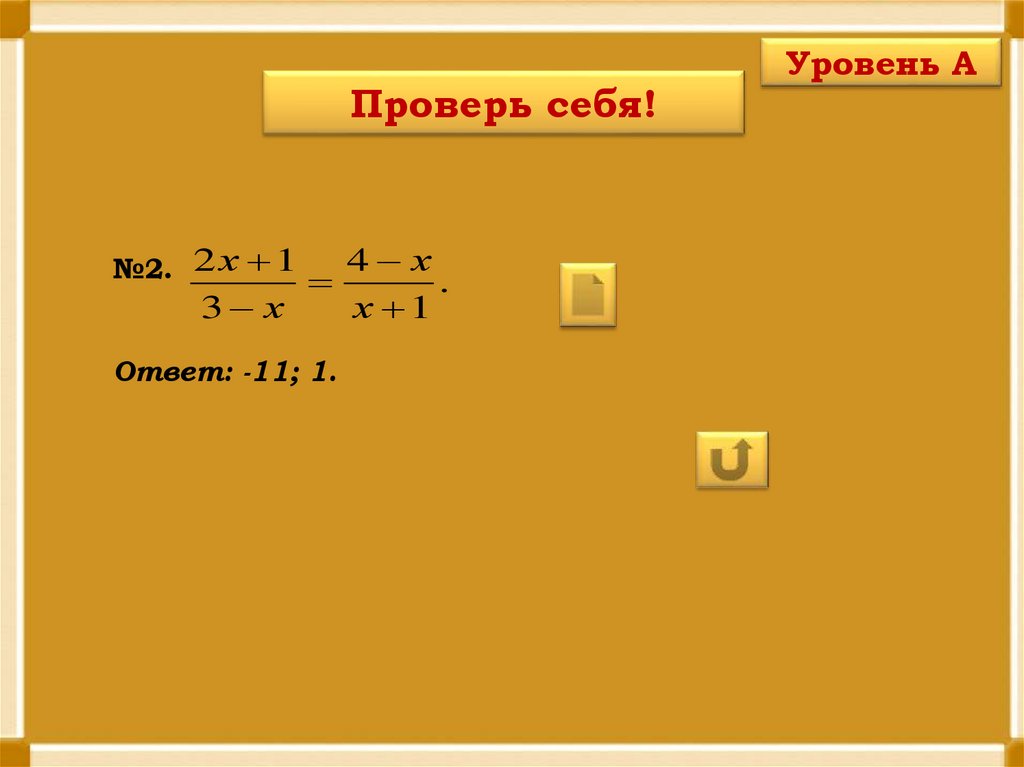
№3.
№4.
№5.
Проверь себя!
Проверь себя!
Проверь себя!
3х 2 х
3х 6
.
х 1 х 2 ( х 1)( х 2)
Проверь себя!
х 2 15 х 36
0.
х 9
Проверь себя!

14.

Решите уравнение:
Уровень В
№1.
Проверь себя!
№2.
Проверь себя!
№3.
Проверь себя!

15.

Проверь себя!
№1.
2х
3.
15 х
Ответ: х=-45.
Уровень А

16.

Проверь себя!
№2. 2 х 1 4 х .
3 х
Ответ: -11; 1.
х 1
Уровень А

17.

Проверь себя!
№3.
Ответ: 3;4.
Уровень А

18.

Проверь себя!
№4.
3х 2 х
3х 6
.
х 1 х 2 ( х 1)( х 2)
Ответ: -3.
Уровень А

19.

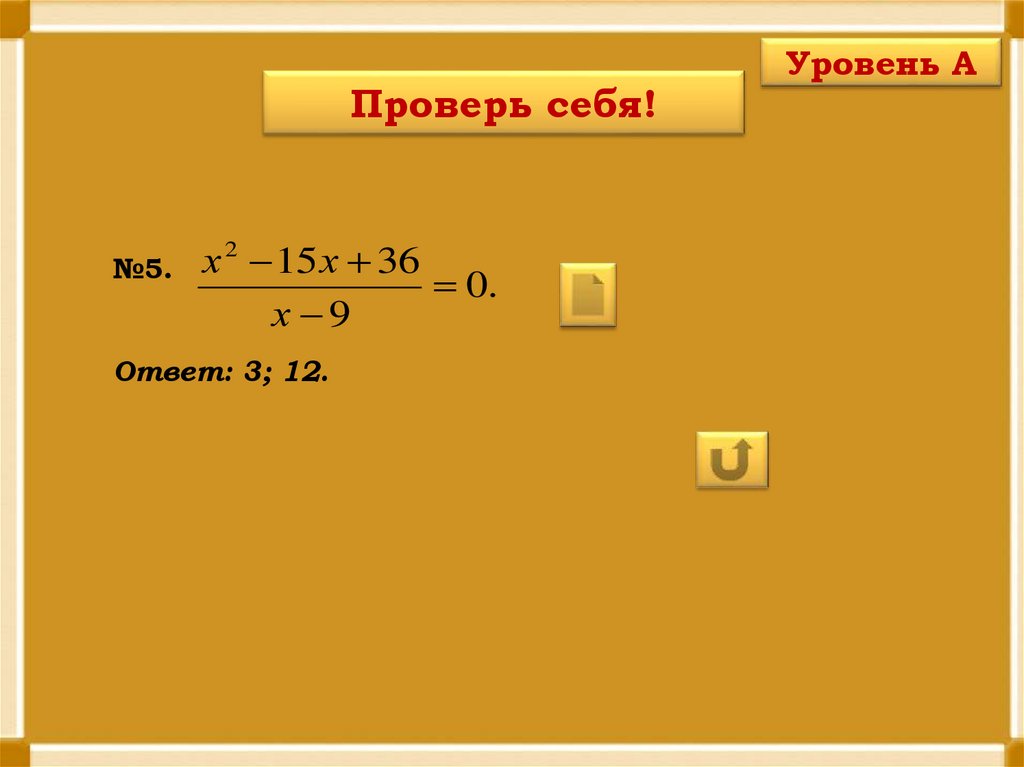
Проверь себя!
№5.
х 2 15 х 36
0.
х 9
Ответ: 3; 12.
Уровень А

20.

Проверь себя!
№1.
2х
3.
15 х
Решение:
ОЗ: 15+х
2х
(15 х) 3(15 х),
15 х
2х = 45 + 3х,
2х – 3х = 45,
-х = 45,
х = -45.
Если х = -45, то 15+(-45)= -30≠0, значит
х = -45 – корень уравнения.
Ответ : - 45.
Уровень А

21.

Проверь себя!
№2.
2х 1 4 х
.
3 х
х 1
Решение:
ОДЗ: 3-х≠0 и х +1≠0
х≠0
х≠ -1
ОЗ: (3-х)(х+1)
(2х + 1)(х+1)=(4-х)(3-х),
2х² + х + 2х + 1 = 12 – 3х – 4х + х²,
2х² + х + 2х + 1 - 12 + 3х + 4х - х² =0,
х² + 10х -11 =0,
по теореме обратной теореме Виета
х₁ + х₂ = - 10,
х₁∙ х₂ = -11
х₁=-11 – корень уравнения,
х₂=1 – корень уравнения.
Ответ : - 11; 1.
Уровень А

22.

Проверь себя!
№3.
Решение:
ОДЗ: х²≠0
х≠0
ОЗ: х²
12 +х² =7х,
х² - 7х + 12 =0
по теореме обратной теореме Виета
х₁ + х₂ = 7,
х₁∙ х₂ = 12
х₁= 3 – корень уравнения,
х₂= 4 – корень уравнения.
Ответ : 3; 4.
Уровень А

23.

Проверь себя!
2х
3х 6
№4. 3х
.
х 1 х 2 ( х 1)( х 2)
Уровень А
Решение:
ОЗ: (х-1)(х+2)
3х(х + 2) – 2х(х - 1)= 3х – 6,
3х² + 6х – 2х² + 2х -3х + 6 =0,
х² + 5х + 6 =0
D= 5² -4∙6 = 1>0, 2 корня.
х₁=
= -3,
х₂=
= -2.
Если х₁= -3, (-3-1)(-3 + 2) = 4≠0, значит х₁= -3 – корень уравнения.
Если х₂= -2, (-2 + 1)(-2 + 2)=0, значит х₂= -2 не является корнем
уравнения.
Ответ : -3.

24.

Проверь себя!
№5.
х 2 15 х 36
0.
х 9
Решение:
х² - 15х + 36 = 0,
D = 225 – 4∙ 36 = 81 >0, 2 корня
х₁ =
х₂ =
= 3,
= 12.
Ответ : 3, 12.
Уровень А

25.

Проверь себя!
№1.
Ответ: х= -3;
.
Уровень В

26.

Проверь себя!
№2.
Ответ: х= -4.
Уровень В

27.

Проверь себя!
№3.
Ответ: 2; 9.
Уровень В

28.

Проверь себя!
№1.
Решение:
ОДЗ: 3(х-2)(х+2)≠0
х - 2≠0 и х+2≠0
х≠2
х≠-2
(6-х) – 2∙3(х + 2)= 3(х² - 4),
6 – х - 6х – 12 = 3х² - 12,
- 3х² - 7х +6 =0,
3х² + 7х - 6 =0,
D = 7² - 4∙ 3∙(-6) = 49 + 72 =121>0, 2 корня
х₁ =
= -3,
х₂ =
.
корень уравнения
корень уравнения
Ответ : -3; .
Уровень В

29.

Проверь себя!
№2.
Решение:
ОДЗ: (2-х)(2+х)≠0
2-х≠0 и 2+х≠0
х≠2
х≠-2
36 + 2(2-х)(2+х)=(1-х)(2-х)+ 9(2+х),
36 +2(4-х²) = 2-2х –х + х² + 18 +9х,
36 + 8 -2х² -2 +3х –х²-18-9х=0,
-3х² -6х + 24 = 0,
х² +2х -8 = 0,
по теореме обратной теореме Виета х₁ + х₂ = -2,
х₁∙ х₂ = -8
х₁= 2 не является корнем уравнения,
х₂= -4 – корень уравнения.
Ответ : -4.
Уровень В

30.

Проверь себя!
Уровень В
№3.
Решение: Разложим на множители знаменатель каждой дроби:
х² +4х +3 = (х + 3 )(х +1 )
х² - х – 12 = (х + 3 )(х - 4 )
по теореме обратной теореме Виета по теореме обратной
теореме Виета
х₁ + х₂ = 1,
х₁ + х₂ =-4,
х₁∙ х₂ = -12
х₁∙ х₂ = 3
х₁ = -3; х₂ = 4
х₁ = -3; х₂ = -1
ОДЗ: (х+3)(х-4)(х+1)≠0
х+3≠0 и х-4≠0 и х+1≠0
х≠-3
х≠4
х≠-1
2(х+1)+6(х-4)=(х-4)(х+1),
2х +2 +6х-24=х²-4х+х-4,
-х² +11х -18 = 0,
х² -11х +18 = 0,
по теореме обратной теореме
Виета х₁ + х₂ = 11,
х₁∙ х₂ = 18.
х₁= 2 - корень уравнения,
х₂=9 – корень уравнения.
Ответ : 2;9.

31.

Знаменитый
французский
учёный
Франсуа
Виет(1540-1603)
был
по
профессии
адвокатом.
Свободное время он посвящал астрономии. Занятия
астрономией требовали знания тригонометрии и
алгебры. Виет занялся этими науками и вскоре пришёл
к выводу о необходимости их усовершенствования, над
чем и проработал ряд лет.
Благодаря его труду, алгебра становится общей
наукой об алгебраических уравнениях, основанной на
буквенном исчислении. Поэтому стало возможным
выражать свойства уравнений и их корней общими
формулами.

32.

Виет сделал много открытий, но сам он
больше всего ценил зависимость между
корнями и коэффициентами квадратного
уравнения, которая теперь называется
«теоремой Виета».
Франсуа
Виет
отличался
необыкновенной
работоспособностью.
Очень занятый при дворе французского
короля,
он
находил
время
для
математических работ, чаще всего за счёт
отдыха. Иногда, увлёкшись каким-нибудь
исследованиями,
он
проводил
за
письменным столом по трое суток подряд.
Завершение
работы

33.

Спасибо за работу с
электронным справочником!
Содержание
справочника
Вернуться к
содержанию