Similar presentations:
Дробно рациональные уравнения
1. Урок алгебры в 9 классе.
2. Тема урока: «Дробно рациональные уравнения»
3.
4. Повторение решения квадратных уравнений.
ах 2 вх с 0Д в 2 4ас
1) Если Д 0, уравнение имеет 2 различных корня.
2) Если Д 0, уравнение не имеет корней.
3) Если Д 0, уравнение имеет 1 корень.
5. Повторение.
1. Квадратное уравнение имеет 2 корня,если……
2. Квадратное уравнение имеет 2
равных корня (или ……. корень) ,
если……
3. Квадратное уравнение не имеет
корней, если……
4. Область допустимых значений
дробно-рационального уравнения
это…..
6. Повторение.
1.Как называется данное уравнение? Сколько корней имеет данное
уравнение?
2.
Скажите, какой степени это уравнение? Сколько корней имеет
данное уравнение?
3.
Скажите, какой степени это уравнение? Сколько корней имеет
данное уравнение?
4.
Как называется данное уравнение?
7. Указать ОДЗ
а) 2(1-х²) +3х -4 =0;б) х - 3= х² - х +1;
4
2
в) х² - х - 7 = х +8;
х
г) 2х - 4= 3__;
х² +1 х +1
д) 3х + 1= х ;
х -1
е)х-7 = √х+9
8. Устный счёт: Решите уравнения:
х 121 0х 11
х 49 0
Корней нет
х 17 0
х 17
х 5х 0
х 0; 5
2 х 16 х 0
х 0; 8
2
2
2
2
2
9. Сколько корней имеет уравнение:
2 х 3х 1 02 корня
4х 4х 1 0
1 корень
4а 5а 9 0
корней нет
2
2
2
10. Найти дискриминант квадратных уравнений
х 2х 3 05 или 7 4 или 16
х 3х 4 0
23
25
27
2 х 5х 3 0
1
3
5
2
2
2
11.
Если обе части уравнения являются рациональнымвыражением,
то
такие
уравнения
называют
рациональным уравнением.
Рациональные уравнения
Целые рациональные уравнения
2х 3
5 х;
5
2
х 6 х 8 0;
х 5 х 9
.
4
6
Дробно-рациональные уравнения
2х 3
4 х;
5 х
х2 6х 8
0;
х 2
х 5 х 9
.
4х
6
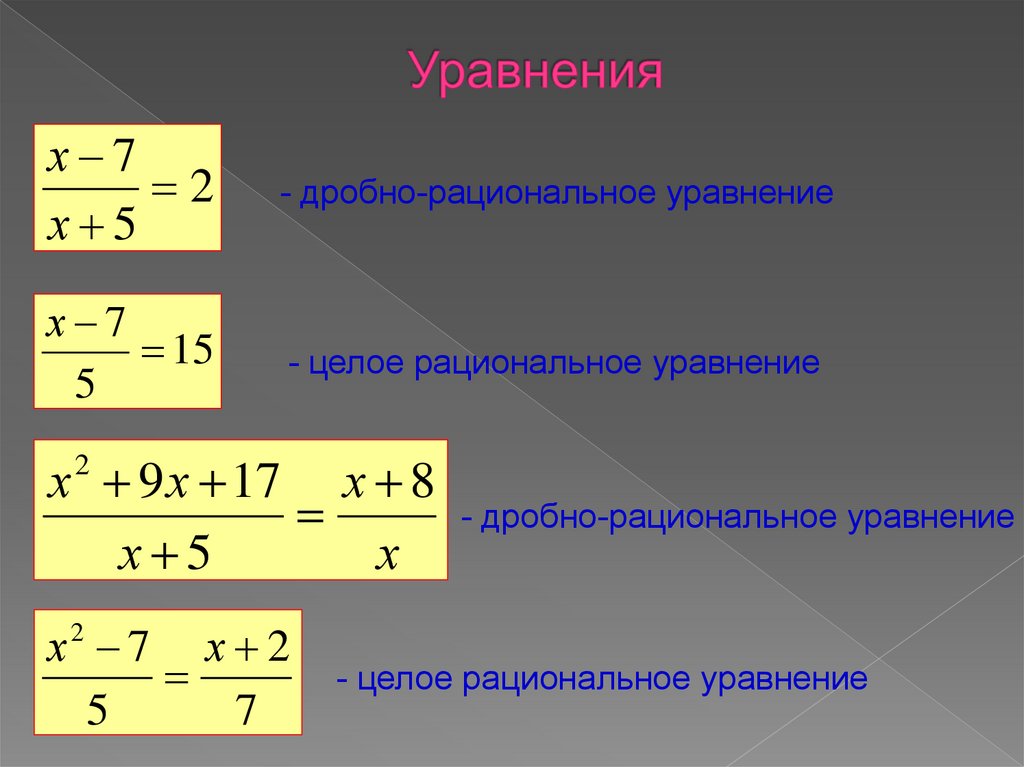
12. Уравнения
х 72
х 5
- дробно-рациональное уравнение
х 7
15
5
- целое рациональное уравнение
х 9 х 17 х 8
х 5
х
2
х 7 х 2
5
7
- дробно-рациональное уравнение
2
- целое рациональное уравнение
13. Алгоритм решения дробно-рациональных уравнений
• Найтиобщий знаменатель дробей, входящих в
уравнение;
• Умножить обе части уравнения на этот общий
знаменатель,
чтобы получить целое уравнение;
• Решить полученное целое уравнение;
• Исключить корни, обращающие каждый знаменатель в
нуль
или найти ОДЗ (Область допустимых значений
переменных в знаменателях данных дробей)
14.
15.
16.
17.
18.
19.
Повторение.20.
Решить уравнениеАлгоритм решения дробнорационального уравнения:
1) найти общий знаменатель
дробей, входящих в уравнение;
2) умножить обе части уравнения
на общий знаменатель;
3) решить получившееся целое
уравнение;
4) исключить из его корней те,
которые обращают в нуль
общий знаменатель.
Ответ: 3



















 mathematics
mathematics