Similar presentations:
Специальные главы математики
1.
СПЕЦИАЛЬНЫЕ ГЛАВЫМАТЕМАТИКИ
1 семестр
2.
Машинное обучение2
3.
Методы машинного обучения3
4.
МОДЕЛЬ ПРЕДСТАВЛЕНИЯ5.
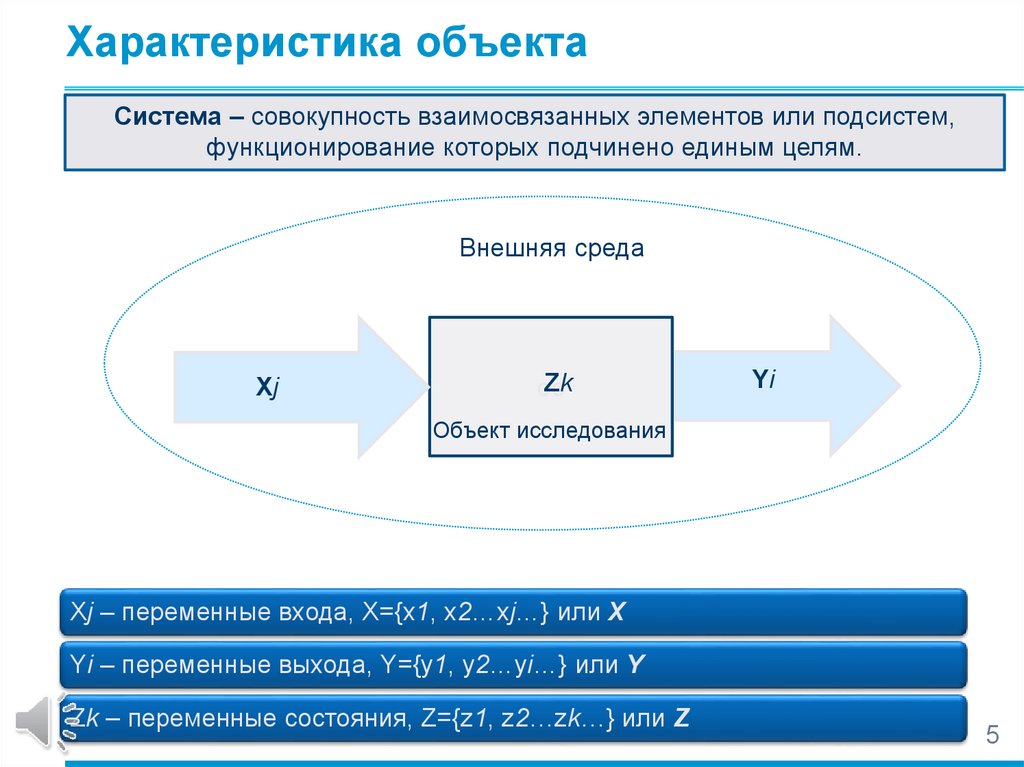
Характеристика объектаСистема – совокупность взаимосвязанных элементов или подсистем,
функционирование которых подчинено единым целям.
Внешняя среда
Xj
Zk
оо
Yi
Объект исследования
Xj – переменные входа, X={x1, x2…xj…} или X
Yi – переменные выхода, Y={y1, y2…yi…} или Y
Zk – переменные состояния, Z={z1, z2…zk…} или Z
5
6.
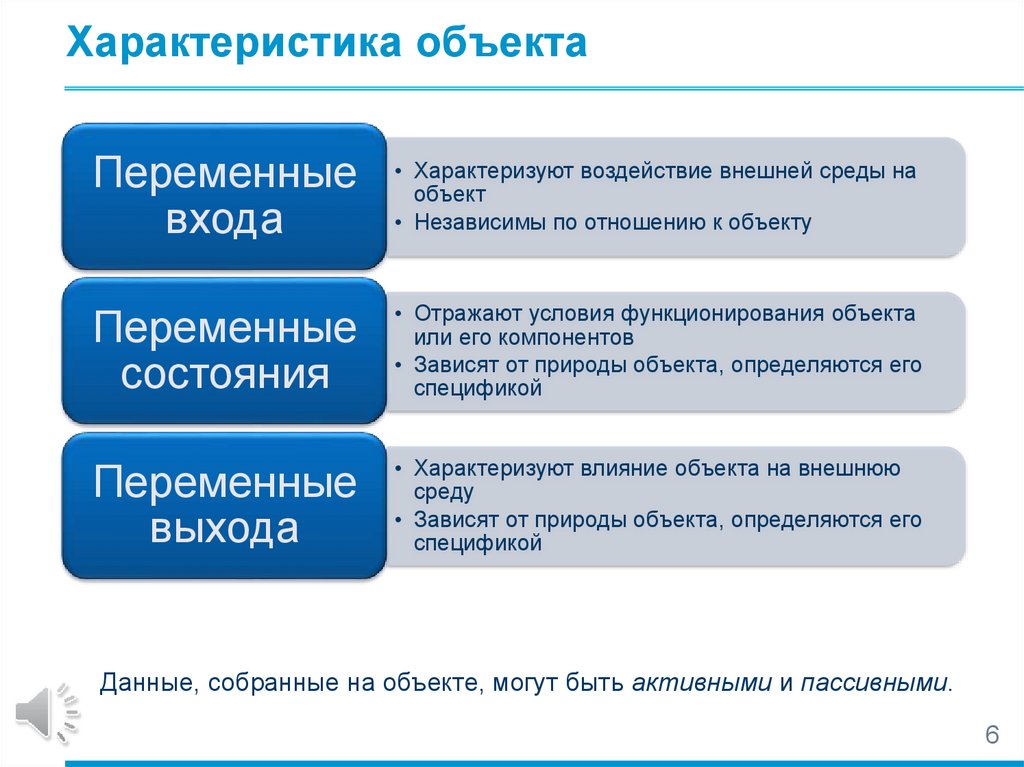
Характеристика объектаПеременные
входа
• Характеризуют воздействие внешней среды на
объект
• Независимы по отношению к объекту
Переменные
состояния
• Отражают условия функционирования объекта
или его компонентов
• Зависят от природы объекта, определяются его
спецификой
Переменные
выхода
• Характеризуют влияние объекта на внешнюю
среду
• Зависят от природы объекта, определяются его
спецификой
Данные, собранные на объекте, могут быть активными и пассивными.
6
7.
Значения переменных объектаКоличественные переменные
• числовое поле
Неколичественные переменные
• качественные значения
• символьные значения
• документы
• графы
• файлы
• алгоритмы
Область значений каждой переменной должна быть ограниченной,
счетной и обладать свойством однозначности.
7
8.
Цели и целевые функцииЦели исследования
• характеризуются
множеством
переменных
• отражают конечные
результаты
функционирования
объекта
Критерии качества
• представлены в
виде техникоэкономических и
организационных
показатели
• отражают меру
эффективности
функционирования
объекта
Целевые функции
• математическая
форма записи
критериев качества
на основе
переменных,
описывающих цели
исследования
Объективная составляющая
• определяется природой объекта исследования
Субъективная составляющая
• определяется ЛПР
8
9.
Общая постановка задачиНа основе компьютерной обработки имеющихся реальных данных, если
они подходят для этого, оценить степень влияния каждой из входных
переменных X и переменных состояния Z на целевые функции V(Y ) (или
хотя бы одну из них) с тем, чтобы в дальнейшем можно было бы
выбором их оптимального уровня добиться улучшения
функционирования данного объекта или использовать полученные
оценки в других исследованиях.
XUZ≡X
• независимые переменные
• объясняющие переменные
• факторы
• предикторы
• регрессоры
V(Y)≡Y
• зависимые переменные
• объясняемые переменные
• целевые функции
• отклики
9
10.
Задача машинного обучения10
11.
Классификация методовМетоды
статистического
анализа
Одномерные
методы
Метрические
данные
Многомерные
методы
Неметрические
данные
Зависимые
переменные
Взаимозависимые
переменные
Одна переменная
Несколько
переменных
Дисперсионный,
ковариационный,
дискриминантный
анализ, множественная
регрессия, кросстабуляция
Многомерный
дисперсионный,
ковариационный,
дискриминантный
анализ, анализ
корреляций
Зависимость
между
переменными
Межобъектное
сходство
Факторный анализ
Кластереный
анализ,
многомерное
шкалирование
11
12.
РЕГРЕССИОННЫЙ АНАЛИЗ12
13.
Основная литератураа) Основная литература
1.
2.
3.
Дрейпер Н., Смит. Г. Прикладной регрессионный анализ, 3-е
изд.:Пер. с англ. – М.: Издательский дом «Вильямс», 2007. – 912
с.
Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика.
Начальный курс. 6-е изд., перераб. и доп. - М.: Дело, 2004. — 576
с.
Вучков И. и др. Прикладной линейный регрессионный анализ. –
м.: Финансы и статистика, 1987 г. – 239с.
б) Дополнительная литература
1.
2.
3.
4.
5.
6.
Доугерти К. Введение в эконометрику. - М.: Инфра, 2001 г. – 402
с.
Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная
статистика: классификация и снижение размерности. - М.:
Финансы и статистика, -1988 г.
Введение в методы эконометрики. Сборник задач: Пер. с польск./
Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2004 г. –
248 с.
Эконометрика. Учебник/ Под ред. И.И.Елисеевой. - М.: Финансы
и статистика 2003 г. - 344 с.
Форман Дж. Много цифр: Анализ больших данных с помощью
Excel. – М.: Альпина Паблишер, 2016. – 461с.
Мюллер А., Гвидо С. Введение в машинное обучение с помощью
Python: Пер. с англ. – СПб.: ООО «Альфа книга», 2017. – 480 с.
13
14.
РегрессияРегрессия – зависимость
среднего значения какойлибо величины от некоторой
другой величины или
нескольких величин.
Тип корреляционной
(вероятностной,
статистической) зависимости
между величинами, не
имеющей функционального
характера.
M(Y|x)=y(x)
Значения ЦФ - количественные
Значения факторов – количественные
и неколичественные
14
15.
Построение регрессионной моделиI уровень
• y f ( x) f ' ( x)
• x X
n'
II уровень
• y x f ' ( x)
• f ( x) x x ... x x x x x ...
y f (x )
j 0
0
j
j
1 1
2 2
i
III уровень
n n
11 1 1
12 1 2
i
n'
n'
j 0
j 0
yˆ b j x j , yˆi b j x ji
ˆ j b j , M (b j ) j
y, j истинные значения
yˆ , b j расчетные (ттеоретические, оценочные) величины
j , b j регрессионные коэффициенты
15
16.
Эффекты влиянияФакторы (в чистом виде)
x1 , x2 ...x5 ...
Взаимодействия
x2 x3 , x1 x4 ...
Эффекты высоких степеней
x12 , x13 x2 , x52 x12 ...
Модели бывают линейные и нелинейные по факторам (x) и
по параметрам (b).
Линейность и нелинейность по факторам оговаривается особо и называется
порядком модели.
Пример:
yˆ b1e
b2 x1
b3 x2
16
17.
ПримерЗаписать общий вид аппроксимирующего полинома ЦФ, если известно,
что она зависит от трех факторов в чистом виде, их парных линейных
взаимодействий и эффекта третьей степени первого фактора.
17
18.
ПримерЗаписать общий вид аппроксимирующего полинома ЦФ, если известно,
что она зависит от трех факторов в чистом виде, их парных линейных
взаимодействий и эффекта третьей степени первого фактора.
Решение:
yˆ b0 b1 x1 b2 x2 b3 x3 b12 x1 x2 b13 x1 x3 b23 x2 x3 b111 x13
n'
b0 b1 x1 b2 x2 b3 x3 b4 x4 b5 x5 b6 x6 b7 x7 b j x j
j 0
n 3, n' 7
18
19.
Метод наименьших квадратовy 0 1 x1 0 1 x , yˆ b0 b1 x
ŷi
yi
b0
Диаграмма рассеяния
x1i xi
b j регрессионные коэффициенты, параметры модели
19
20.
Система нормальных уравненийei остаток для yi
ei yi yˆi yi b0 b1 x
Q ei2 ( yi b0 b1 x) 2
i
i
Q функция потерь( риска)
Решается задача :
Q min
xi , yi известные величины
b j неизвестные величины
N
Q
b 2 ( yi b0 b1 x) 0
0
i 1
N
Q
2 ( yi b0 b1 xi ) xi 0
b1
i 1
N
N
yi Nb0 b1 xi 0
i 1
i 1
N
N
N
2
y x b
x
b
x
i i
0 i
1 i 0
i 1
i 1
i 1
bj - МНК-оценка j-го коэффициента в уравнении регрессии.
Коэффициент регрессии bj - это абсолютная величина, на которую в
среднем изменяется величина ЦФ при изменении j-го фактора на
единицу измерения, если все остальные факторы в модели остаются
неизменными.
20
21.
Основные предпосылки классического ЛРА1. i случайная величина
yi f ( x) yi случайная величина
2. имеет нулевое математичское ожидание
3. некоррелированны и имеют одинаковую
дисперсию 2
4. имеет нормальное распеределение
~ N (0, 2 ), cov( i , l ) 0
5. Матрица регрессоров X - неслучайна
Классическая схема линейного регрессионного анализа – это процедура,
которая удовлетворяет всем предположениям.
21
22.
Задание 2. Линеаризация.Некоторые зависимости в химических реакциях выражаются уравнениями
вида:
a
4
z a1 1 2 2a3 e 3
a
Линеаризовать модель, привести ее к стандартному виду.
22
23.
Задание 2. Линеаризация.Некоторые зависимости в химических реакциях выражаются уравнениями
вида:
a
4
z a1 1 2 2a3 e 3
a
Линеаризовать модель, привести ее к стандартному виду.
Решение: прологарифмируем обе части уравнения:
ln z ln a1 a2 ln 1 a3 ln 2
Отсюда:
Тогда:
a4
3
yˆ ln z , b0 ln a1 , b1 a2 , x1 ln 1
b2 a3 , x2 ln 2 , b3 a4 , x3
1
3
yˆ b0 b1 x1 b2 x2 b3 x3
23
24.
Представление исходных данныхМатрица уровней
i x0 x1 x2 … xj … xn xn+1 … xn’
1 1 x11 x21
2 1 x12 x22
… … … …
i 1 … …
… … … …
N 1 x1N x2N
…
…
…
…
…
…
xj1 … xn1 xn+11
xj2 …
…
xji …
…
xjN …
… xn'1
…
…
…
…
… xn'N
Матрица планирования
Расширенная матрица планирования
Матрица уровней
Матрица
регрессоров X
i – номер выборки (опыта), j – номер фактора (регрессора)
Сочетание (ji) однозначно определяет уровень фактора
f ( x) 0 1 x1 2 x2 ... n xn n 1 xn 1 ... n ' xn '
24
25.
Представление исходных данныхМатрица результатов
i
yik
1 y11 ,y12...y1k … y1n1
2 y21 ,y22...y2k … y2n2
…
…
i yi1 ,yi2...yik … yini
…
…
N yN1 ,yN2...yNk … yNnN


















































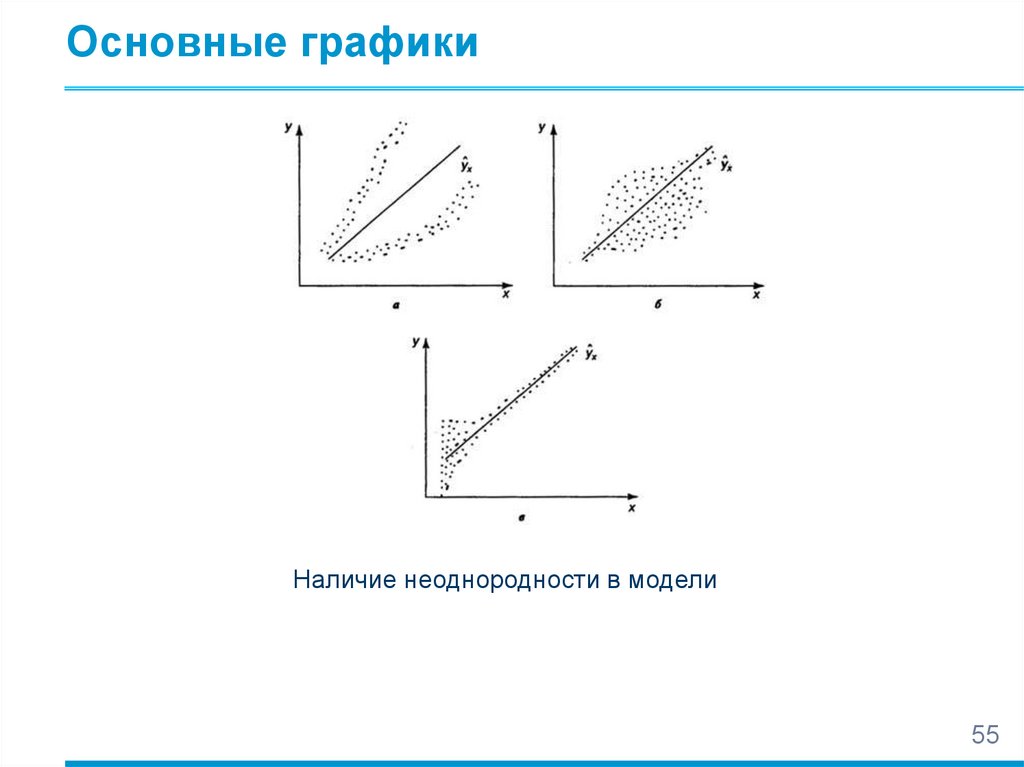

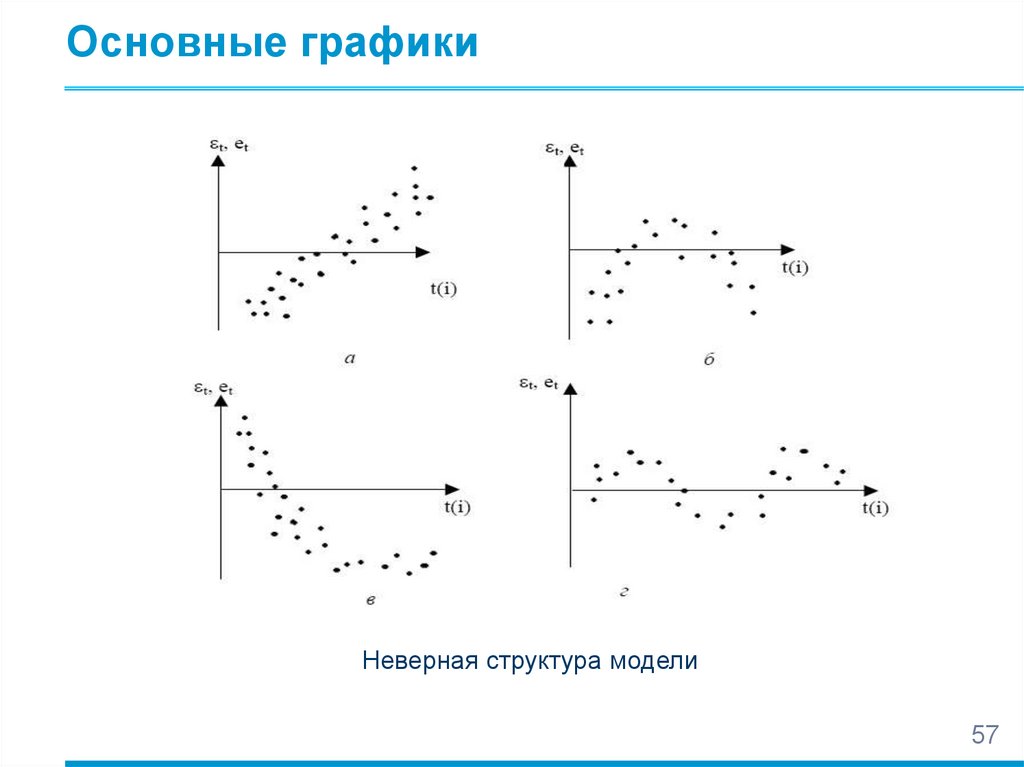






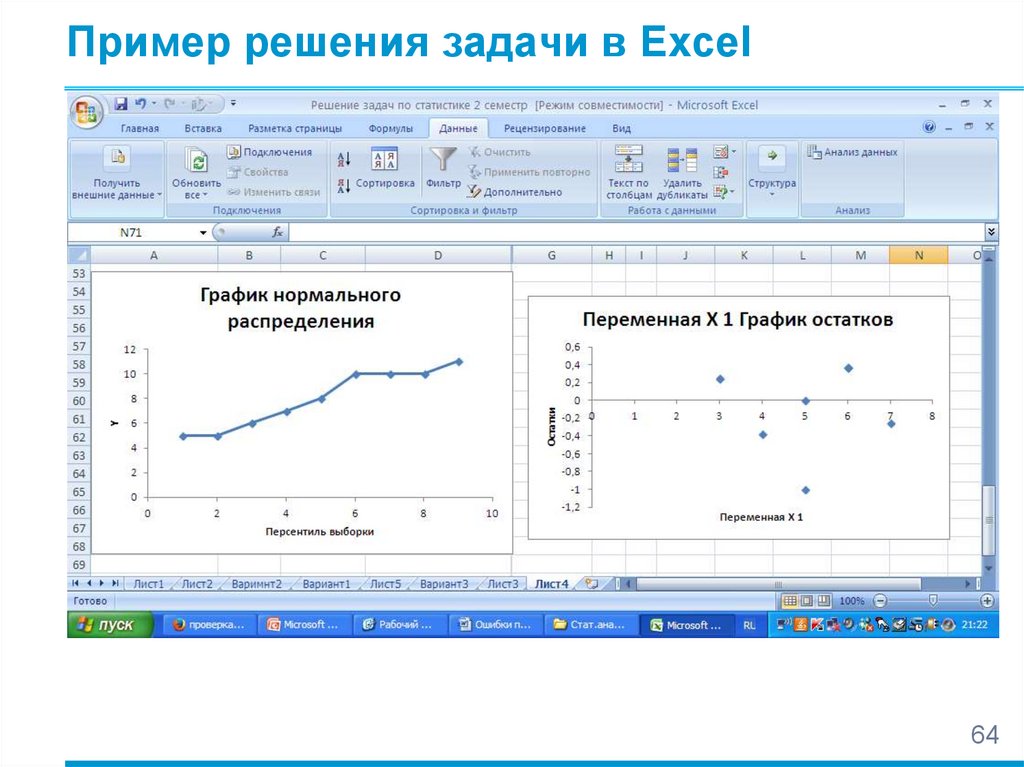


 mathematics
mathematics








