Similar presentations:
Вычислительная математика. Лекция 6
1. Вычислительная математика
Лекция 61
2. Темы занятий
Алгебра1. Решение систем линейных алгебраических
уравнений (СЛАУ).
2. Решение нелинейных алгебраических
уравнений.
Математический анализ
3. Приближение функций.
4. Вычисление определенных интегралов.
5. Решение дифференциальных уравнений.
2
3. Тема 3. Приближение функций
Обобщенная постановка задачи:Дано:
функция
y = f(x)
Найти:
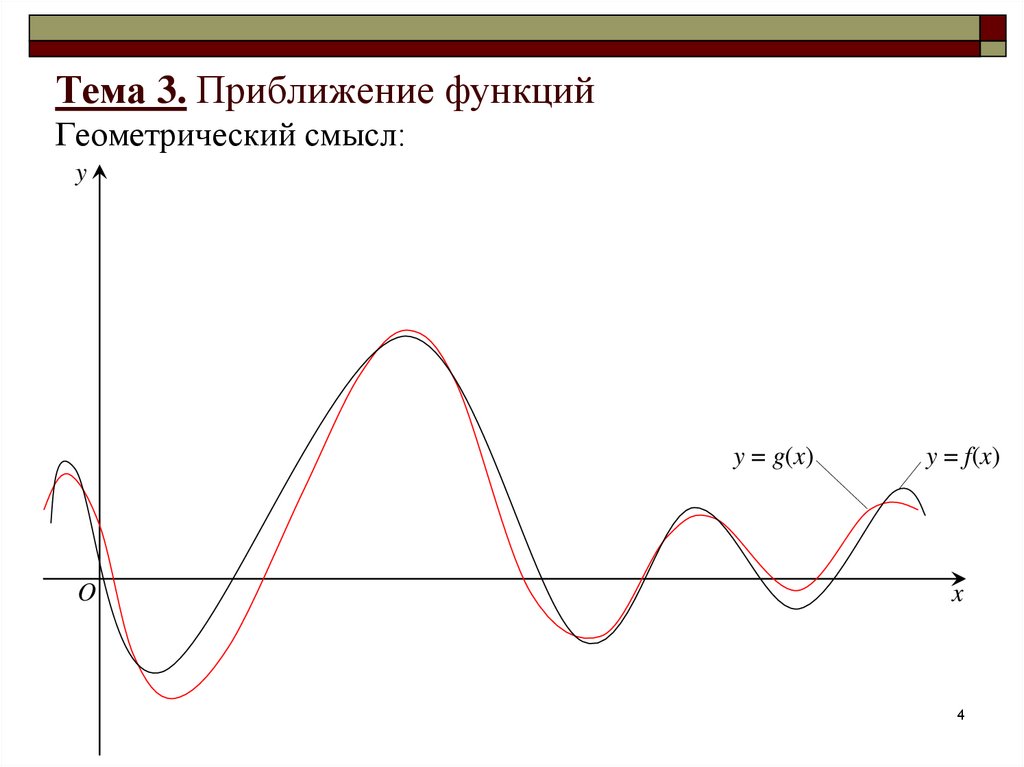
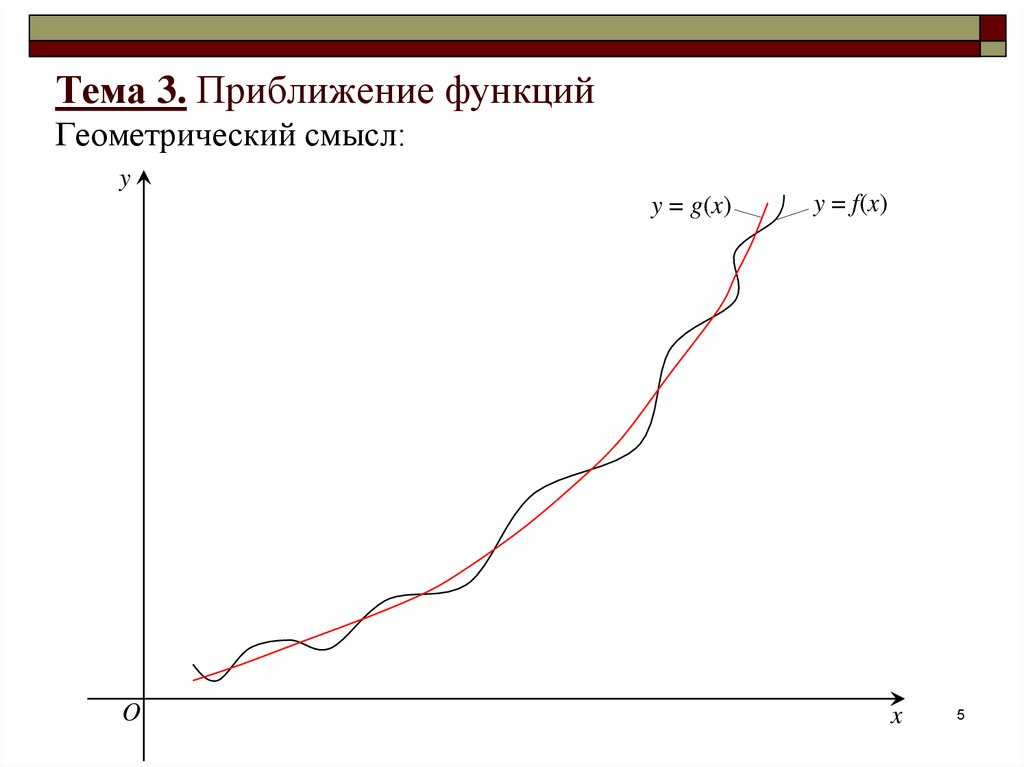
функцию y = g(x) такую, что f(x) ≈ g(x), то есть
погрешность приближения |f(x) – g(x)| достаточно мала
для всех х [a, b].
Нахождение функции y = g(x) называется задачей
аппроксимации функции y = f(x). Функция y = g(x)
называется аппроксимирующей функцией.
3
4. Тема 3. Приближение функций Геометрический смысл:
yy = g(x)
O
y = f(x)
x
4
5. Тема 3. Приближение функций Геометрический смысл:
yy = g(x)
O
y = f(x)
x
5
6. Тема 3. Приближение функций
Необходимость решения задачи аппроксимации возникает, когда:функция y = f(x) задана таблицей своих (в общем случае
приближенных) значений:
yi f(xi), i = 0, 1, 2, …, n;
~
x xi
при этом нужно вычислять значения функции y = f(x) в точках
(такая задача возникает при экспериментальном вычислении значений
функции y = f(x));
функция y = f(x) задана сложным аналитическим выражением,
затрудняющим вычисления; при этом требуется заменить сложную
функцию y = f(x) на более простую функцию y = g(x) (такая задача
возникает при необходимости многократного вычисления значений
функции y = f(x) или при необходимости выполнения операций над
функцией y = f(x), например, дифференцирования или интегрирования).
6
7. Тема 3.1 Аппроксимация по методу наименьших квадратов
Пусть аппроксимирующая функция имеет видy = Q(x, a0, a1, …, am),
где ai (i = 0, 1, …, m) – числовые параметры, значения которых
находятся из условия
n
2
S (a0 , a1 , , am ) Q( xi , a0 , a1 , , am ) yi min
i 0
Тогда значения параметров находятся из системы уравнений,
полученной из необходимого условия экстремума функции:
S
a 0;
0
S 0;
a
1
.......... .......... .
S 0.
am
7
8. Метод наименьших квадратов
ПустьQ(x, a0, a1, …, am) = a0 + a1x + a2 x2 + ... +am xm.
Тогда
2
j
S (a0 , a1 , , am ) a j xi yi
i 0 j 0
Следовательно,
n m
S
j
k
(a0 , a1 , , am ) 2 a j xi yi xi
ak
i 0 j 0
n
n
m
2 a0 a1 xi a2 xi2 ... am xim yi xik
i 0
n
2 a0 xik a1 xik 1 a2 xik 2 ... am xik m yi xik
i 0
n k
n k 1
n k m
n
2 xi a0 xi a1 ... xi am yi xik .
i 0
i 0
i 0
i 0
8
9. Метод наименьших квадратов
Таким образом, получена СЛАУ на нахождение значенийпараметров ai (i = 0, 1, …, m) имеет вид:
n
n
n 2
n m
(n 1)a0 xi a1 xi a2 ... xi am yi ;
i 0
i 0
i 0
i 0
n
n
n 2
n 3
n m 1
xi a0 xi a1 xi a2 ... xi am yi xi ;
i 0
i 0
i 0
i 0
i 0
n
n
n 3
n 4
n m 2
2
2
xi a0 xi a1 xi a2 ... xi am yi xi ;
i 0
i 0
i 0
i 0
i 0
......................................................................................................
n
n m 1
n m 2
n 2m
n m
m
x
a
x
a
x
a
...
x
a
y
x
1
i
2
i
m
i i .
i 0 i
i 0
i 0
i 0
i 0
i 0
9
10. Метод наименьших квадратов
В частном случае при m = 4 имеем СЛАУ :n
n
n 2
n 3
n 4
(n 1)a0 xi a1 xi a2 xi a2 xi a2 yi ;
i 0
i 0
i 0
i 0
i 0
n
n
n 2
n 3
n 4
n 5
xi a0 xi a1 xi a2 xi a2 xi a2 yi xi ;
i 0
i 0
i 0
i 0
i 0
i 0
n
n
n 3
n 4
n 5
n 6
2
2
xi a0 xi a1 xi a2 xi a2 xi a2 yi xi ;
i 0
i 0
i 0
i 0
i 0
i 0
n
n
n 4
n 5
n 6
n 7
3
xi a0 xi a1 xi a2 xi a2 xi a2 yi xi3 ;
i 0
i 0
i 0
i 0
i 0
i 0
n
n
n
n
n
n
4
5
6
7
8
x a x a x a x a x a y x 4 .
i 0 i 0 i 0 i 1 i 0 i 2 i 0 i 2 i 0 i 2 i 0 i i
10
11. Метод наименьших квадратов
Пусть m = 1, a0 = b, a1 = k.Тогда получим
n
n
(n 1)b xi k yi ;
i 0
i 0
n
n
n
x b x 2 k
yi xi .
i
i
i 0
i 0 i 0
Отсюда
c d c d
c d c d
k 11 2 122 1 , b 22 1 12 2 2 ,
c11c22 c12
c11c22 c12
где
n
n
n
n
i 0
i 0
c11 n 1, c12 xi , c22 x , d1 yi , d 2 yi xi .
i 0
i 0
2
i
11
12. Виды эмпирической зависимости
№Преобразование
переменных
1 Xi = xi ,
Yi = xiyi
Эмпирическая формула
y = α + β/x,
2 Xi = xi ,
Yi = 1/yi
y = 1/(αx + β), α = k, β = b
3 Xi = xi ,
Yi = xi /yi
y = x/(αx + β), α = k, β = b
4 Xi = xi ,
Yi = ln yi
y = αβx,
α = eb, β = ek
5 Xi = ln xi , Yi = yi
y = αln x + β,
α = k, β = b
6 Xi = ln xi , Yi = ln yi
y = αxβ,
α = eb, β = k
α = k, β = b
12
13. Метод наименьших квадратов
ПустьQ(x, a0, a1, …, am) = a0φ0(x) + a1φ1(x) + a2 φ2(x) + ... +am φm(x).
2
Тогда
n m
S (a0 , a1 , , am ) a j j ( xi ) yi
Следовательно,
i 0
j 0
n m
S
(a0 , a1 , , am ) 2 a j j ( xi ) yi k ( xi )
ak
i 0 j 0
n
2 a0 0 ( xi ) a1 1 ( xi ) a2 2 ( xi ) ... am m ( xi ) yi k ( xi )
i 0
n
2 a0 0 ( xi ) k ( xi ) a1 1 ( xi ) k ( xi ) a2 2 ( xi ) k ( xi ) ... am m ( xi ) k ( xi ) yi k ( xi )
i 0
n
n
n
n
2 0 ( xi ) k ( xi ) a0 1 ( xi ) k ( xi ) a1 ... m ( xi ) k ( xi ) am yi k (13xi ) .
i 0
i 0
i 0
i 0
14. Метод наименьших квадратов
Таким образом, получена СЛАУ уравнений на нахождениезначений параметров ai (i = 0, 1, …, m) имеет вид:
n
n 2
n
n
n
0 ( xi ) a0 1 ( xi ) 0 ( xi ) a1 2 ( xi ) 0 ( xi ) a2 ... m ( xi ) 0 ( xi ) am yi 0 ( xi );
i 0
i 0
i 0
i 0
i 0
n
n
n 2 n
n
1 ( xi ) a1 2 ( xi ) 1 ( xi ) a2 ... m ( xi ) 1 ( xi ) am yi 1 ( xi );
1 ( xi ) 0 ( xi ) a0
i 0
i 0
i 0
i 0
i 0
n
n
n
n 2
n
2 ( xi ) a2 ... m ( xi ) 2 ( xi ) am yi 2 ( xi );
1 ( xi ) 0 ( xi ) a0 2 ( xi ) 1 ( xi ) a1
i 0
i 0
i 0
i 0
i 0
......................................................................................................
n
n
n
n 2
n
m ( xi ) am yi m ( xi ).
m ( xi ) 0 ( xi ) a0 m ( xi ) 1 ( xi ) a1 m ( xi ) 2 ( xi ) a2 ...
i 0
i 0
i 0
i 0
i 0
14
15. Метод наименьших квадратов
Например, пусть m = 2k + 1 иQ( x, a0 , a1 , b1 , a2 , b2 , , ak , bk ) a0 a j cos jx b j sin jx .
Тогда СЛАУ примет вид
k
j 1
k
k
n
n
n
(n 1)a0 a j cos jxi
b j sin jxi
yi ;
j 1
j 1
i 0
i 0
i 0
k
n
n
k n
n
cos pxi a0 a j (cos jxi cos pxi ) b j (sin jxi cos pxi ( yi cos pxi );
j 1
i 0
j 1 i 0
i 0
i 0
n
k
n
k n
n
sin pxi a0 a j (cos jxi sin pxi ) b j (sin jxi sin pxi ) ( yi sin pxi );
i 0
j 1
i 0
j 1 i 0
i 0
p 1, 2, , k
15
16. Метод наименьших квадратов
В частном случае при k = 2 получим СЛАУn
n
n
n
n
(n 1)a0
cos xi a1
cos 2 xi a2
sin xi b1
sin 2 xi b2 yi ;
i 0
i 0
i 0
i 0
i 0
n
n
n
n
n
n
2
cos xi a1 cos 2 xi cos xi a2 sin xi cos xi b1 sin 2 xi cos xi b2 yi cos xi ;
cos xi a0
i 0
i 0
i 0
i 0
i 0
i 0
n
n
n
n
n
n
2
cos 2 xi a2 sin xi cos 2 xi b1 sin 2 xi cos 2 xi b2 yi cos 2 xi ;
cos 2 xi a0 cos xi cos 2 x i a1
i 0
i 0
i 0
i 0
i 0
i 0
n
n
n
n
n
n
2
sin xi a0 cos xi sin x i a1 cos 2 xi sin xi a2
sin xi b1 sin 2 xi sin xi b2 yi sin xi ;
i 0
i 0
i 0
i 0
i 0
i 0
n
n
n
n
n
n
2
sin 2 x a cos x sin 2 x a cos 2 x sin 2 x a sin x sin 2 x b
sin 2 xi b2 yi sin 2 xi ;
i
0
i
i
1
i
i
2
i
i 1
i 0
i 0
i 0
i 0
i 0
i 0
16
17. Тема 3.2 Интерполяция
Обобщенная постановка задачи интерполяции:Дано:
значения функции y = f(x), x [a, b]:
yi = f(xi), i = 0, 1, 2, …, n (xi [a, b]).
Найти:
функцию y = g(x) такую, что
g(xi) = yi, i = 0, 1, 2, …, n.
17
18. Тема 3.2 Интерполяция Геометрический смысл:
yy2
y = g(x)
y0
y5
y4
x0 O
y3
y1
x1
x2
x3
x4
y = f(x)
x5
x
18
19. Тема 3.2 Интерполяция
Задача интерполяции обобщенным многочленом:Пусть задана система функций:
φ0(x), φ1(x), φ2(x), ..., φn(x).
Обобщенным многочленом называется функция
n
n(x) = a0φ0(x)+a1φ1(x)+a2φ2(x)+...+anφn(x) = a j j ( x),
j 1
такая, что
n(xi) = yi, i = 0, 1, 2, …, n.
19
20. Тема 3.2 Интерполяция
Коэффициенты aj (j = 0, 1, 2, …, n) находятся из условия:a0 0 ( x0 ) a1 1 ( x0 ) a2 2 ( x0 ) ... an n ( x0 ) y0 ,
a ( x ) a ( x ) a ( x ) ... a ( x ) y ,
1 1 1
2 2 1
n n 1
1
0 0 1
a0 0 ( x2 ) a1 1 ( x2 ) a2 2 ( x2 ) ... an n ( x2 ) y2 , – СЛАУ.
.....................................................................................
a0 0 ( xn ) a1 1 ( xn ) a2 2 ( xn ) ... an n ( xn ) yn ;
Для решения СЛАУ необходимо, чтобы для любых xi (i = 0, 1, 2, …, n), xi x j ,
i j
0 ( x0 ) 1 ( x0 ) ... n ( x0 )
0 ( x1 ) 1 ( x1 ) ... n ( x1 )
(1)
...
...
...
...
0 ( xn ) 1 ( xn ) ... n ( xn )
0,
система функций {φj(x)}j=0,1,...,n , удовлетворяющая условию (1), называется
20
чебышевской системой функций.
21. Тема 3.2 Интерполяция
Задача полиномиальной интерполяции:Пусть задана система функций вида:
φ0(x) = 1, φ1(x) = x, φ2(x) = x2, ..., φn(x) = xn.
Интерполяционным многочленом (полиномом)
называется функция
n
j
2
n
a
x
Pn(x) = a0x + a1x + a2 x + ... +an x = j ,
j 0
такая, что
Pn(xi) = yi, i = 0, 1, 2, …, n.
21
22. Тема 3.2 Интерполяция
ТеоремаСистема функций {1, x, x2, ..., xn} является чебышевской.
Доказательство:
1
1
1
...
1
x0
x1
x2
...
xn
x02
x12
x22
...
xn2
...
...
...
...
...
x0n
x1n
n
n
x2 ( xi x j ) 0 – определитель Вандермонда.
0 j i n
...
xnn
22
23. Тема 3.2.1 Интерполяционный многочлен (полином) Лагранжа
Интерполяционный многочлен (полином) Лагранжаимеет следующий вид:
Ln ( x) y0 Pn0 ( x) y1 Pn1 ( x) y2 Pn2 ( x) ... yn Pnn ( x),
где многочлен степени n такой, что
1, i j,
j
Pn ( xi )
0, i j.
Многочлен Pni ( x) Ci ( x x0 )( x x1 )...(x xi 1 )( x xi 1 )...(x xn ),
Pni ( xi ) 1 Ci
Pni ( x)
1
( xi x0 )( xi x1 )...(xi xi 1 )( xi xi 1 )...(xi xn )
n (x x )
( x x0 )( x x1 )...(x xi 1 )( x xi 1 )...(x xn )
j
.
( xi x0 )( xi x1 )...(xi xi 1 )( xi xi 1 )...(xi xn ) j 0, ( xi x j ) 23
j i
24. Тема 3.2.1 Интерполяционный многочлен (полином) Лагранжа
Интерполяционный многочлен (полином) ЛагранжаОбщая формула:
n
n
n
Ln ( x)
i 0
yi Pni ( x)
(x x j )
yi ( x x ) .
i 0
j 0 ,
j i
i
j
Частные случаи:
x x0
x x1
y1
n = 1: L1 ( x) y0
x0 x1
n = 2: L2 ( x) y0
n = 3: L3 ( x) y0
x1 x0
( x x1 )( x x2 )
( x x0 )( x x2 )
( x x0 )( x x1 )
y1
y2
( x0 x1 )( x0 x2 )
( x1 x0 )( x1 x2 )
( x2 x0 )( x2 x1 )
( x x1)( x x2 )( x x3 )
( x x0 )( x x2 )( x x3 )
( x x0 )( x x1)( x x3 )
( x x0 )( x x1)( x x2 )
y1
y2
y3
.
( x0 x1)( x0 x2 )( x0 x3 ) ( x1 x0 )( x1 x2 )( x1 x3 ) ( x2 x0 )( x2 x1)( x2 x3 ) ( x3 x0 )( x3 x1)( x3 x2 )
24
25. 3.2.1 Интерполяционная формула Лагранжа
Блок-схема алгоритмаBegin
L:=0
for i:=0 to n do
P:=1
for j:=0 to i–1 do
P:=P*(~
x –x(j))/(x(i)–x(j))
for j:=i+1 to n do
P:=P*(~
x–x(j))/(x(i)–x(j))
L:=L+y(i)*P
25
End
26. Ввод исходных данных в программу на языке Pascal
constn = 10;
a = 0;
b = 1;
var
x[n], y[n], L, P, h: double;
i, j: integer;
function f(x: double): double;
begin
f := sqrt(x);
end;
begin
h := (b–a)/n;
x[0] := a;
for i:=1 to n do
x[i] := x[i–1] + h;
for i:=0 to n do
y[i] := f(x[i]);
...
end.
26
27. 3.2.2 Интерполяционный полином Ньютона
Общий вид:первая формула Ньютона:
Pn(1) ( x) a0 a1 ( x x0 ) a 2 ( x x0 )( x x1 ) ... a n ( x x0 )( x x1 )...( x x n 1 )
вторая формула Ньютона:
Pn( 2) ( x) b0 b1 ( x x n ) b2 ( x x n )( x x n 1 ) ... bn ( x x n )( x x n 1 )...( x x1 )
27
28. 3.2.2 Полином Ньютона для равноотстоящих узлов интерполяции (xi+1–xi=h≡const)
Конечные разности:yi = yi+1–yi – конечные разности первого порядка;
2yi = yi+1– yi – конечные разности второго порядка;
3yi = 2yi+1– 2yi – конечные разности третьего порядка;
...
nyi = n-1yi+1– n-1yi – конечные разности n-го порядка;
28
29. 3.2.2 Полином Ньютона для равноотстоящих узлов интерполяции (xi+1–xi=h≡const)
Конечные разности:yi = yi+1–yi – конечные разности первого порядка;
2yi = yi+1– yi – конечные разности второго порядка;
3yi = 2yi+1– 2yi – конечные разности третьего порядка;
...
nyi = n-1yi+1– n-1yi – конечные разности n-го порядка;
29
30. 3.2.2 Полином Ньютона для равноотстоящих узлов интерполяции (xi+1–xi=h≡const)
Таблица конечных разностей:i
yi
yi
2 yi
3 yi
4 yi
5 yi
0
y0
y0
2y0
3y0
4y0
5y0
1
y1
y1
2y1
3y1
4y1
2
y2
y2
2y2
3y2
3
y3
y3
2y3
4
y4
y4
5
y5
30
31. 3.2.2 1-я формула Ньютона для равноотстоящих узлов интерполяции (xi+1–xi=h≡const)
Условия на аi:Pn(1) ( x0 ) y 0 ,
a0 y 0 ,
Pn(1) ( x1 ) y1 ,
a0 a1 h y1 ,
Pn(1) ( x 2 ) y 2 , a0 2a1 h 2a 2 h 2 y 2 ,
...
...
Pn(1) ( x n ) y n ;
a0 na1 h n(n 1)a 2 h 2 ... n!a n h n y n .
31
32. 3.2.2 1-я формула Ньютона для равноотстоящих узлов интерполяции (xi+1–xi=h≡const)
a0 y0 ,y1 y 0 y 0
a1
,
h
h
y 2 2 y1 y 0 y1
a 0 2a1 h 2a 2 h
2,
2
2h
2h
...
2
Общая формула аi:
k y 0
ak
, k 0,1,..., n
k
k! h
32
33. 3.2.2 2-я формула Ньютона для равноотстоящих узлов интерполяции (xi+1–xi=h≡const)
Общая формула:y 0
2 y 0
n y 0
P ( x) y 0
( x x0 )
( x x0 )( x x1 ) ...
( x x0 )( x x1 )...( x xn 1 )
2
n
h
2!h
n!h
(1)
n
Для программной реализации:
Pn(1) ( x) y 0 y 0
( x x0 )
( x x0 ) ( x x1 )
( x x0 ) ( x x1 ) ( x x 2 )
2 y 0
3 y 0
...
h
h 2
h
h
2h
3h
c1
n y 0
c2
c3
( x x0 ) ( x x1 ) ( x x n 1 )
...
.
h
2h nh
cn
( x x0 )
c1
,
h
( x xk )
c k 1 c k
, k 1,..., n 1
(k 1)h
33
34. 2-я формула Ньютона для равноотстоящих узлов интерполяции (xi+1–xi=h≡const)
Условия на bi:Pn( 2 ) ( x n ) y n ,
b0 y n ,
Pn( 2 ) ( x n 1 ) y n 1 ,
b0 b1 h y n 1 ,
Pn( 2 ) ( x n 2 ) y n 2 , b0 2b1 h 2b2 h 2 y n 2 ,
...
...
Pn( 2 ) ( x0 ) y 0 ;
b0 nb1 h n(n 1)b2 h 2 ... ( 1) n n!bn h n y 0 .
34
35. 2-я формула Ньютона для равноотстоящих узлов интерполяции (xi+1–xi=h≡const)
b0 y n ,y n y n 1 y n 1
b1
,
h
h
y n 2 y n 1 y n 2 y n 2
2
b0 2b1 h 2a 2 h
,
2
2
2h
2h
...
Общая формула bi:
k y n k
bk
, k 0,1,..., n
k
k! h
35
36. 1-я формула Ньютона для равноотстоящих узлов интерполяции (xi+1–xi=h≡const)
Общая формула:y n 1
2 y n 2
n y 0
P ( x) y n
( x xn )
( x xn )( x xn 1 ) ...
( x x n )( x xn 1 )...( x x1 )
2
n
h
2!h
n!h
( 2)
n
Для программной реализации:
Pn( 2) ( x) y n y n 1
( x xn )
( x x n ) ( x x n 1 )
( x x n ) ( x x n 1 ) ( x x n 2 )
2 y n 1
3 y n 2
...
h
h
2
h
h
2
h
3
h
c1
n y 0
c2
c3
( x x n ) ( x x n 1 ) ( x x1 )
...
.
h
2
h
nh
cn
( x xn )
c1
,
h
( x xn k )
c k 1 c k
, k 1,..., n 1
(k 1)h
36
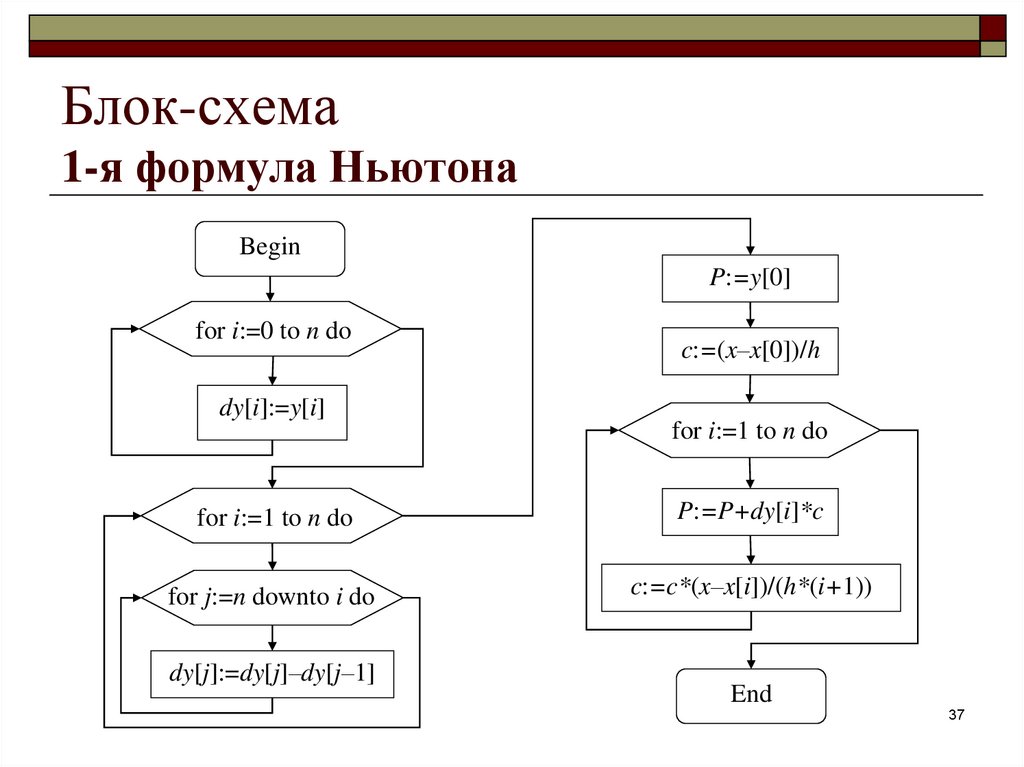
37. Блок-схема 1-я формула Ньютона
BeginP:=y[0]
for i:=0 to n do
dy[i]:=y[i]
c:=(x–x[0])/h
for i:=1 to n do
for i:=1 to n do
P:=P+dy[i]*c
for j:=n downto i do
c:=c*(x–x[i])/(h*(i+1))
dy[j]:=dy[j]–dy[j–1]
End
37
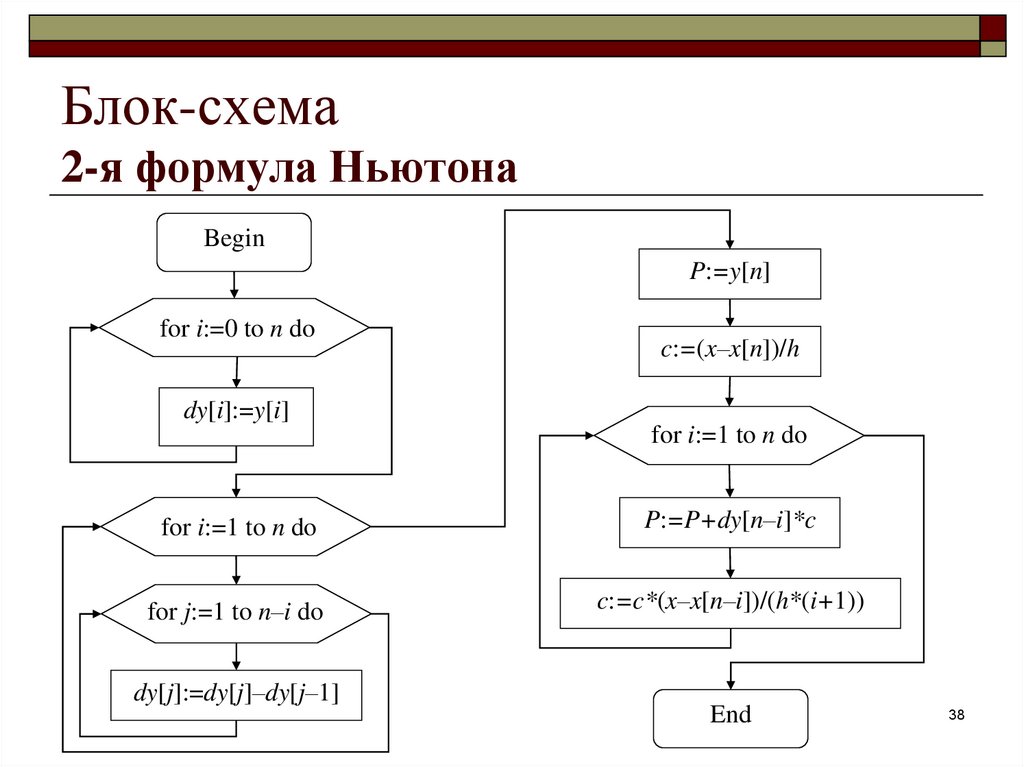
38. Блок-схема 2-я формула Ньютона
BeginP:=y[n]
for i:=0 to n do
c:=(x–x[n])/h
dy[i]:=y[i]
for i:=1 to n do
for i:=1 to n do
P:=P+dy[n–i]*c
for j:=1 to n–i do
c:=c*(x–x[n–i])/(h*(i+1))
dy[j]:=dy[j]–dy[j–1]
End
38
39. Полином Ньютона для неравноотстоящих узлов интерполяции (xi+1–xi=h ≠ const)
Разделенные разности:xi , xi 1 yi 1 yi
xi 1 xi
– разделенные разности первого порядка;
xi , xi 1 , xi 2 xi 1 , xi 2 xi , xi 1 – разделенные разности второго порядка;
xi 2 xi
xi , xi 1 , xi 2 , xi 3 xi 1 , xi 2 , xi 3 xi , xi 1 , xi 2 – разделенные разности третьего порядка;
xi 3 xi
...
xi , xi 1 ,..., xi n xi 1 ,..., xi n xi ,..., xi n 1 – разделенные разности n-го порядка.
xi n xi
39
40. Полином Ньютона для неравноотстоящих узлов интерполяции (xi+1–xi=h ≠ const)
Таблица разделенных разностей:i
xi
yi [xi, xi+1] [xi, xi+1, xi+2] [xi, xi+1, xi+2, xi+3] [xi, xi+1, xi+2, xi+3 , xi+4]
0 x0 y0 [x0, x1]
[x0, x1, x2] [x0, x1, x2, x3]
1 x1 y1 [x1, x2]
[x1, x2, x3] [x1, x2, x3 , x4]
2 x2 y2 [x2, x3]
[x2, x3, x4]
[x0, x1, x2, x3 , x4]
3 x3 y3 [x3, x4]
4 x4 y4
40
41. Погрешность полиномиальной интерполяции
Теорема:M n 1 ~
f (~
x ) Pn ( ~
x)
( x x0 )( ~
x x1 )...( ~
x xn ) ,
(n 1)!
M n 1 max f ( n 1) ( x)
x [ x0 , xn ]
42. Полином Ньютона для неравноотстоящих узлов интерполяции (xi+1–xi=h ≠ const)
Общий вид:первая формула Ньютона:
Pn(1) ( x) y0 [ x0 , x1 ]( x x0 ) [ x0 , x1 , x2 ]( x x0 )( x x1 ) ...
[ x0 , x1 ,..., xn ]( x x0 )( x x1 )...( x xn 1 );
вторая формула Ньютона:
Pn( 2) ( x) yn [ xn 1 , xn ]( x xn ) [ xn 2 , xn 1 , xn ]( x xn )( x xn 1 ) ...
[ x0 , x1 ,..., xn ]( x xn )( x xn 1 )...( x x1 ).
42
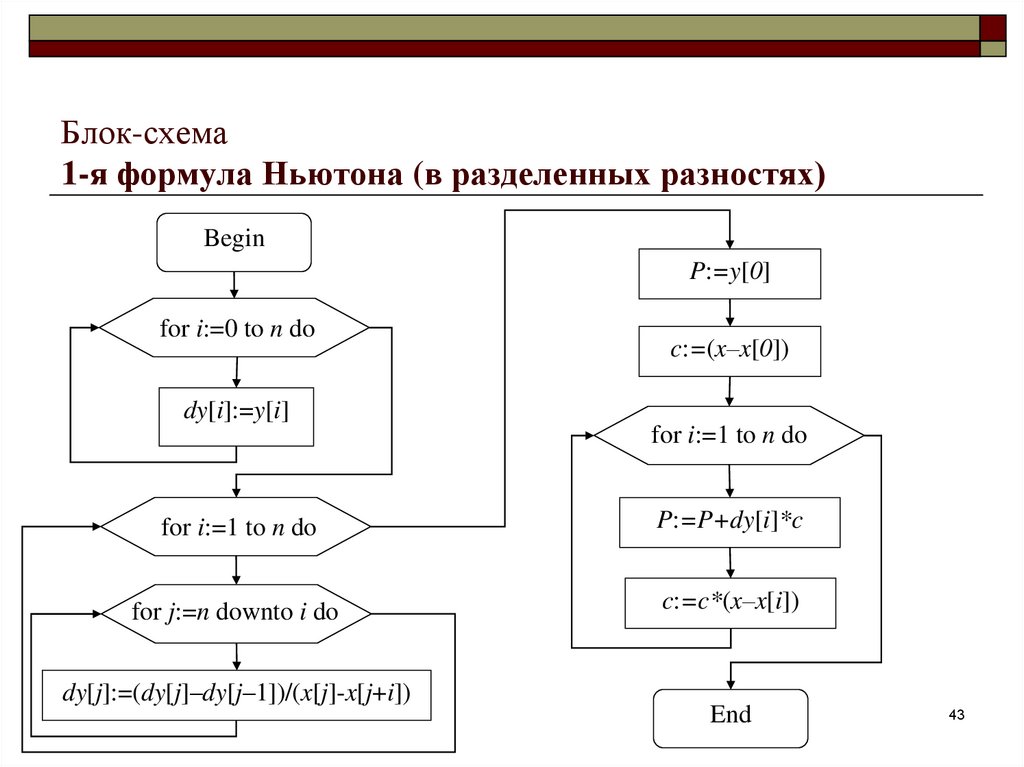
43. Блок-схема 1-я формула Ньютона (в разделенных разностях)
BeginP:=y[0]
for i:=0 to n do
c:=(x–x[0])
dy[i]:=y[i]
for i:=1 to n do
for i:=1 to n do
P:=P+dy[i]*c
for j:=n downto i do
c:=c*(x–x[i])
dy[j]:=(dy[j]–dy[j–1])/(x[j]-x[j+i])
End
43
44. Блок-схема 2-я формула Ньютона (в разделенных разностях)
BeginP:=y[n]
for i:=0 to n do
c:=(x–x[n])
dy[i]:=y[i]
for i:=1 to n do
for i:=1 to n do
P:=P+dy[n–i]*c
for j:=1 to n–i do
c:=c*(x–x[n–i])
dy[j]:=(dy[j]–dy[j–1])/(x[j]-x[j+i])
End
44







































 mathematics
mathematics








