Конечные разности. Первая и вторая интерполяционные формулы Ньютона. Погрешности интерполяции. (Лекция 4)

1. Лекция 4

1. Конечные разности
2. Первая интерполяционная формула
Ньютона
3. Вторая интерполяционная формула
Ньютона
4. Погрешности интерполяции

2. Конечные разности 1–го порядка

Если интерполируемая функция y = f(x) задана в
равноотстоящих узлах, так что xi = x0 + i∙h, где h – шаг таблицы, а
i = 0, 1, … n, то для интерполяции могут применяться формулы
Ньютона, использующие конечные разности.
Конечной разностью первого порядка называется разность yi
= yi+1 - yi, где
yi+1= f(xi+h) и yi = f(xi). Для функции, заданной
таблично в (n+1) узлах, i = 0, 1, 2, …, n, конечные разности
первого порядка могут быть вычислены в точках 0, 1, 2,…, n - 1:
y 0 y1 y 0 ,
y1 y 2 y1,
.......................
yn 1 yn yn 1.

3. Конечные разности высших порядков

Используя конечные разности первого порядка, можно
получить конечные разности второго порядка 2yi = yi+1 - yi:
2 y 0 y1 y 0 ;
2 y1 y 2 y1;
..........................
2 y n 2 y n 1 y n 2 .
Конечные разности k-го порядка в узле с номером i могут
быть вычислены через разности (k-1)–го порядка:
k yi k 1yi 1 k 1yi
Любые конечные разности можно вычислить через значения
функции в узлах интерполяции, например:
2 y 0 y1 y 0 (y 2 y1 ) (y1 y 0 ) y 2 2y1 y 0 .

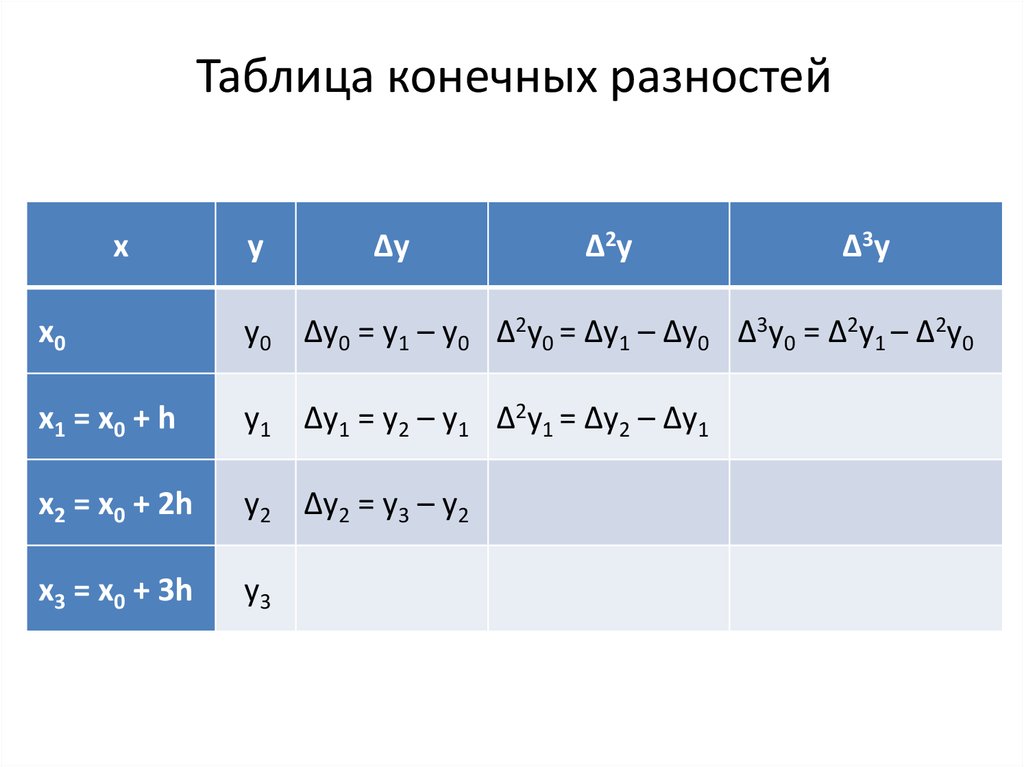
4. Таблица конечных разностей

x
y
Δy
Δ2y
Δ3y
x0
y0 Δy0 = y1 – y0 Δ2y0 = Δy1 – Δy0 Δ3y0 = Δ2y1 – Δ2y0
x1 = x0 + h
y1 Δy1 = y2 – y1 Δ2y1 = Δy2 – Δy1
x2 = x0 + 2h
y2 Δy2 = y3 – y2
x3 = x0 + 3h
y3

5. Конечные разности и степень многочлена

По величине конечных разностей можно
сделать
вывод
о
степени
интерполяционного
многочлена,
описывающего
таблично
заданную
функцию.
Если
для
таблицы
с
равноотстоящими
узлами
конечные
разности k-го порядка постоянны или
соизмеримы с заданной погрешностью, то
функцию можно представить многочленом
k-й степени.

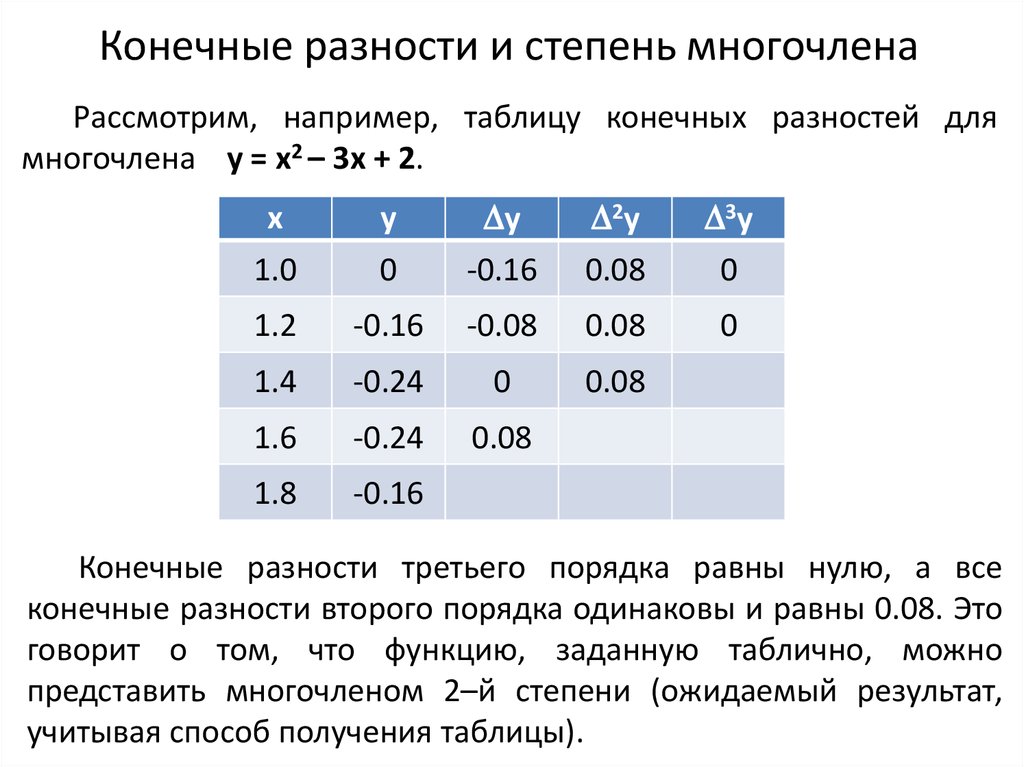
6. Конечные разности и степень многочлена

Рассмотрим, например, таблицу конечных разностей для
многочлена y = x2 – 3x + 2.
0
y
-0.16
2y
0.08
3y
0
1.2
-0.16
-0.08
0.08
0
1.4
-0.24
0
0.08
1.6
-0.24
0.08
1.8
-0.16
x
y
1.0
Конечные разности третьего порядка равны нулю, а все
конечные разности второго порядка одинаковы и равны 0.08. Это
говорит о том, что функцию, заданную таблично, можно
представить многочленом 2–й степени (ожидаемый результат,
учитывая способ получения таблицы).

7. Первая интерполяционная формула Ньютона

Пусть функция y = f(x) задана в n+1 равноотстоящих узлах xi , i = 0, 1,
2,…n с шагом h. Требуется найти интерполяционный многочлен Pn(x)
степени n, удовлетворяющий условию:
Pn(xi) = yi, i =0, 1, 2, …,n .
Будем искать интерполяционный многочлен в виде:
Pn(x) = a0 + a1(x-x0) + a2(x-x0)(x-x1) + … + an(x-x0)(x-x1)…(x-xn-1),
где аi, i = 0, 1, 2,…n – неизвестные коэффициенты, не зависящие от узлов
интерполяции. Найдем эти коэффициенты из условий интерполяции.
Пусть х = x0, тогда Pn(x0) = y0 = a0. Следовательно, a0 = y0.
Пусть х = x1, тогда Pn(x1) = y1 = a0 + a1(x1 - x0) = y0 + a1(x1 - x0), откуда
a1
y1 y0 y0
.
x1 x0
h
Теперь пусть х = х2 , тогда:
Pn (x 2 ) y 2 a0 a1(x 2 -x 0 ) a2 (x 2 -x 0 )(x 2 -x1) y 0
y 0
2h a2 2h2.
h
Выразив из этого выражения a2, получим:
y 2 2 y0 y0 y 2 2(y1 y0 ) y0 y 2 2y1 y 0 2 y 0
a2
.
2h2
2h2
2h2
2h2

8. Первая интерполяционная формула Ньютона

Продолжая подстановки, можно получить выражение для любого
коэффициента с номером i:
i y 0
ai
,
i! hi
i 0,1,...,n.
Подставив найденные значения коэффициентов в исходное выражение,
получим первую интерполяционную формулу Ньютона:
y0
2 y0
n y 0
Pn (x) y0
(x x0 )
(x x 0 )(x x1) ...
(x x 0 )...(x x n 1).
1!h
2!h2
n!hn
Из формулы видно, что в ней используется верхняя строка таблицы
конечных разностей (слайд 4). Особенностью формулы является также
последовательное увеличение степени многочлена по мере добавления
очередных слагаемых. Это позволяет уточнять получаемый результат без
пересчета уже учтенных слагаемых.

9. Первая интерполяционная формула Ньютона

Первая интерполяционная формула Ньютона может быть записана в
более компактном и удобном для программной реализации виде.
Обозначив
q
x x0
,
h
x x 0 qh
и проведя несложные преобразования вида:
x x1 x x 0 h
q 1;
h
h
x xn
x x2
q n 1,
q 2;.....;
h
h
получим первую интерполяционную формулу Ньютона, выраженную
относительно неизвестной q:
n y 0
2 y0
q(q 1)...(q n 1).
q(q 1) ...
Pn (x) Pn (x0 hq) y0 y0q
n!
2!

10. Первая интерполяционная формула Ньютона

Конечные разности высших порядков, используемые в формуле
Ньютона, имеют обычно большую погрешность, связанную с ошибками
округления при вычитании близких значений. Поэтому соответствующие
слагаемые формулы имеют также большую погрешность. Чтобы уменьшить
их вклад в сумму, то есть в конечный результат, надо, чтобы выполнялось
условие |q| < 1. Это обеспечивается, если точка интерполяции x находится
между двумя первыми узлами таблицы: x0 < x < x1. По этой причине
интерполяцию с использованием первой формулы Ньютона называют
интерполяцией в начале таблицы или интерполяцией вперед.
Для частных случаев линейной (n=1) и квадратичной (n=2)
интерполяции первая интерполяционная формула Ньютона принимает
следующий вид:
P1(x) y0 y0q.
P2 (x) y 0 y 0 q 2 y 0
q(q 1)
.
2

11. Пример использования первой интерполяционной формулы Ньютона

Пусть интерполируемая функция f(x) задана той же таблицей,
что и в примере на слайде 6. Требуется найти приближенное
значение функции в точке x = 1.1 путем квадратичной
интерполяции по первой формуле Ньютона.
x
1.0
1.2
1.4
1.6
1.8
y
0
-0.16
-0.24
-0.24
-0.16
y
-0.16
-0.08
0
0.08
2y 3y
0.08 0
0.08 0
0.08
Шаг таблицы h = 0.2
q = (x – x0)/h = 0.5
q(q 1)
2
0.5(0.5 1)
0 ( 0.16) 0.5 0.08
0.09
2
P2 (x) y 0 Δy 0 q Δ 2 y 0
Результат совпадает с
значением многочлена
y = x2 – 3x + 2, из которого
получена таблица

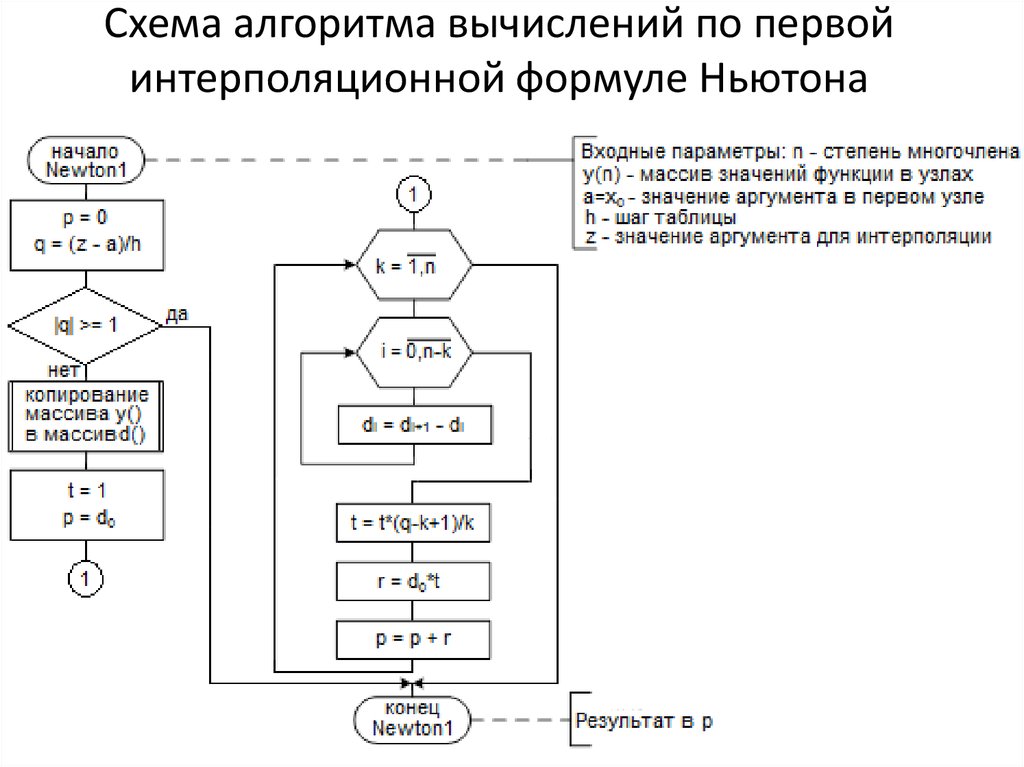
12. Схема алгоритма вычислений по первой интерполяционной формуле Ньютона

13. Вторая интерполяционная формула Ньютона

Вторая формула Ньютона обладает аналогичными свойствами
относительно правой части таблицы. Для ее построения используют
многочлен вида:
Pn(x) = a0 + a1(x-xn) + a2(x-xn)(x-xn-1) + … + an(x-xn)(x-xn-1)…(x-x1),
где аi, i = 0, 1, 2, … n – коэффициенты, не зависящие от узлов интерполяции.
Для определения коэффициентов аi будем в это выражение поочередно
подставлять узлы интерполяции. При х = xn Pn(xn) = yn, следовательно,
a0 = yn.
При х = xn-1 имеем Pn(xn-1) = yn-1 = a0 + a1(xn-1-xn) = yn + a1(xn-1-xn),
откуда
a1
yn 1 yn yn yn 1 yn 1
.
xn 1 xn xn xn 1
h

14. Вторая интерполяционная формула Ньютона

Продолжая подстановки, получим выражения для всех коэффициентов
многочлена и вторую интерполяционную формулу Ньютона:
n y 0
yn 1
2 yn 2
Pn (x) yn
(x xn )
(x xn )(x xn 1 )
(x xn )...(x x1 ).
2
n
1!h
2!h
n!h
Из формулы видно, что в ней используется нижняя диагональ таблицы
конечных разностей (слайд 4). Как и в первой формуле Ньютона, добавление
очередных слагаемых ведет к последовательное увеличению степени
многочлена, что позволяет уточнять получаемый результат без пересчета уже
учтенных слагаемых.
Введя обозначение: q
x xn
,
h
x xn hq
и, проделав несложные преобразования, получим вторую интерполяционную
формулу Ньютона, выраженную относительно переменной подстановки q:
n y 0
2 yn 2
Pn (x) yn yn 1q
q(q 1) ...
q(q 1)...(q n 1).
2!
n!

15. Вторая интерполяционная формула Ньютона

Из тех же соображений, что и в случае первой формулы Ньютона, для
уменьшения вычислительной погрешности надо, чтобы выполнялось условие
|q| < 1. Это обеспечивается, если точка интерполяции x находится между
двумя последними узлами таблицы: xn-1 < x < xn. По этой причине
интерполяцию с использованием второй формулы Ньютона называют
интерполяцией е конце таблицы или интерполяцией назад.
Для частных случаев линейной (n=1) и квадратичной (n=2)
интерполяции вторая интерполяционная формула Ньютона принимает
следующий вид:
P1 ( x) y n y n 1q
2 y n 2
P2 ( x) y n y n 1 q
q( q 1)
2!

16. Пример использования второй интерполяционной формулы Ньютона

Пусть интерполируемая функция f(x) задана той же таблицей,
что и в примере на слайде 11. Требуется найти приближенное
значение функции в точке x = 1.7 путем квадратичной
интерполяции по второй формуле Ньютона.
x
1.0
1.2
1.4
1.6
1.8
y
0
-0.16
-0.24
-0.24
-0.16
y
-0.16
-0.08
0
0.08
2y 3y
0.08 0
0.08 0
0.08
Шаг таблицы h = 0.2
q = (x – xn)/h = -0.5
Результат совпадает с
значением многочлена
y = x2 – 3x + 2, из
которого получена
таблица
q(q 1)
2
0.5( 0.5 1)
0.16 0.08 ( 0.5) 0.08
0.21
2
P2 (x) y n Δy n 1 q Δ 2 y n 2

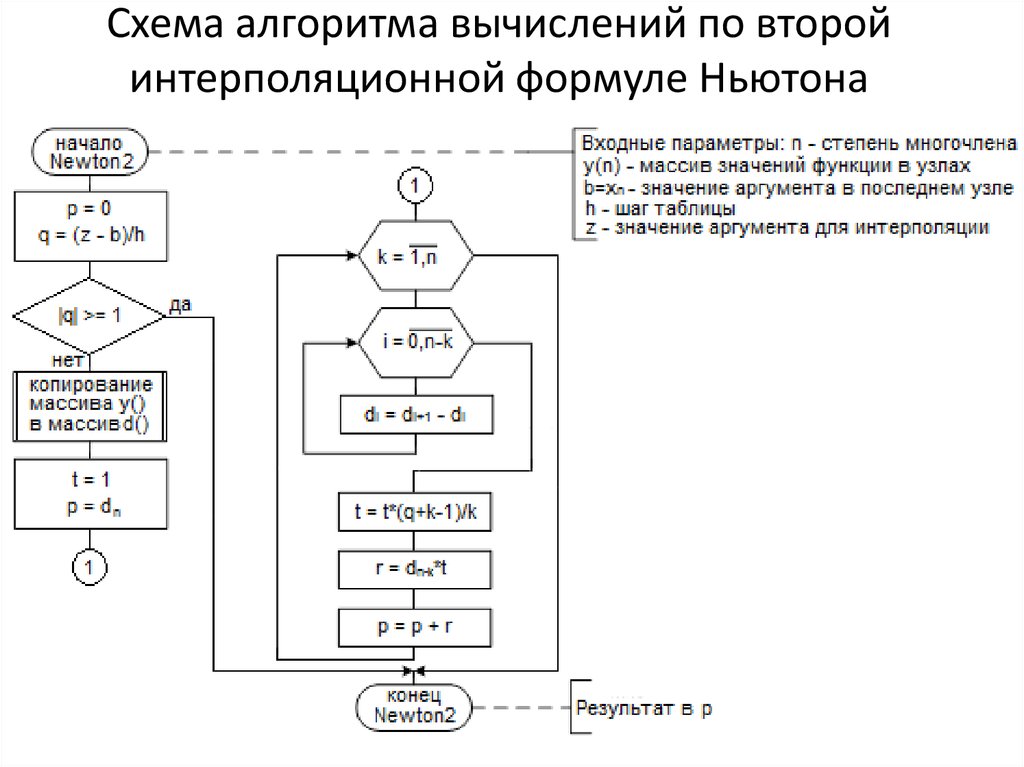
17. Схема алгоритма вычислений по второй интерполяционной формуле Ньютона

18. Погрешности интерполяции

Интерполирующая функция в точках между
узлами интерполяции заменяет интерполирующую
функцию приближенно:
f(x) = F(x) + R(x), где R(x) – погрешность
интерполяции.
Для оценки погрешности необходимо иметь
необходимо иметь определенную информацию об
интерполируемой функции f(x). Предположим, что
f(x) определена на отрезке [a;b], содержащем все
узлы xi, и при x, принадлежащем [a;b], имеет все
производные f'(x), f''(x), … f(n+1)(x) до (n+1)–го
порядка включительно.

19. Погрешности интерполяции

Тогда

20. Выбор узлов интерполяции по формуле Лагранжа

При фиксированной степени многочлена:
x*
x0
x1
x2
x3
x4
x5
x
При последовательном увеличении степени
многочлена
x*
x4
x2
x0
x1
x3
x5
x

21. Практическая оценка погрешности интерполяции по формуле Лагранжа

На практике оценка максимального значения производной (n+1)–го
порядка Mn+1 при использовании формулы Лагранжа редко бывает возможна,
и поэтому используют приближенную оценку погрешности
R n (x) f(x) Ln (x) Ln 1 (x) Ln (x) ,
где n число используемых узлов .
Из приведенной формулы следует, что для оценки погрешности
интерполяции многочленом Лагранжа n–й степени необходимо
дополнительно вычислить значение многочлена (n+1)–й степени. Если
допустимая погрешность интерполяции задана, то необходимо, добавляя все
новые узлы, увеличивать степень многочлена до тех пор, пока модуль
разности между двумя последними значениями многочлена |Ln+1(x)-Ln(x)| не
станет меньше заданного значения.

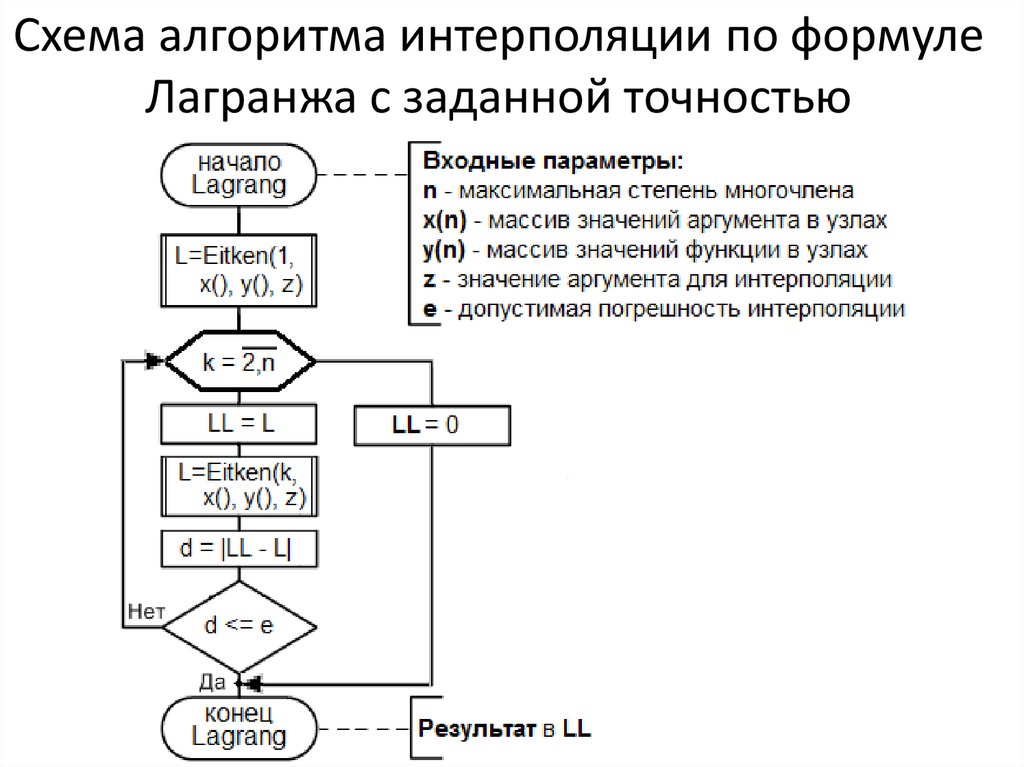
22. Схема алгоритма интерполяции по формуле Лагранжа с заданной точностью

23. Оценка погрешностей интерполяционных формул Ньютона

Для интерполяционных
приобретают следующий вид.
1–я формула Ньютона:
R n (x) h
n 1
формул
Ньютона
оценки
q(q 1) (q n) (n 1)
f
( )
(n 1)!
R n (x) h n 1
q(q 1) (q n)
M n 1
(n 1)!
2–я формула Ньютона:
R n (x) h
n 1
q(q 1) (q n) (n 1)
f
( )
(n 1)!
R n (x) h n 1
q(q 1) (q n)
M n 1
(n 1)!
погрешности

24. Практическая оценка погрешностей интерполяционных формул Ньютона

При использовании интерполяционных формул Ньютона величину
f(n+1)(ξ) можно приближенно оценивать по величинам конечных разностей:
f
(n 1)
n 1
Δ y0
( ) n 1
h
и в этом случае формулы для оценки погрешности приобретают следующий
вид:
1–я формула Ньютона:
R n (x)
q(q 1) (q n) n 1
Δ y0
(n 1)!
2–я формула Ньютона:
R n (x)
q(q 1) (q n) n 1
Δ y0
(n 1)!

25. Интерполяция по формулам Ньютона с заданной точностью

Сравнивая эти формулы с формулами
Ньютона, можно увидеть, что для оценки
погрешности при интерполяции многочленом
n–й степени надо взять дополнительный узел
и вычислить слагаемое (n+1)–й степени.
Если задана допустимая погрешность
интерполяции ε, то надо последовательно
добавлять новые узлы и, соответственно,
новые слагаемые, увеличивая степень
интерполяционного многочлена до тех пор,
пока очередное слагаемое не станет меньше ε.

26. Схема алгоритма интерполяции по 1–й формуле Ньютона с заданной точностью