Similar presentations:
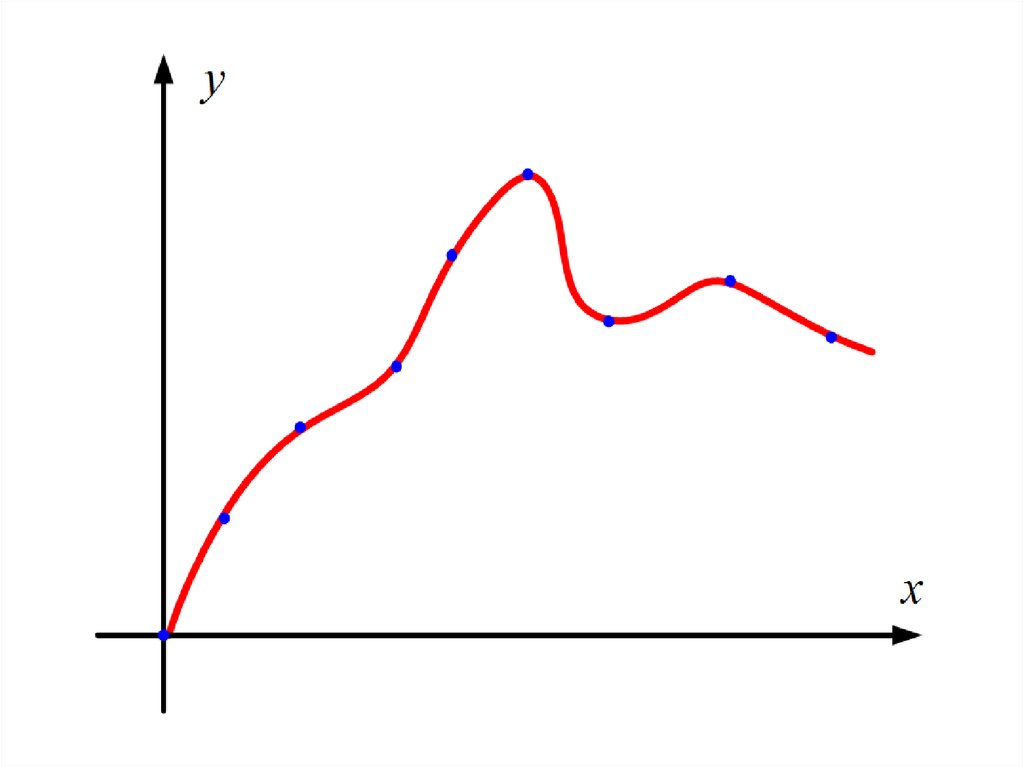
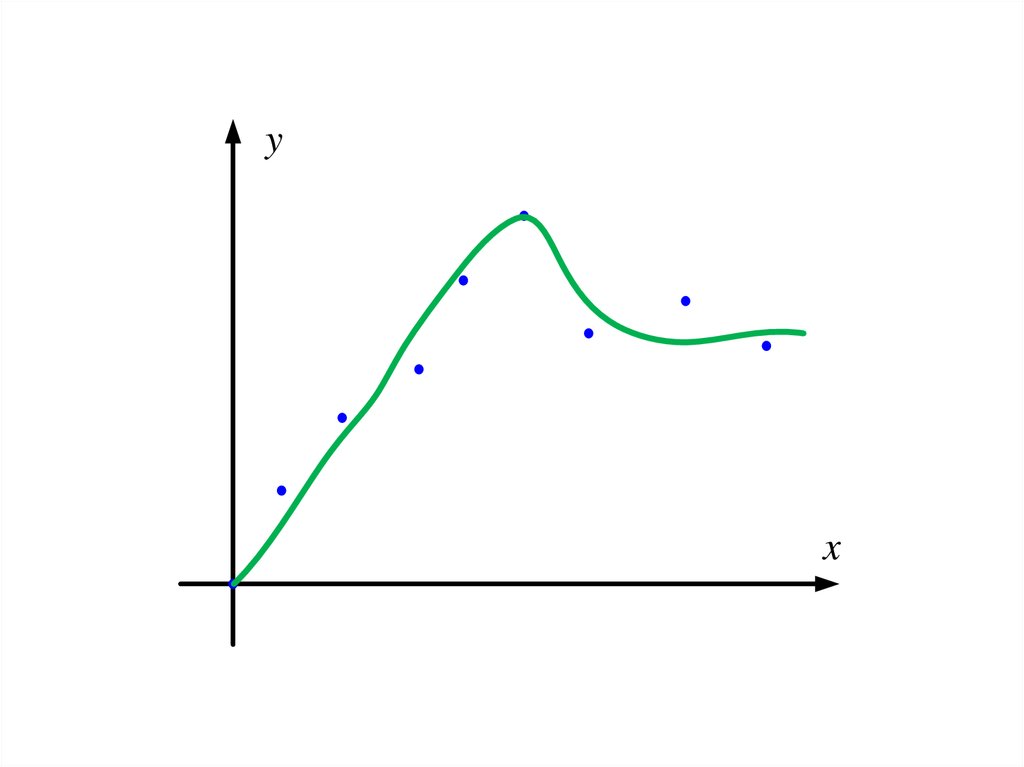
Интерполяция и экстраполяция
1. Интерполяция и экстраполяция
xy
x0
y0
xi
yi
xn
yn
2.
3.
yx
4.
5. Интерполяция и экстраполяция
xy
x0
y0
F ( x 0 ) y0
F ( x 1 ) y1
F ( x i ) yi
xi
yi
F ( x n ) yn
xn
yn
6.
• Задача интерполяцииF ( x) ?
x [ x0 ; xn ] x xi
• Задача экстраполяции
F ( x) ?
x [ x0 ; xn ]
7.
МЕТОДЫ ИНТЕРПОЛЯЦИИ• Для равноотстоящих точек
xi 1 xi const
xi 1 xi h
• Для не равноотстоящих точек
xi 1 xi const
8. Интерполяционные формулы для равноотстоящих точек
Fn ( x ) a0 a1 x a2 x2
an x
n
9. Конечные разности
yi yi 1 yiyi yi 1 yi
2
yi
n
n 1
yi 1
n 1
yi
10. Горизонтальная таблица конечных разностей
xy
y
2
y
3
y
4 y
x0
y0
y0
2
y0
3 y0
4 y0
x1
y1
y1
y1
3 y1
4 y1
xn
yn
2
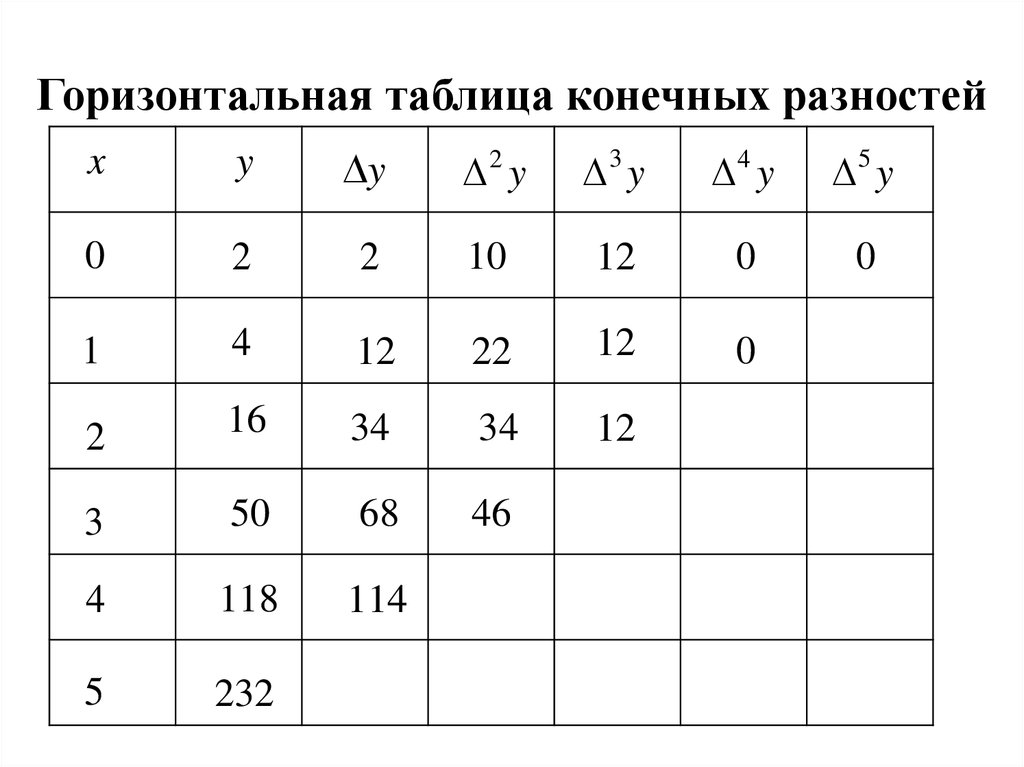
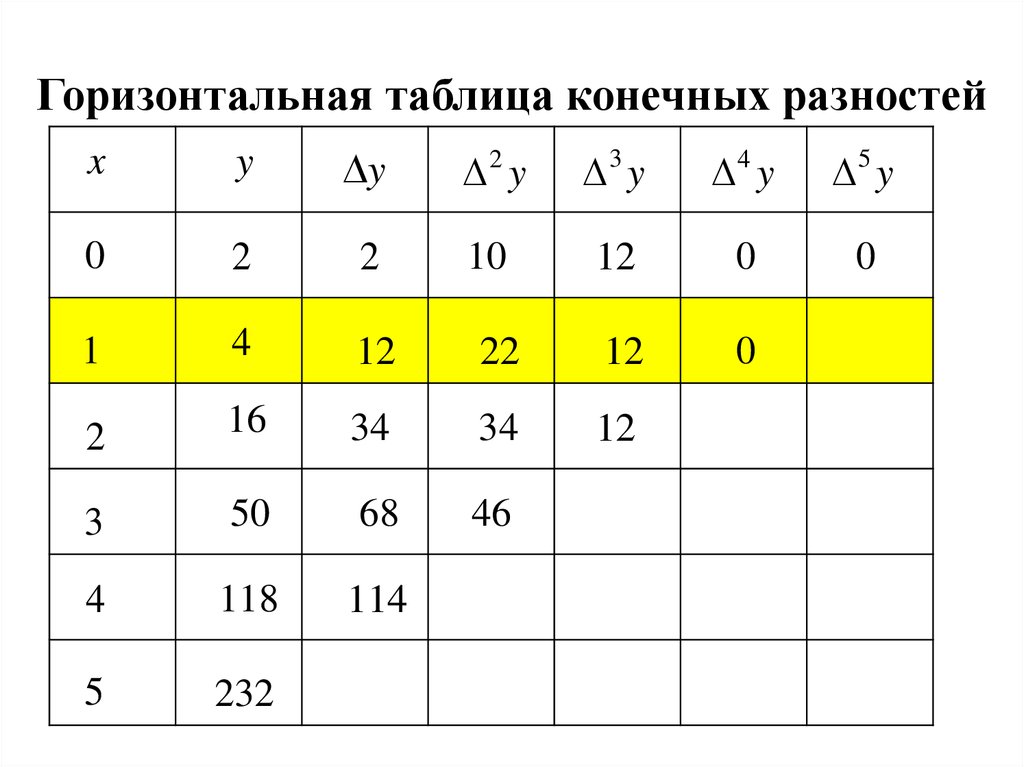
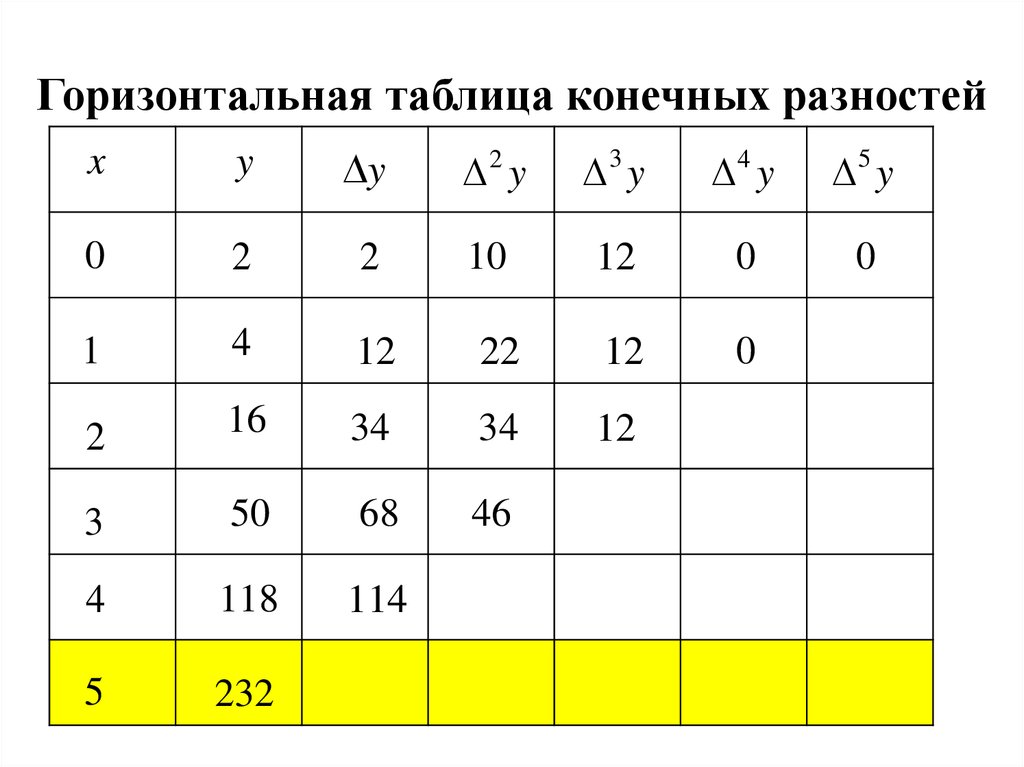
11. Горизонтальная таблица конечных разностей
xy
y
2 y
3 y
4 y
5 y
0
2
2
10
12
0
0
1
4
12
22
12
0
2
16
34
34
12
3
50
68
46
4
118
114
5
232
12. Первая интерполяционная формула Ньютона Общая формула
q( q 1) 2q( q 1)( q 2) 3
Pn ( x ) y0 q y0
y0
y0
2!
3!
q( q 1) ( q n 1) n
y0
n!
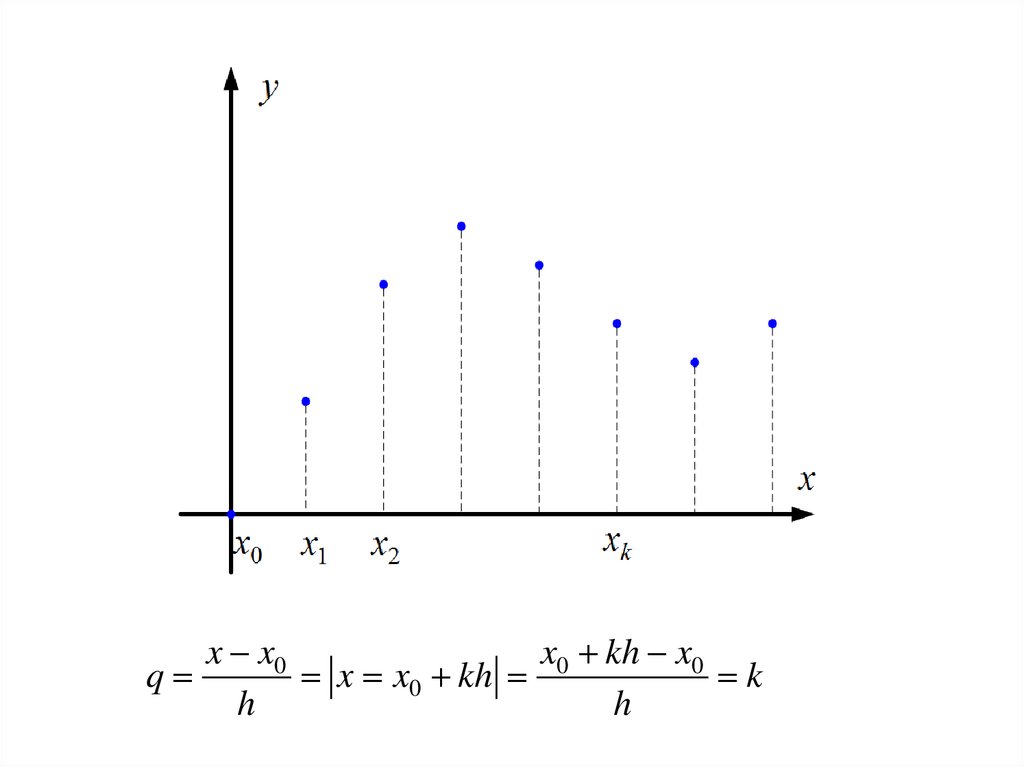
x x0
q
h
x x0
x x0 h x x1
q 1
1
h
h
h
x x2
q 2
h
13. Первая интерполяционная формула Ньютона Общая формула
(x x )( x x )( x x ) 2
0 y
0
1 y
P ( x) y
n
0
0
0
h
h 2 2!
( x x )( x x )( x x ) 3
0
1
2 y
0
3
h 3!
( x x )( x x ) ( x x
) n
0
1
n
1
y
0
n
h n!
14. Первая интерполяционная формула Ньютона Частный случай
q( q 1) 2q( q 1)( q 2) 3
Pn ( x ) y0 q y0
y0
y0
2!
3!
q( q 1) ( q n 1) n
y0
n!
x0 ближайшая узловая точка
y0 значение функции в ближайшей узловой точке
x x0
q
h
15.
x x0x0 kh x0
q
x x0 kh
k
h
h
16. Первая интерполяционная формула Ньютона. Частные случаи.
n 1x x0
P1 ( x ) y0 q y0 y0
y0
h
a0 a1 x
17. Первая интерполяционная формула Ньютона. Частные случаи.
n 2q( q 1) 2
P1 ( x ) y0 q y0
y0
2!
x x0
2 y0 ( x x0 ) ( x x0 )
y0
y 0
(
1)
h
2
h
h
y 0
2 y0
y0
( x x0 )
( x x0 )( x x0 h )
2
h
2h
y 0
2 y0
y0
( x x0 )
( x x0 )( x x1 )
2
h
2h
a0 a1 x a2 x 2
18. Горизонтальная таблица конечных разностей
xy
y
2 y
3 y
4 y
5 y
0
2
2
10
12
0
0
1
4
12
22
12
0
2
16
34
34
12
3
50
68
46
4
118
114
5
232
19.
x 0.7y ?
x0 1 y0 4
x x0 0.7 1
h 1 q
0.3
h
1
q( q 1) 2 q( q 1)( q 2) 3
P5 ( x ) y0 q y0
y 0
y 0
2!
3!
q( q 1)( q 2)( q 3) 4
y 0
4!
( 0.3)( 0.3 1)
( 0.3)( 0.3 1)( 0.3 2)
1 0.3 12
22
12
2
6
( 0.3)( 0.3 1)( 0.3 2)( 0.3 3)
0 2.896
24
20. Горизонтальная таблица конечных разностей
xy
y
2 y
3 y
4 y
5 y
0
2
2
10
12
0
0
1
4
12
22
12
0
2
16
34
34
12
3
50
68
46
4
118
114
5
232
21.
x 4.9y ?
x0 5
y0 232
x x0 4.9 5
h 1 q
0.1
h
1
P5 ( x ) y0 232
x 10 y ?
x0 5 y0 232
x x0 10 5
h 1 q
5
h
1
P5 ( x ) y0 232
22. Вторая интерполяционная формула Ньютона Общая формула
q( q 1) 2q( q 1)( q 2) 3
Pn ( x ) yn q yn 1
yn 2
yn 3
2!
3!
q( q 1) ( q n 1) n
y0
n!
x xn
q
h
x xn
x ( xn h ) x xn 1
q 1
1
h
h
h
x xn 2
q 2
h
23. Вторая интерполяционная формула Ньютона Общая формула
( x xn )( x xn )( x xn 1 ) 2
Pn ( x ) yn
yn 1
yn 2
2
h
h 2!
( x xn )( x xn 1 )( x xn 2 ) 3
yn 3
3
h 3!
( x xn )( x xn 1 )
n
h n!
( x x1 )
y0
n
24. Вторая интерполяционная формула Ньютона Частная задача
q( q 1) 2q( q 1)( q 2) 3
Pn ( x ) yn q yn 1
yn 2
yn 3
2!
3!
q( q 1) ( q n 1) n
y0
n!
xn ближайшая узловая точка
yn значение функции в ближайшей узловой точке
x xn
q
h
25. Горизонтальная таблица конечных разностей
xy
y
2 y
3 y
4 y
5 y
0
2
2
10
12
0
0
1
4
12
22
12
0
2
16
34
34
12
3
50
68
46
4
118
114
5
232
26.
x 4.9y ?
xn 5 yn 232
x xn 4.9 5
h 1 q
0.1
h
1
q( q 1) 2
q( q 1)( q 2) 3
P5 ( x ) yn q yn 1
y n 2
y n 3
2!
3!
q( q 1)( q 2)( q 3) n
q( q 1)( q 2)( q 3)( q 4) n
y n 4
y n 5
4!
5!
( 0.1)( 0.1 1)
( 0.1)( 0.1 1)( 0.1 2)
232 0.1 114
46
12
2
6
( 0.1)( 0.1 1)( 0.1 2)( 0.1 3)
0
24
( 0.1)( 0.1 1)( 0.1 2)( 0.1 3)( 0.1 4)
0 218.188
120
27. Интерполяционные формулы для не равноотстоящих точек
• Формула Лагранжа• Формула Ньютона для не равноотстоящих точек
28. Формула Лагранжа
( x x0 )( x x1 )...( x xi 1 )( x xi 1 )...( x xn )Ln ( xi ) yi
( xi x0 )( xi x1 )...( xi xi 1 )( xi xi 1 )...( xi xn )
i 0
n
i
x
y
0
1
2
3
0
1
2
5
2
3
12
147
29.
( x x1 )( x x2 )( x x3 )L3 ( xi ) y0
( x0 x1 )( x0 x2 )( x0 x3 )
( x x0 )( x x2 )( x x3 )
y1
( x1 x0 )( x1 x2 )( x1 x3 )
( x x0 )( x x1 )( x x3 )
y2
( x2 x0 )( x2 x1 )( x2 x3 )
( x x0 )( x x1 )( x x2 )
y3
( x3 x0 )( x3 x1 )( x1 x2 )
30.
( x 1)( x 2)( x 5)L3 ( xi ) 2
(0 1)(0 2)(0 5)
( x 0)( x 2)( x 5)
3
(1 0)(1 2)(1 5)
( x 0)( x 1)( x 5)
12
(2 0)(2 1)(2 5)
( x 0)( x 1)( x 2)
147
(5 0)(5 1)(5 2)
x x x 2
3
2
31. Погрешность интерполяционных формул
R n ( x ) f ( x ) Pn ( x )32. Погрешность первой интерполяционной формулы Ньютона
q( q 1)( q 2) ( q n ) n 1R n ( x)
y0
( n 1)!
33. Погрешность второй интерполяционной формулы Ньютона
q( q 1)( q 2) ( q n ) n 1R n ( x)
y0
(n 1)!
34. Погрешность первой и второй интерполяционных формул Ньютона при известном виде функции
R n ( x) hn 1
R n ( x) h
n 1
q( q 1)( q 2) ( q n ) ( n 1)
f
( )
(n 1)!
q( q 1)( q 2) ( q n ) ( n 1)
f
( )
(n 1)!
35. Пример
С какой точностью можно вычислить с помощьюинтерполяционной формулы ln100.5 для
рассматриваемого интервала [100; 103] с шагом h 1
q( q 1)( q 2)( q 3) (4)
R 3 ( x) h
f ( )
4!
4
f ( x ) ln x
1
1
(2)
f ( x)
f ( x) 2
x
x
2
6
(3)
(4)
f ( x) 3 f ( x) 4
x
x
(1)
36. Пример
0.3(0.3 1)(0.3 2)(0.3 3) 69
R 3 ( x) 1
2.41
10
4!
1004
4
37. Погрешность формулы Лагранжа
R n ( x)max f ( n 1) ( x )
x0 x xn
( n 1)!
( x x0 )( x x1 )
( x xn )
38. Выбор узлов интерполирования. Формула Чебышева
x0 xn xn x02i 1
xi
cos
2
2
2n 2






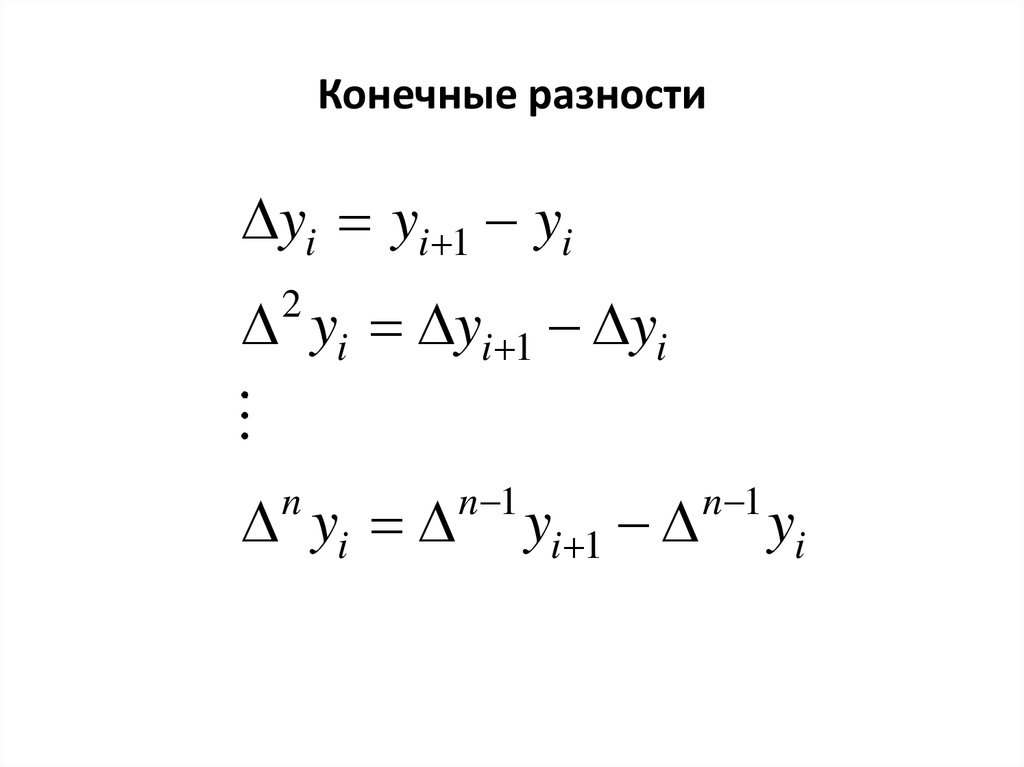















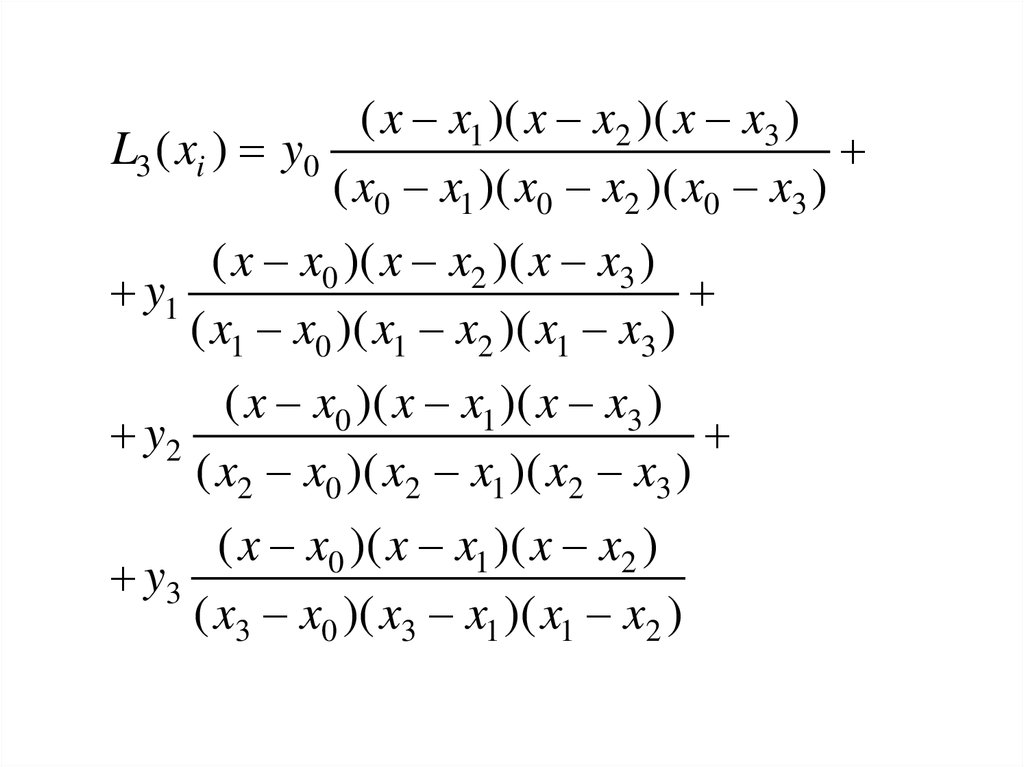
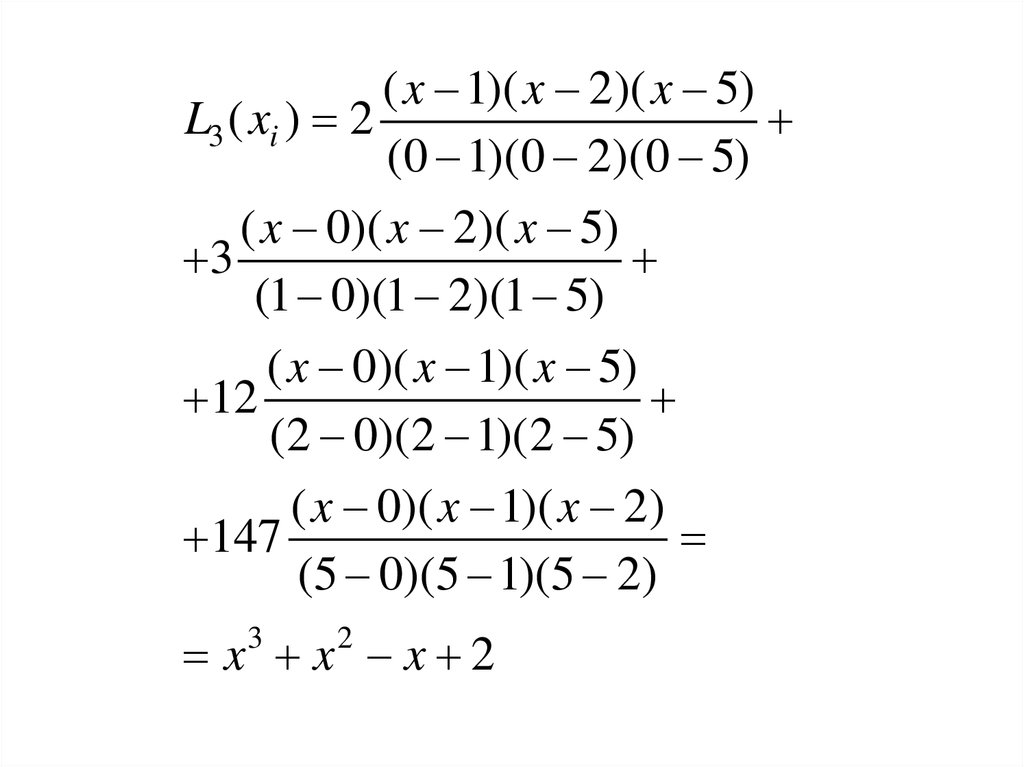








 mathematics
mathematics








