Similar presentations:
О некоторых особенностях использования численных методов приближения функций
1. О некоторых особенностях использования численных методов приближения функций
Янченко К.А.- АИМ103, Нигаматов Р.Ф.-АИМ101Руководитель: Лукманов Р.Л.
2. Задача интерполяции
Построить многочленLn x a0 a1 x a2 x 2 ...an x n
принимающий в заданных узлах заданные
значения:
Ln x f xi
i 0,1...n
(1)
Получается система линейных уравнений
относительно неизвестных коэффициентов
a0 , a1 , a2 ,...an
(2)
3. Интерполяционные многочлены Лагранжа и Ньютона
1. Интерполяционный многочлен Лагранжастроится в виде:
x xi
n
k i
c
x
,
где
i
Ln x ci x f xi
(x x )
i 0
k i
k
i
2. Интерполяционный многочлен Ньютона имеет
вид:
Ln x c0 c1 x x0 c2 x x0 x x1 ...cn x x0 x x1 ... x xn 1
Коэффициенты с0 , с1 , с2 ,...сn могут быть найдены
последовательно из условий интерполяции (2).
4. О погрешностях интерполяционных формул
M n 1x
f x Ln x
n 1 !
n 1
x , x П x x
n
где M n 1 sup f
Если f x достаточно гладкая, то погрешность
стремится к нулю с увеличением n:
x a ,b
i 0
i
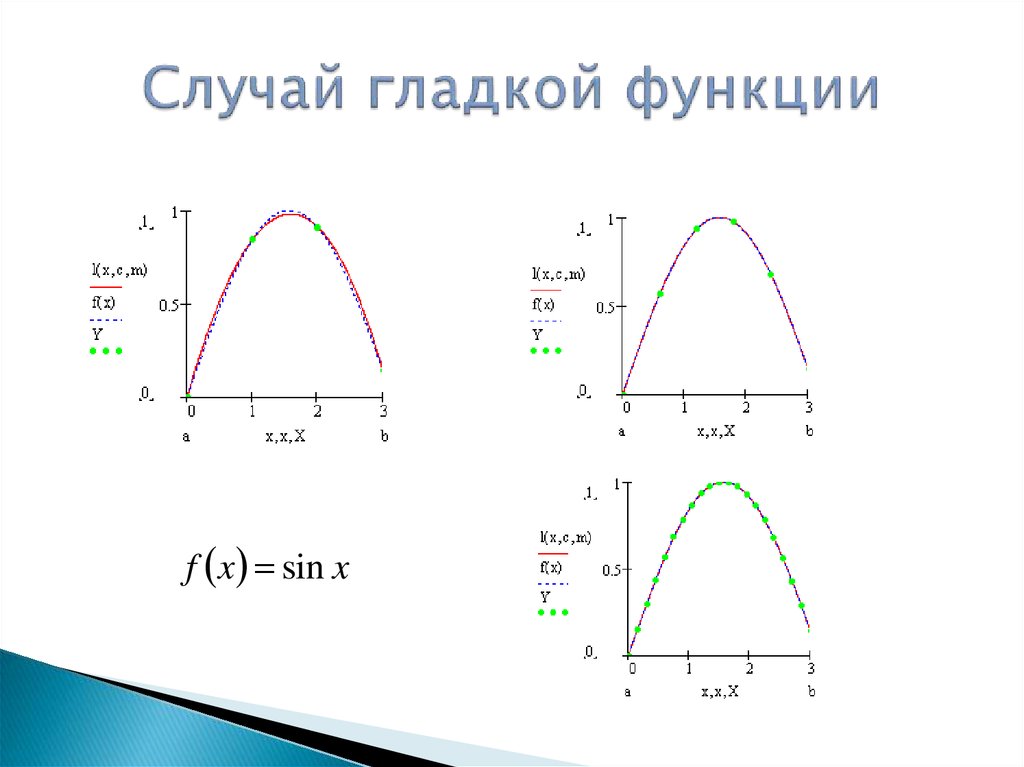
5. Случай гладкой функции
f x sin x6. Случай негладкой функции
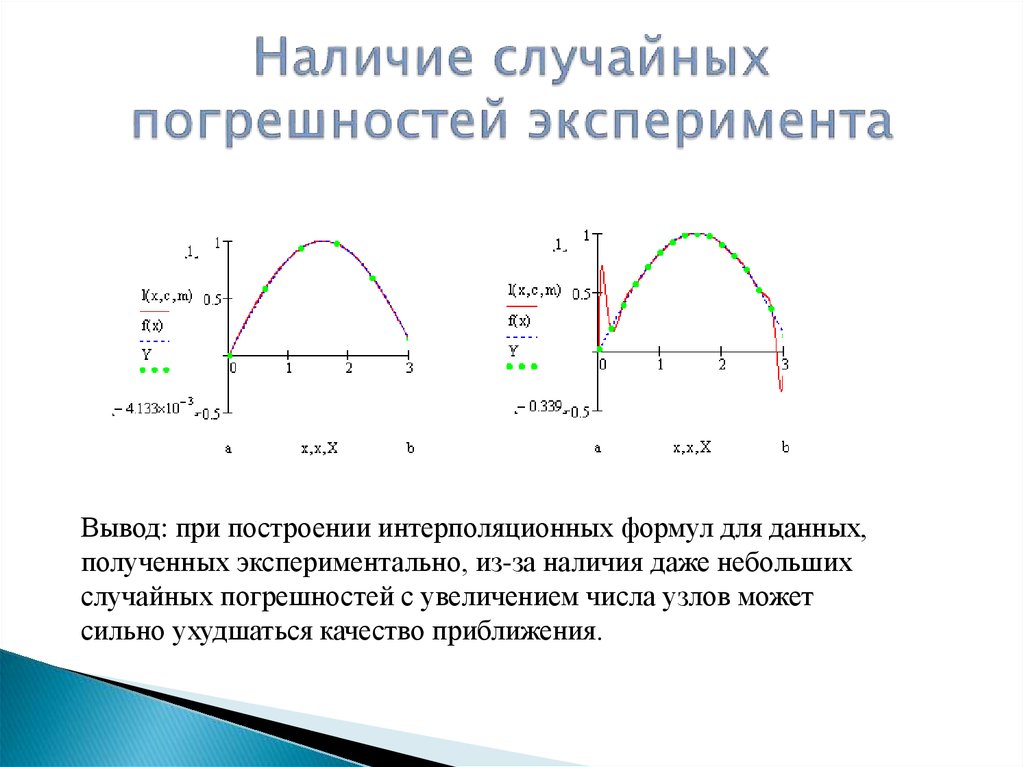
7. Наличие случайных погрешностей эксперимента
Вывод: при построении интерполяционных формул для данных,полученных экспериментально, из-за наличия даже небольших
случайных погрешностей с увеличением числа узлов может
сильно ухудшаться качество приближения.
8. Сплайн-интерполяция
На каждом промежутке xi 1 x xiстроится многочлен третьей степени
si x ai bi x xi
i 1,2,..., n
ci
x xi 2 d i x xi
2
6
коэффициенты которого находятся из условий
интерполяции и условий непрерывности первой и
второй производных. При этом получается система
линейных уравнений с трехдиагональной матрицей,
которая эффективно решается методом прогонки.
9.
Добавлены случайныеотклонения
Выводы: 1) качество приближения может ухудшаться
только в промежутках негладкости функции;
2) сплайн-интерполяция устойчива к случайным
погрешностям измерения.
10. Метод наименьших квадратов
Задача: требуется приблизить функцию y f (x) ,заданную таблицей своих значений в точках xi , i 1,2,..., n,
в некотором классе функций y F a0 , a1 ,..., am , x
Метод наименьших квадратов состоит в таком
подборе параметров a0 , a1 ,..., am , при котором сумма
квадратов отклонений значений функции F (a0 , a1 ,..., am , x)
от yi в точках xi минимальна.
В качестве функции F (a0 , a1 ,..., am , x) часто берут
многочлены, причем невысокой степени. Например
при m=2 МНК приводит к следующей системе
линейных уравнений:
11.
nn
n
2
xi a 2 xi y i
a 0 n a1
i 1
i 1
i 1
n
n
n
n
2
3
a 0 xi a1 xi a3 xi y i xi
i 1
i 1
i 1
i 1
n
n
n
n 2
3
4
2
a 0 xi a1 xi a3 xi y i xi
i 1
i 1
i 1
i 1
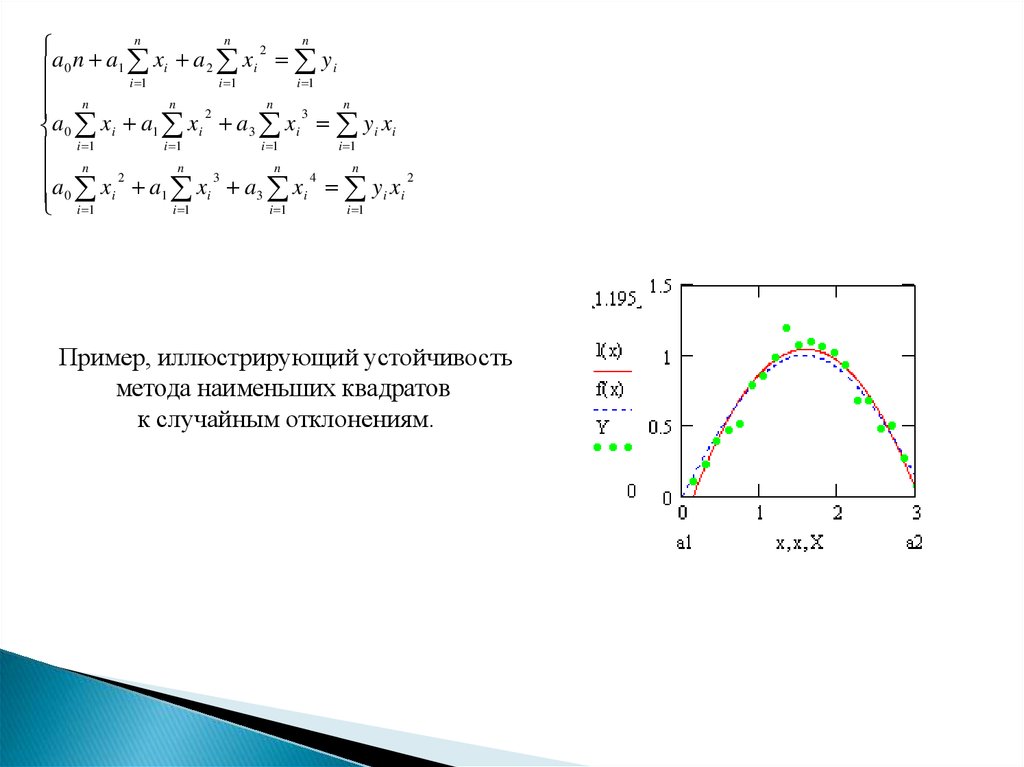
Пример, иллюстрирующий устойчивость
метода наименьших квадратов
к случайным отклонениям.
12. Выводы
1.2.
Не следует применять интерполяционные многочлены
Лагранжа и Ньютона высокой степени (с большим
количеством узлов) в случаях негладкой функции и при
наличии даже небольших случайных ошибок измерения.
Сплайн-интерполяцию и метод наименьших квадратов
можно использовать для большого количества узлов, в
том числе в случаях негладкой функции и при наличии
случайных ошибок измерения.









 mathematics
mathematics








