Формула Герона

1. Формула Герона

ФОРМУЛА
ГЕРОНА

2. Геро́н Александри́йский

ГЕРО́Н
АЛ Е К С А Н Д Р И́ ЙСКИЙ

3. ГЕРОН АЛЕКСАНДРИЙСКИЙ

Вероятно,
I – II вв н.э. древнегреческий
инженер, физик,
математик,
изобретатель

4.

Занимался геометрией,
механикой,
гидростатикой,
оптикой. Основные
произведения:
Метрика, Пневматика,
Автоматопоэтика,
Механика
(произведение
сохранилось целиком
в арабском переводе),
Катоптрика (наука о
зеркалах, отражениие
света); и др

5. ДИОПТРА – одно из изобретений Герона

ДИОПТРА – ОДНО ИЗ ИЗОБРЕТЕНИЙ ГЕРОНА
В 1814 году было найдено
сочинение Герона «О диоптре», в
котором изложены правила
земельной съёмки, фактически
основанные на использовании
прямоугольных координат.
Герон использовал достижения
своих предшественников:
Евклида, Архимеда. Многие из
его книг безвозвратно утеряны
(свитки содержались в
Александрийской библиотеке).
Одна из копий его книг,
сделанная в 16 веке, содержится
в Оксфордском Университете

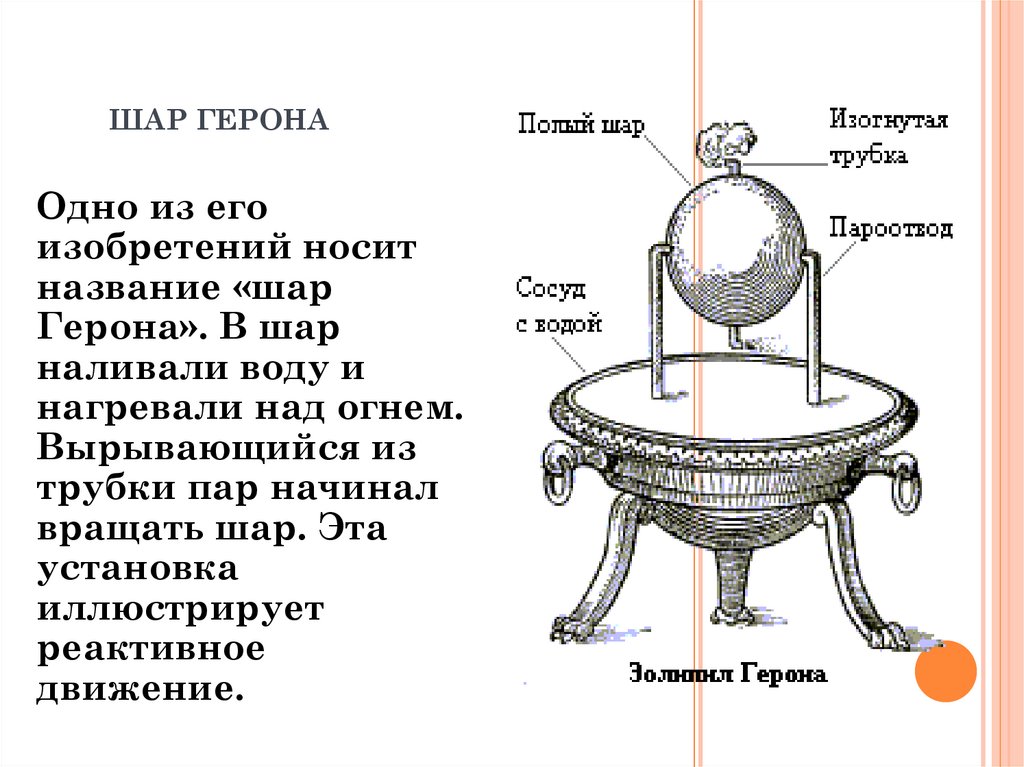
6. ШАР ГЕРОНА

Одно из его
изобретений носит
название «шар
Герона». В шар
наливали воду и
нагревали над огнем.
Вырывающийся из
трубки пар начинал
вращать шар. Эта
установка
иллюстрирует
реактивное
движение.

7. Задача Герона Александрийского

ЗАДАЧА ГЕРОНА АЛЕКСАНДРИЙСКОГО
Бассейн ёмкостью 12
кубических единиц
получает воду через
две трубы,из
которых одна дает в
каждый час
кубическую
единицу, а другая в
каждый час - четыре
кубические
единицы. В какое
время наполнится
бассейн при
совместном
действии обоих
труб?

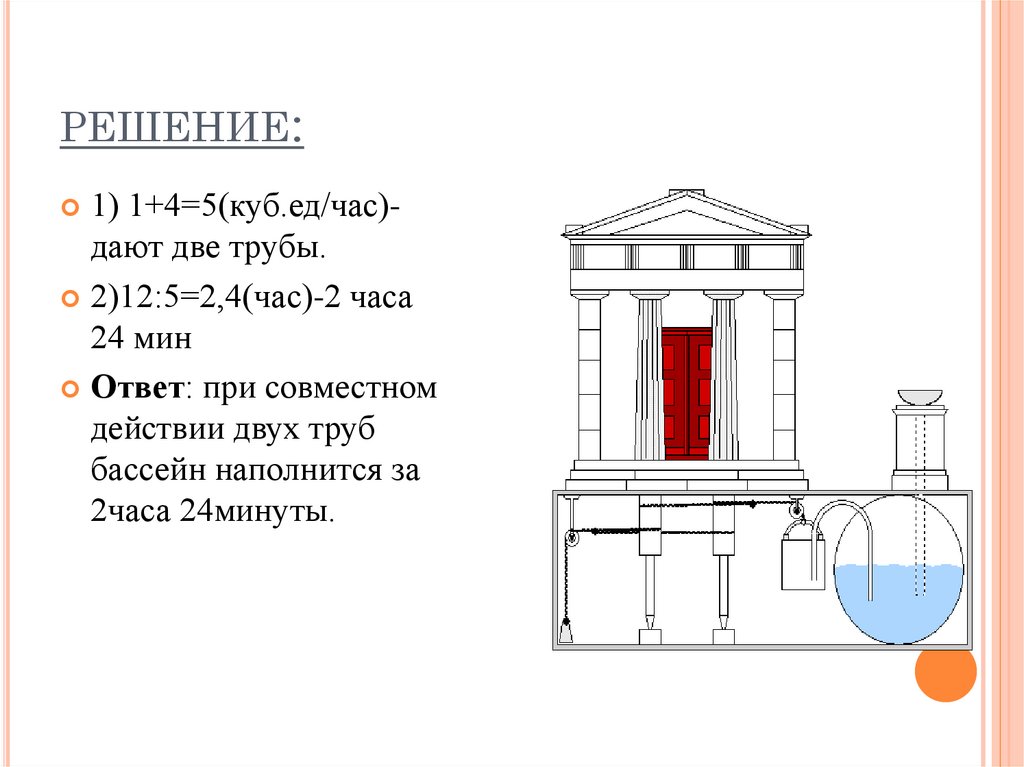
8. решение:

РЕШЕНИЕ:
1) 1+4=5(куб.ед/час)-
дают две трубы.
2)12:5=2,4(час)-2 часа
24 мин
Ответ: при совместном
действии двух труб
бассейн наполнится за
2часа 24минуты.

9. ТЕАТР ГЕРОНА

Этот театр (пинака) был очень
мал по своим размерам, его
легко переносили с места на
место, Он представлял собой
небольшую колонну, наверху
которой находился макет
театральной сцены, скрытой
за дверцами. Они открывались
и закрывались пять раз,
разделяя на акты драму о
печальном возвращении
победителей Трои. На
крошечной сцене с
исключительным мастерством
показывалось, как воины
сооружали и спускали на воду
парусные корабли, плыли на
них по бурному морю и
погибали в пучине под
сверкание молний и раскаты
грома. Для имитации грома
Герон создал специальное
устройство, в котором из
ящика высыпались шарики,

10. ФОРМУЛА ГЕРОНА

Формула очень важна с
практической точки
зрения - она позволяет
вычислять площадь
земельного участка по
длинам его сторон, очень
быстро.
Вспомним, в Древнем
Египте собирали урожай
два раза в год, а
восстанавливать границы
земельных участков
после разлива Нила в
жарком климате надо
было очень быстро, пока
земля не пересохла.

11.

Следствие.
Площадь равностороннего
треугольника со стороной а
выражается формулой
S
a
2
4
3

12. Решение задач на применение формулы Герона №1 (оформить решение)

РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ ФОРМУЛЫ ГЕРОНА
№1 (ОФОРМИТЬ РЕШЕНИЕ)
Дано: ABC треугольник,
AB=14см, BC=13см,
AC=15см.
Найти: SABC .

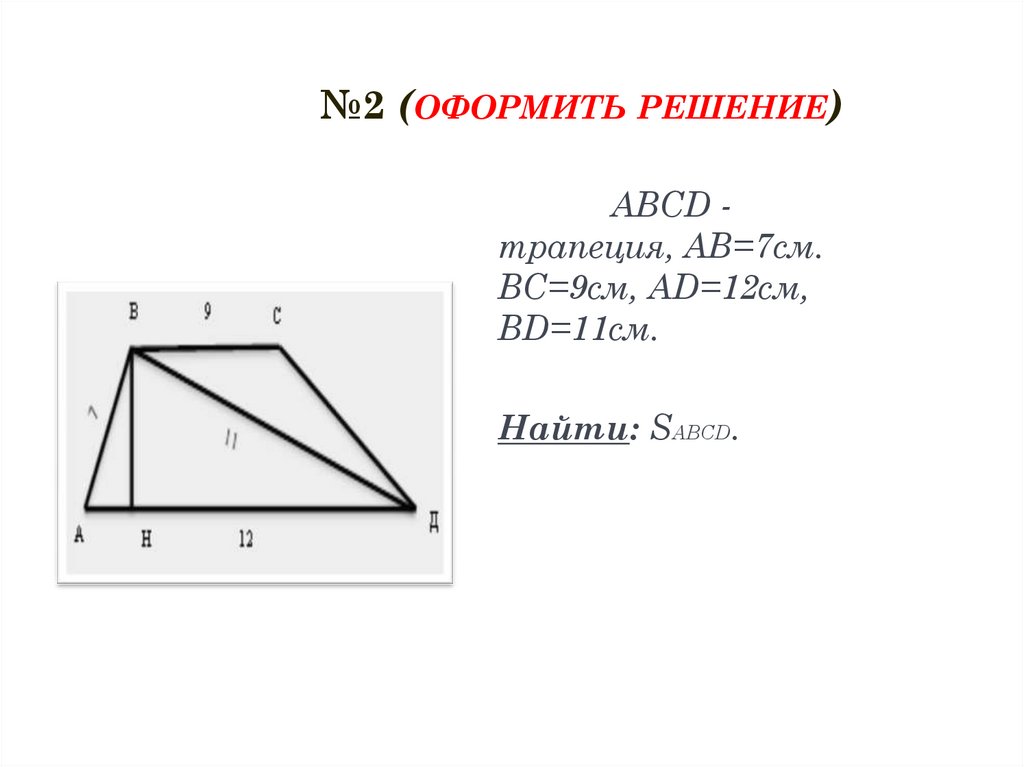
13. №2 (оформить решение)

№2 (ОФОРМИТЬ РЕШЕНИЕ)
Дано: ABCD трапеция, AB=7см.
BC=9см, AD=12см,
BD=11см.
Найти: SABCD.

14.

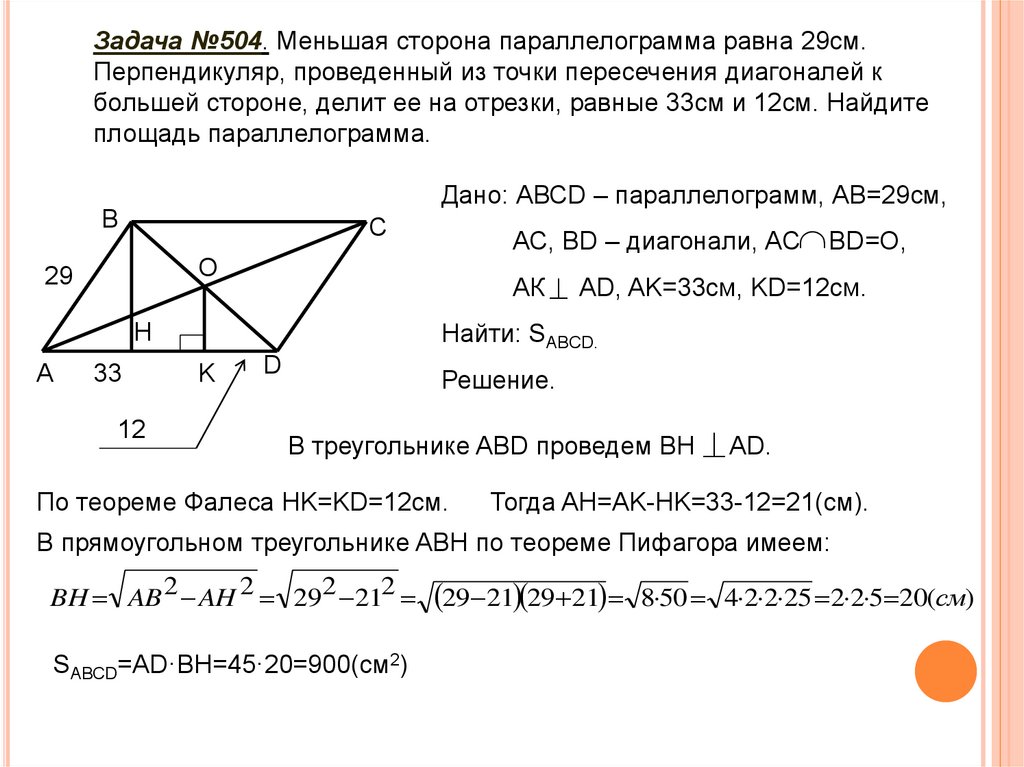
Задача №504. Меньшая сторона параллелограмма равна 29см.
Перпендикуляр, проведенный из точки пересечения диагоналей к
большей стороне, делит ее на отрезки, равные 33см и 12см. Найдите
площадь параллелограмма.
Дано: АВСD – параллелограмм, АВ=29см,
В
O
29
АК AD, AK=33см, KD=12см.
Найти: SABCD.
H
А
АС, ВD – диагонали, АС BD=O,
С
33
12
K
D
Решение.
В треугольнике ABD проведем BH AD.
По теореме Фалеса HK=KD=12cм.
Тогда AH=AK-HK=33-12=21(cм).
В прямоугольном треугольнике ABH по теореме Пифагора имеем:
BH AB 2 AH 2 292 212
SABCD=AD·BH=45·20=900(см2)
29 21 29 21 8 50 4 2 2 25 2 2 5 20(см)

15.

Задача №517. Найдите площадь четырехугольника ABCD, если AB=5см,
BC=13см, CD=9см, DA=15см, АС=12см.
1 способ
В
5
ABC
9
12
А
S
С
13
15
Применим к треугольникам ABC и ACD
формулу Герона.
p ABC
AB BC AC 5 13 12
15(см)
2
2
D
p p AB p BC p AC 15 15 5 15 13 15 12 15 10 2 3 5 3 5 2 2 3 5 3 2 30(см2 )
p ACD
AC CD AD 12 9 15
18(см)
2
2
S ACD 18 18 12 18 9 18 15 6 3 6 9 3 6 3 3 54(см2 )
SABCD=SABC+SACD=30+54=84(см2)

16.

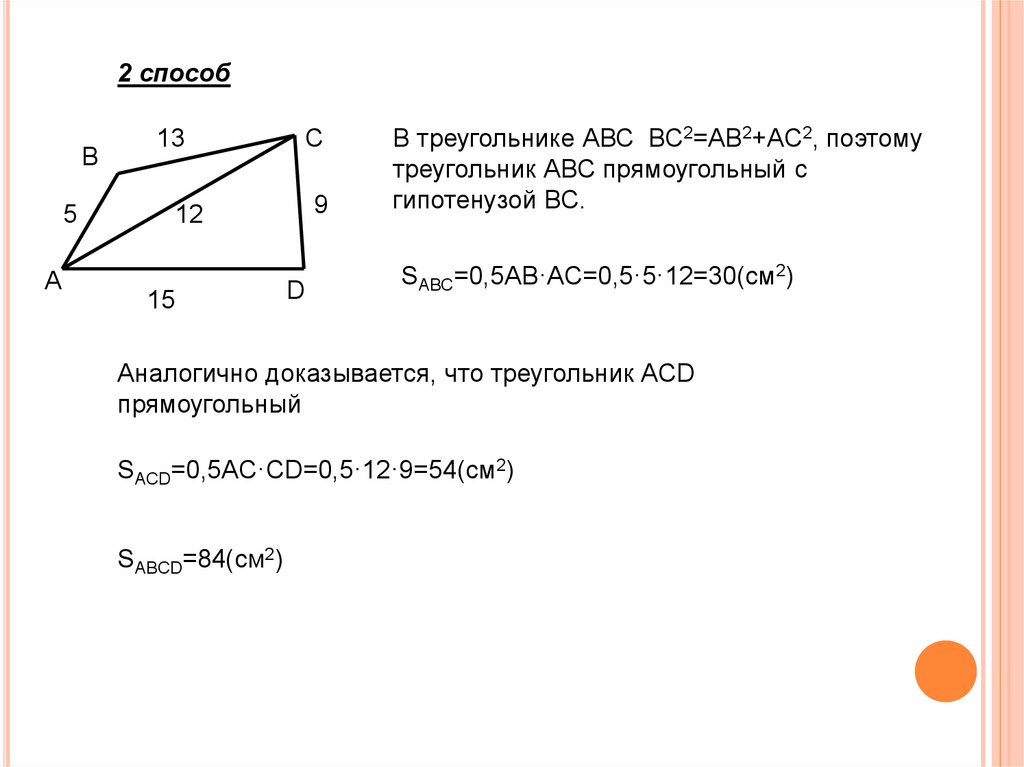
2 способ
В
5
А
С
13
9
12
15
D
В треугольнике АВС ВС2=АВ2+АС2, поэтому
треугольник АВС прямоугольный с
гипотенузой ВС.
SABC=0,5AB·AC=0,5·5·12=30(см2)
Аналогично доказывается, что треугольник ACD
прямоугольный
SACD=0,5AC·CD=0,5·12·9=54(см2)
SABCD=84(см2)