Площадь треугольника. Формула Герона

1. Площадь треугольника

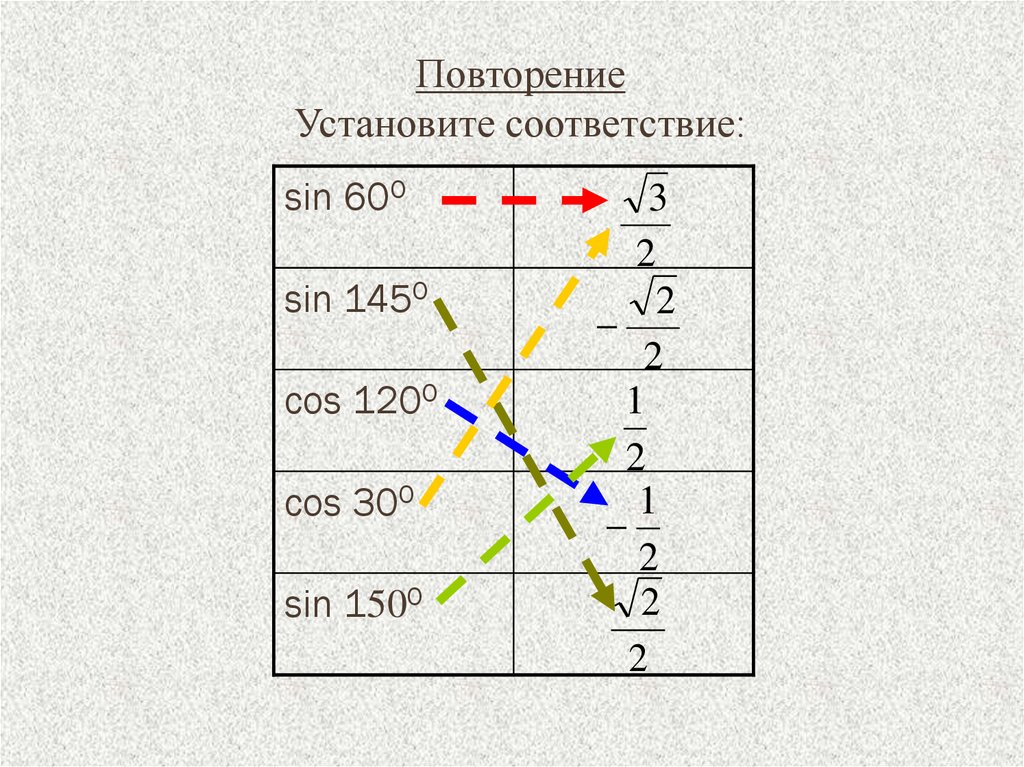
ПЛОЩАДЬ ТРЕУГОЛЬНИКА

2. Повторение Установите соответствие:

sin 600
sin 1450
cos 1200
cos 300
sin 1500
3
2
2
2
1
2
1
2
2
2

3.

1
1
1
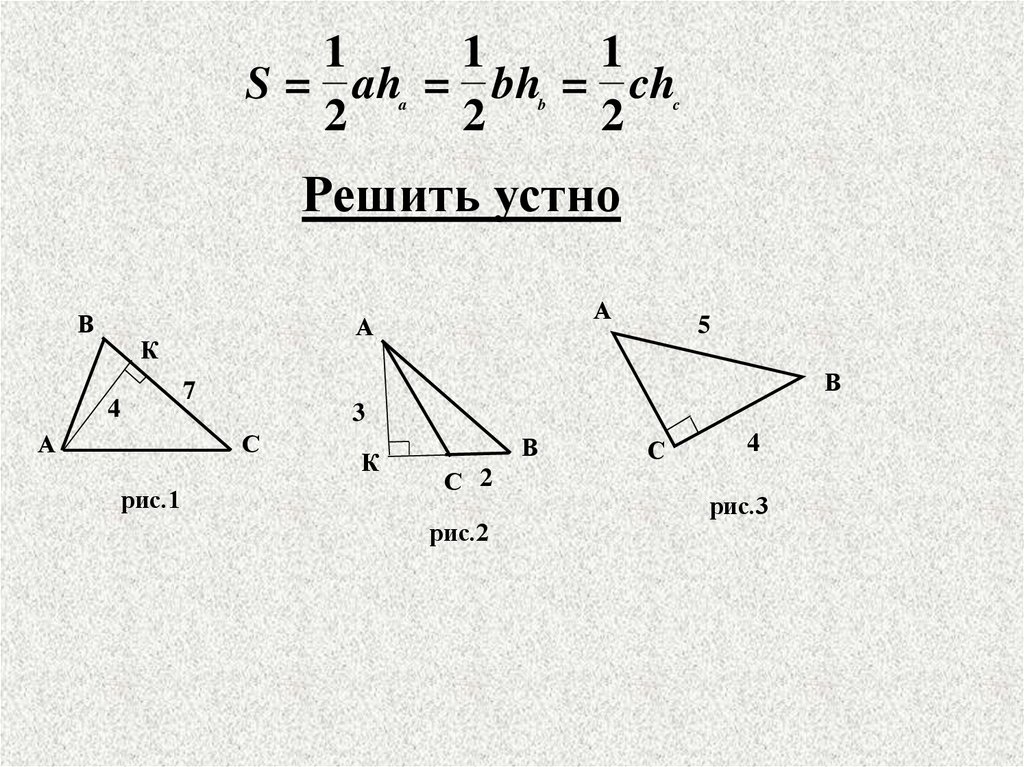
S = ah = bh = ch
2
2
2
a
b
c
Решить устно
В
К
А
3
С
рис.1
5
В
7
4
А
А
К
В
С 2
рис.2
С
4
рис.3

4.

1. Площадь прямоугольного треугольника
2. Площадь треугольника
3. Формула Герона
4. Площадь треугольника, вычисляемая с
помощью радиуса вписанной окружности
5. Площадь треугольника, вычисляемая с
помощью радиуса описанной
окружности

5.

1
S a b
2
А
b
В
С
a

6.

Решить устно
Найти площадь
треугольника, если:
с
b
1. а=8 см; b=3 см;
2. b=6 см; c=10 см.
a

7.

1
S ab sin
2
A
c
b
hа
С
ɣ
B
a
D
1
S ABC a ha , но из прямоугольного
2
треугольника ADC ha b sin , S ABC
1
ab sin
2

8.

Решить устно
а=12 см, b=9 см, ɣ=300.
Найти S.
№1
c
b
Ответ: S=27 см2.
ɣ
a
№2
α
b
α=800, ɣ=700, а=10 см,
с=8 см. Найти S.
c
ɣ
β
a
Ответ: S=20 см2.

9.

Угол при вершине равнобедренного треугольника равен
300, а его площадь – 150 см2. Найдите боковую сторону
треугольника.
Решение
В
А
Дан АВС ( АВ ВС ), В 30 , S ABC 150 см .
0
С
2
1
1
2
S ABC АВ ВС sin B AB sin B ;
2
2
2 S ABC
2 150
300
2
2
АВ
; АВ
300 2 600 ;
1
sin B
sin 30 0
2
АВ
600 10 6 ( см );
АВ ВС 10 6 ( см ).
Ответ : 10 6 см .

10.

Дан ΔАВС. Биссектриса угла В делит сторону АС на
отрезки 5 см и 6 см, начиная от вершины А. Сторона
АВ=15 см, угол С равен 300. Найти площадь и периметр
треугольника АВС.
·
Решение
Дан ΔАВС. АВ=15 см. Биссектриса ВК делит сторону
АС на отрезки: АК=5 см, КС=6 см.
Используя свойство биссектрисы угла, найдем ВС:
В
А
C
К
СВ АВ
СК ·AB
=
; СВ =
;
СК АК
АК
15·6
СВ =
= 18 см.
5
1
1
S = CВ·CА ·sin ∠ C, S = 18·11·sin30 =
2
2
99
=
= 49,5 ( см ).
2
P = AB + СВ + СА; P = 15 + 18 + 11 = 44 ( см ).
0
ΔABC
ΔABC
2
ΔABC
ΔABC
Ответ : 49,5 см ; 44 см.
2

11.

Формула Герона
с
a
b
a +b+c
S = p(p - a)(p - b)(p - c), p =
.
2

12.

Найдите площадь треугольника, стороны
которого равны 26 см, 28 см и 30 см. Найдите
высоту, проведенную к большей стороне.
Решение
Дан треугольник. а , b, c - его стороны.
а = 26 см, b = 28 см, с = 30 см.
a +b+c
S = p(p - a)(p - b)(p - c), p =
.
2
26 + 28 + 30
= 42( см ).
p=
2
S = 42(42 - 26)(42 - 28)(42 - 30) = 42·16·14·12 =
= 14·3·16·14·3·4 = 14·3·4·2 = 336 см .
2
1
2S
2·336
S = ch , h = . h =
= 22,4 см.
2
c
30
Ответ : 336 см ; 22,4 см.
c
c
c
2

13.

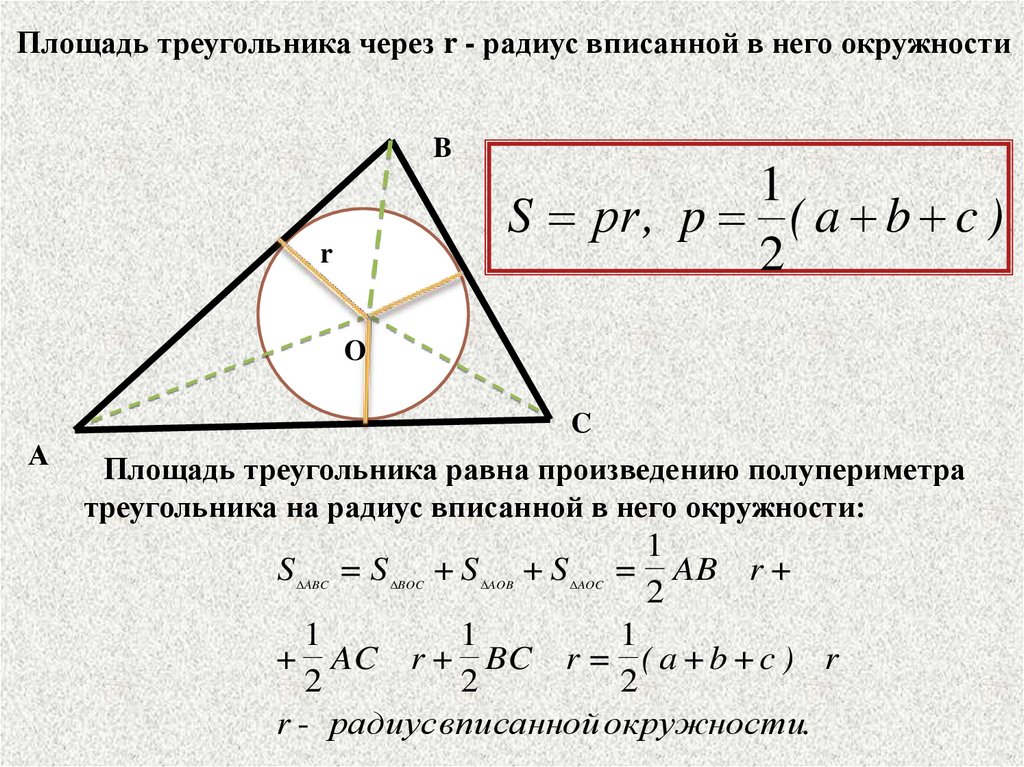
Площадь треугольника через r - радиус вписанной в него окружности
B
1
S рr , p ( a b c )
2
r
O
C
А
Площадь треугольника равна произведению полупериметра
треугольника на радиус вписанной в него окружности:
1
S = S + S + S = AB r +
2
1
1
1
+ AC r + BC r = ( a + b + c ) r
2
2
2
r - радиус вписанной окружности.
ΔABC
ΔBOC
ΔAOB
ΔAOC

14.

Решить самостоятельно:
1. Катеты прямоугольного треугольника 6 см, 8 см.
Найдите радиусы описанной и вписанной окружностей.
2. Стороны треугольника 4 см, 5 см и 7 см. Найти радиус
вписанной в треугольник окружности.
3. Стороны треугольника 5 см и 8 см, а угол между ними
600. Найти радиус окружности, вписанной в треугольник.

15.

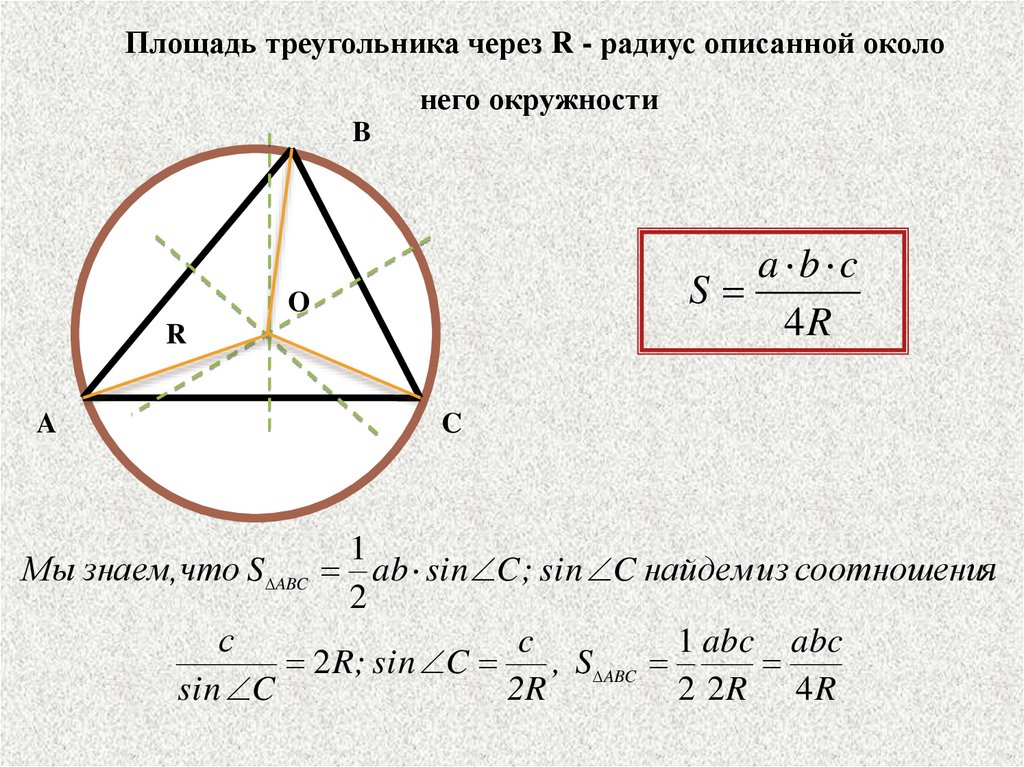
Площадь треугольника через R - радиус описанной около
него окружности
B
a b c
S
4R
O
R
A
C
1
Мы знаем, что S ABC ab sin C ; sin C найдем из соотношения
2
с
c
1 abc abc
2 R; sin C
, S ABC
sin C
2R
2 2R 4R

16.

B
c
A
a
b
C
a+ b+ c
p=
2
1
2
S
4ab (a b c )
4

17.

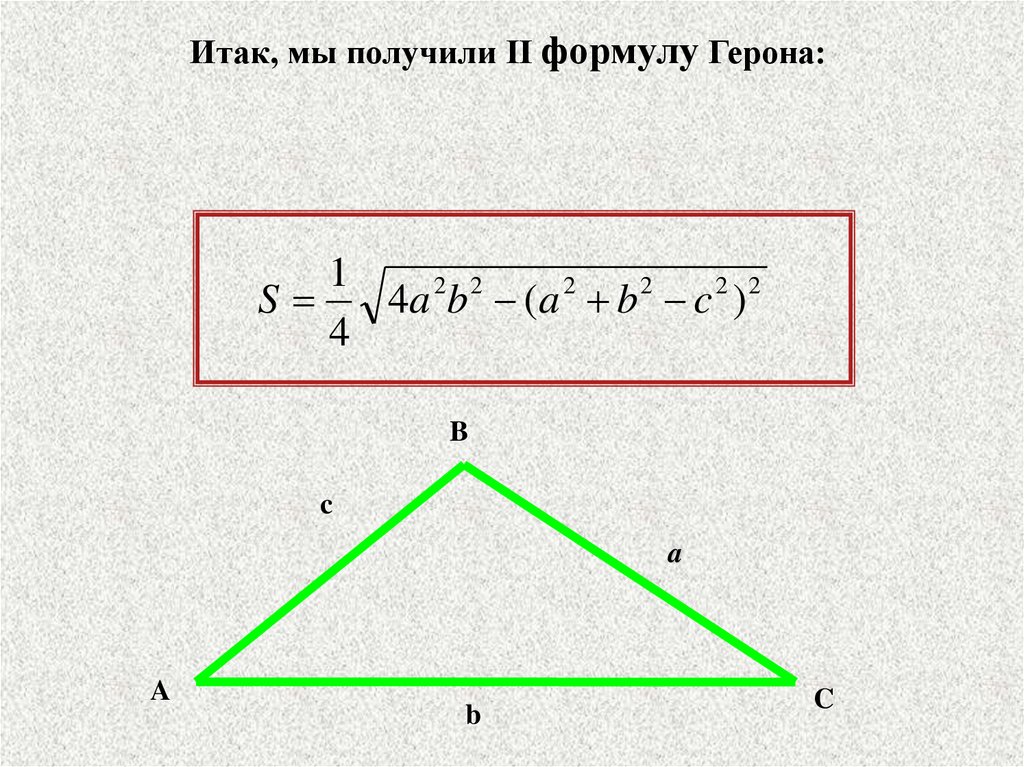
Итак, мы получили II формулу Герона:
1
2 2
2
2
2 2
S
4a b ( a b c )
4
B
c
a
A
b
C

18.

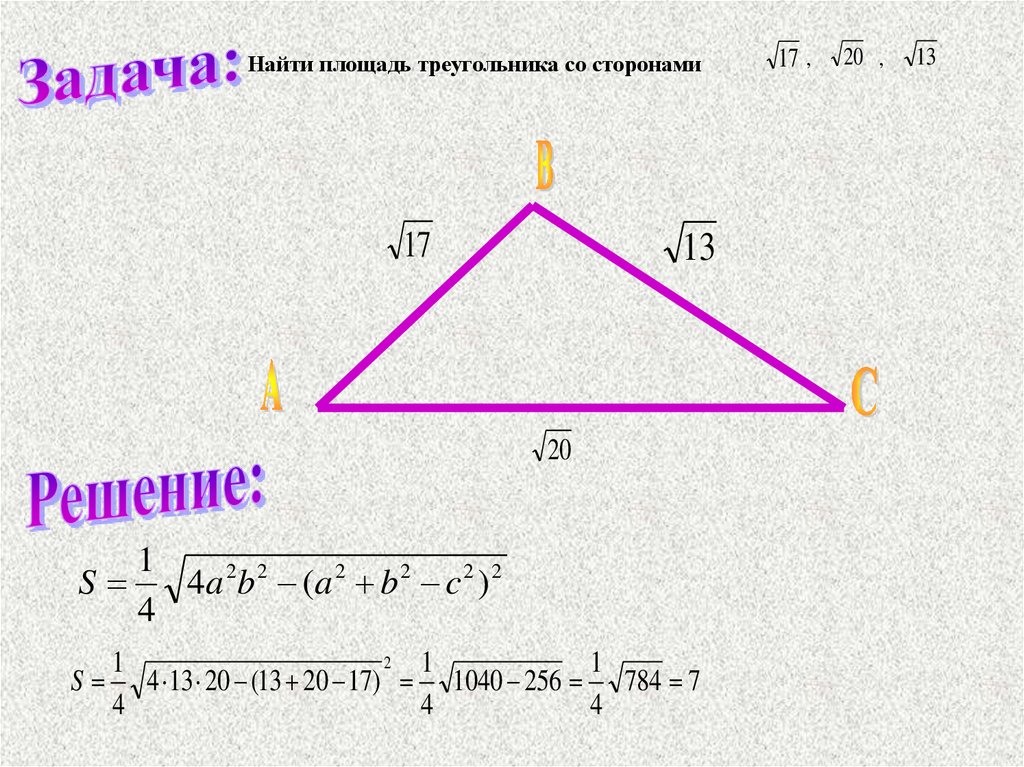
Найти площадь треугольника со сторонами
17
13
20
1
S
4a 2b 2 ( a 2 b 2 c 2 ) 2
4
2
1
1
1
S 4 13 20 (13 20 17) 1040 256 784 7
4
4
4
17 ,
20 ,
13

19. Теперь реши самые трудные задачи

ТЕПЕРЬ РЕШИ САМЫЕ ТРУДНЫЕ ЗАДАЧИ
1. Боковая сторона равнобедренного
треугольника равна a, а угол при
основании равен . Найдите площадь
треугольника.
2. Высота равностороннего треугольника
равна h. Вычислите его площадь.
3. В прямоугольном треугольнике гипотенуза
равна с, а один из острых углов равен .
Найдите площадь треугольника.
19