Формулы для вычисления площадей различных треугольников

1.

Формулы для вычисления площадей
различных треугольников

2.

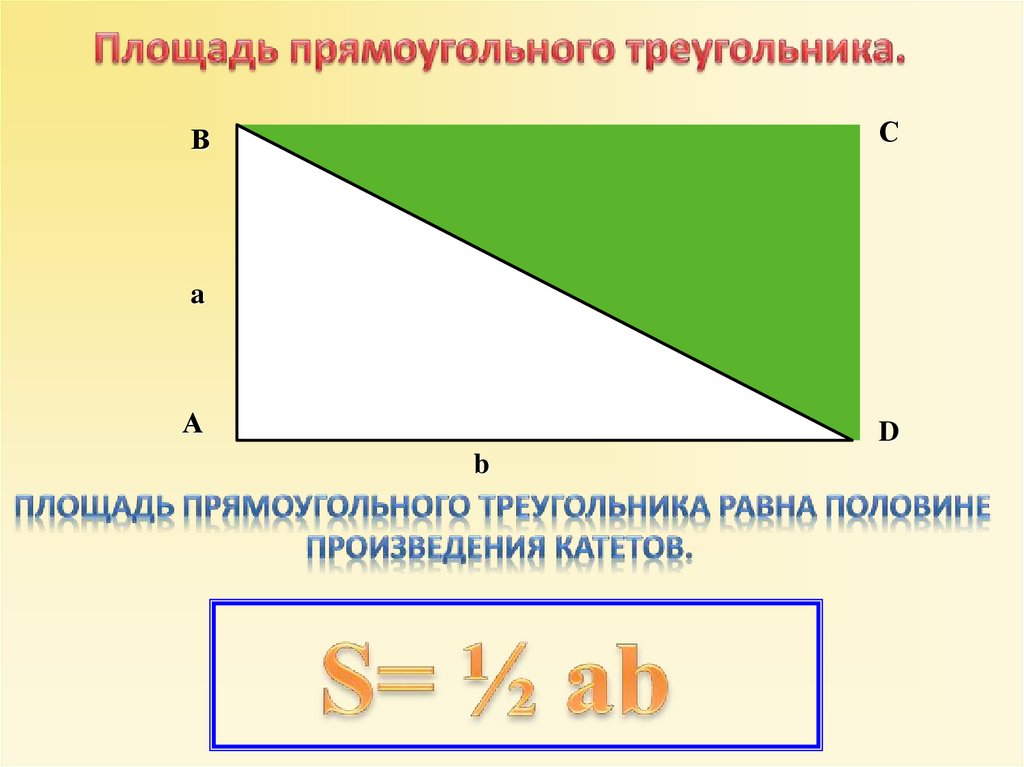
С
В
a
А
D
b

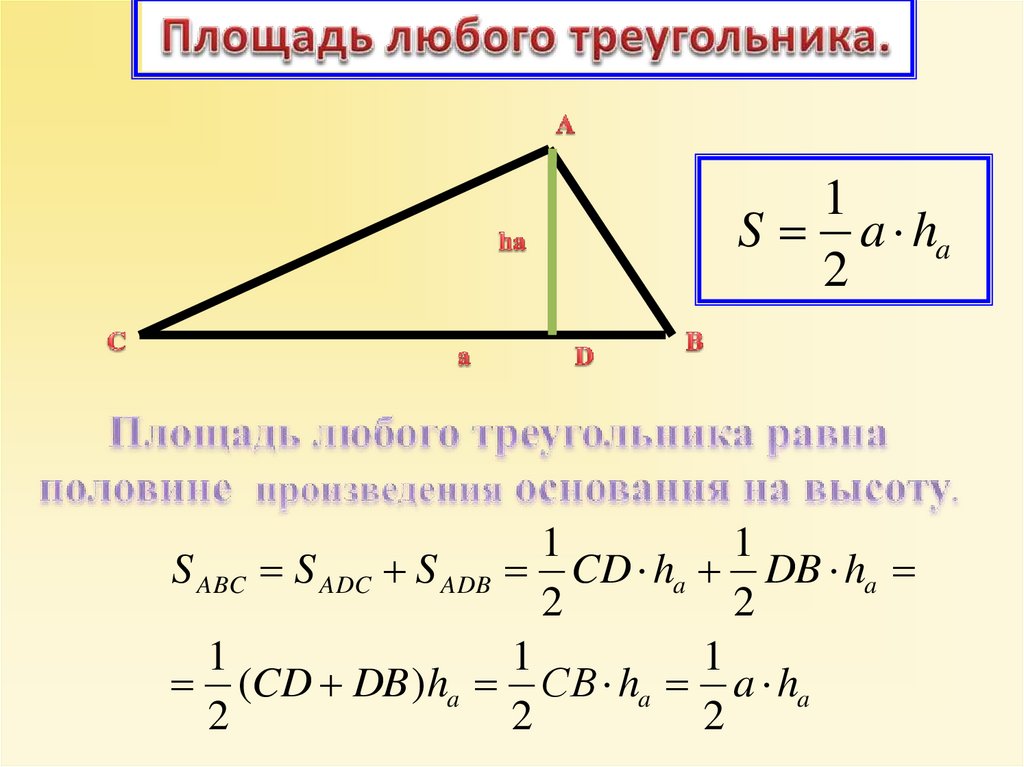
3.

1
S a ha
2
1
1
S ABC S ADC S ADB CD ha DB ha
2
2
1
1
1
(CD DB )ha СB ha a ha
2
2
2

4.

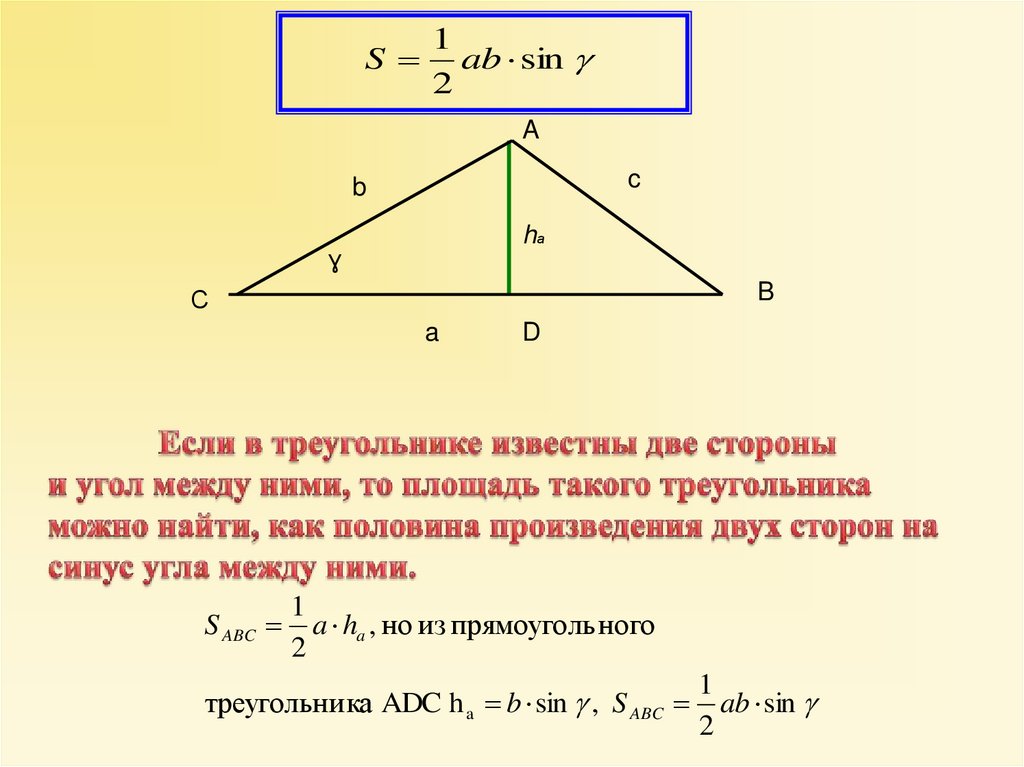
1
S ab sin
2
A
c
b
hа
ɣ
B
С
a
S ABC
D
1
a ha , но из прямоуголь ного
2
1
треугольни ка ADC h a b sin , S ABC ab sin
2

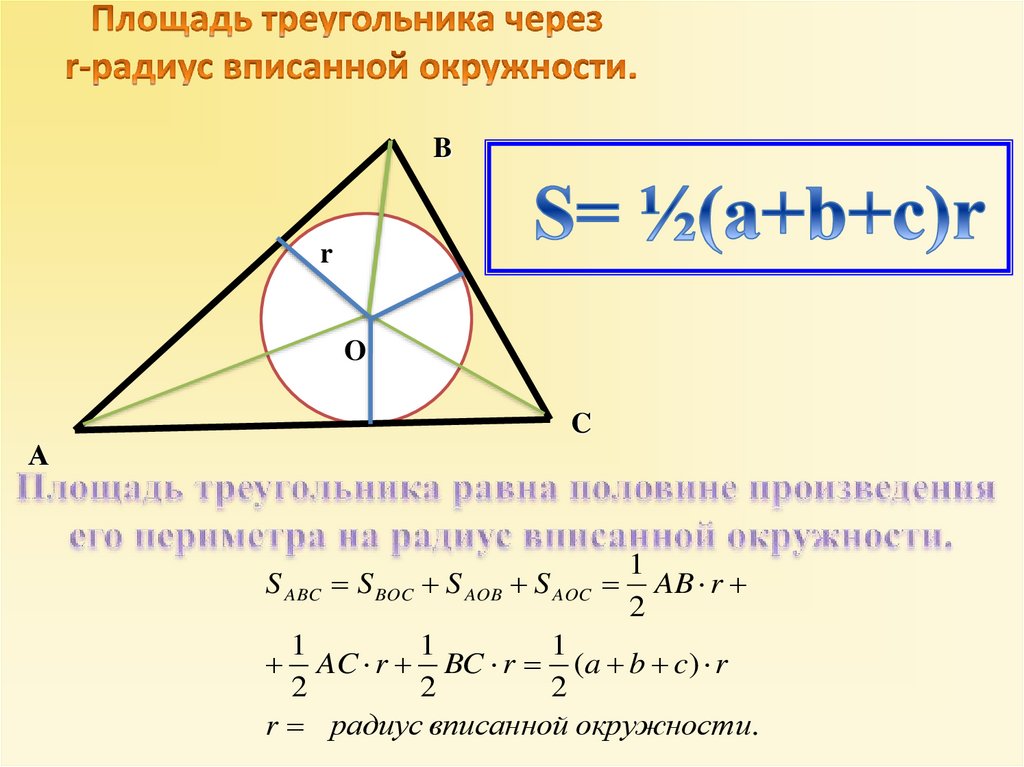
5.

B
r
O
C
А
1
S ABC S BOC S AOB S AOC AB r
2
1
1
1
AC r BC r (a b c) r
2
2
2
r радиус вписанной окружности.

6.

B
a b c
S
4R
O
R
A
C
1
ab sin C ; sin C найдем из соотношения
2
с
c
1 abc abc
2 R; sin C
, SABC
sin C
2R
2 2R 4R
Мы знаем, что SABC

7.

B
с
a
A
b
C
S p( p a)( p b)( p c)

8. ГЕРОН АЛЕКСАНДРИЙСКИЙ (Heronus Alexandrinus)

Герон Александрийский – греческий учёный,
работавший в Александрии,(даты рождения и смерти
неизвестны, вероятно, I – II вв. н. э. ).
Математические работы Герона являются
энциклопедией античной прикладной математики. В
"Метрике" даны правила и формулы для точного и
приближённого расчёта различных геометрических
фигур, например формула Герона для определения
площади треугольника по трём сторонам, правила
численного решения квадратных уравнений и
приближённого извлечения квадратных и кубических
корней. В основном изложение в математических
трудах Герона догматично – правила часто не
выводятся, а только выясняются на примерах.
Герон занимался геометрией, механикой,
гидростатикой, оптикой.

9.

B
c
A
a
C
b
1
S
4ab (a b c ) 2
4
p
a b c
2

10.

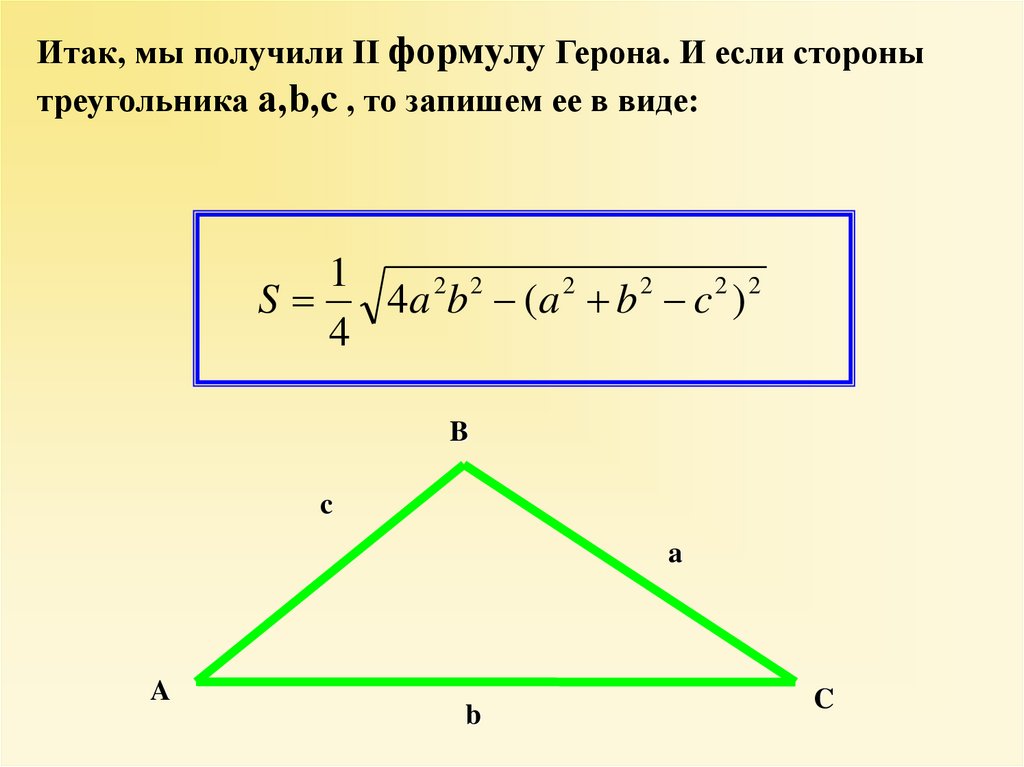
Итак, мы получили II формулу Герона. И если стороны
треугольника а,b,с , то запишем ее в виде:
1
2 2
2
2
2 2
S
4a b ( a b c )
4
B
c
a
A
b
C

11.

Найти площадь треугольника со сторонами
17
13
20
1
S
4a 2 b 2 ( a 2 b 2 c 2 ) 2
4
2
1
1
1
S 4 13 20 (13 20 17) 1040 256 784 7
4
4
4
17 ,
20 ,
13

12.

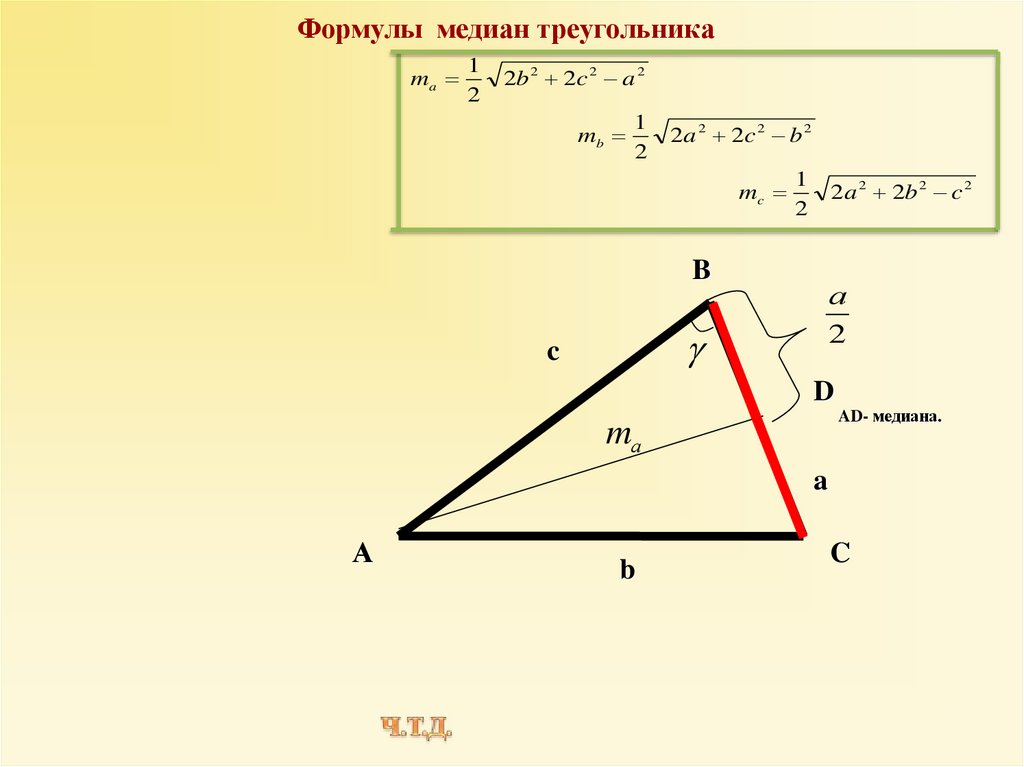
Формулы медиан треугольника
ma
1
2
2b 2 2c 2 a 2
mb
1
2
2 a 2 2c 2 b 2
mc
1
2
2a 2 2b 2 c 2
B
а
2
c
D
AD- медиана.
mа
a
А
b
C

13.

C
13
Дано : треугольник ABC
с 5
D
hc
а 10
10
в 13
Найти :
A
B
5
1) S ABC .
По второй формуле Ге рона:
2)hc .
1
4 ( 10 )2 ( 13 )2 (( 10 )2 ( 13 )2 ( 5 )2 )2
4
1
1
1
14 7
4 10 13 ( 10 13 5 )2
520 324
196
3,5
4
4
4
4 2
3) cos B.
1) S
4) R( радиус описанной окружности ).
5) Медиану AD
2) Проведем высоту СК hc ,
hc
2S
2 3,5
7
; hc
с
5
5
a2 c2 b2
,
2ac
( 10 )2 ( 5 )2 ( 13 )2 10 5 13
1
2
cos B
2 10 5
2 5 2
5 2 10
3 ) cos B
4) R
a b c
5 10 13 5 26
4S
4 3,5
14
5) Проведем медиану AD m a
ma
1
2b 2 2c 2 a 2 ,
2
ma
1
1
26
2 ( 13 ) 2 2 ( 5 ) 2 ( 10 ) 2
26 10 10
2
2
2

14.

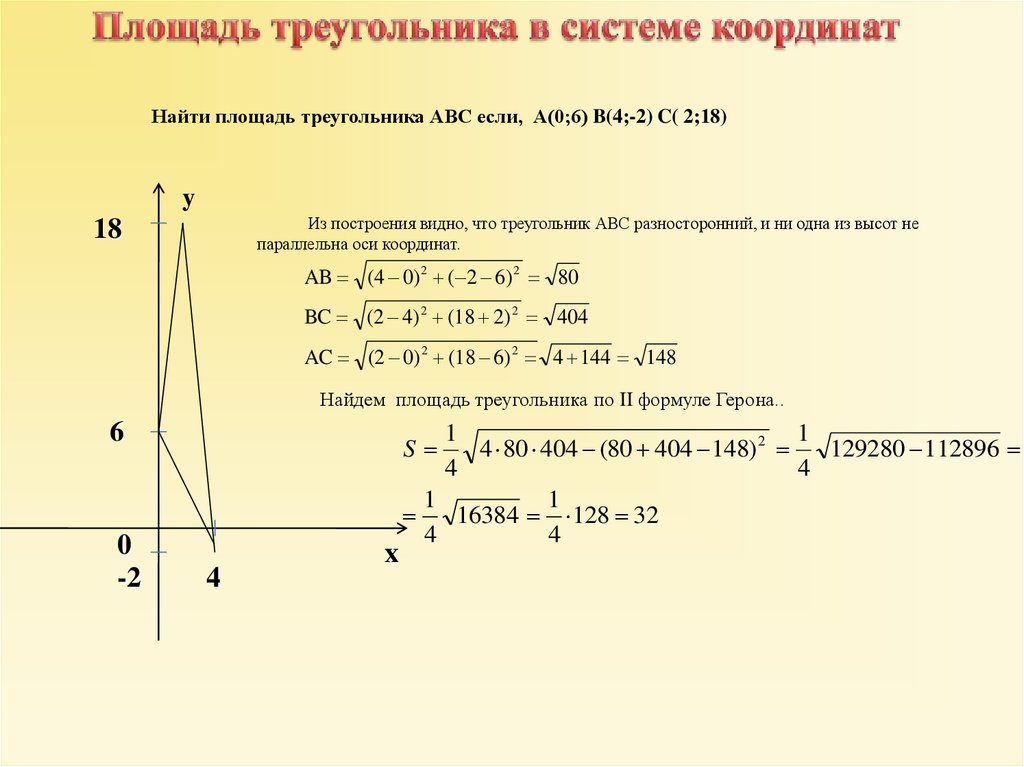
Найти площадь треугольника АВС если, А(0;6) B(4;-2) C( 2;18)
y
Из построения видно, что треугольник АВС разносторонний, и ни одна из высот не
параллельна оси координат.
18
AB (4 0) 2 ( 2 6) 2 80
BC (2 4) 2 (18 2) 2 404
AC (2 0) 2 (18 6) 2 4 144 148
Найдем площадь треугольника по II формуле Герона..
6
0
-2
1
1
4 80 404 (80 404 148) 2
129280 112896
4
4
1
1
16384 128 32
4
4
S
4
x

15.

Семь формул для нахождения
площадей различных треугольников.
1
S ab
2
1
S a ha
2
S p( p a)( p b)( p c)
1
2 2
2
2
2 2
S
4a b ( a b c )
4
1
1
S 2 ( a b c) r
S ab sin
2
a b c
S
4R

16.

С
Ɣ
в
а
А
α
β
с
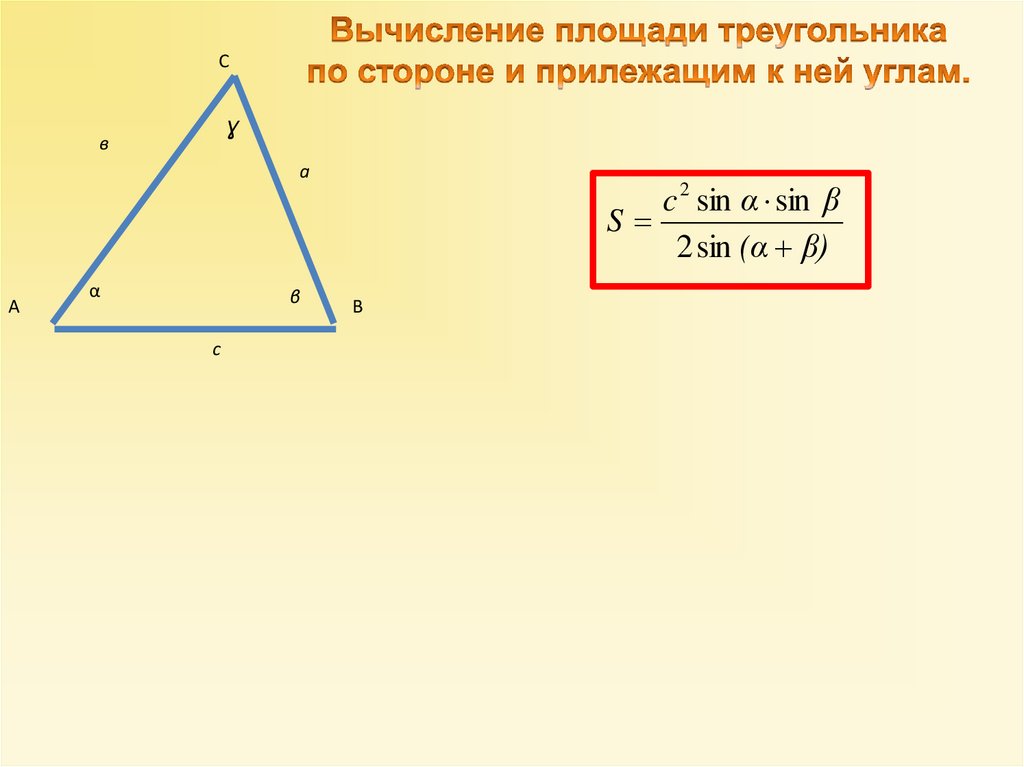
c 2 sin α sin β
S
2 sin (α β)
В

17.

С
Ɣ
в
S
а
А
α
β
с
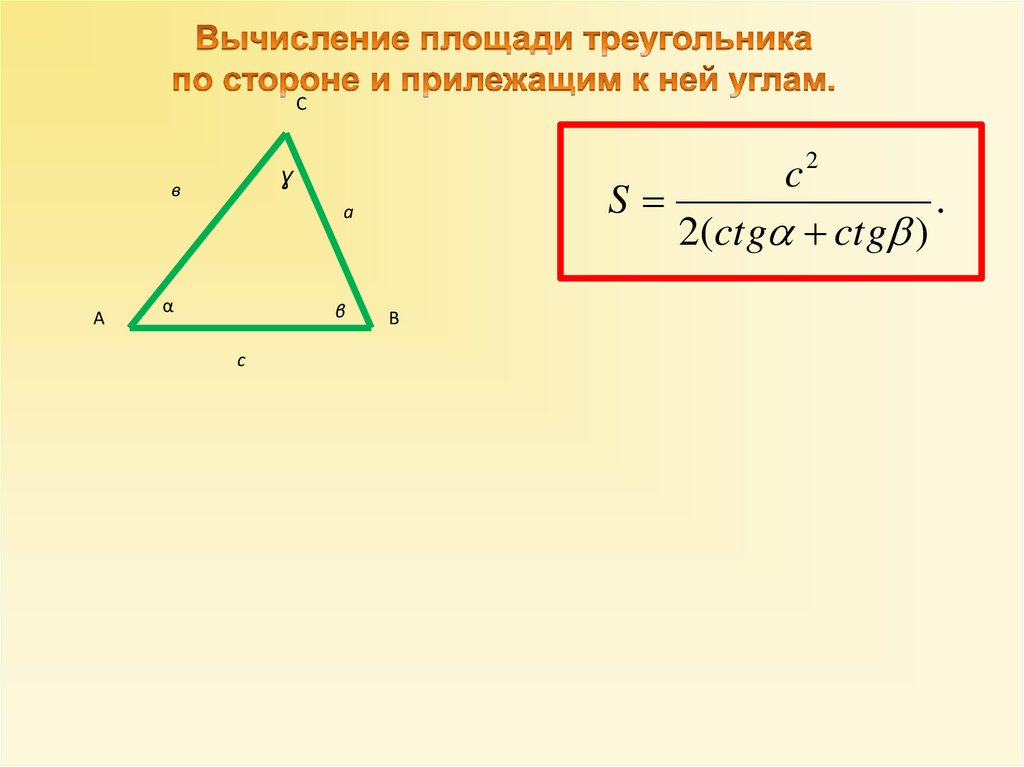
В
c
2
2(ctg ctg )
.

18.

B
S 2R sin sin sin .
O
A
2
C

19.

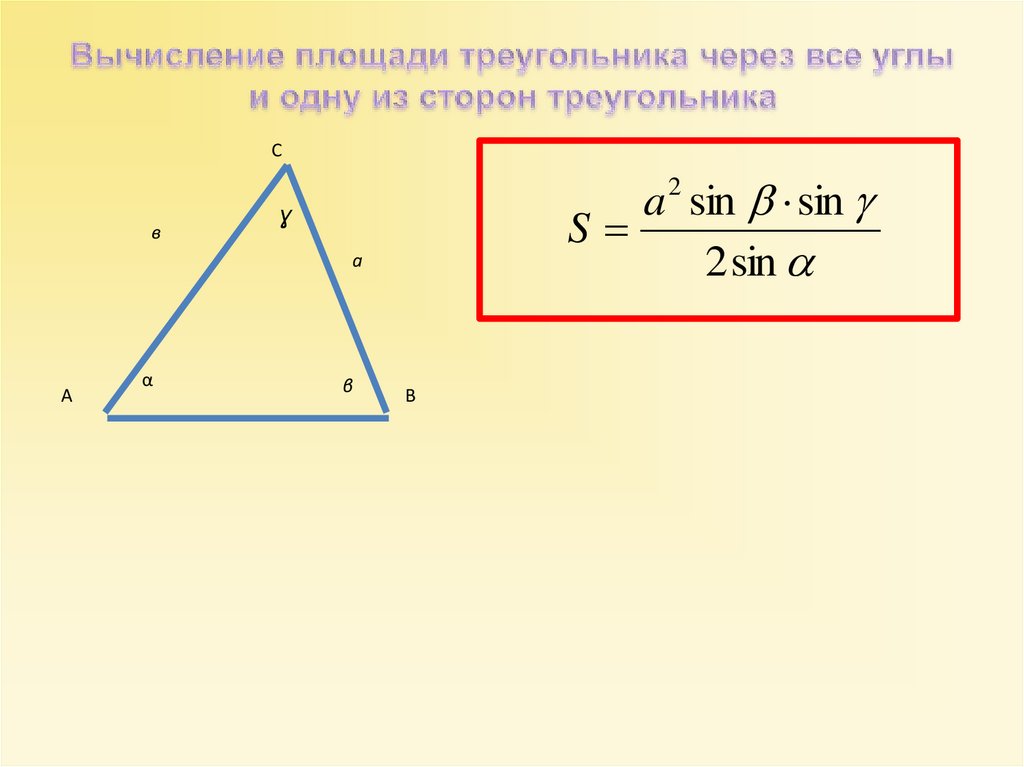
С
в
a 2 sin sin
S
2 sin
Ɣ
а
А
α
β
В

20.

Вычисление площади треугольника через радиусы
вневписанных окружностей.
Вневписанная окружность- это
окружность, касающаяся одной
стороны треугольника и продолжения
двух других сторон.
Oa
Oc
rа
S ra ( p a ) rb ( p b) rc ( p c)
rс
β
a
Ɣ
c
α
b
S ra rb rc r
ra , rb , rc радиусы вневписанных окружностей
rb
p полупериметр
Ob

21. Интернет-ресурсы

• Сайт http://www.webmath.ru
• Вычисление площади треугольника
• Формула площади треугольника, онлайн
сервис для расчета площади треугольника.
Нахождение площади треугольника 7-ю
методами, всего за несколько секунд Вы
найдете площадь треугольника.