Similar presentations:
Корень n-ой степени
1.
Корень n-ой степениn
а
2.
Понятие корня n-ой степениКорнем n-ой степени из неотрицательного
числа а (n = 2, 3, 4, 5, ...) называют такое
неотрицательное число, при возведении
которого в степень п получается число а.
n
a b , b n a , где a 0 , b 0 , n N , n 1
Число а называют подкоренным числом,
а число n – показателем корня
3.
Примеры1)
3
2)
4
3)
5
27 3;
33 27
256 4;
4 4 256
0,00243 0,3;
0,35 0,00243
100 3 1000000
4)
3
1000000 100 ;
5)
3
64000 40 ;
40 3 64000
1
1
;
64 2
6
6)
6
1
1
64
2
4.
Свойства корня n-ой степени(для n ∈ N, k ∈ N, n > 1, k > 1)
1
n
ab n a n b ,
где a 0, b 0
1)
4
16 625 4 16 4 625 2 5 10;
2)
3
4 3 16 3 4 16 3 64 4;
n
a
a
n
n ,
b
b
2
3)
4)
где a 0, b 0
5
19
243
243 3
5 7
5
5
1,5;
32
32
2
32
6
256 6 256 6
64 2;
6
4
4
5.
Свойства корня n-ой степени(для n ∈ N, k ∈ N, n > 1, k > 1)
a a , где a 0
3
k
n
k
n
4 4 16;
6)
81 3 3 ;
5)
2
3
5
5
4
3
n k
2
4
3
5
4
a nk a ,
где a 0
7)
3
729 6 729 3;
8)
3 5
а15 15 а15 а;
6.
Свойства корня n-ой степени(для n ∈ N, k ∈ N, n > 1, k > 1)
5
9)
np
12
a kp n a k ,
где a 0
a9 4 a3 ;
с 3 с 6 с3 6 с2 6 с3 с2 6 с5 ;
10)
6
n
11)
8
12)
11
a , n четно
a
a , n нечетно
n
( 3,25)8 3,25 3,25;
т11 т;
7.
ny
x
Функции вида
Свойства функции y n x , n – чётное число
1. D(у) = [0; + ).
2. E(у) = [0; + ).
3. Функция ни чётная, ни нечётная.
4. а) Нули функции: (0; 0).
б) Точка пересечения с Оу: (0; 0).
5. [0; + ) – промежуток возрастания функции;
6. Ограничена снизу, не ограничена сверху.
7. а) унаим. = 0;
б) унаиб. – не существует.
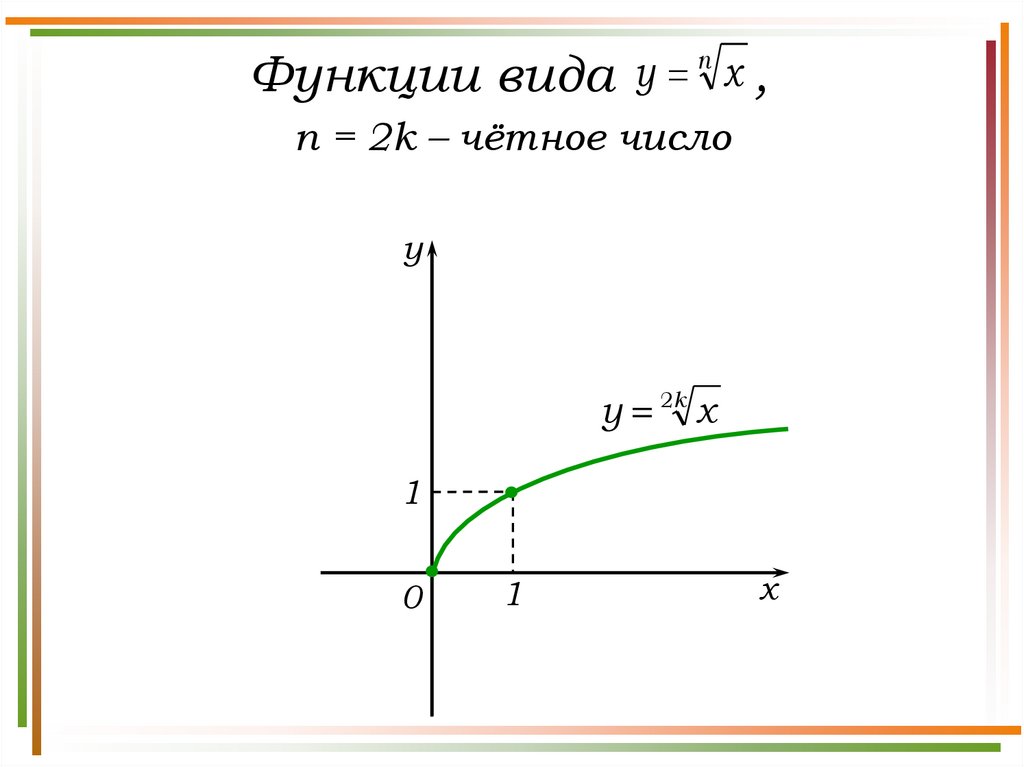
8.
ny
x,
Функции вида
n = 2k – чётное число
y
y 2k x
1
0
1
x
9.
ny
x
Функции вида
Свойства функции y n x , n – нечётное число
1. D(у) = (- ; + ).
2. E(у) = (- ; + ).
3. Функция нечётная.
4. а) Нули функции: (0; 0).
б) Точка пересечения с Оу: (0; 0).
5. (- ; + ) – промежуток возрастания функции;
6. Не ограничена снизу, не ограничена сверху.
7. а) унаим. – не существует;
б) унаиб. – не существует.
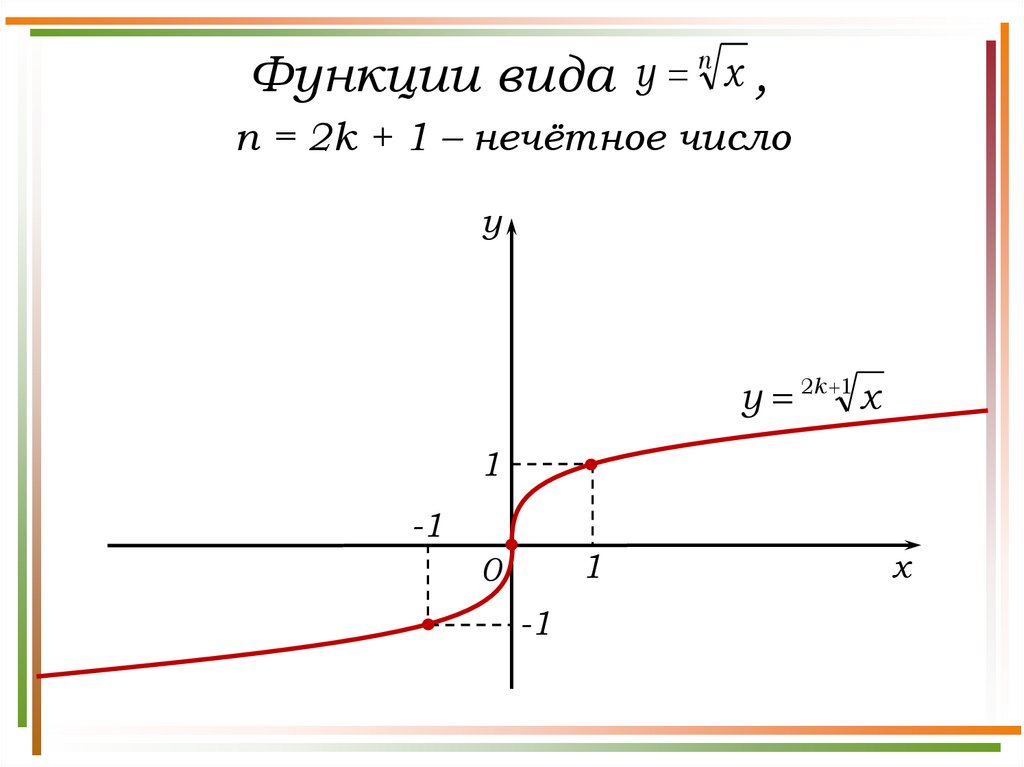
10.
ny
x,
Функции вида
n = 2k + 1 – нечётное число
y
y 2k 1 x
1
-1
1
0
-1
x
11.
Задания открытого банка задач1. Найдите значение выражения
652 562.
Решение.
652 562 (65 56)(65 56) 9 121 3 11 33.
2 7 .
2
2. Найдите значение выражения
Решение.
14
2 7 4 7 28 2.
2
14
14
14
3. Найдите значение выражения 13 7 13 7 .
Решение.
13 7 13 7 13 7 13 7 6.
2
2
12.
Задания открытого банка задач4. Найдите значение выражения
Решение.
6
5
3
3 1 :
.
7
7
28
27
27
6
5
3
12
3
12 28
3 1 :
:
7
7 28 7
7 28 7
7
3
27 28
12 28
27 28
12 28
9 4 4 4 6 4 2.
7
3
7
3
7 3
7 3
5. Найдите значение выражения
Решение.
9
9
7 18 7
.
6
7
7 18 7 18 72 18 7 18 72 7 18 73 18
1 1.
3
3
6
18 3
7
7
7
7
13.
Задания открытого банка задач6. Найдите значение выражения
Решение.
5
5
10 5 16
.
5
5
10 5 16 5 10 16 5
32 2.
5
5
5
7. Найдите значение выражения
Решение.
2 2
12
2
1
3
1
4
2
2 2
1
212
1
3
1
4
2
13 14
2 2
12 .
2
2
1 1 1 2
4 3 1 2
1 2
3 4 12
12
2
2 2.
2
2











 mathematics
mathematics








