Корень n-ой степени

1.

Корень n-ой степени
n
а

2.

Понятие корня n-ой степени
Корнем n-ой степени из неотрицательного
числа а (n = 2, 3, 4, 5, ...) называют такое
неотрицательное число, при возведении
которого в степень п получается число а.
n
a b , b n a , где a 0 , b 0 , n N , n 1
Число а называют подкоренным числом,
а число n – показателем корня

3.

Примеры
1)
3
2)
4
3)
5
27 3;
33 27
256 4;
44 256
0,00243 0,3;
0,35 0,00243
100 3 1000000
4)
3
1000000 100 ;
5)
3
64000 40 ;
6)
6
1
1
;
64 2
40 3 64000
6
1
1
64
2

4.

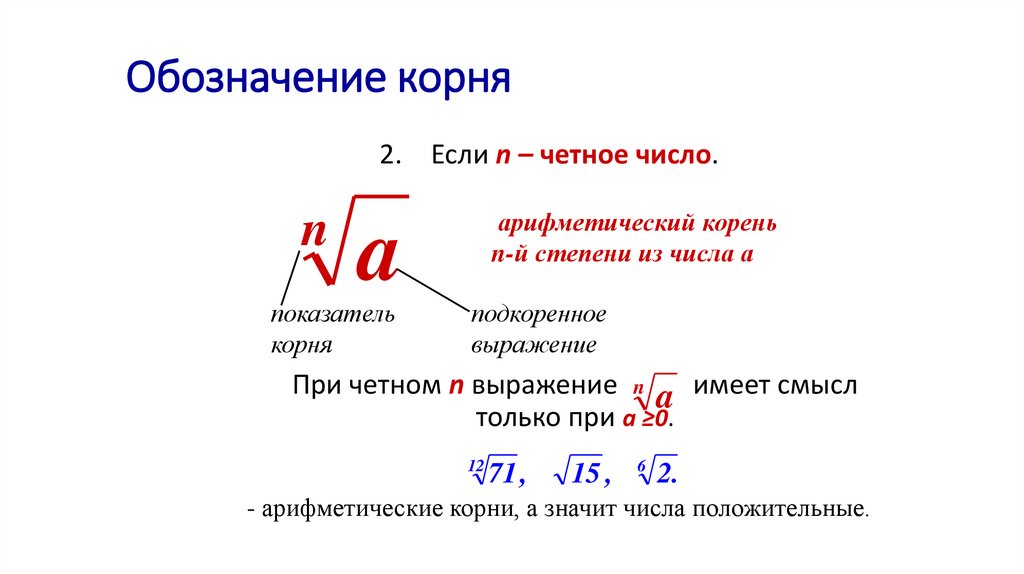
Обозначение корня
2. Если n – четное число.
n
арифметический корень
n-й степени из числа а
a
показатель
корня
подкоренное
выражение
При четном n выражение n a имеет смысл
только при а ≥0.
12
71 ,
15 ,
6
2.
- арифметические корни, а значит числа положительные.

5.

Свойства корней n-й степени
Теорема.
Пусть n
- нечетное число.
Пусть n
- четное число.
Тогда при любом значении а верны равенства:
a n a,
n
-a a
n
n
b 15 b 5
125 3 5 3 5
3
3
a | a |,
n
n
b 12 | b 3 |
16 4 2 4 | 2 | 2
4
4

6.

Свойства корня n-ой степени
(для n ∈ N, k ∈ N, n > 1, k > 1)
1
n
1)
4
2)
3
4)
n
где a 0, b 0
b,
16 625 4 16 4 625 2 5 10;
2
3)
ab n a
4 3 16 3 4 16 3 64 4;
n
a na
n ,
b
b
где a 0, b 0
19 5 243
5 7
32
32
6
243 3
1,5;
5
2
32
5
256 6 256 6
64 2;
6
4
4

7.

Свойства корня n-ой степени
(для n ∈ N, k ∈ N, n > 1, k > 1)
a
3
5)
6)
n
4
2
3
5
4
k
n ak ,
3 42 3 16;
81 3
5
n k
где a 0
4
3 ;
5
4
a nk a ,
где a 0
7)
3
729 6 729 3;
8)
3 5
а15 15 а15 а;

8.

Свойства корня n-ой степени
(для n ∈ N, k ∈ N, n > 1, k > 1)
5
9)
np
12
где a 0
a9 4 a3 ;
с 3 с 6 с3 6 с2 6 с3 с2 6 с5 ;
10)
6
a kp n a k ,
n
a , n четно
a
a , n нечетно
n
( 3,25)8 3,25 3,25;
11)
8
12)
11
т11 т;

9.

Свойства корня n-ой степени
(для n ∈ N, k ∈ N, n > 1, k > 1)
7
n
a n a , n нечетно
13)
7
128 7 128 2;
14)
8
3
0,000125 3 0,000125 0,05;
k
n
a n ak ,
см. далее
где a 0