Similar presentations:
Корень n-ой степени. Свойства корня
1.
МатематикаТема «Корень n-ой
степени.Свойства корня
Автор презентации: Дегтярева МВ
Дата создания презентации: 2.10.2018
2.
Вопросы:Квадратный корень
(определение,
примеры)
Корень n-ой степени
(определение,
примеры)
Свойства корня n-ой
степени
3.
I.Квадратный корень
(определение, примеры)
Квадратный корень из числа
2
36 6
49 7
4 2
а— это такое число, квадрат которого равен а
22 4 2
- показатель корня
2 25 2 5 10
21 5 16 4
4.
Корень n й степениЛюбое решение уравнения
x b, n 2,3,...
n
называется корнем n – й степени из
числа b.
5.
Обозначение арифметического корняПри n = 2 корень из
числа b обозначается
b
При n = 3, 4, …
корень из числа b обозначается
n
b
6.
Понятие корня n-ой степениКорнем n-ой степени из неотрицательного
числа а (n = 2, 3, 4, 5, ...) называют такое
неотрицательное число, при возведении
которого в степень п получается число а.
n
a b , b n a , где a 0 , b 0 , n N , n 1
Число а называют подкоренным числом,
а число n – показателем корня
7.
a b, b a, a 0, b 02
n
1.
n четное
a 0, b 0
2.
a b, b n a
n нечетное
a, b любые
a
a
n
2
a, a 0
n
a
8.
Корень n-ой степени(определение, примеры)
n –ой степени из числа «а» называется такое
число, n –ая степень которого равна «а».
Корнем
3
27 3 так
как 3 3 3 3 27
3
Найти значение числового выражения
3
4
27 3
81 3
16 2
4
6
625
1
1
64 2
5
7
128 2
5
1
1
2
32
9.
Примеры1)
3
27 3 ;
3 3 27
2)
4
256 4 ;
3)
5
0,00243 0,3;
4)
3
1000000 100 ;
5)
3
64000 40 ;
6)
6
1
1
;
64 2
4 4 256
0,35 0,00243
100 3 1000000
40 64000
3
6
1
1
64
2
10.
Способы извлечения квадратныхкорней:
1. По таблице;
2. Алгебраический;
3. Древневавилонский: c
Пример:
1700
b
a b a
2a
2
100
1600 100 40
41,25
80
Выполни по
3821 образцу:
11.
Операция извлечение корня является обратнойпо отношению к возведению в соответствующую
степень.
Возведение в степень
5² = 25
10³ = 1000
0,3⁴ = 0,0081
n
Извлечение корня
25
=
5
3
1000
=
10
4
0,0081 = 0,3
Иногда выражение a называют радикалом от
латинского слова radix – «корень».
Символ - это стилизованная буква r.
12.
Извлечение корней третьей степени.Подсказка.
13 1;
4 3 64;
7 3 343;
2 3 8;
5 3 125;
8 3 512;
33 27;
6 3 216;
9 3 729.
Образец.
3
3
274625 ;
571787 83
Реши сам:
3
6859 .
13.
Свойства корня n-ой степени(для n ∈ N, k ∈ N, n > 1, k > 1)
1
n
ab n a
2
n
a na
n ,
b
b
3
a
k
n
4
n k
5
np
6
n
7
n
8
n
n
b,
где a 0 , b 0
где a 0 , b 0
ak ,
a nk a ,
где a 0
где a 0
a kp n a k ,
где a 0
a , n четно
a
a , n нечетно
n
a n a , n нечетно
k
n
a n ak ,
где a 0
14.
Упростите выражения:5
8 4
5
4
1
5
16
3 5
21
7
128
8 4
5
5
32
4
4
81
81
4
16
16
15
7
21
2
7
3
2
5
2
5
3
1,5
2
2
15.
a2
a
a, если a < 0
a, еслиa 0
a b
2
a b
a b, если a b b a, если a b
16.
Работаем устно:1. Какие выражения имеют смысл:
1;
4
4 ; 3 8 ; 3 27 ; 3 1; 4 5 ;
16 ; 3 1; 3 27 ;
8;
9 ; 4 16 ; 8 1;
4 ; 3 9 ; 5 32 ?
2. При каких значениях a имеет смысл
выражение:
2
3
2
a, a , a, a , a , a5 ;
3
3. Вычислить:
a; 4 a;5 a2 ; 6 a3 ?
100 ; 5 100000 ;
3
0,001;
3
125
;
27
6,25 ; 4 81;
0,16 ;
4
81
.
16
17.
Вычислить18.
Вычислить19.
Понятие степени с рациональнымпоказателем
p
q
q
a a , где a 0 , q N , p Z
p
Примеры
1)
2)
3)
2
3
5 3 5 2 3 25
7
5
121,4 12 5 127
4
9
2
2
5
4
9
12
5
4
9
5
12
12
9
4
5














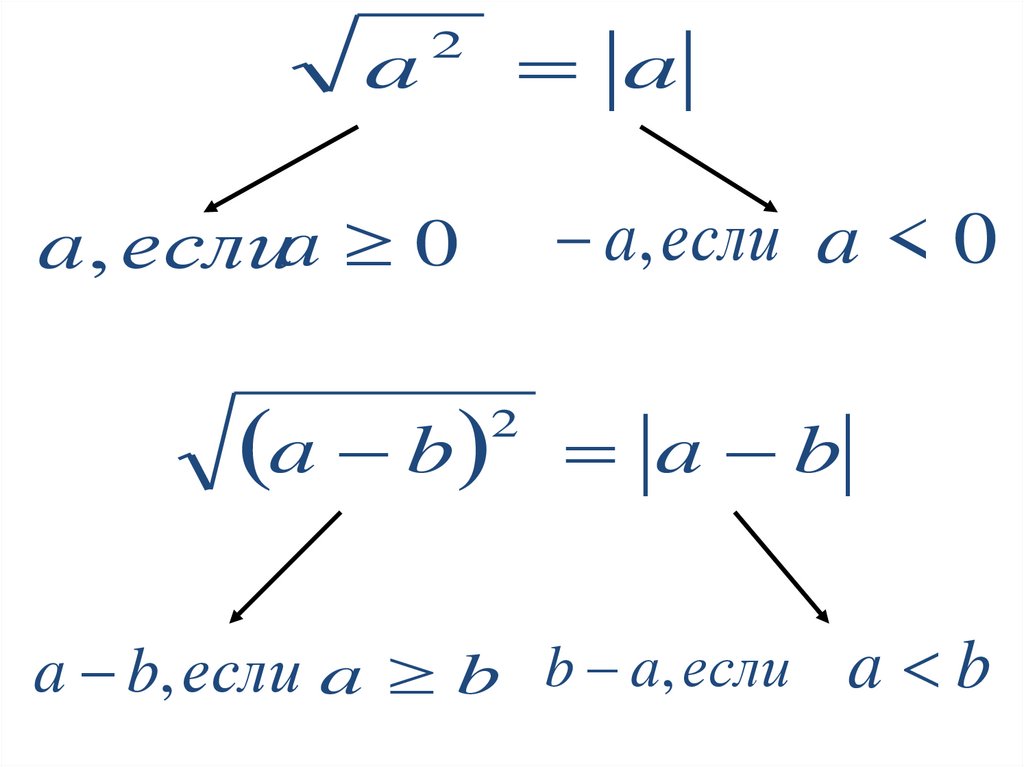




 mathematics
mathematics








