Similar presentations:
Иррациональные уравнения
1.
2. Цель урока:
Познакомиться с понятиемиррациональных уравнений и
рассмотреть методы их решения
3. Из последнего промежутка найти наименьшее положительное целое число.
Найти область определения:Y=
Y=
x 6 ;
X>0
Y=
Y=
X≥6
X > -2
x ;
X≥0
Из последнего промежутка найти
наименьшее положительное целое число.
4. Упростить выражение:
2x ;
5
4
x ;
2
10
x ;
x ;
4
8
x ;
6
12
x ;
3
3
x ;
x ;
3
3
3
9
x .
5.
"НАЙДИ ОШИБКИ"Решение уравнений
1) х 3 8
х = 2
2) х 36
3) х 3 8
1296
-2
х = 6
нет корней
4) 3 х 3
-27
х= 27
Применение формул сокращенного умножения
1) х 2 х 2 + 4 х 4;
2
2) 3 х 2 93 х 2 12 х 4;
2
3) 2 у 4 4 у2 16 у. +16
2
6. Числом какого вида является ?
Является ли число х корнем уравнения:0
X0 =27
X0 = 36
X0=8
2=x²
X0=
Числом какого вида является
?
7. История «неразумных» чисел
Удивительное открытие пифагорийцевКаким числом выражается длина диагонали квадрата со
стороной 1?
С латыни слово «irrationalis» означает «неразумный».
«surdus» - «глухой» или «немой»
«ни высказать, ни выслушать»
8.
34 =64
V=Sосн*H
9. С международным днем числа «пи»
Сегодня в мире отмечается один из самыхнеобычных праздников — Международный
день числа «Пи» (International π Day).
Впервые День был отмечен в 1988 году в
научно-популярном музее Эксплораториум в
Сан-Франциско (San Francisco Exploratorium).
С этим необычным числом мы сталкиваемся
уже в младших классах школы, когда
начинаем изучать круг и окружность. Число π
— математическая константа, выражающая
отношение длины окружности к длине ее
диаметра. В цифровом выражении π
начинается как 3,141592... и имеет
бесконечную математическую
продолжительность.
10.
День Пи празднуют каждый год 14 марта. Эточисло выбрано неспроста - 3,14, где 3 - месяц
март, а 14 - число месяца.
Кроме этого праздника, в этот
день родились многие известные
личности, такие как Эйнштейн,
Скиапарелли (астроном), Сернан
(последний, кто был на Луне).
11. Пи - неизменная и самая распространенная константа в математических вычислениях.
12. Символ, который обозначает Пи, существует более 250 лет. Впервые он появился в 1706 году благодаря Уильяму Джонсу.
британский(валлийский)
математик,
первый
обозначил число
пи греческой
буквой .
Отец филолога
Уильяма Джонса.
13.
Но загадка таинственного числа не разрешенавплоть до сегодняшнего дня, хотя по-прежнему
волнует ученых. Попытки математиков полностью
вычислить всю числовую последовательность часто
приводят к курьезным ситуациям. Например,
математики братья Чудновские в Политехническом
Университете Бруклина специально с этой целью
сконструировали суперскоростной компьютер.
Однако установить рекорд им не удалось – пока
рекорд принадлежит японскому математику
Ясумаса Канада, который смог вычислить 1,2
биллиона чисел бесконечной
последовательности.
14.
Знаете ли вы, что взеркальном отображении
числа 3,14 читается слово
"pie"? В переводе с
английского оно означает
пирог.
15.
Интересно и то, что число Пииспользуют и при вычислении
прогноза погоды.
16.
Занимательно, что пирамидаХеопса является неким
воплощением числа пи в
природе? Так, соотношение
между высотой и периметром
основания дает в результате
число 3,14.
17.
Некоторые специалисты в областистроительства считают, что и
Вавилонская башня и храм Соломона
были построены именно на основании
числа Пи. А рухнули эти сооружения не
по гневу Божьему, а из-за неверных
математических расчетов.
18.
Знаменитая компания Givenchyвыпустила коллекцию духов под
названием Pi.
19.
Теперь ещё интересные факты очисле Пи. Если каждой клавише
музыкального инструмента
присвоить число из ряда числа
Пи, то получается очень
красивая, космическая мелодия.
Прослушать ее вы можете на
этом видео. Вас это впечатлит,
обещаем. Эта мелодия
таинственна и загадочна.
20.
21.
Определение:Уравнения, в которых переменная содержится
под знаком корня, называются
иррациональными.
Выбрать иррациональное уравнение:
22.
Решите уравнение:2х 1 3
2
2
( 2 х 1) 3
2х 1 9
х 4
Проверка:
2 4 1 3
9 3
3 3верно
Ответ:
х 4
23.
Решите уравнение:2х 5 4х 7
( 2х 5) ( 4х 7 )
2х 5 4х 7
х 1 посторонний корень
2
2
Проверка :
2 1 5
4 1 7
3не существует
Ответ : решений нет
24.
Решите уравнение:2х 1 3
2
2
( 2 х 1) 3
2х 1 9
х 4
Проверка:
2 4 1 3
9 3
3 3верно
Ответ:
х 4
25.
Решение иррациональных уравненийМетод возведения в степень:
1) Уединить корни
2) Возвести обе части уравнения в
степень.
3) Решить уравнение
4) Сделать проверку!!!
26.
Решите уравнение:5 х 16 х 2
2
2
( 5 х 16 ) ( х 2)
5х 16 х 4 х 4
2
х 9 х 20 0
2
D 1, х 5, х 4
Проверка :
х 5
Ответ :
х 4
3 3верно 2 2верно
х 5
х 4
27.
1 1(1) ( 1)
2
неверно
2
верно
28.
При возведении обеих частейуравнения
• в четную степень проверка обязательна.
• в нечетную степень проверка не нужна.
29.
Решите уравнение:3
x 12 4
( x 12) 64;
3
3
х 12 64
х 52
30.
Решите уравнение:х 3 1 х 4
2
2
( х 3 ) (1 х 4 )
х 3 1 2 х 4 х 4
2 х 4 0
х 4 0
х 4 0
х 4
31.
Проверка4 3 1 4 4
1 1верно
Ответ :
х 4
32.
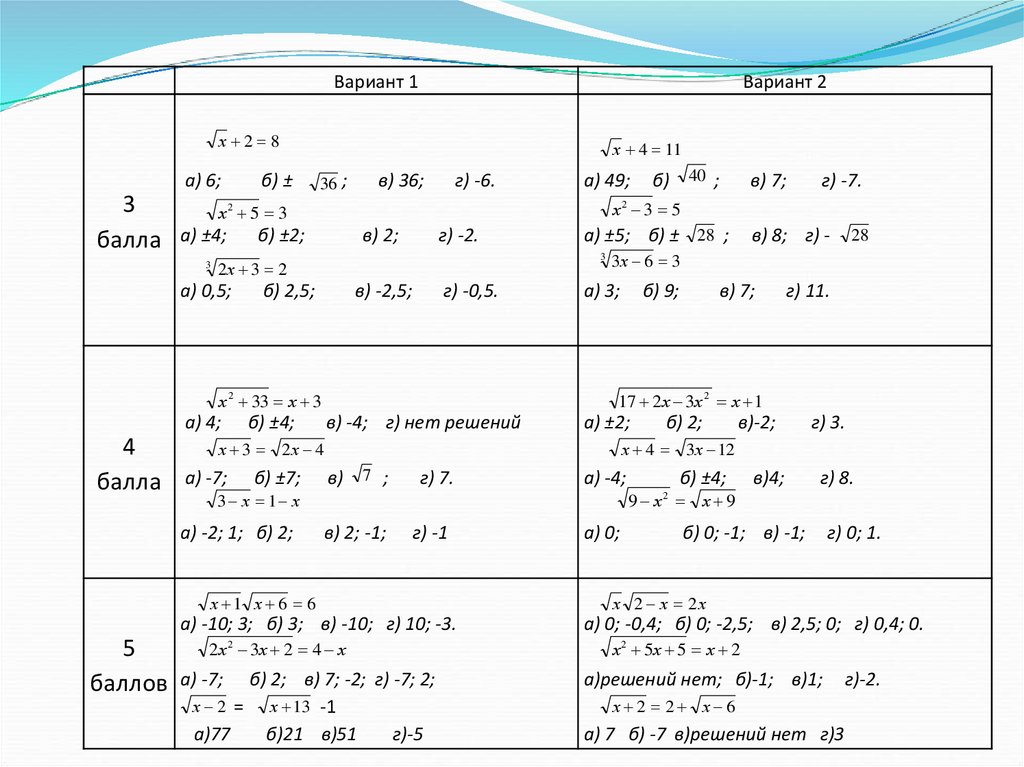
Вариант 1Вариант 2
х 2 8
а) 6;
3
балла
б) ±
х 4 11
36 ;
в) 36;
г) -6.
а) ±4;
б) ±2;
в) 2;
г) -2.
б) 2,5;
в) -2,5;
г) -0,5.
х 2 33 х 3
а) 4;
в) -4; г) нет решений
в) 7 ;
г) 7.
б) 9;
в) 7;
г) 11.
а) ±2;
б) 2;
в)-2;
г) 3.
а) -4;
б) ±4;
в)4;
г) 8.
9 х х 9
2
в) 2; -1;
г) -1
х 1 х 6 6
2 х 2 3х 2 4 х
а) -7;
28
х 4 3х 12
а) -10; 3; б) 3; в) -10; г) 10; -3.
5
баллов
а) 3;
3 х 1 х
а) -2; 1; б) 2;
в) 8; г) -
17 2 х 3х 2 х 1
б) ±4;
б) ±7;
г) -7.
3х 6 3
х 3 2х 4
а) -7;
в) 7;
а) ±5; б) ± 28 ;
3
2х 3 2
а) 0,5;
б) 40 ;
х2 3 5
х2 5 3
3
4
балла
а) 49;
б) 2; в) 7; -2; г) -7; 2;
х 2 =
х 13 -1
а)77
б)21 в)51
г)-5
а) 0;
б) 0; -1; в) -1;
г) 0; 1.
х 2 х 2х
а) 0; -0,4; б) 0; -2,5; в) 2,5; 0; г) 0,4; 0.
х 2 5х 5 х 2
а)решений нет; б)-1; в)1;
х 2 2 х 6
а) 7 б) -7 в)решений нет г)3
г)-2.
33.
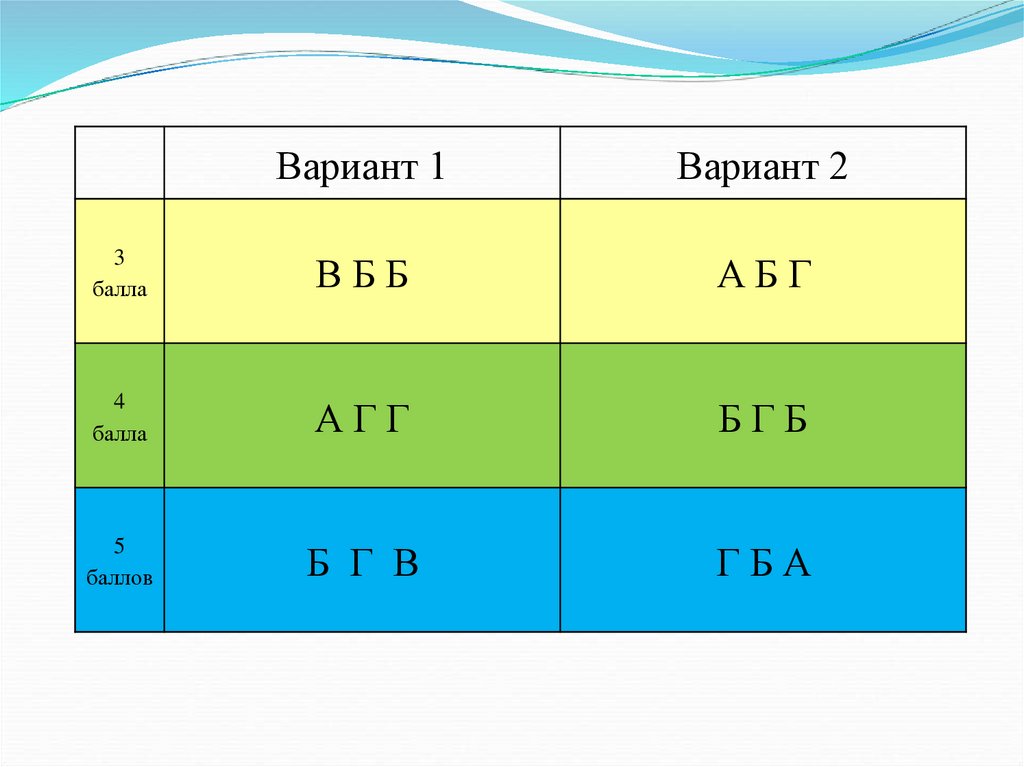
Вариант 1Вариант 2
3
балла
ВББ
АБГ
4
балла
АГГ
БГБ
5
баллов
Б Г В
ГБА

























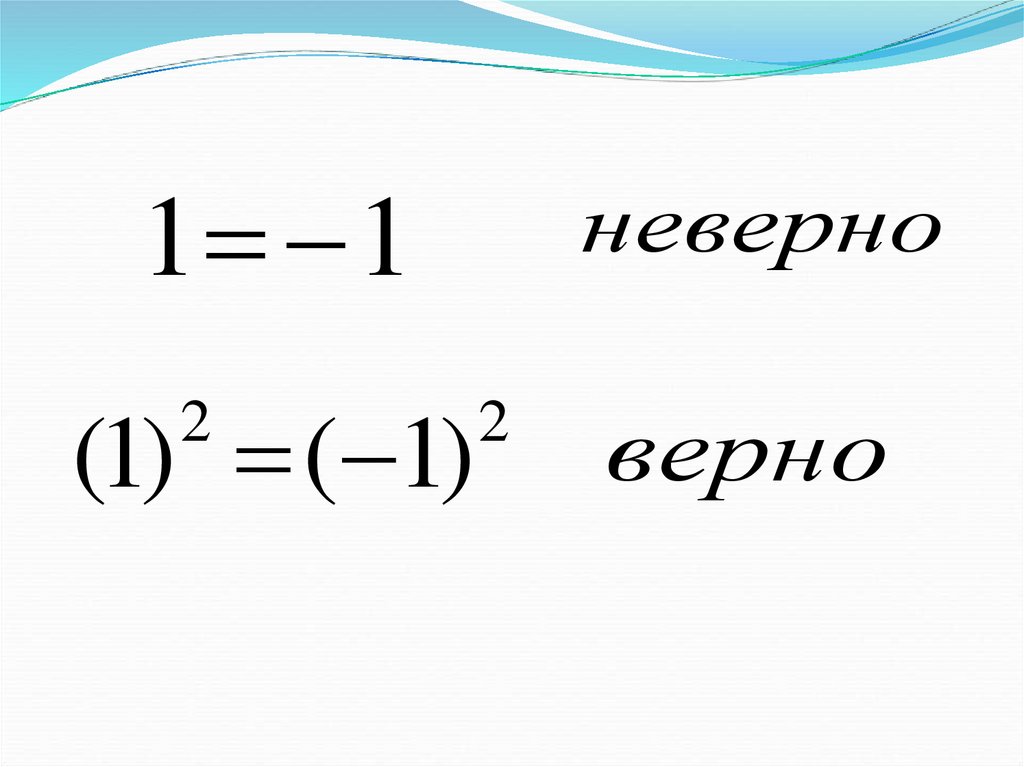




 mathematics
mathematics








