Similar presentations:
Иррациональные уравнения
1.
ИРРАЦИОНАЛЬНЫЕУРАВНЕНИЯ
11.2.2.2. Уметь решать
иррациональные уравнения
методом возведения обеих частей
уравнения в n-ю степень
2.
"НАЙДИ ОШИБКИ"Решение уравнений
1) х 3 8
х = 2
2) х 36
х = 6
3) х 3 8
4) 3 х 3
нет корней
х= 27
Применение формул сокращенного умножения
1) х 2 х 2 4 х 4;
2
2) 3 х 2 3 х 2 12 х 4;
2
3) 2 у 4 4 у 16 у.
2
3.
Правильно найденные ошибки отметьте «+» и в листе самоконтроля, встолбец «После проверки», внесите число, соответствующее количеству
«+» и поставьте свою подпись.
"НАЙДИ ОШИБКИ"
Решение уравнений
1) х 3 8
х=2
2)
х 36
3) х 3 8
х 2
х = 362
4)
3
х 3
х= -27
Применение формул сокращенного умножения
1) х 2 х 4 х 4;
2
2
2) 3 х 2 9 х 2 12 х 4;
2
3) 2 у 4 4 у 2 16 у 16.
2
4.
ПОВТОРИМУравнение, содержащее неизвестную под
знаком радикала, а также под знаком
возведения в дробную степень
?
называют иррациональным.
5.
а) 2 х 7 9;б) 3х+5 2;
в ) 2 х = 3х + 4;
г ) 3х+5 2;
д) х + 6х +2 =0;
е) 2 х 7 9.
3
2
1)
2)
3
Какие из уравнений не являются иррациональными?
Какие иррациональные уравнения не имеют корней?
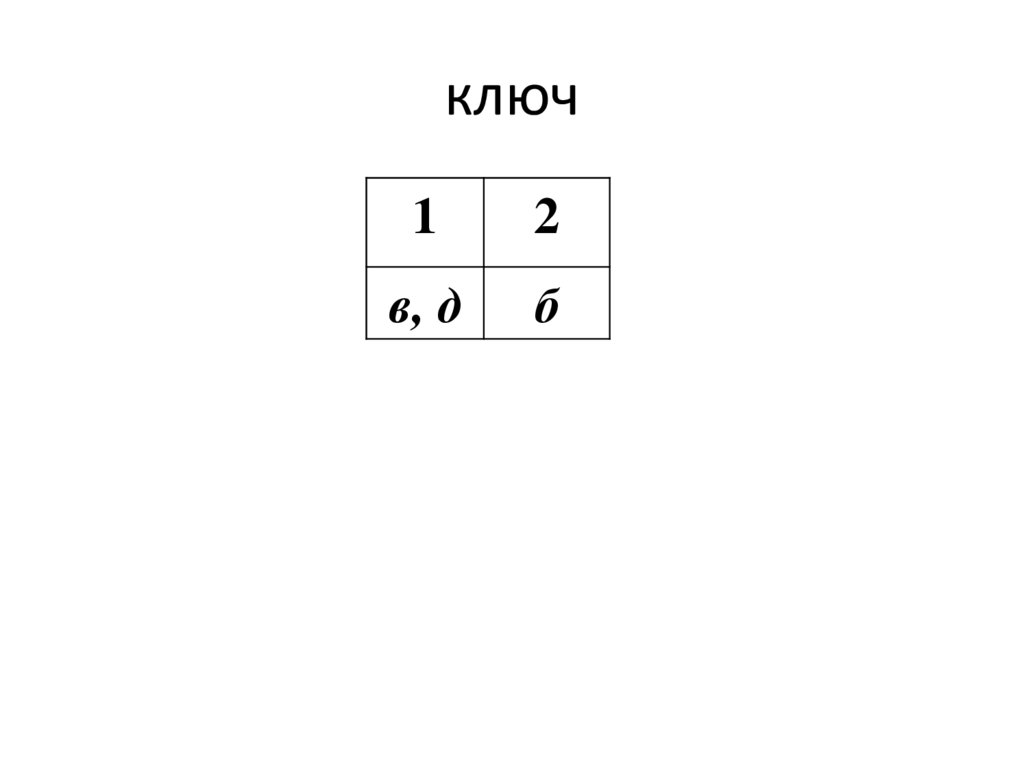
6.
ключ1
2
в, д
б
7.
Основная цель при решении иррациональных уравненийсостоит в том, чтобы освободиться от знака радикала и
получить рациональное уравнение.
• При решении иррациональных уравнений применяют
следующие основные методы:
• возведение в степень обеих частей уравнения;
• введение новой переменной;
• разложение на множители.
Кроме основных методов следует рассмотреть дополнительные
методы решения иррациональных уравнений:
• умножение на сопряженное;
• переход к уравнению с модулем;
• метод «пристального взгляда» (метод анализа уравнения);
• использование монотонности функции.
8.
Иррациональные уравнения содержат радикалы.Чтобы избавиться от радикалов, необходимо
возвести обе части уравнения в одну и ту же
степень с натуральным показателем.
Если:
Возводим в нечетную степень, то получаем
равносильное уравнение;
Возводим в четную степень –получаем
уравнение -следствие, поэтому можем
получить посторонние корни. В этом случае
делаем проверку.
9.
10.
11.
12.
Решим совместными усилиями иррациональноеуравнение:
x 12 x 0.
Решение:
Уединим радикал :
x 12 x.
Возведем обе части уравнения в квадрат:
Решим полученное уравнение:
x 2 x 12 0.
Проверка: 3 :
Ответ:
4
3 12 ( 3) 0,
√4+3= 0
5=0 – не
верно, т.е. -3
посторонний
корень
x 12
2
x2.
Тогда D = 49, х = -3, х = 4.
4:
4 12 4 0,
16 4 0,
4 – 4 = 0;
0 = 0 - верно,
13.
Решим совместными усилиями иррациональноеуравнение: 7 x 5 2 0.
Решение:
Уединим радикал :
7
x 5 2.
Возведем обе части уравнения в 7 степень:
Решим полученное уравнение:
x 128 5,
x 133.
Ответ:
-133
x 5 128.
14.
15.
Найдите корень уравнения:х
3
4
34 2 х
24
5
6
2х
3
х32
3
5
2х2ххх16
13
02
5
х
3
2
3
7533
Правильный ответ:
6,5
125
31
48
0,5
25
0327
81
16.
Работа в группах17.
Работа в группах18.
Работа в группах19.
• Работа по учебнику:• Стр 116
№ 14.3 (1 ст)
20.
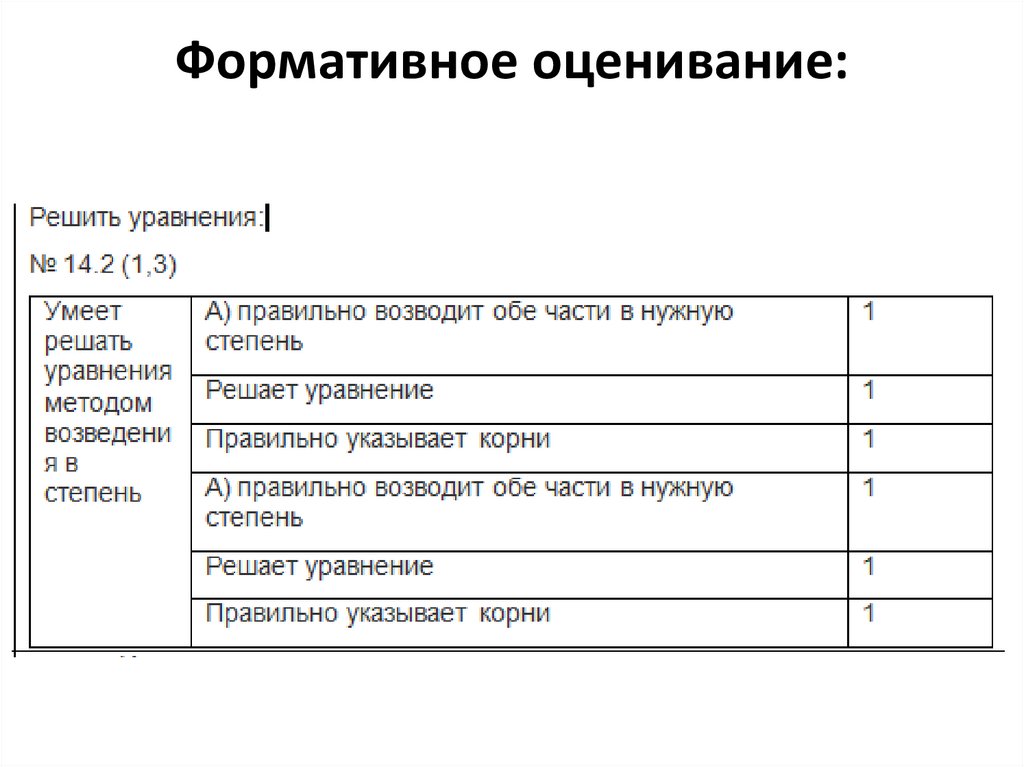
Формативное оценивание:21.
Домашнее задание :• п.14 № 14.3(2ст) №14.14.6(1)



















 mathematics
mathematics








