Similar presentations:
Решение иррациональных уравнений и их систем
1.
Решениеиррациональных
уравнений и их
систем
2.
Цели обучения11.2.2.1 - знать определение
иррационального уравнения, уметь
определять его область допустимых
значений;
11.2.2.2 - уметь решать иррациональные
уравнения методом возведения обеих частей
уравнения в n-ю степень;
11.2.2.3 - уметь решать иррациональные
уравнения методом замены переменной;
11.2.2.4 - уметь решать системы
иррациональных уравнений;
3. Критерии успеха
Учащийся достиг цели обучения, если– знает определение иррационального уравнения
– обосновывает методы решения иррациональных
уравнений (неравенств)
– проводит равносильные преобразования
– проверяет корни
– использует определение иррациональных уравнений
(неравенств)
– применяет методы решения иррациональных уравнений
(неравенств)
– обосновывает дополнительные методы решения
иррациональных уравнений (неравенств)
– отделяет корни уравнения от посторонних корней
4.
Определение. Иррациональнымуравнением называется уравнение,
содержащее неизвестную под знаком
радикала, а также под знаком возведения
в дробную степень.
Например:
2x 3 x 1
3
x 5 12 x 4 5
4
7
3 x x 8 15
5.
Решите уравненияkx b c в зависимости от с.
Приведите примеры.
6.
1. Уравнения видаf ( x) c.
а) если с<0 уравнение не имеет корней;
б) если с=0, то данное иррациональное
уравнение равносильно уравнению: f(x)=0;
в) если с>0, то данное иррациональное уравнение
равносильно следующей системе:
f ( x) 0,
2
f ( x) с .
7.
Решите уравнения:Пример 1.
Пример 2.
Пример 3.
х 2 2 х 9 3
х х 2 0
2
х 2 5х 10 2
8.
2. Уравнения видаf ( x) g ( x).
Данное иррациональное уравнение равносильно системе:
f ( x ) 0,
g ( x ) 0,
f ( x ) g ( x ).
Пример 4.
Решите уравнение:
9 х 2 3х 6 6 х 24
9.
Основные методы решенияиррациональных уравнений:
возведение в степень обеих частей
уравнения;
введение новой переменной;
разложение на множители.
10.
Дополнительныеметоды решения иррациональных
уравнений:
умножение на сопряженное;
переход к уравнению с модулем;
метод «пристального взгляда»
(метод анализа уравнения);
использование монотонности
функции.
11.
Метод возведения в степеньобеих частей уравнения:
1) Если иррациональное уравнение содержит только
один радикал, то нужно записать так, чтобы в одной
части знака равенства оказался только этот радикал.
Затем обе части уравнения возводят в одну и ту же
степень, чтобы получилась рациональное уравнение.
2) Если в иррациональном уравнении содержится два или
более радикала, то сначала изолируется один из
радикалов, затем обе части уравнения возводят в одну и
ту же степень, и повторяют операцию возведения в
степень до тех пор, пока не получится рациональное
уравнение.
Если:
возводим в нечетную степень, то получаем равносильное
уравнение;
возводим в четную степень, то можем получить посторонние
корни. В этом случае делаем проверку.
12.
f ( x) g ( x)f ( x) g ( x)
f ( x) g ( x)
f ( x ) 0 ( g ( x ) 0)
f ( x) g ( x)
2
g ( x) 0
13.
Решите уравнение:1) х 2 2 х
14.
Решите уравнение:2) 3 х 2 х
15.
Решите уравнение:3) 2 х 3 4 х
16.
Решите уравнение:4) х 2 5х 1 2 х 1
17.
Решите уравнение:5) х 1 3 х 2 х 1
18.
Решите уравнение:7) 3 5 х 3 х 5 1
19.
Метод введения новой переменнойДанный метод применяется в том случае,
когда в уравнении неоднократно
встречается некоторое выражение,
зависящее от неизвестной величины.
Тогда имеет смысл принять это выражение
за новую переменную и решить уравнение
сначала относительно введенной
неизвестной, а потом найти исходную
величину.
20.
Решите уравнение:8) 4 х 8 х 2 0











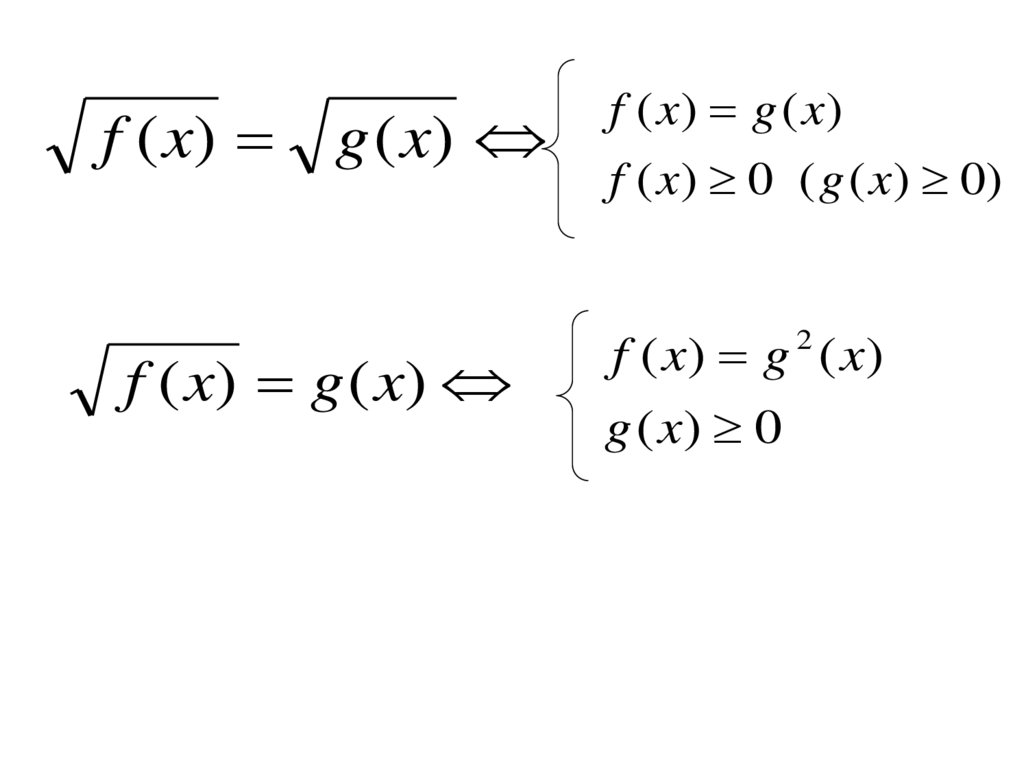










 mathematics
mathematics








