Similar presentations:
Иррациональные уравнения. Решение иррациональных уравнений
1.
Решениеиррациональных
уравнений
2.
Цели обучения11.2.2.1 - знать определение
иррационального уравнения, уметь
определять его область допустимых
значений;
11.2.2.2 - уметь решать иррациональные
уравнения методом возведения обеих частей
уравнения в n-ю степень;
11.2.2.3 - уметь решать иррациональные
уравнения методом замены переменной;
11.2.2.4 - уметь решать системы
иррациональных уравнений;
3. Критерии успеха
Учащийся достиг цели обучения, если– знает определение иррационального уравнения
– обосновывает методы решения иррациональных
уравнений (неравенств)
– проводит равносильные преобразования
– проверяет корни
– использует определение иррациональных уравнений
(неравенств)
– применяет методы решения иррациональных уравнений
(неравенств)
– обосновывает дополнительные методы решения
иррациональных уравнений (неравенств)
– отделяет корни уравнения от посторонних корней
4.
Home work5.
Home work6.
Найдите сумму корней уравнения:9) х 4 х 1 3 х 2 5 х 2 6
7.
Решите уравнение:2х 1
х 1
10)
2
1
х 1
2х 1
8.
Метод разложения на множителиДля решения иррациональных уравнений данным методом следует
пользоваться правилом:
произведение равно нулю тогда и только тогда, когда хотя бы
один из множителей, входящих в произведение, равен нулю; а
остальные при этом имеют смысл.
Уравнение
f ( x) q( x) 0
равносильно совокупности
q( x) 0
f ( x) 0
1)
q ( x) определена
2)
f ( x) 0
9.
Решите уравнение:11) х 5х 6
2
х 2
0
х 5
Ответ: -2; 6
10.
Решите уравнение:12) х 3 х 2 4 х 3
Ответ: 3






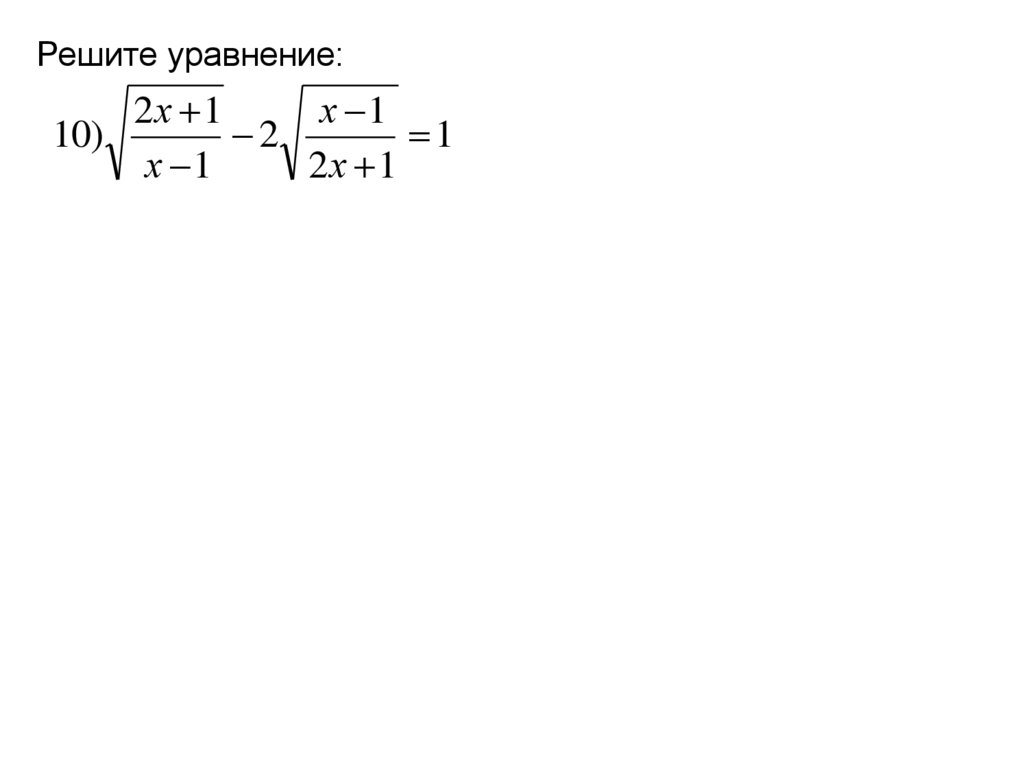






 mathematics
mathematics








