Similar presentations:
Сложное движение точки ускорение кориолиса
1.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИУСКОРЕНИЕ КОРИОЛИСА
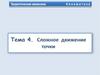
Как следует из определения Wкор 2 Vотн ,
Vотн
Модуль:
вектор ускорения Кориолиса перпендикулярен плоскости, содержащей вектор угловой скорости
подвижной системы отсчёта и
вектор относительной скорости
точки, причём направлен в ту
сторону,
откуда
кратчайший
Wкор
поворот от вектора
угловой
скорости к вектору относительной скорости виден против хода
часовой стрелки.
Wкор 2 Vотн sin
2.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИУСКОРЕНИЕ КОРИОЛИСА
Как следует из определения Wкор 2 Vотн ,
Vотн
Модуль:
ускорения
вектор
Кориолиса перWкор 2 плоскости,
Vотн sin
пендикулярен
содержащей вектор угловой скорости
подвижной системы отсчёта и
вектор относительной скорости
точки, причём направлен в ту
сторону,
откуда
кратчайший
Wкор
поворот от вектора
угловой
скорости к вектору относительной скорости виден против хода
часовой стрелки.
Wкор 2 Vотн sin
3.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИУСКОРЕНИЕ КОРИОЛИСА
Wкор 2 Vотн ,
Wкор 2 Vотн sin
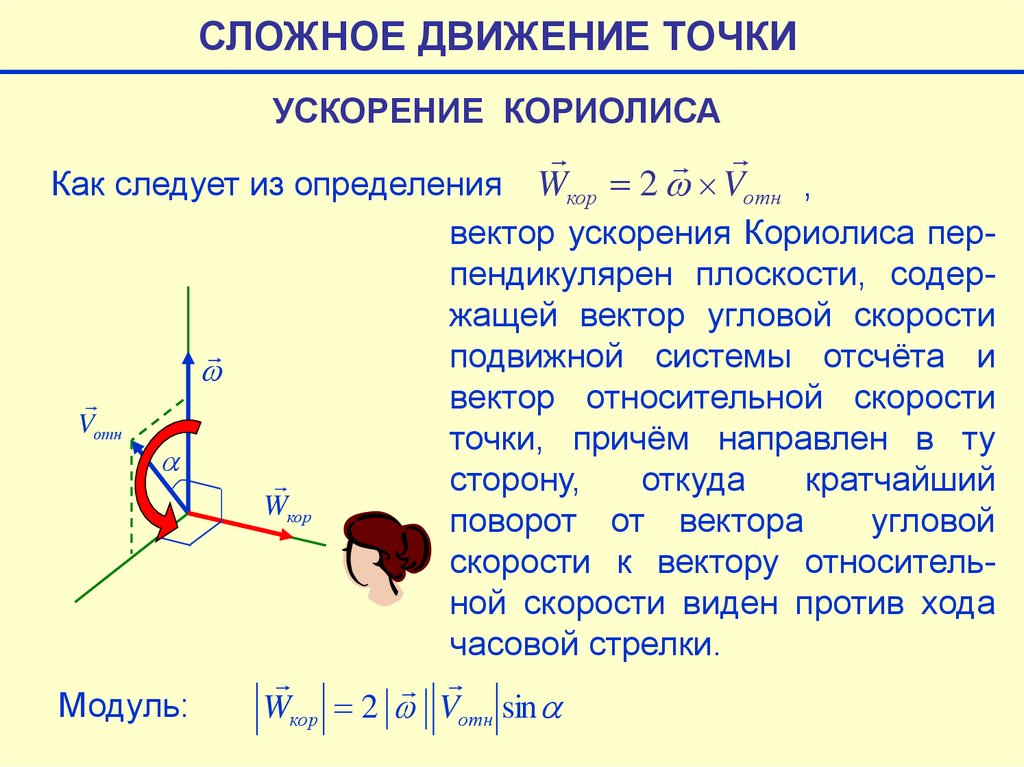
Для определения направления ускорения Кориолиса во многих случаях удобно
использовать правило Жуковского:
Vотн
Wкор
для определения направления ускорения Кориолиса необходимо проекцию вектора относительной скорости на плоскость, перпендикулярную
вектору угловой скорости подвижной
системы отсчёта, повернуть в
сторону вращения на прямой угол
4.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИУСКОРЕНИЕ КОРИОЛИСА
Wкор 2 Vотн ,
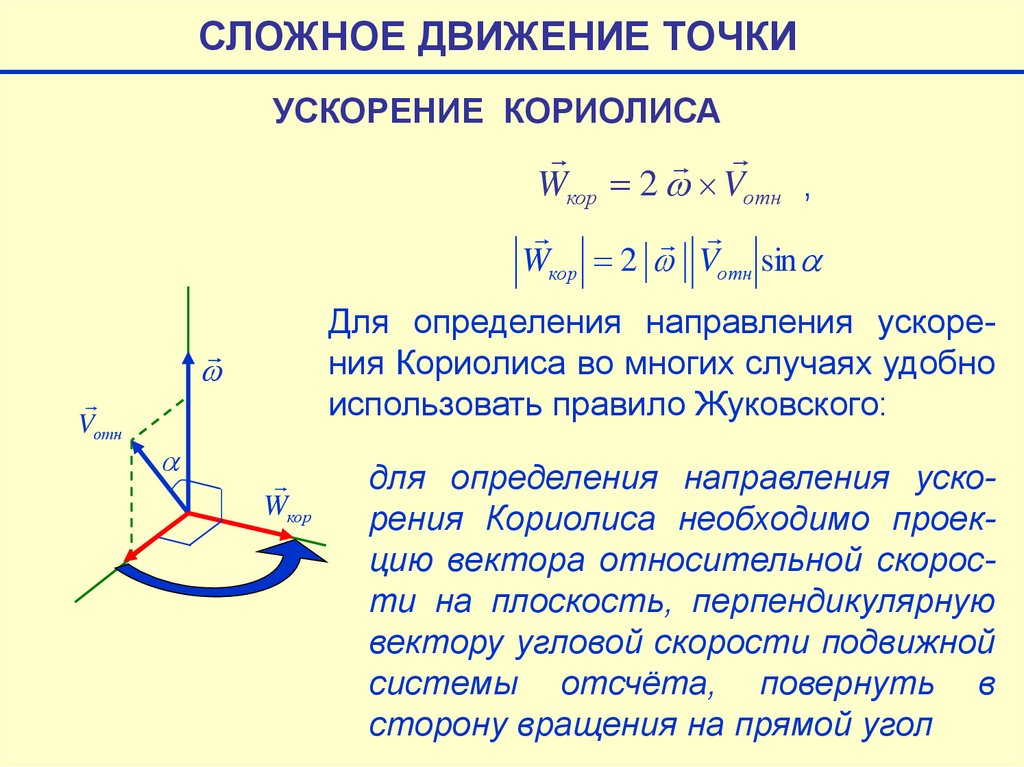
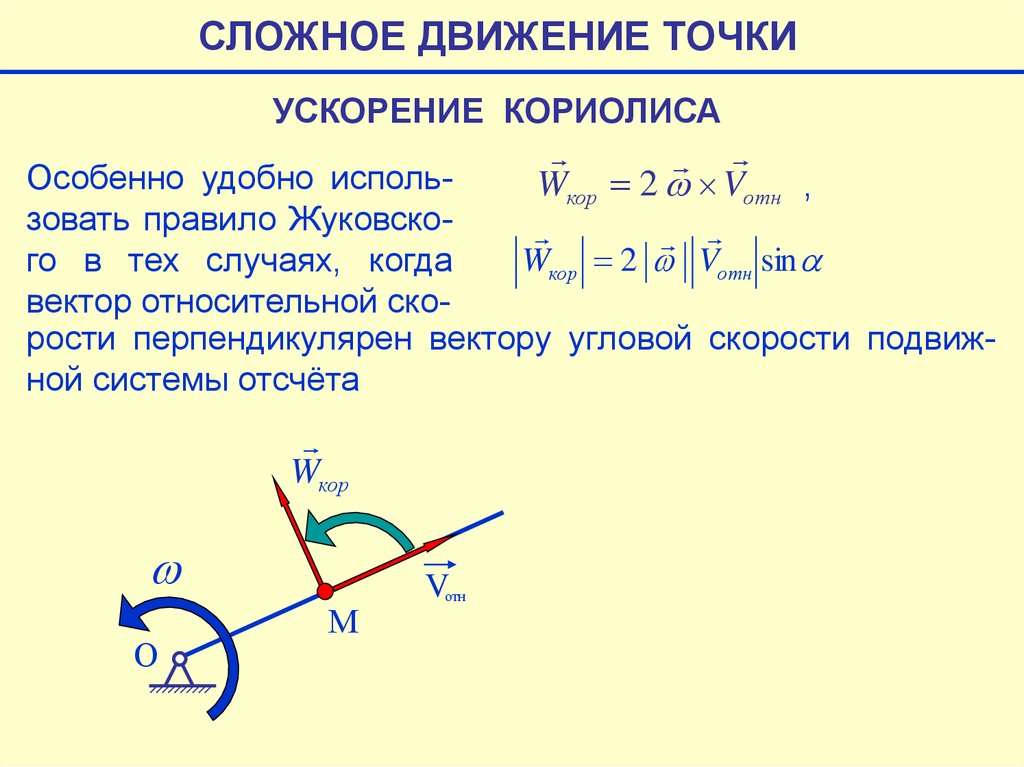
Особенно удобно использовать правило Жуковско
Wкор 2 Vотн sin
го в тех случаях, когда
вектор относительной скорости перпендикулярен вектору угловой скорости подвижной системы отсчёта
Wкор
О
М
Vотн
5.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИУСКОРЕНИЕ КОРИОЛИСА
Wкор 2 Vотн ,
Особенно удобно использовать правило Жуковско
Wкор 2 Vотн sin
го в тех случаях, когда
вектор относительной скорости перпендикулярен вектору угловой скорости подвижной системы отсчёта
Wкор
О
М
Vотн
6.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИУСКОРЕНИЕ КОРИОЛИСА
Wкор 2 Vотн ,
Wкор 2 Vотн sin
Отметим случаи обращения в нуль ускорения Кориолиса:
1. 0, т.е. подвижная система отсчёта движется
поступательно;
2. Вектор угловой скорости подвижной системы
отсчёта коллинеарен вектору относительной
скорости точки;
3. В моменты времени, когда относительная
скорость точки обращается в нуль.
7.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИУСКОРЕНИЕ КОРИОЛИСА
Wкор 2 Vотн ,
Wкор 2 Vотн sin
Отметим случаи обращения в нуль ускорения Кориолиса:
1. 0, т.е. подвижная система отсчёта движется
поступательно;
2. Вектор угловой скорости подвижной системы
отсчёта коллинеарен вектору относительной
скорости точки;
3. В моменты времени, когда относительная
скорость точки обращается в нуль.



 physics
physics