Similar presentations:
Сложное движение. Ускорение Кориолиса (лекция 13)
1. Сложное движение. Ускорение Кориолиса
12.
Что есть неинерциальная система отсчета?Система отсчета является неинерциальной, если она
движется ускоренно по отношению к инерциальной
система.
Ускоренное движение системы отсчета подразумевает
ускоренное (относительно инерциальной системы)
движение всех измерительных приборов и
конструкций, относящихся к ускоренно движущейся
системе: линеек, часов, пружин, системы координат.
2
3.
Согласно преобразованиям Галилея, тело, покоящеесяили движущееся по инерции (без ускорения) в
инерциальной системе отсчета, движется ускоренно в
неинерциальной системе: a 0 . Согласно второму
закону Ньютона, движение по инерции равносильно
отсутствию (равнодействующей) сил взаимодействия:
Fвз 0
Следовательно, в неинерциальной системе ускорение
не пропорционально равнодействующей сил
взаимодействия:
a Fвз / m
Отсюда возникает вопрос о построении динамической
модели движения в неинерциальной системе.
3
4.
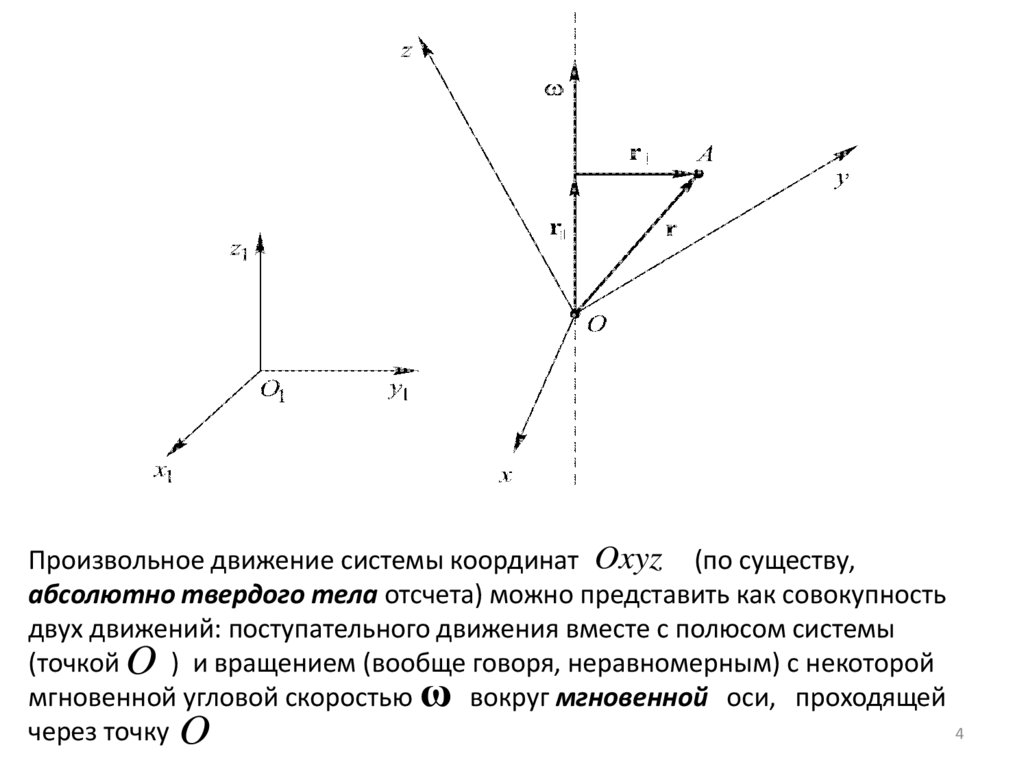
Произвольное движение системы координат Oxyz (по существу,абсолютно твердого тела отсчета) можно представить как совокупность
двух движений: поступательного движения вместе с полюсом системы
(точкой O ) и вращением (вообще говоря, неравномерным) с некоторой
мгновенной угловой скоростью ω вокруг мгновенной оси, проходящей
4
через точку O
5.
Производная по времени вращающегося вектора неизменнойдлины
dA d A sin
dA d
A sin A sin ω, A
dt
dt
dA
ω, A
dt
ˆ
dx
de x
ˆ , e x
dt dt , x
ˆ
dy
de y
ˆ , e y
, y
dt
dt
dzˆ
de z
dt dt , zˆ , e z
5
6.
dxe x + ye y + ze z ) =
(
dt
dx
dy
dz
= ex
+ ey
+ e z + [ω,r ]= v + [ω,r ]
dt
dt
dt
d
v xe x + v y e y + v z e z ) =
(
dt
dv y
dv x
dv z
= ex
+ ey
+ ez
+ [ω, v ]= a + [ω, v ]
dt
dt
dt
6
7.
Кинематическая связь между скоростями в двух системахотсчета
riner r0 r;
dr1 dr0 dr
viner
dt
dt dt
v V0 [ω, r ] v VS
Vs V0 [ω, r]
Классическое правило сложения скоростей:
Скорость материальной точки в системе К1 является суммой
скоростей этой точки в системе К и скорости точки
пространства, вмороженного в систему К.
7
8.
Кинематическая связь между ускорениями в двух системахотсчета
dv dV0 d
ainer
ω, r
dt
dt dt
dV0
dv
ω, v
β, r ω, v ω, ω, r
dt
dt
a ω, v a 0 β, r ω, v ω, ω, r
a a 0 2 ω, v ω, ω, r β, r
ainer a a S
a S a0 2 ω, v ω, ω, r β, r
8
9.
Второй закон Ньютона в инерциальной системе K1ma1 Fвз
ma m(a1 as ) ma1 mas Fвз mas F
F Fвз mas Fвз Fинерции
Fинерции mas ma0 2m[ v, ω] m[ω,[ω, r]] m[β, r]
Основной закон динамики материальной точки в неинерциальной системе K
ma F Fвз Fинерции
1
1
1
a F Fвз Fинерции
m
m
m
Основной закон динамики в неинерциальной системе имеет тот же
вид, что и в инерциальной системе, однако в неинерциальной системе
появляются новые силы – силы инерции. Возникновение этих сил
полностью обусловлено неинерциальностью системы отсчета – ее
9
ускоренным движением относительно инерциальной системы.
10.
Реальность – ирреальность сил инерцииТермин «силы инерции» - калька с французского. Эквивалентный немецкий термин «мнимая» или «фиктивная» сила, а эквивалентный английский
термин –
«псевдосила». Эти определения отражают двойственную природу сил инерции.
Реальность: Наличие любых сил физически проявляется только в их
способности создавать ускорения и/или растягивать пружины.
Силы инерции растягивают неподвижные относительно неинерциальной
системы
пружины
(например,
прикрепленные
к
стенкам
ускоряющегося/тормозящего вагона) и создают ускорения в этой системе. Эти
силы реально ощущаются аппаратурой, встроенной природой в живые
существа.
Ирреальность: Силы инерции не обусловлены взаимодействием тел, они
изменяются при переходе в системы отсчета, движущиеся ускоренно
относительно друг друга, в инерциальных системах они исчезают.
Природа сил взаимодействия не ясна. Гипотеза ОТО: силы инерции, так же как
и гравитационные силы, возникают в результате искривления пространства
большими массами (принцип эквивалентности).
10
11.
Классификация сил инерции.Классификация сил инерции производится в соответствие с классификацией
составляющих переносного ускорения a s
as a0 2[ω, v] [ω,[ω, r]] [β, r]
1. a 0 ускорение поступательного движения неинерциальной системы K
2.
aос [ω,[ω, r]] ускорение вращательного движения осей системы K осестремительное ускорение
r = r + r
разложение радиус вектора на параллельную и перпендикулярную
составляющие относительно мгновенной оси вращения
aос [ω,[ω, r ]] [ω,[ω, r ]] ω(ω,r ) r (ω,ω) r 2
3. a K 2[ω, v] ускорение, обусловленное относительным движением
материальной точки во вращающейся системе – ускорение Кориолиса. Кориолисово
ускорение ортогонально скорости и потому изменяет только направление
движения тела в неинерциальной системе.
4. [β, r ] ускорение, обусловленное неравномерностью вращения
неинерциальной системы
11
12. Классификация составляющих переносного ускорения
Названиеускорения
Ускорение
поступательного
движения
системы
Осестремитель
ное ускорение
Кориолисово
ускорение
Ускорение
неравномерного
вращения
системы
Формула
ускорения
Основные характеристики
ускорения
Влияние на
движение тела в
неинерциальной
системе
Ускорение одинаково во всех
точках системы
Может изменить как
величину скорости,
так и ее направление
Направлено по
перпендикуляру к оси
aос [ω,[ω, r]] вращения, пропорционально
квадрату мгновенной угловой
r 2
скорости
Может изменить как
величину скорости,
так и ее направление
dVO
a0
dt
a K 2[ω, v]
[β , r ]
Ортогонально скорости
движения тела в
неинерциальной системе
Может изменить
только направление
скорости
относительного
движения
Возникает при ускоренной
вращении осей
неинерциальной системы
12
13. Классификация сил инерции.
НазваниеПоступательная
сила инерции
Центробежная
сила инерции
Формула
Основные
характеристики
Действует одинаково в
любых точках системы
F0 ma0
Fц.б. mr
Направлено по
перпендикуляру от оси
2
вращения,
пропорционально
квадрату мгновенной
угловой скорости
Сила Кориолиса
(кориолисова
сила)
FK 2m[ v, ω]
Сила инерции
неравномерного
вращения
F m[β, r ]
Ортогональна скорости
движения тела в
неинерциальной системе
Влияние на движение
в неинерциальной
системе
Может изменить как
величину скорости,
так и ее направление
Может изменить как
величину скорости,
так и ее направление
Искривляет
траекторию вправо по
ходу движения
13
14.
Общие свойства сил инерции.Из последнего свойства следует, что под действием сил
инерции в рамках данной неинерциальной системе
отчета все тела приобретают одинаковые ускорения
14
15.
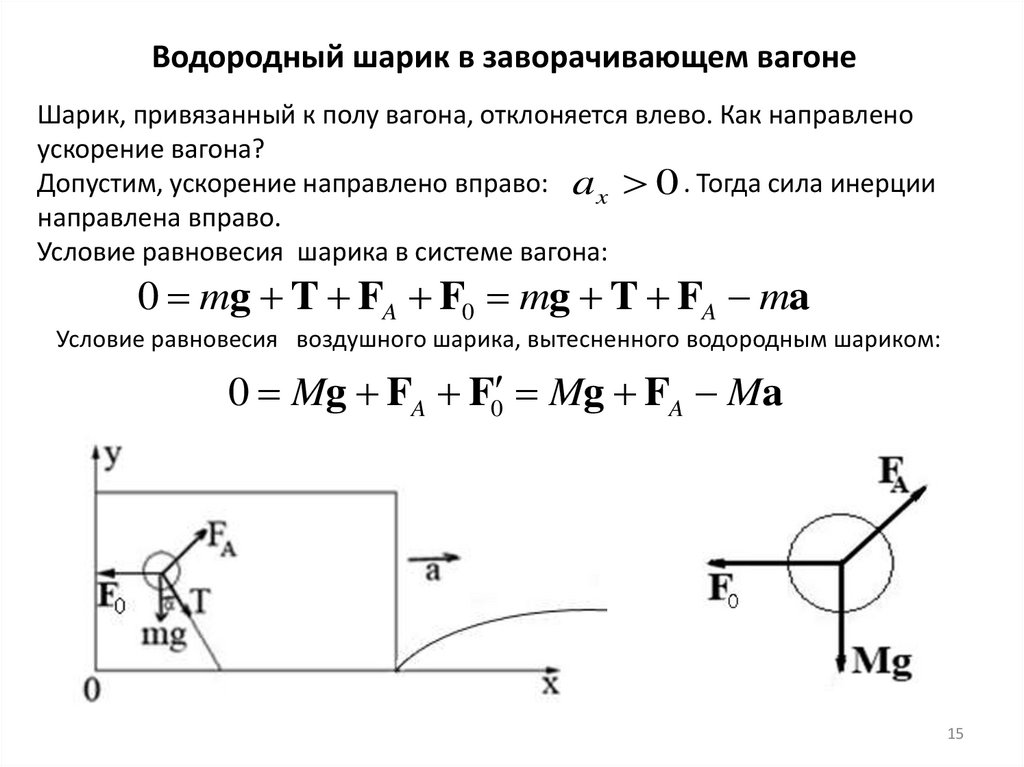
Водородный шарик в заворачивающем вагонеШарик, привязанный к полу вагона, отклоняется влево. Как направлено
ускорение вагона?
Допустим, ускорение направлено вправо: a x 0 . Тогда сила инерции
направлена вправо.
Условие равновесия шарика в системе вагона:
0 mg T FA F0 mg T FA ma
Условие равновесия воздушного шарика, вытесненного водородным шариком:
0 Mg FA F0 Mg FA Ma
15
16.
Из расположения сил следует, что сила Архимеда отклоняется отвертикали в направлении ускорения и ее горизонтальная составляющая
уравновешивает силу инерции
FAx F0 Ma
Вычитая динамические уравнения двух шариков, исключаем Архимедову
силу и приходим к уравнению
0 M m g M m a T M m (g a)
В проекциях на горизонтальную
Ox и вертикальную Oy оси
Tx T sin M m a;
Ty T cos M m g
Tx
a
tg a ax gtg 0
Ty
g
Приходим к противоречию. Следовательно, исходная предпосылка о
направлении ускорения вагона была неправильной: ускорение вагона
направлено влево.
16
17.
Правильное направление сил и ускорения17
18.
Решение задачи в инерциальной (геоцентрической) системеотсчета
ma mg T FA
Ma Mg FA
T M m g m M a M m (g a)
18
19. Центробежная сила
1920.
Центробежная сила, действующая на тело вблизи поверхностиЗемли
Центробежная сила, действующая на тело вблизи поверхности Земли,
обусловлена суточным вращением Земли вокруг своей оси и направлена
ортогонально Земной оси
Fцб m 2r m 2 RЗ cos
Силы, действующие в геоцентрической
системе на неподвижное тело,
расположенное вблизи поверхности Земли
F = Fгр + Fцб mg0 m 2r mg
M m
g 0 G З2
RЗ
g g 0 r
2
Центробежная сила изменяет положения отвеса
и величину ускорения свободного падения.
Поскольку величина центробежной силы меняется при
перемещении по поверхности Земли от экватора к полюсу,
направление и модуль ускорения свободного падения g
зависят от широты местности
, на которой находится тело
20
21.
Расчет угла отклонения от отвеса в модели шарообразной Земли2 RЗ
m 2 r
sin
sin
sin 2
mg
2g
На экваторе
0
g экв g min 9, 780 м / с 2 ;
g 0 g экв
0, 003 0,3%
g0
На полюсах 0,
/ 2, Fцб 0
2
g
g
9,810
м
/
с
Для шарообразной Земли
пол
0
2
g
9,832
м
/
с
Экспериментальные измерения пол
Это различие обусловлено тем, что Земля сплюснутое вдоль полюсов.
g пол g экв 0, 05
0,5%
g0
10
21
22.
Сила КориолисаFK maK 2m v, ω
Влиянием силы Кориолиса объясняется
отклонение к востоку свободно падающих
тел, размывов правых берегов текущих к
северу широких сибирских рек и другие
эффекты.
Сила бокового давления на рельсы поезда,
идущего по меридиану с севера на юг. Эта
сила
обусловлена
дополнительным
давлением поезда на рельсы, возникающим
в результате действия на поезд силы
Кориолиса
F 2m v, ω 2mv sin( ) 2mv sin
ω угловая скорость суточного вращения Земли. Сила бокового
давления, действующая на поезд со стороны рельс, уравновешивает
силу Кориолиса.
22
23.
Если тело движется в плоскости экватора с запада на восток,то сила Кориолиса направлена вертикально вверх, при
движении тела с востока на запад она направлена
вертикально вниз.
23
24.
При движении тел на Земле проявление кориолисовых сил неочень заметно, поскольку в обычных условиях малы и скорости
движения тел, и угловая скорость вращения Земли. Однако
малая сила, которая действует продолжительное время, может
создать довольно ощутимый эффект.
Продолжительное действие кориолисовых сил объясняет тот
факт, что правый берег рек в северном полушарии всегда
более крутой, чем левый, в южном полушарии более крутой—
левый берег (закон Бера). Сила Кориолиса прижимает воду к
правому берегу, и она подмывает его. Поскольку сила Кориолиса
в северном полушарии всегда направлена в правую сторону от
движения тела, то этим и объясняется преждевременный
износ правого рельса на двухколейной железной дороге.
24
25.
Большую роль играют кориолисовы силы в метеорологическихявлениях. Так, отклоняющее влияние кориолисовой силы
заставляет
мощное
океаническое течение
Гольфстрим,
выходящее из Мексиканского залива через Флоридский пролив
в направлении, близком к меридианному, отойти от берегов
Америки, пересечь Атлантический океан и выйти в Баренцево
море у берегов Скандинавии.
Действием кориолисовых сил объясняется направление ветровпассатов.
25
26.
Маятник Фуко – тяжелое тело на длинном подвесе,совершающее малые колебания.
Под действием силы Кориолиса плоскость качаний маятника поворачивается
в том же направлении, в котором движется по небосводу Солнце
Реальный опыт был
произведен ЖаномБернаром Фуко в
Парижской
обсерватории в 1850
году и повторен в
1851 году в
Пантеоне. Маятник
имел длину 67 м и
состоял из
металлического шара
массой m=28 кг.
Маятник Фуко в Парижском Пантеоне
26
27.
Модель маятника Фуко,расположенного в Южном
полушарии.
Изображенная
на
анимации
траектория
движения соответствует
случаю, когда маятник
приводится в движение
коротким толчком из
положения равновесия.
27
28.
Опыт с маятником Фуко поводитсяна полюсе Земли, где направление
отвеса совпадает с осью земного
вращения.
В любой инерциальной системе
отсчета, содержащей ось вращения
Земли, маятник колеблется в одной
плоскости. Но Земля вращается
вокруг этой плоскости с угловой
скоростью ω . Следовательно,
относительно Земли плоскость
качаний маятника вращается в
противоположную сторону с такой
же по величине скоростью
28
29.
Опыт проводится в точке земной поверхности с географическойширотой
ω ωв ωг , ωг ω ω .
29
30.
Динамическое уравнение движения маятника вгеоцентрической системе отсчета
ma FG FK T mg 2m[ v, ω] T
FK 2m[ v, ωв ] 2m[ v, ωг ]
FK(г ) 2m[ v, ω ] 2m[ v, ω ]
Первая составляющая 2m[ v, ω ] лежит в плоскости качаний и направлена
вдоль линии подвеса маятника. Поэтому данная сила всего лишь слегка меняет
натяжение нити, а с ней и период колебаний.
Вторая составляющая 2m[ v, ω ] хотя и ортогональна плоскости качаний,
но оказывает на нее слабое влияние. Во-первых, по причине своей малой
величины, во-вторых – вследствие периодического обращения своего
направления.
Под действием оставшихся сил уравнение относительного движения
принимает тот же вид, что и на полюсе, при замене ω ωв , в sin
Полный оборот плоскость качаний совершает за время
2
T
T
sin sin
T период вращения земли в инерциальной
системе отсчета
30
31.
На полюсах / 2 период обращения плоскости качаний равенпериоду обращения Земли вокруг своей оси, т.е. одним суткам.
Качание маятника в экваториальной плоскости 0 не сопровождается
поворотом плоскости качаний T , поскольку в этом случае
направление отвеса ортогонально вектору угловой скорости вращения
Земли: в sin 0.
Искривление траектории движения маятника под действием силы
Кориолиса в разных условиях возбуждения колебаний
1.
2.
В начальном состоянии маятник был максимально отклонен от
положения равновесия.
Маятнику сообщен толчок из положения равновесия.
а) траектория маятника
при запуске без толчка из
максимально удаленного
положения;
б) траектория маятника
при запуске толчком из
положения равновесия
31




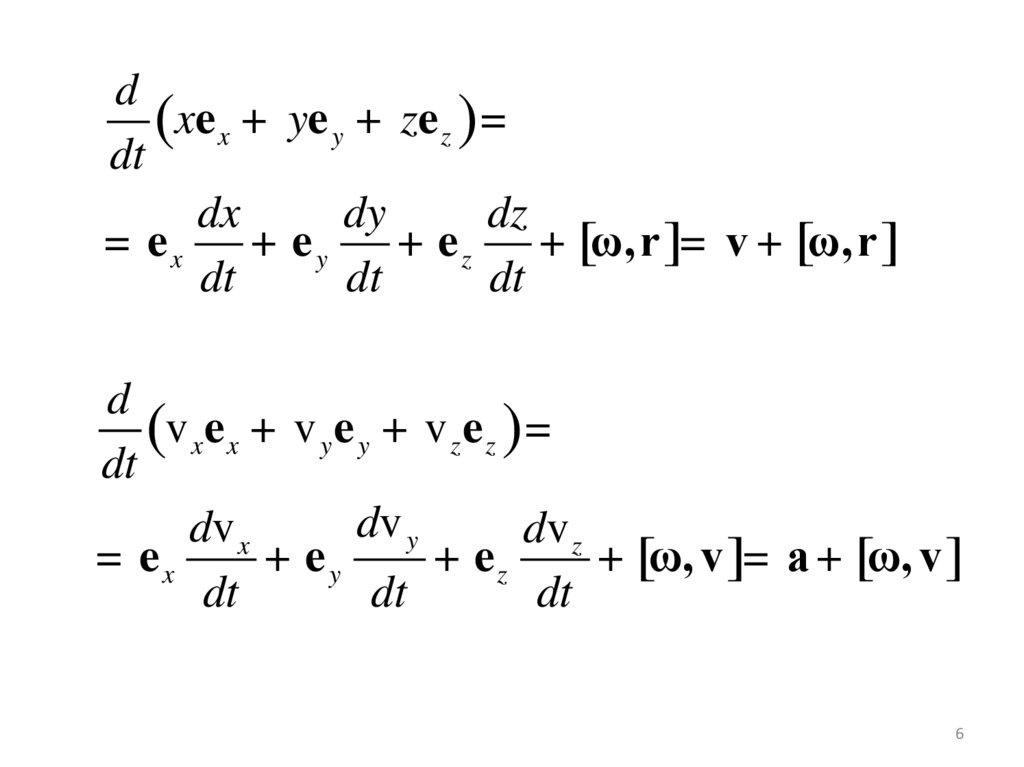
























 physics
physics








