Similar presentations:
Тригонометрическая форма записи комплексного числа
1.
2.
3.
4.
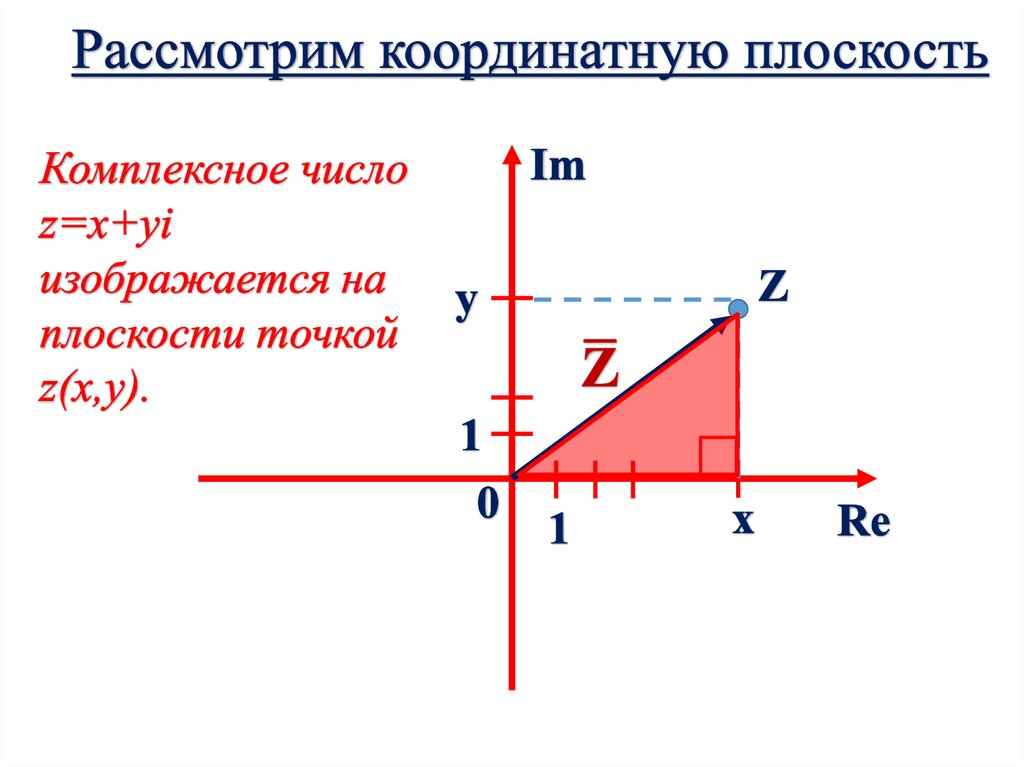
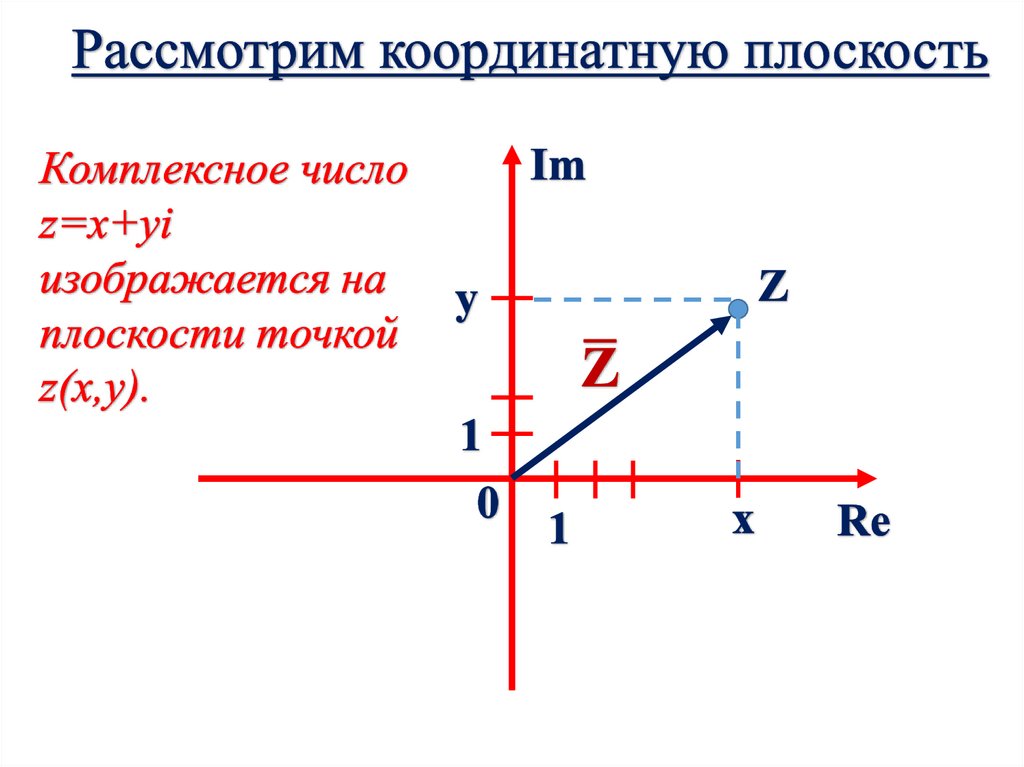
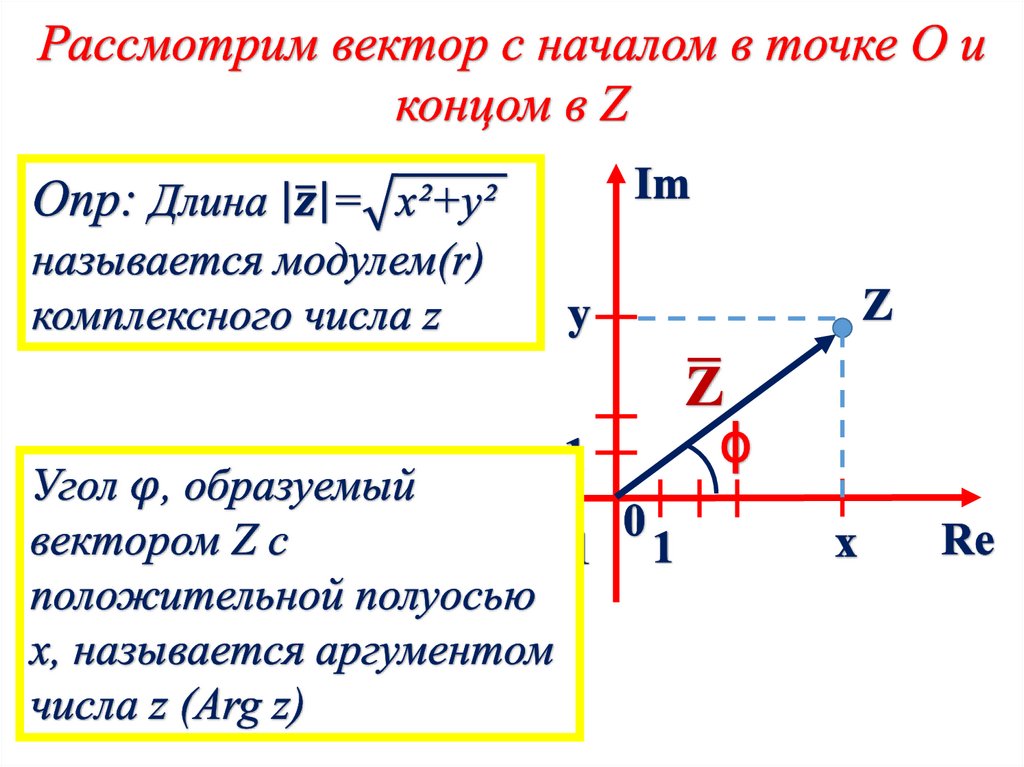
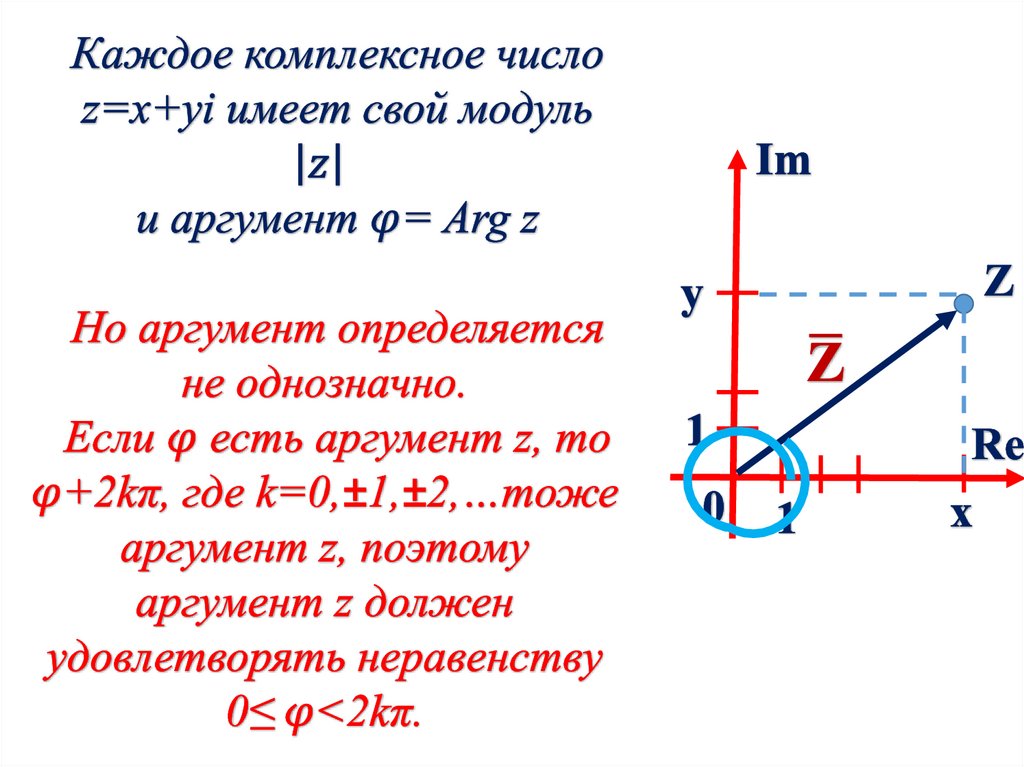
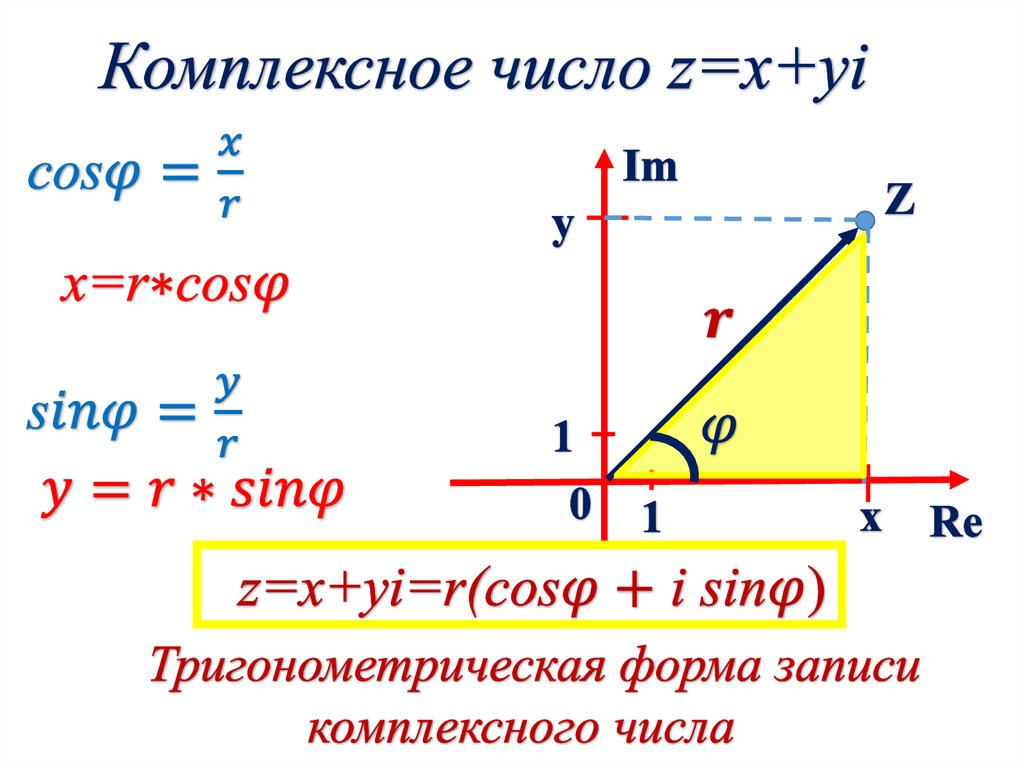
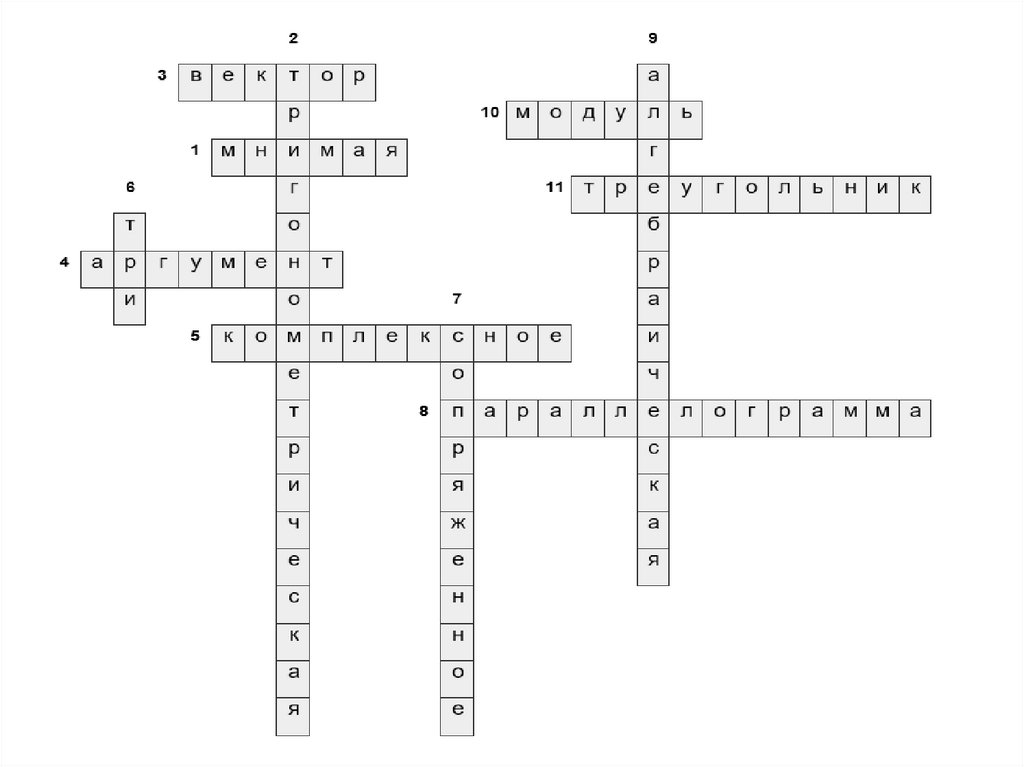
Тригонометрическаяформа записи
комплексного числа
5.
6.
7.
8.
9.
10.
11.
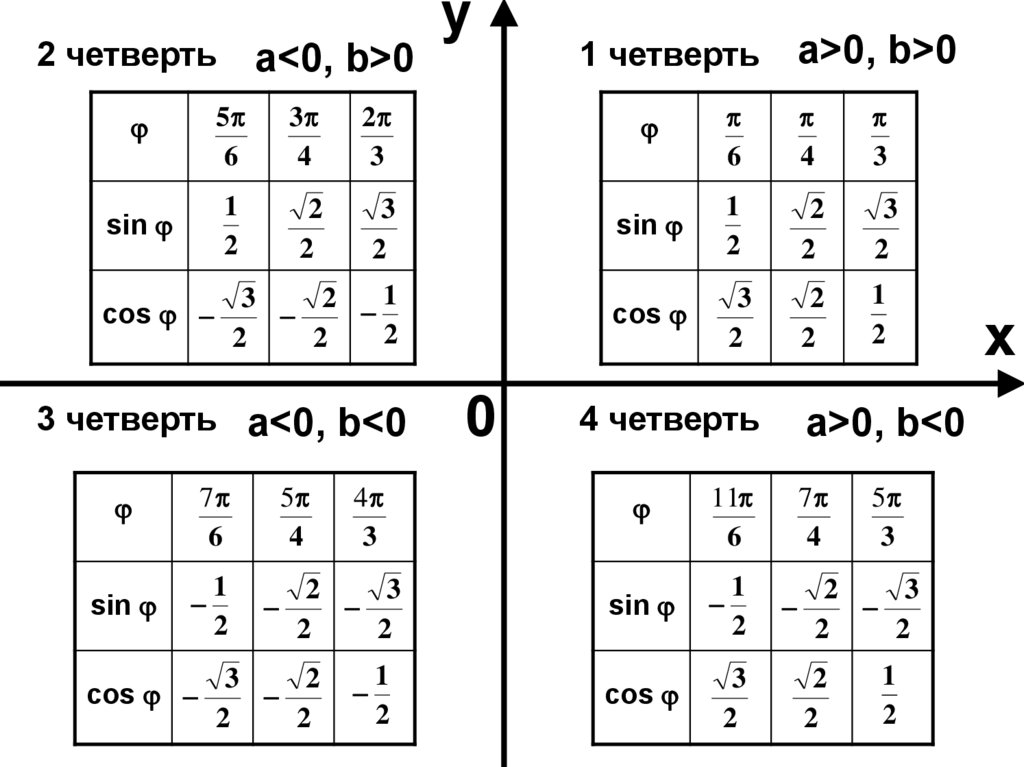
2 четвертьa<0, b>0
5
6
3
4
2
3
sin
1
2
2
2
3
2
y
1
3
2
cos
2
2
2
3 четверть a<0, b<0
7
6
sin
cos
1
2
5
4
4
3
2
3
2
2
3
2
2
2
1
2
0
a>0, b>0
1 четверть
6
4
3
sin
1
2
2
2
3
2
cos
3
2
2
2
1
2
4 четверть
sin
cos
a>0, b<0
11
6
1
2
3
2
7
4
5
3
2
3
2
2
2
2
1
2
x
12.
13.
14.
Правило №1. УмножениеПри умножении двух комплексных чисел,
заданных в тригонометрической форме, их
модули перемножаются, а аргументы
складываются.
z1 z 2 r1 r2 cos 1 2 i sin 1 2
15.
33
2
2
z 1 2 cos i sin и z 2 5 cos i sin .
8
8
3
3
3 2
3 2
z 1 z 2 2 5 cos i sin
8 3
8 3
3 2
3 2
10 cos i sin
3
3
8
8
16.
9 169 16
10 cos
i sin
24
24
7
7
10 cos i sin .
24
24
17.
Правило №2: ДелениеПри делении двух комплексных чисел,
заданных в тригонометрической
форме, их модули делятся, а аргументы
вычитаются.
z 1 r1
cos 1 2 i sin 1 2
z 2 r2
18.
55
7
7
z1 32 cos i sin и z 2 8 cos i sin .
9
9
12
12
z1 32 5 7
5 7
cos i sin
z 2 8 9 12
9 12
5 7
5 7
4 cos i sin
9 12
9 12
19.
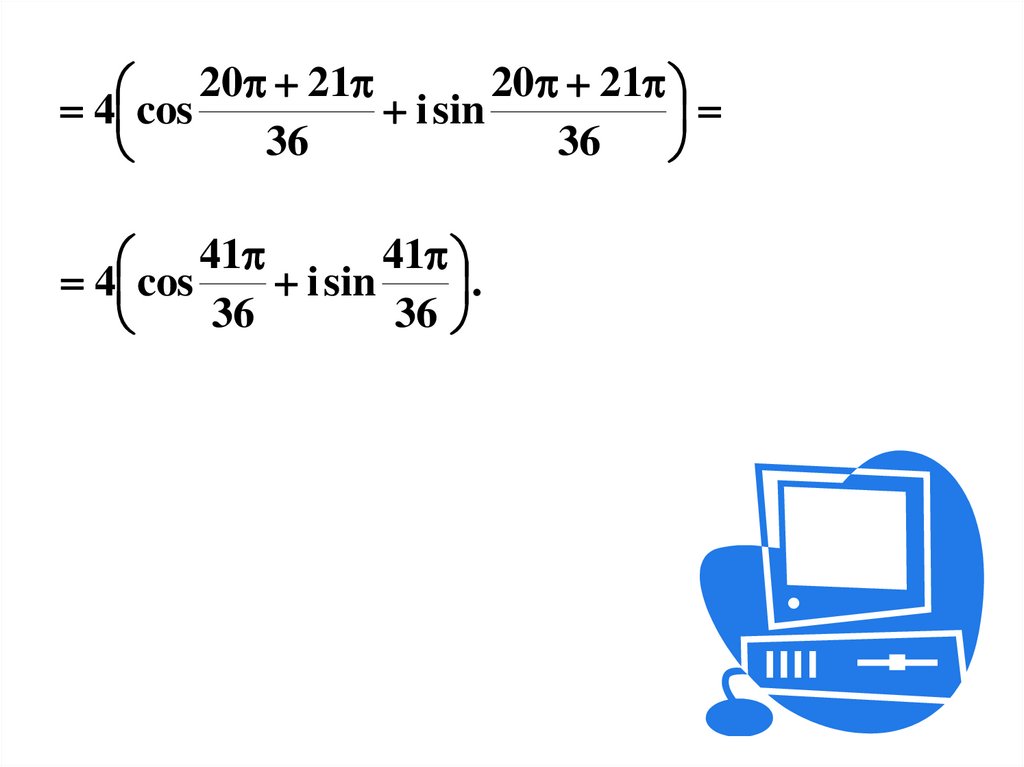
20 2120 21
4 cos
i sin
36
36
41
41
4 cos
i sin
.
36
36
20.
а) 3 (cos π/2 + i sin π/2)· (cos π/6 + i sin π/6);б) √3 (cos π/3 + i sin π/3)·√12 (cos π/6 + i sin π/6);
в) [18 (cos 47º + i sin 47º)]:[9 (cos 17º + i sin 17º)];
г) [20 (cos 72º + i sin 72º)]:[5 (cos 12º + isin 12º)]









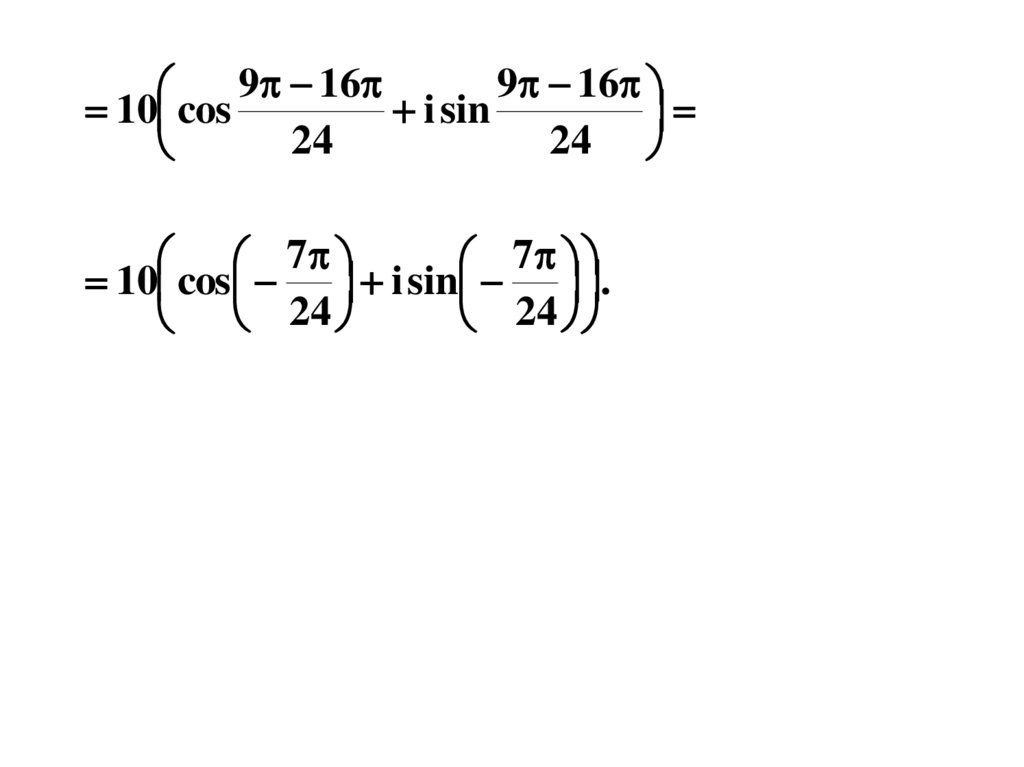







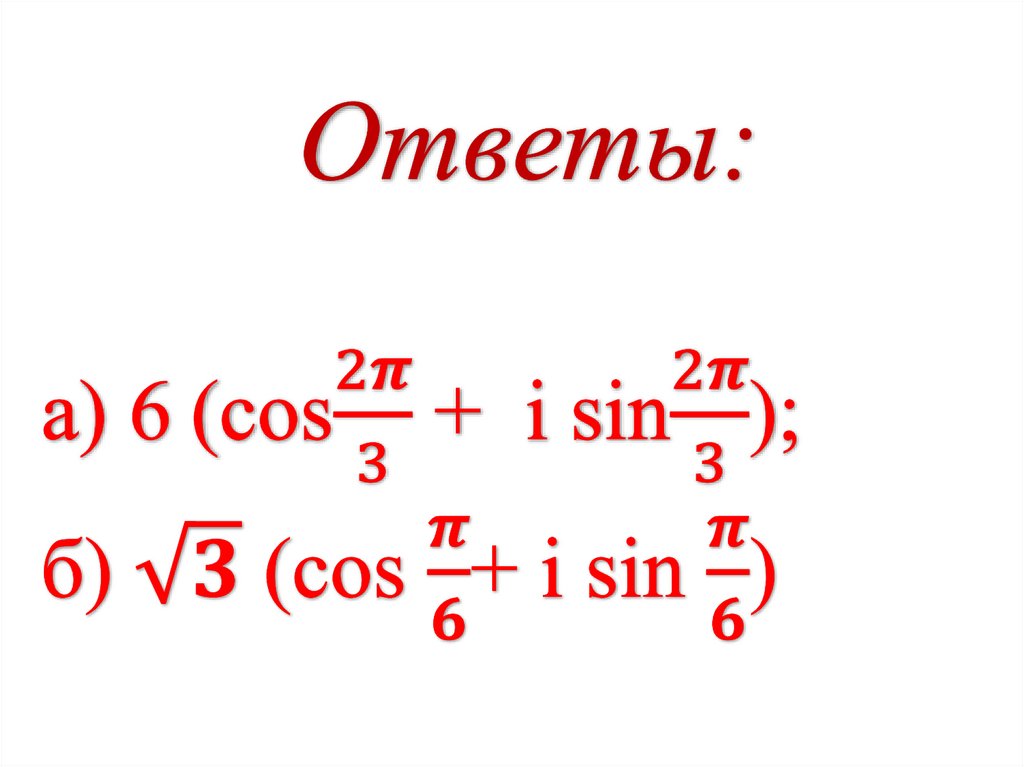









 mathematics
mathematics








