Similar presentations:
Комплексные числа
1.
Урок обощения по теме«Комплексные числа» в 10 классе»
2. Цель занятия: повторение и обобщение знаний по теме; с выходом на ознакомление с элементами теории функций комплексной
переменной.1
2
3
4
Задачи:
- повторение вопросов теории
- вычислительная работа, связанная с
алгебраической формой комплексного числа
- практическая работа, связанная с
геометрической интерпретацией
комплексных чисел, выход на функции
комплексных переменных
– итоговый контроль
3.
Лента времени1500 1600 1700 1800 1900 2000
t
4.
Лента времени1500 1600 1700 1800 1900 2000
1545 Италия
Д.Кардано
х у 10
ху 40
t
5.
Лента времени1500 1600 1700 1800 1900 2000
1572 Италия
Р. Бомбелли
t
(а + bi) + (c + di) = (а + с) + (b + d)i
(а + bi) - (c + di) = (а - с) + (b - d)i
(а + bi)·(с + di) = (ac - bd) + (ad + bc)i
a bi (a bi)(c di) ac bd bc ad
2
2
i
2
2
c di (c di)(c di) c d
c d
6. Выполните действия, ответы запишите в тетрадь
1) (3+2i)+3(-1+3i)2)
3) (1+i)(1-i)
4)
3
i
5)
i-2-(6-5i)
i3 ,
i101
(1 i) 4
6)
Разложите на множители в комплексных числах:
7) х 1,
2
8) а 4b ,
2
2
9) x 16
4
7. Проверь себя!
1) 11i2) -8+6i
3) 2
4) –i, i
5) -3i
6) -4
7)(x-i)(x+i)
8)(a+2bi)(a-2bi)
9) (x-2)(x+2)(x-2i)(x+2i)
8.
Лента времени1500 1600 1700 1800 1900 2000
1637,
Р.Декарт
t
9.
« Мнимые числа - этопрекрасное и чудесное
убежище божественного
духа, почти что амфибия
бытия с небытием»
(Г.Лейбниц)
10.
Лента времени1500 1600 1700 1800 1900 2000
1748 Л. Эйлер
t
11. Словарь терминов
Комплексный-лат. составной,сложный. Термин введён Гауссом
i-первая буква французского
слова imaginaire, мнимый
Инверсия, inversio - лат.
переворачивание
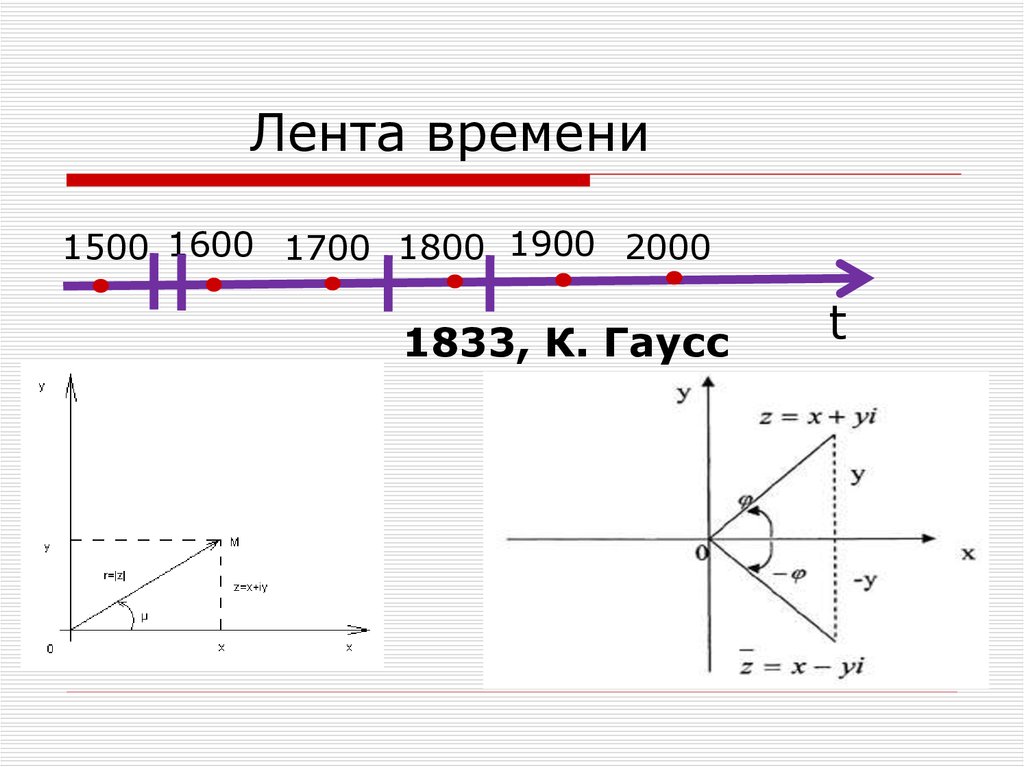
12.
Лента времени1500 1600 1700 1800 1900 2000
1833, К. Гаусс
t
13. Основные определения
Число вида z=a+bi называется комплексным, а иb-действительные числа, i-мнимая единица
Re z=a, Im z=b
Модулем комплексного числа называется
z a 2 b2
Аргументом комплексного числа z называется угол
между положительным направлением полуоси ОХ и
радиус-вектором ОМ, М(а,b)
Главный аргумент arg z заключен в границах
( ;
Тригонометрическая форма комплексного числа
z z cos i sin
14. Основные формулы
z a biz z a 2 b2
z1 z1 (cos 1 i sin 1 ), z 2 z 2 (cos 2 i sin 2 )
z1 z2 z1 z2 (cos( 1 2 ) i sin( 1 2 ))
z1 z1
cos( 1 2 ) i sin( 1 2 )
z2 z2
z n z (cos( n ) i sin( n ))
n
формула Му авра (1707)
15. Тригонометрическая форма комплексного числа
Изобразите комплексное число на плоскости z=-2+2iЗапишите данное число в тригонометрической форме
---------------------------------------------------------------------
16. Тригонометрическая форма комплексного числа
Изобразите комплексное число на плоскости z=-2+2iЗапишите данное число в тригонометрической форме
---------------------------------------------------------------------
3
z 2 2 , arg z
4
3
3
z 2 2 cos
i sin
4
4
17. Решите задачу различными способами в алгебраической и тригонометрической форме
Найдите z , если 3z z 4 8i6
18. Указания к решению
1 способ.Если z=x+iy, то получаем уравнение
3x+3yi-x+yi=-4+8i,
x+2yi=-2+4i,
Используем условие равенства комплексных чисел,
получаем, что х=-2, у=2.
При возведении в квадрат, получаем число -8i,
которое возводим в куб.
Ответ: 512i
2 способ.
Представленное в тригонометрической форме число
возвести по формуле Муавра в 6-ю степень.
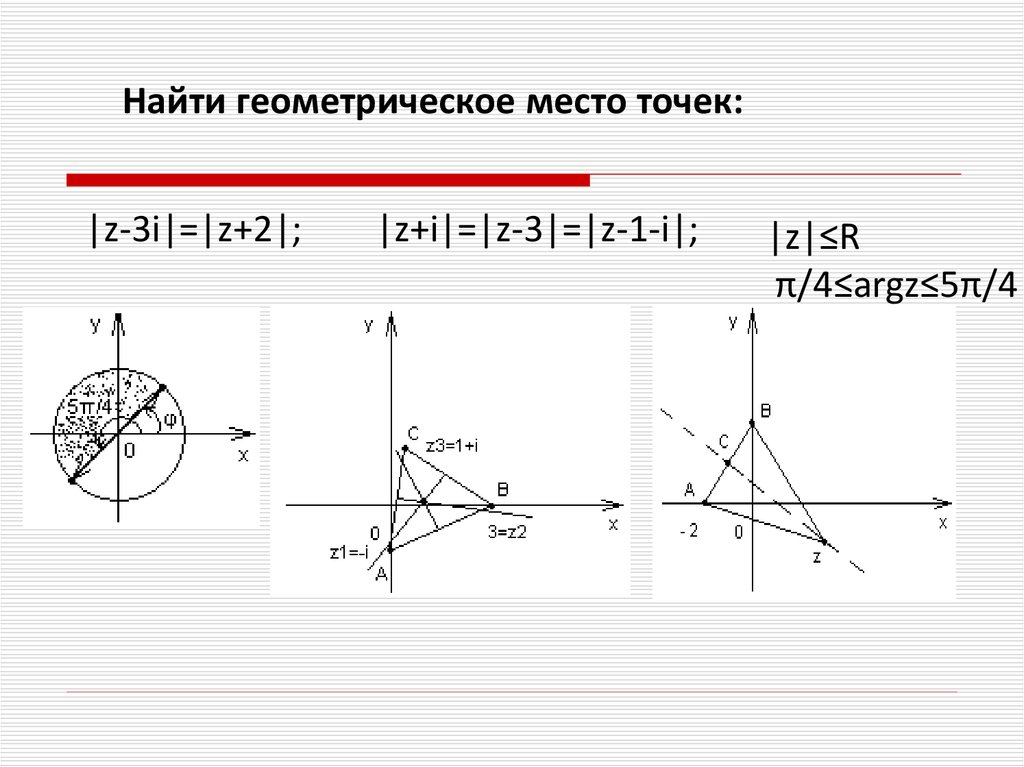
19. Геометрическое место точек
Изобразить на плоскости ГМТ, удовлетворяющих условиям:№1. z i 1,5
№ 2. Im z 2
№3.
arg z
6
4
№ 4. Re( z 2 ) 0
№5.Решения уравнения w 6 1 0
20. Полученные ГМТ
№1.№2.
№3.
№4.
№5.
Окружность с центром (0;-1) и радиусом 1,5
Полуплоскость у 2.
Угол, заключенный между заданными лучами.
Прямые у=х и у=-х.
Точки, расположенные в вершинах правильного
6-тиугольника с центром (0;0).
Модуль равен 1.
Простейший аргумент
6
21. Функции комплексного переменного
Задайте условиямичетверть круга с центром в
точке (0;0), радиусом 2.
Выполните
преобразования и
постройте ГМТ w,
удовлетворяющее
условию:
Выполните:
I вариант - а, в, д
II вариант - б, г, д.
а ) w z (3 i )
б )w 2 z
в ) w z (1 i )
г)w z3
д) w
1
z
22. Решения задач
0 arg z2
z 2
a ) параллельный перенос на вектор (3;1).
б ) гомотетия с центром (0;0) и коэффициен том 2.
z z (cos i sin ); w 2 z (cos i sin )
в ) поворот
на
угол
по часовой стрелке;
4
гомотетия с коэффициен том 2 и центром (0;0)
z z (cos i sin ); 1 - i 2 (cos i sin )
4
4
w 2 z (cos i sin )
4
4
23. Решения задач
г)w z (cos 3 i sin 3 );
д)
w 8
3
0 arg w
2
1 1(cos00 i sin 00 );
3
w
1
(cos( 00 ) i sin( 00 );
z
w
1
(cos( ) i sin( ).
z
1
w
2
arg w 0
2
Внутренние точки переходят во внешние,
штриховка вне фигуры.
Такое
преобразов ание называется
инверсией .
24. Этап 4. Итоговый тест. Проверь себя! ( «да» или «нет»)
1.Число 1+i
является действительным?
2.
-2(cos90 0+i sin90 0) - является тригонометрической
формой комплексного числа?
3.
Многочлен (х+4) можно разложить на множители в
комплексных числах?
4.
Если комплексное число равно своему сопряженному, то
оно является действительным?
5.
1
3
i
2
2
имеет аргумент равный /3 ?
Число
25. Ответы
1.2.
3.
4.
5.
Нет
Нет
Да
Да
Нет
*
26.
Лента времени1500 1600 1700 1800 1900 2000
1843
У.Р. Гамильтон
t
q = x + yi + uj + vk,
где i, j, k – новые числа, являющиеся аналогом
мнимой единицы в комплексных числах.
27.
Домашнее задание:34.38, 35.42, 32.36(а, б)
28.
«Мысль выражать все числа знакаминастолько проста, что именно из-за этой
простоты сложно осознать, сколь она
удивительна»
Пьер Симон Лалас
29.
Вам поклоняюсь, вас желаю, числа!Свободные, бесплотные как тени,
Вы радугой связующей повисли
К раздумиям с вершины вдохновенья.
Валерий Яковлевич Брюсов
(русский писатель, 1873-1924)
30.
Дополнительные задачиКаков геометрический смысл
выражений:
а) |z|,
б)Argz;
в) |z1-z2|,
г) Arg(z1/z2)?
31.
Найти геометрическое место точек:|z-3i|=|z+2|;
|z+i|=|z-3|=|z-1-i|;
|z|≤R
π/4≤argz≤5π/4
32.
Вычислить:2
3
10
ii i …i =?
33.
Доказать, что3
2
cos3φ=cos φ-3sin φcosφ;
sin3φ=3cos2φsinφ-sin3φ.
34.
Найти действительныерешения уравнения
(3+i)x+(-5+2i)y=4+16i.
35.
Найти все значения корня 4√1+i√3.Дать геометрическую иллюстрацию.
36.
37.
Представить валгебраической форме
комплексное число
1/(1+i√3)6-1/(√3-i)6 =z
38.
Решить уравнениеz2 – (4+3i) z +1 + 5i = 0


































 mathematics
mathematics








