Similar presentations:
Тригонометрическая форма комплексного числа
1. Тригонометрическая форма комплексного числа
2. Историческая справка
Геометрическоепредставление
комплексных
чисел
называют
иногда
«диаграммой Аргана» в
честь
швейцарского
ученого Жана Роберта
Аргана.
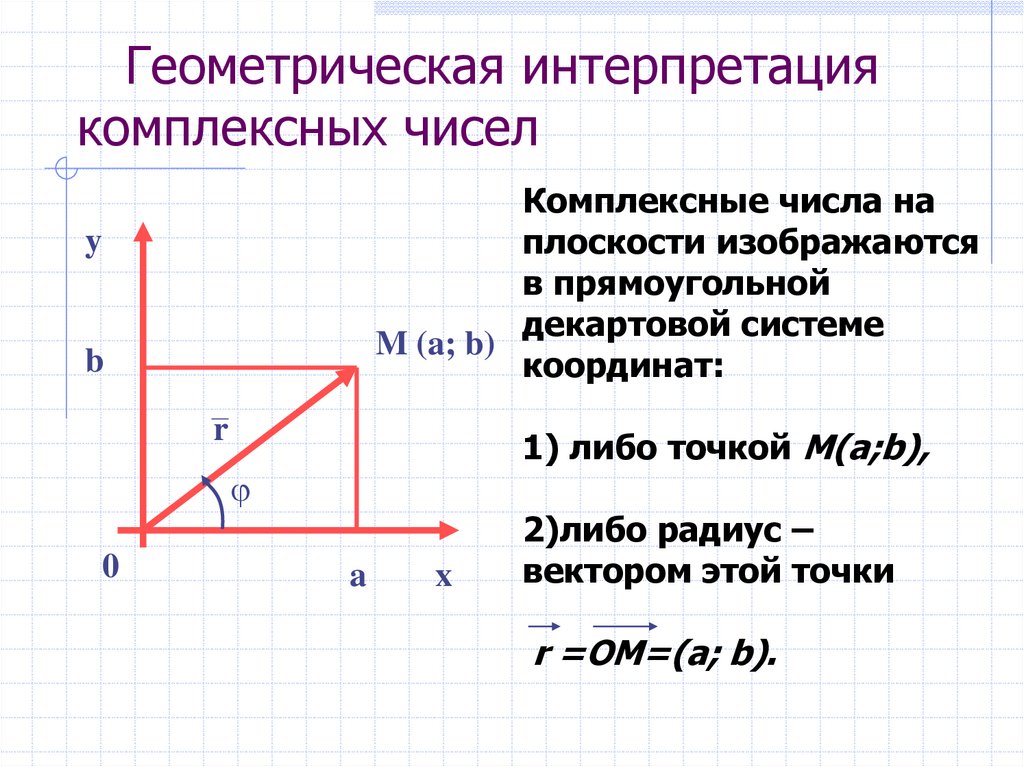
3. Геометрическая интерпретация комплексных чисел
Комплексные числа наплоскости изображаются
в прямоугольной
декартовой системе
M (a; b)
координат:
y
b
r
1) либо точкой М(а;b),
0
a
x
2)либо радиус –
вектором этой точки
r =ОМ=(а; b).
4. Модуль и аргумент комплексного числа
Аргументкомплексного числа
Модуль комплексного
числа
z = r = a b
2
cos =
a
a b
2
2
2
= arg z=arg(a+bi),
-π < .
и sin =
b
a b
2
2
5. Тригонометрическая форма к. ч.
yM (a; b)
b
r
0
a
x = r cos
y = r sin
x
z = a bi = r(cos isin )
6. Самостоятельная работа «Умножение и деление комплексных чисел, заданных в тригонометрической форме »
1. Изучить теоретический материал и выписатьформулы умножения и деления к.ч. в
тригонометрической форме(п.3 стр.235)
2. Разобрать задачи № 29-32 стр.236-237
3. Решить в тетради задачи(стр.238-239):
№ 38(2,4,6)
№ 39(2,4,6)
№ 40(1,3)
Учебник в СЭО
Н.В. Богомолов Практические занятия по математике
7. Умножение и деление комплексных чисел, заданных в тригонометрической форме
Теорема 1.z1 = r1 cos 1 i sin 1 ,
z2 = r2 cos 2 i sin 2 ,
z1 0, z2 0
1) z1z2 = r1r2 cos 1 2 i sin 1 2
z1 r1
2)
= cos 1 2 i sin 1 2
z 2 r2






 mathematics
mathematics








