Дифференцируемость функции в точке

1.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ В ТОЧКЕ
f x0 x f x0
y
f x0 lim
lim
x 0 x
x 0
x
df
f x0 x f x0
,
x 0
x
f x0 lim
f x0 x f x0 0
f x0 0 lim
,
x 0
x
f x0 x f x0
,
x 0
x
f x0 lim
f x0 x f x0 0
f x0 0 lim
x 0
x
Теорема. Для существования производной функции в т. x0 необходимо и
достаточно существования в т. x0 правой и левой производных и их равенства.
Замечания:
1 . Определение производных имеет локальный характер
2 . Если функция f в точке x0 непрерывна справа (слева), то
f x0 0 f x0 , (соответственно, f x0 0 f x0 ).
1

2.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ В ТОЧКЕ
Функция y f x называется дифференцируемой в точке x0 , если
y A x x x при x 0
(5.2)
где x – бесконечно малая функция.
!!! Функция x может принимать в т. x 0 какое угодно значение. Для
определенности будем считать, что 0 0 , т.е. x непрерывна в т. x 0 .
!!! x x o x
y A x o x , при x 0 .
(0.1)
Линейная однородная функция A x (от переменной x ) называется
дифференциалом функции f в точке x0 и обозначается df x0 или dy .
!!! Дифференциал dy A x определен для любого значения x :
x , а приращение y f x0 x f x0 , можно рассматривать
только для таких x , для которых x0 x принадлежит области определения
функции f .
!!! Приращение x обозначают dx и называют дифференциалом независимой
2
переменной (или простейшим дифференциалом).

3.

!!! Дифференциал dx независимой переменной равен приращению x этой
переменной. Дифференциал dy A dx зависимой переменной y y x , в общем
случае, не равен приращению y :
d sin x cos x dx cos x x
d sin x x
4
2
x
2
d sin x x 0
2
d sin x x 0 x
!!! Понятие дифференциала определено только для дифференцируемых
функций. Причем дифференциал в точке определяется однозначно.
3

4.

3 . Если dy 0 , то главная часть приращения функции y в точке x0 является
линейной функцией относительно x , при этом приращение y и дифференциал
dy – эквивалентные бесконечно малые при x 0 функции.
Если dy 0 , то приращение y при x 0 является бесконечно малой
более высокого порядка, чем x .
4 . Выражение y A x x x можно записать в виде
f x f x0 A x x0 o x x0 , x x0 .
Если функция f x дифференцируема в точке x0 , то в окрестности точки x0 она
ведет себя «почти как линейная функция» f x0 A x x0 , причем погрешность
при замене функции f этой линейной функцией тем меньше, чем меньше разность
x x0 , и, более того, отношение этой погрешности к разности x x0 стремится к
нулю при x x0 .
4

5.

Необходимое и достаточное условие дифференцируемости функции в точке.
« f x дифференцируема в т. x0 »
« f x имеет в т. x0 конечную производную».
З а м е ч а н и е . Теорема позволяет отождествлять понятия дифференцируемости функции в данной точке с понятием существования у функции в данной
точке конечной производной. Поэтому операцию нахождения производной
принято называть дифференцированием.
5

6.

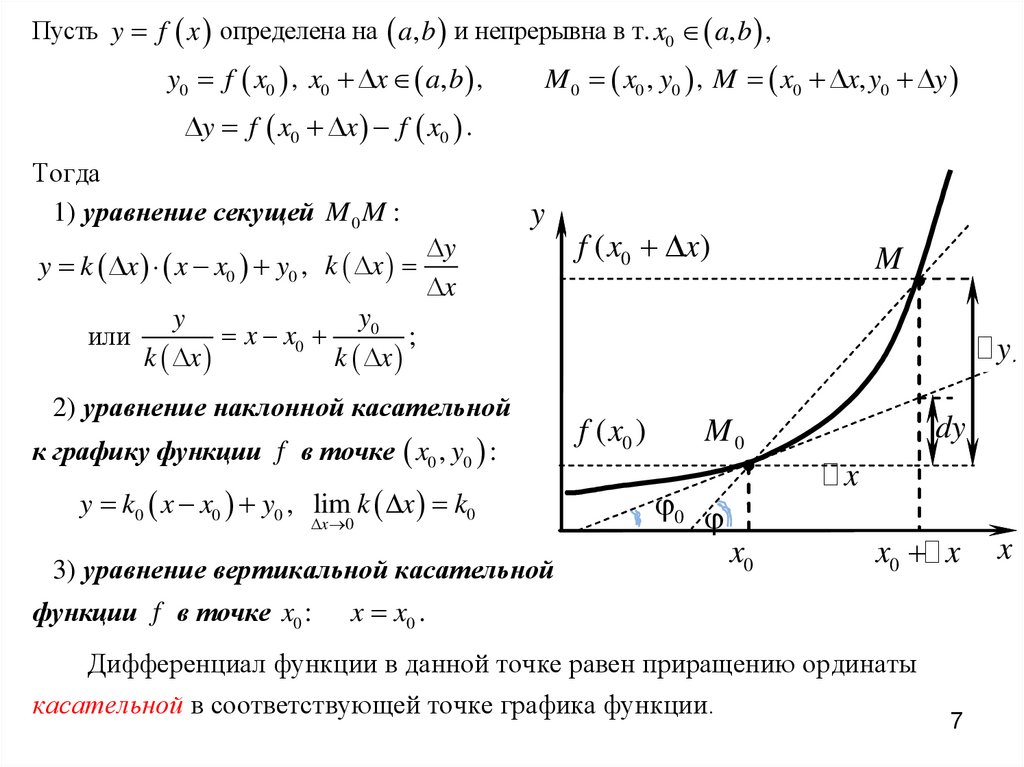
Пусть y f x определена на a, b и непрерывна в т. x0 a, b ,
y0 f x0 , x0 x a, b ,
M 0 x0 , y0 , M x0 x, y0 y
y f x0 x f x0 .
Тогда
1) уравнение секущей M 0 M :
y k x x x0 y0 , k x
или
y
x
y
f ( x0 x)
M
y0
y
x x0
;
k x
k x
2) уравнение наклонной касательной
к графику функции f в точке x0 , y0 :
y k0 x x0 y0 , lim k x k0
x 0
3) уравнение вертикальной касательной
функции f в точке x0 :
y
f ( x0 )
dy
M0
x
0
x0
x0 x
x x0 .
Дифференциал функции в данной точке равен приращению ординаты
касательной в соответствующей точке графика функции.
7
x

7.

Геометрический смысл конечной производной и дифференциала
Теорема 5.3. Если функция y f x имеет в т. x0 конечную производную
f x0 , то график функции имеет в т. M x0 , f x0 наклонную касательную,
причем f x0 tg 0 , где 0 – угол между этой касательной и осью абсцисс.
Теорема 5.4. Пусть через точку x0 , y0 графика функции f x проходят
горизонтальная или наклонная прямая y x A x x0 y0 . Тогда
«прямая y x – касательная к графику функции f x в точке x0 , y0 »
« f x y x o x x0 при x x0 ».
(*)
Следствие. Если существует касательная к графику функции f x в точке x0 , y0 , то она единственна.
8

8.

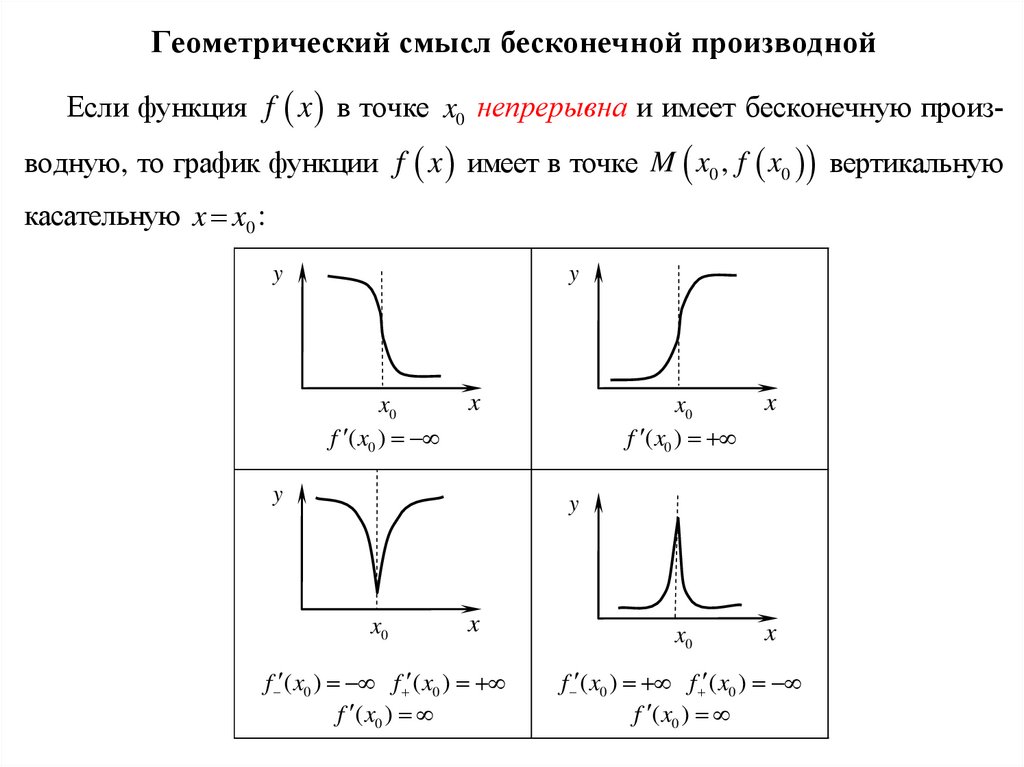
Геометрический смысл бесконечной производной
Если функция f x в точке x0 непрерывна и имеет бесконечную производную, то график функции f x имеет в точке M x0 , f x0 вертикальную
касательную x x0 :
y
y
x0
f ( x0 )
x
y
x0
f ( x0 )
x
x0
x
y
x0
x
f ( x0 ) f ( x0 )
f ( x0 )
f ( x0 ) f ( x0 )
f ( x0 )

9.

Геометрический смысл односторонних производных
Геометрический смысл правой (левой) производных –
предельное положение правой (левой) части секущей M 0 M относительно
точки M x0 , f x0 .
Замечания:
1 . Правая и левая касательные в точке x0 , также как и правая и левая
производные, определены только для функций, определенных в точке x0 .
2 . Существование и конечность левой (правой) производной эквивалентно существованию левой (правой) наклонной касательной.
3 . Из существования вертикальной левой (правой) касательной следует
бесконечность левой (правой) производной. Обратное утверждение,
вообще говоря, не верно.
Геометрический смысл обобщенных правой (левой) производных –
предельное положение правой (левой) касательных.
12

10.

Прямая, проходящая через точку M x0 , f x0 перпендикулярно касательной, называется нормалью. Если f x0 0 , то уравнение нормали записывается в виде
y y0 y f x0
1
x x0 .
f x0
Если f x0 0 , то нормаль имеет уравнение x x0 .
Пусть графики функций f1 x и f 2 x пересекаются в точке M . За угол
между графиками этих функций принимается величина угла, образованного
касательными, проведенными к графикам в точке M .
Если 1 f1 f 2 0 , то ; в остальных случаях
2
arctg
f1 f 2
.
1 f1 f 2
13

11.

Дифференцирование обратной функции
Теорема. Пусть функция y f x в некоторой окрестности точки x0
дифференцируема и имеет обратную, причем f x0 0 . Тогда обратная
функция x f 1 y имеет в точке y0 , x0 производную, равную
1
.
f x0
Замечание (геометрический смысл теоремы)
Рассмотрим в окрестности точки x0 график
функции y f x (или обратной функции). Пусть
точке x0 на графике соответствует точка M . Тогда
y
f ( x0 )
f x0 tg , f 1 y0 tg ,
где и – углы наклона касательной, проходящей
через точку M , к оси Ox и Oy соответственно. Так
M0
x0
x
как эти углы в сумме составляют 90 , то tg 1/ tg .
14

12.

Дифференцирование сложной функции
Теорема. Пусть x t – дифференцируема в т. t0 , y f x –
дифференцируема в т. x0 t0 . Тогда сложная функция f t
дифференцируема в т. t0 , причем f t0 f x0 t0 .
17

13.

ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
Функция f x сама по себе может иметь производную, ее называют производной второго порядка и обозначают f x или f
2
x .
Понятие производной n -го порядка вводится индуктивно: если f
n 1
x – дифференци-
руемая функция, то
f
n
x f
n 1
x
dn f
n
n f xn x , n , n 1 .
dx
Для обозначения производных до третьего порядка включительно обычно предпочитают
использовать штрихи: y , y , y или f x , f x , f x . Если порядок производной n 4 , то
для его обозначения допускается использование римских цифр, например,
y IV y или f IV x f 4 x .
4
!!! Перед тем как вычислять f f
n
n 1
обязательно упростите выражение для f .
n 1
Под производной нулевого порядка от функции f x понимается сама функция, т.е.
f x f x .
0
Формула Лейбница
uv u n v Cn1u n 1 v Cn2u n 2 v 2
n
uv ,
n
n раз
Функцию, имеющую на множестве X конечную производную n -го порядка, называют19
дифференцируемой на данном множестве.

14.

Вычисление производных параметрически заданной функции
Пусть функция y x задана уравнениями
y y t ,
x x t .
Тогда для вычисления ее производных высших
порядков используется цепочка формул
yt
yx ,
xt
y xx y x 'x
y x t'
xt
, (*)
Пример. Пусть,
y t4,
x ln t.
Тогда
4t 3
y x
4t 4 ,
1/ t
4t 4 '
t
y xx y x 'x
16t 4 ,
1/ t
16t 4 '
t
'
y
64t 4 .
xxx y xx x
1/ t
y xx t'
'
y xxx y xx x
,…
xt
Замечание. Во многих источниках для вычисления второй производной предлагают
использовать формулу
y x t'
'
y xx y x x
. (**)
xt
У этой формулы есть серьезные недостатки:
1) вычисления по формуле (**) обычно арифметически сложнее, чем по формуле (*),
2) такой формулы для третьей, четвертой и т.д. производной нет, а значит, для вычисления
производных 3,4, … порядков необходимо знать описанную технологию.
21

15.

Вычисление производных параметрически заданной функции
Для нахождения производной n -го порядка неявно заданной функции требуется
последовательное вычисление всех ее производных более низкого порядка.
Пример. Пусть функция y x задана неявно уравнение
x 4 y 4 xy 3 . (1)
1. Вычислим y , для этого продифференцируем (2):
4 x3 4 y 3 y y xy 0 . (3)
4 x3 y
Следовательно, y 3
.
4y x
2. Вычислим y Дважды дифференцируя (1) получим систему двух уравнений:
4 x 3 4 y 3 y y xy 0,
(4)
2
2
2
12 x 12 y y y y xy 0
Если из первого уравнения выразить производную y и подставить полученный
результат во второе уравнение, то останется лишь разрешить преобразованное второе
уравнение относительно y .
Замечание. Если требуется вычислить y в точке x0 , то надо сначала подставить
значение x0 в (3), а потом выразить y . Аналогично для производных старших порядков,
надо сначала получить систему (4) ((!!! Не переходя к дробям), потом подставить значение точки x0 , а уже после разрешать систему относительно требуемой производной.
22

16.

ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
Аналогично производной n -го порядка определяется дифференциала n -го порядка:
d n f x d d n 1 f x , n , n 1.
Замечание:
df
d f d df – «д квадрат f » – второй дифференциал f ,
2
df
df df – «д f в квадрате»,
2
d f
2
2
2 f df – «д от функции f » – первый дифференциал функции f .
df
2
2
Аналогично для дифференциалов n -го порядка:
d f d d n 1 f – n -ый дифференциал f ,
df
n
df
df df – «д f в n -й степени»,
n
d f
n
n
nf
df
n 1
df – «д от функции f n » – первый дифференциал функции f n .
Для независимой переменной x принято, что
df
df
dx x , n 1 d x 0.
n
23

17.

ИНВАРИАНТНОСТЬ ФОРМЫ ПЕРВОГО ДИФФЕРЕНЦИАЛА
Теорема 5.9. Пусть y f x – дифференцируема в точке x0 .
Независимо от того, является ли аргумент x независимой переменной
или дифференцируемой функцией некоторой новой переменной t ,
справедлива формула
dy f x0 dx .
(5.17)
Или, другими словами: производная функции y f x всегда равна
отношению дифференциала этой функции dy к дифференциалу аргумента dx , т.е. f x0
dy
.
dx
З а м е ч а н и е . Для дифференциалов более высоких порядков свойство не выполняется.
24