Производная, её геометрический и механический смысл. Уравнения касательной и нормали к кривой. Дифференцируемость функции

1. Лекция 8. Производная, её геометрический и механический смысл. Уравнения касательной и нормали к кривой. Дифференцируемость

функции
в точке.
Правила дифференцирования.

2.

ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ
Задача о вычислении скорости
Пусть материальная точка совершает прямолинейное (вообще говоря,
неравномерное) движение по закону s f t , где t – время, s – путь за это
время. Иными словами, расстояние пройденное точкой от некоторого
начального положения за какое-то время описывается как функция времени,
за которое пройдено это расстояние. Зафиксируем момент времени t0 и t, за
t t t0 ,
промежуток
времени
эта
пройдет
расстояние
S f t f t0 f t0 t f t0
S
vcp
- средняя скорость движения точки на участке S за время t
t
Будем уменьшать промежуток t , при этом средняя скорость будет
меняться.
f t f t0
S
Df. Величина lim
* называется мгновенной
lim
t 0 t
t 0
t t0
скоростью движения точки в момент времени t0.

3.

Задача о проведении касательной.
Общее определение касательной:
M0 l
M l
M 0M
Df. Пусть задана некоторая кривая l на плоскости и точка М0 на этой
кривой. Рассмотрим другую точку этой кривой М. Рассмотрим секущую этой
кривой М0М. Будем устремлять М к точке М0 по кривой. При этом секущая
будет изменять свое положение. Если секущая М0М при стремлении точки М
по кривой к точке М0 по кривой стремится занять некоторое предельное
положение М0Т (независимо от того, с какой стороны кривой точка М
приближается к М0), то эта прямая М0Т называется касательной к кривой l в
точке М0. (Иными словами, касательная – предельное положение секущей)

4.

Формулировка задачи о проведении касательной:
Пусть задана функция y = f(x) (говорят, что задана кривая y = f(x)).
Известно, что в точке х0 существует касательная к графику функции y =
f(x). Найти угловой коэффициент к этой касательной: tg ?
Проводим секущую М0М с углом φ
y f x f x0
M 0 MA :
x x x 0
M 0 x0 ; y0
M x; y
tg ?
y f x f x0
x
x x0
f x f x0
y
* *
tg lim tg lim
lim
x 0 x
x x0
x x0
Решая разные, казалось бы, по своему характеру задачи, мы пришли к
(*) и (**) совершенно одинаковой природы.
Из M 0 MA : tg

5.

Понятие производной
Df 1. Пусть функция y = f(x) определена на a; b , x a; b . Если
f x f x0
y
lim
существует конечный предел lim
, то он называется
x x0
x 0 x
x x0
производной данной функции в данной точке.
df x0
dy
Обозначается: f ' x0 y' x0 y' x x0
dx x x0
dx
dy
«дэ игрек по дэ икс»
dx
Замечание:
f x f x0
Рассмотрим f x0 lim
. Он представляет собой предел
x x0
x x0
f x f x0
0
Ф x
: x0 D Ф . Он представляет собой неопределенность
x x0
0

6.

Df 2. Если каждой точке x a; b поставить в соответствие
производную функции f’ в этой точке, то мы получим функцию, которая
называется производной данной функции f ' x . Производная функции в
точке – это число.
Df 3. Если функция имеет производную в точке х0, то она называется
дифференцируемой в этой точке. Функция называется дифференцируемой на
множестве, если она дифференцируема в каждой точке множества.
Процесс нахождения производной называется дифференцированием.
Возвращаясь к задаче о вычислении скорости, механический смысл
производной: производная пути по времени: s' t0 есть мгновенная скорость
движения.
Возвращаясь к задаче о проведении касательной, получим
геометрический смысл производной: f ' x0 - угловой коэффициент
касательной графику функции y = f(x) в соответствующей точке графика
x0 , f x0

7.

Пример.
Задача:
Найти производную функции y x 2
а) в произвольной точке х
б) при х = 4
Решение:
а) х - приращение аргумента в этой точке;
у - приращение функции в этой точке
y f x x f x x x x 2 x 2 2 x x x 2 x 2 x 2 x x
2
y
x 2 x x
lim
2x
x 0 x
x 0
x
2
(х )’=2x
б) (х2)’ х 4 =2·4=8
y' lim

8.

§3. Уравнения касательной и нормали
M 0 l ,перпендикулярной
Прямая,
проходящая
через
точку
касательной к кривой l в этой называется нормалью к заданной кривой в
данной точке. Пусть y = f(x) – кривая и в точке М0(x0;f (x0)) существует
касательная.

9.

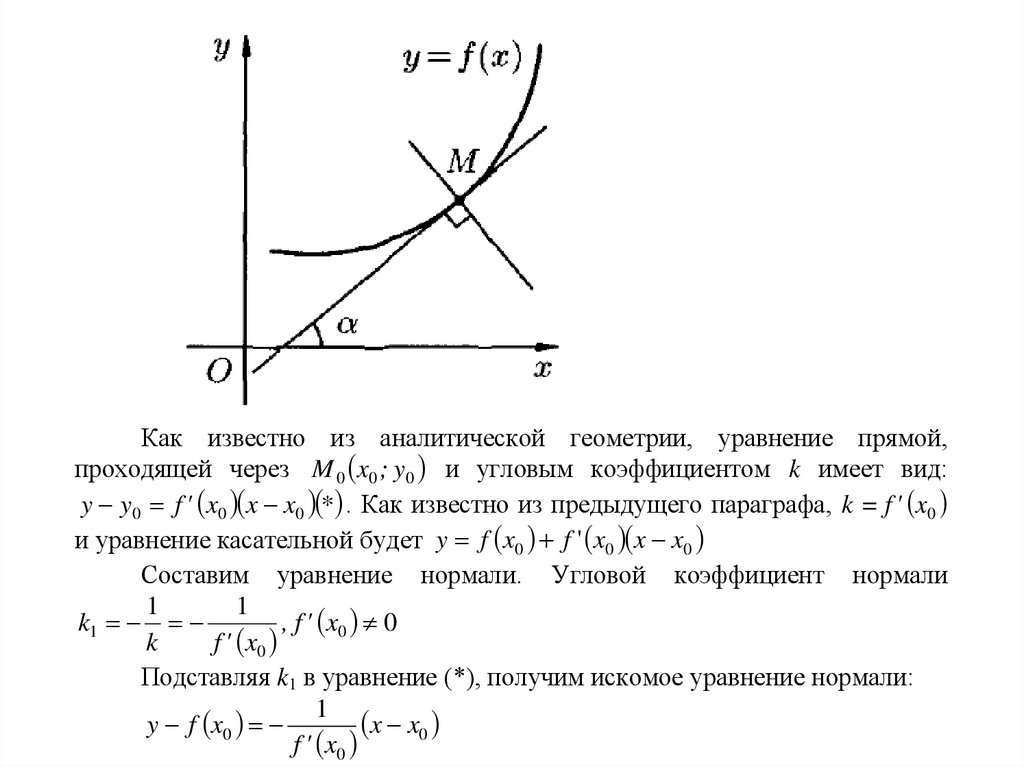
Как известно из аналитической геометрии, уравнение прямой,
проходящей через M 0 x0 ; y0 и угловым коэффициентом k имеет вид:
y y0 f ' x0 x x0 * . Как известно из предыдущего параграфа, k = f ' x0
и уравнение касательной будет y f x0 f ' x0 x x0
Составим уравнение нормали. Угловой коэффициент нормали
1
1
k1
, f ' x0 0
k
f ' x0
Подставляя k1 в уравнение (*), получим искомое уравнение нормали:
1
x x0
y f x0
f ' x0

10.

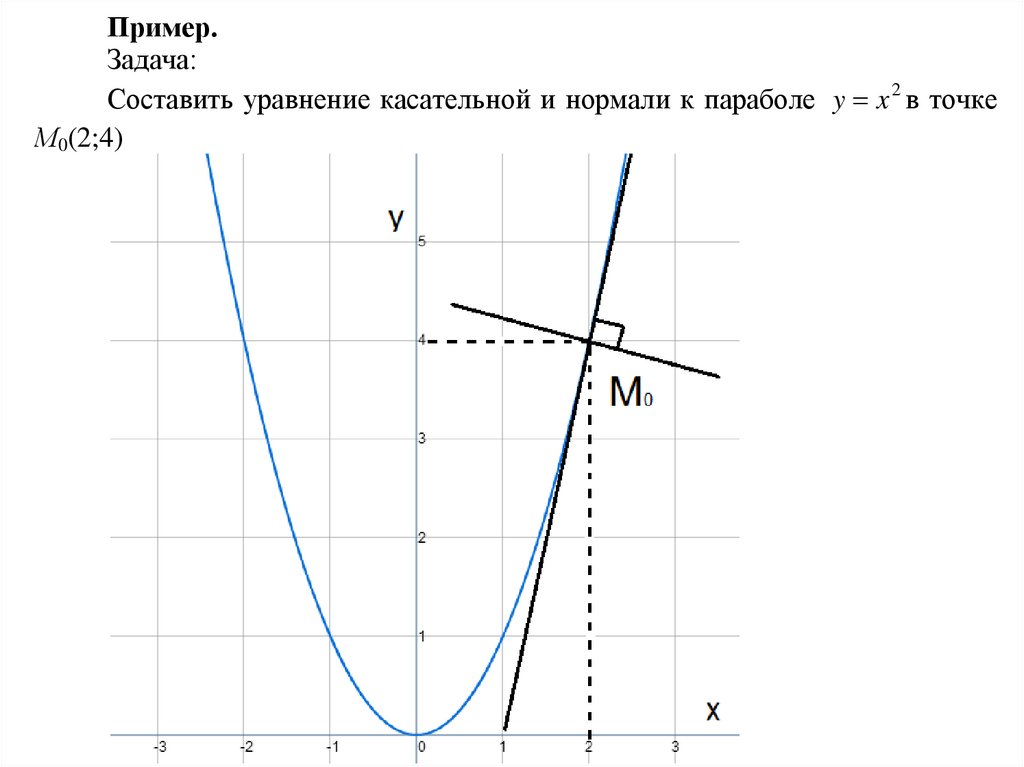
Пример.
Задача:
Составить уравнение касательной и нормали к параболе y x 2 в точке
М0(2;4)

11.

y'
x 2
4 k
y 4 4 x 2
y 4x 4
4 x y 4 0 - уравнение касательной
1
k1
4
1
y 4 x 2
4
4 y 16 x 2
x 4 y 18 0 - уравнение нормали.

12.

Непрерывность функции, имеющей производную.
Th (о непрерывности дифференцируемой функции):
Если функция y = f(x) дифференцируема в точке х0, то она непрерывна в
этой точке.
Доказательство:
y Th*
Пусть функция дифференцируема в точке х0, т.е. f ' x0 lim
эта
x 0 x
функция представима в виде суммы:
y
f ' x0 x ; где x 0
x
x 0
y x f ' x0 x
x 0 y 0 т.е. бесконечно малому приращению аргумента
соответствует бесконечно малое приращение функции и, стало быть, эта
функция непрерывна.
Ч.т.д.

13.

Замечание 1:
Обратное утверждение, вообще говоря, а именно из того, что функция
непрерывна в точке не следует, что она дифференцируема в этой точке.
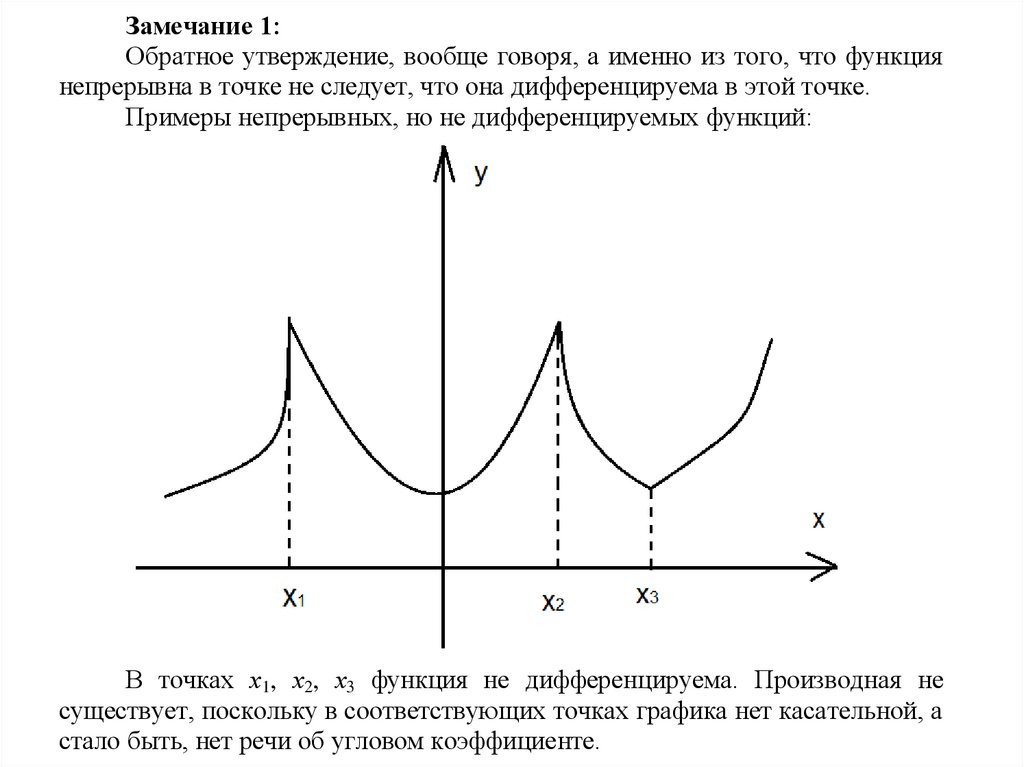
Примеры непрерывных, но не дифференцируемых функций:
В точках х1, х2, х3 функция не дифференцируема. Производная не
существует, поскольку в соответствующих точках графика нет касательной, а
стало быть, нет речи об угловом коэффициенте.

14.

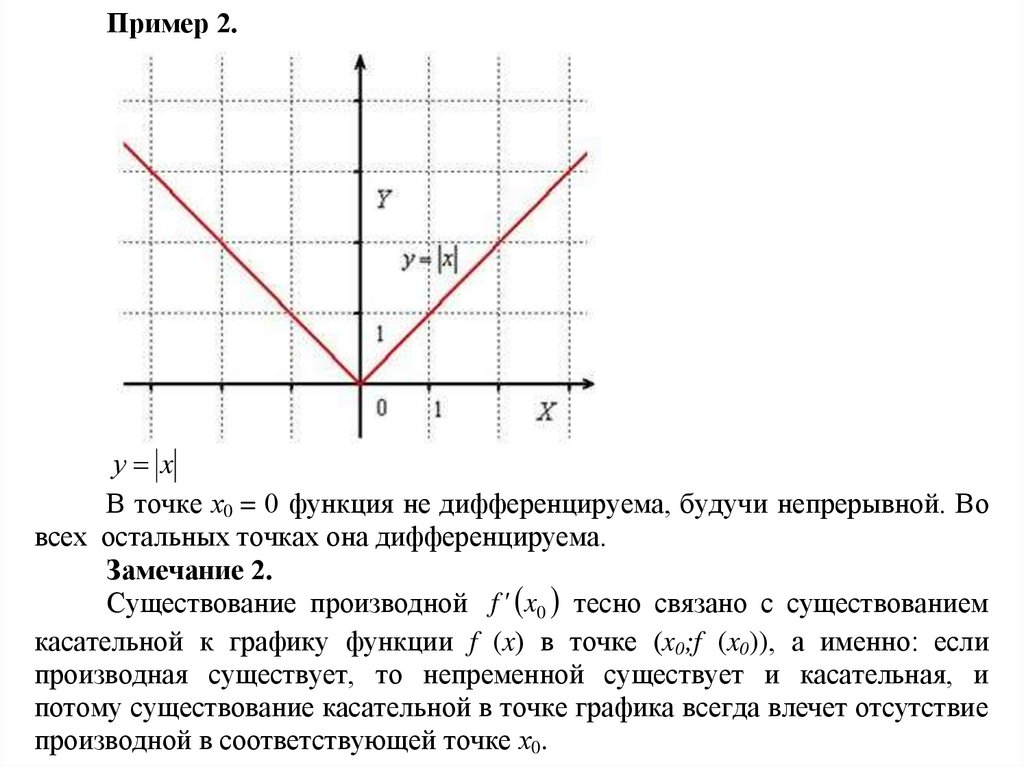
Пример 2.
у x
В точке х0 = 0 функция не дифференцируема, будучи непрерывной. Во
всех остальных точках она дифференцируема.
Замечание 2.
Существование производной f ' x0 тесно связано с существованием
касательной к графику функции f (x) в точке (x0;f (x0)), а именно: если
производная существует, то непременной существует и касательная, и
потому существование касательной в точке графика всегда влечет отсутствие
производной в соответствующей точке х0.