3.05M

Category: $mathematics$ mathematics

Понятие о производной функции её геометрический и физический смысл

1.

Понятие о производной функции, её
геометрический и физический смысл

2.

Начинается урок, он
пойдет студентам в
прок.
Постарайтесь все
понять – аккуратно
все писать.
Долгожданный дан
звонок – начинается
урок

3.

I. Организационный момент
III. Экскурс в историю
IY. Объяснение нового материала
Y. Закрепление нового материала
YI. Подведение итогов
YII. Домашнее задание
YIII.
Рефлексия

«Дифференциальное
исчисление- это описание
окружающего нас мира,
выполненное на
математическом языке.
Производная помогает нам
успешно решать не только
математические задачи, но и
задачи практического
характера в разных
областях
науки и техники»

5.

Denis Diderot
«НАЧИНАТЬ
ИССЛЕДОВАНИЯ МОЖНО
ПО-РАЗНОМУ... ЕСТЬ
ИСТИНЫ, НАИБОЛЕЕ
УДОБНЫЙ ПУТЬ К
КОТОРЫМ СТАНОВИТСЯ
ИЗВЕСТНЫМ ЛИШЬ
ПОСЛЕ ТОГО, КАК МЫ
ИСПРОБУЕМ ВСЕ ПУТИ....
НА ПУТИ К ИСТИНЕ МЫ
ПОЧТИ ВСЕГДА
ОБРЕЧЕНЫ СОВЕРШАТЬ
ОШИБКИ»
Екатерина II

6.

Цель наших совместных
действий
узнать историю возникновения
понятия производной, имена
ученых, которые открыли
производную миру
усвоить понятие производной,
её геометрический и
физический смысл

7.

8.

Приращение аргумента
Приращение функции
Дифференциал функции
Геометрический смысл
Физический смысл
Химический смысл
Экономичекий смысл

9.

– одно из фундаментальных понятий
математики. Оно возникло в XVII веке в связи с
необходимостью решения ряда задач из физики, механики
и математики, но в первую очередь следующих двух:
определение скорости прямолинейного движения и
построения касательной к прямой.

10.

Честь открытия
основных законов
математического
анализа
принадлежит
английскому физику
и математику Исааку
Ньютону и
немецкому
математику, физику,
философу Лейбницу

11.

12.

«Дифференциальное исчисление»

13.

В XIX веке французский
математик О. Коши дал строгое
построение дифференциального
исчисления на основе понятия
предела

14.

О великом Ньютоне!
ввёл понятие
производной,
изучая законы
механики, тем
самым раскрыл
её механический
смысл
Исаак Ньютон (1643-1727)

15.

Операцию отыскания
производной некоторой
функции называют
дифференцированием
функции, а раздел
математики, изучающий
свойства этой операции, дифференциальным
исчислением

16.

Если функция имеет
производную в точке x=a, то
говорят, что она
дифференцируема в этой
точке. Если функция имеет
производную в каждой точке
данного промежутка, то
говорят, что она
дифференцируема на этом
промежутке.

17.

Общее правило нахождения
производной
1. Заданному значению аргумента дают приращение и
вычисляют новое значение функции, соответствующее
новому значению аргумента.
2. Определяют приращение функции, соответствующее
выбранному приращению аргумента.
3. Приращение функции делят на приращение аргумента.
4. Вычисляют предел этого отношения при условии, что
приращение аргумента стремится к нулю.

18.

19.

Определение производной
Производной функции в данной точке
называют предел отношения приращения
функции y к соответствующему приращению
аргумента x при условии, что приращение
аргумента x стремится к 0
∆

20.

В данной функции от икс,
наречённой игреком,
Вы фиксируете икс,
отмечая индексом,
Придаёте вы ему тотчас
приращение,
Тем у функции самой
вызвав изменение.
Приращений тех теперь
взявши отношение,
Пробуждаете к нулю у
дельта икс стремление.
Предел такого отношенья
выясняется,
Он производною в науке
называется!

21.

Пользуясь определением
производной, найдите
производную функции у = 3Х2
1) у+ ∆y= 3(х+ ∆x)2
2) у+ ∆y= 3(x2 +2х ∆x + ∆x2 )=3 x2 +6х ∆x + 3∆x2
3) ∆y = 3 x2 +6х ∆x + 3∆x2 - 3Х2 = 6х ∆x + 3∆x2
4) ∆y/ ∆x = (6х ∆x + 3∆x2 )/ ∆x =6х - 3 ∆x
∆
∆y/ ∆x =∆
6х
(6х - 3 ∆x )
∆∆

22.

Производная суммы двух
функций (f(x) + q(х))' = f' (x) +
q' (x)
/
/
/
(U+V) =U + V
Производная разности двух
функций (f(x) - q(х))' = f' (x) q' (x)
/ =U / - V /
С /= 0
(U-V)
Х/=1
(СX) / = С (СU) / =СU /
(Хn) / = КXn-1

23.

3/ = 0
у(х) = 2х-4
(4х)/ = 4
(Х3) /=3х2 у(х) / = (2х-4 )/ =(2х)/- 4/ =20=2
у(х) = 2х2-4
у(х) / =2(х2)/ - 4/=2*2х=4x
y(x) = x6 – x4 + 2x3 – 3
y(x)/ = (x6 – x4 + 2x3 – 3)/=
=(x6)/ –( x4)/ + (2x3)/– (3)/=6х5-4х3+6х2

24.

Самостоятельно:
найти производные
• у = 2х – 3
•у = х2 – 3х + 4
•у = х3 – 2х2 + 5
•y/ =2
•y/ =2х-3
•y/ =3х2 -4х

25.

«Математическое
Домино»

26.

12x1
23
2хx x
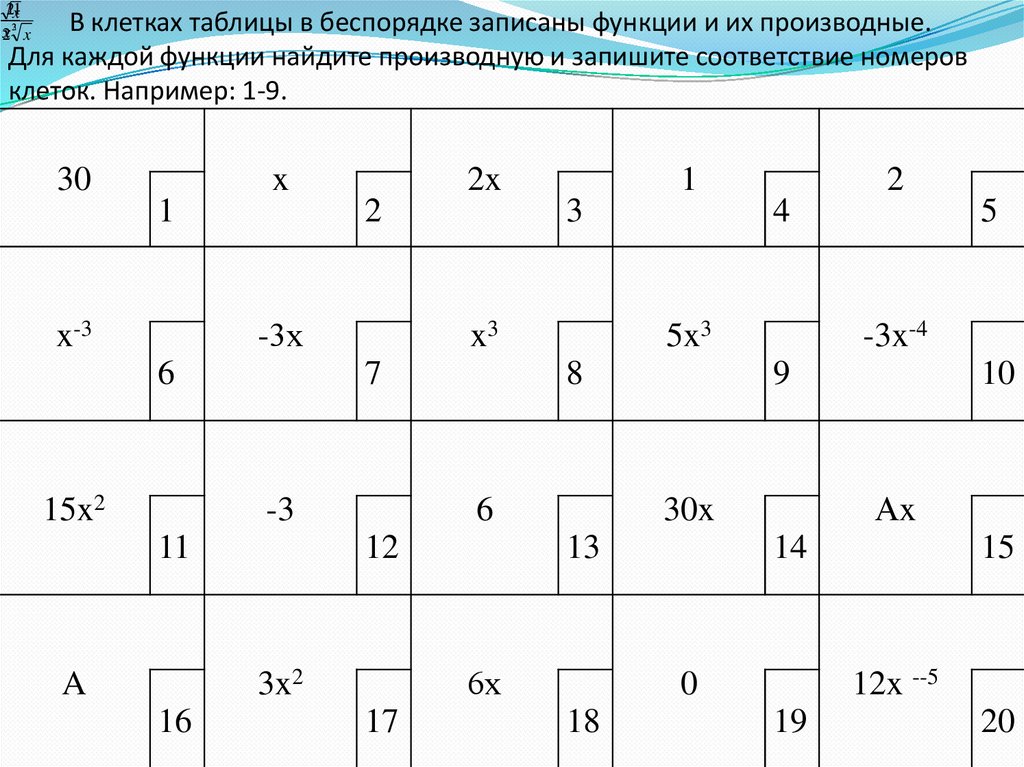
В клетках таблицы в беспорядке записаны функции и их производные.
Для каждой функции найдите производную и запишите соответствие номеров
клеток. Например: 1-9.
30
x
1
x-3
2x
2
15x2
7
-3
11
16
9
13
10
Аx
14
15
12x --5
0
18
5
-3x-4
30x
6х
17
4
8
12
2
5x3
6
3x2
A
3
x3
-3х
6
1
19
20

27.

28.

УстаНазовите соответствие между функцией, записанной в
столбце А, ее схематическим графиком, изображенным в
столбце Б ,производной функции в столбце В и графиком
производной в столбце Г. Например: 1А-5Б-6В-7Г

29.

Карточка - инструкция
Задание: Найдите производную функции у
в точке х=1
y = x2 + 2x; y' = 2x + 2; y'(1) = 4
Инструкция по выполнению задания:
1.Рассмотрите формулу, задающую
функцию, и определите структуру ее правой
части.
2.Найдите производную каждой из
составляющих ее структурных частей.
3.В зависимости от структуры правой части
формулы (сумма или разности) примените
известное правило нахождения производной.
4.Подставте известное значение х в
полученную производную и посчитайте
результат.
5.Запишите ответ

30.

Вариант объяснения решения:
1.Правая часть формулы, задающей
функцию, представляет собой сумму двух
функций:
y = x2 и y = 2x
2.Производная первой функции имеет вид
y′= 2х, a второй y′= 2
3.Применяя правило нахождения
производной суммы, находим производную
заданной функции как сумму найденных
производных:
y′= 2х+2.
4. Производная заданной функции имеет
вид y′(1) =2*1+2=4
5. y′(1) =4

31.

Найдите
производную функции
у в точке x=1
у = 2+5х +x2
а) y = 2 + 5x + x2;
y'=5 + 2x;
y'=5+2*1=7
Ответ: y'(1) = 7

32.

Найдите производную
функции f в точке x=2 .
f(x) = 5х − 6x3
f ' (x) = 5 − 18x2
f ' (2) = 5 − 18*22 = - 67

33.

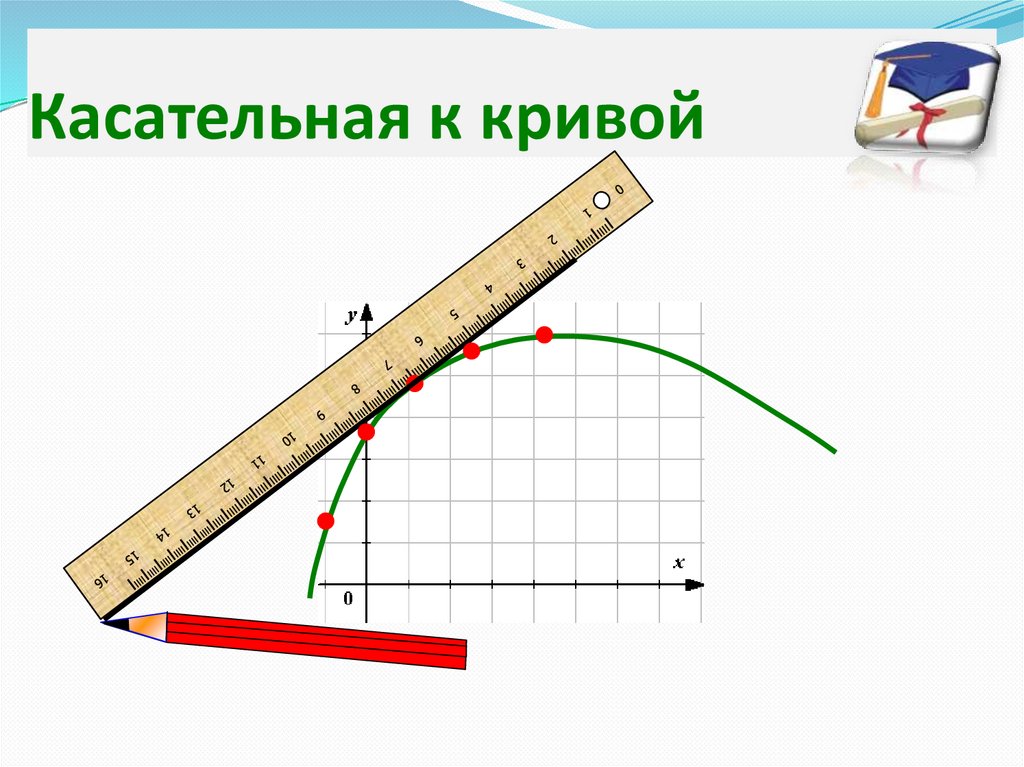
Если продолжить одно из
маленьких звеньев ломаной,
составляющей кривую линию,
то эта продолженная таким
образом сторона будет
называться касательной к
кривой

34.

Лейбниц пришёл к
понятию
производной решая
задачу проведения
касательной к
производной линии,
объяснив этим ее
геометрический
смысл
Г.В.Лейбниц. (1646-1716)

35.

Касательная к кривой

36.

- это угловой коэффициент касательной.
Р1
Р

37.

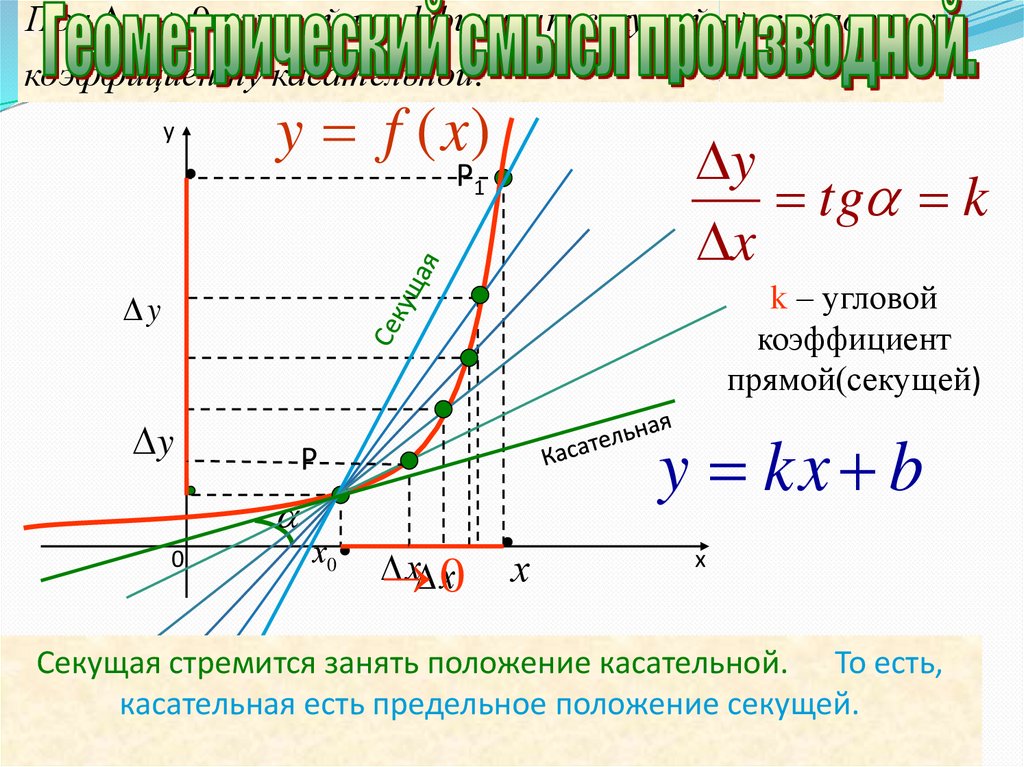
При х 0 угловой коэффициен т секущей к угловому
коэффициен ту касательной.
y
y f (x)
y
tg k
x
Р1
k – угловой
коэффициент
прямой(секущей)
y
y
0
y kx b
Р
х0
х х0
х
х
Секущая стремится занять положение касательной. То есть,
касательная есть предельное положение секущей.

38.

y
y f (x)
y
0
х0
х 0х
х
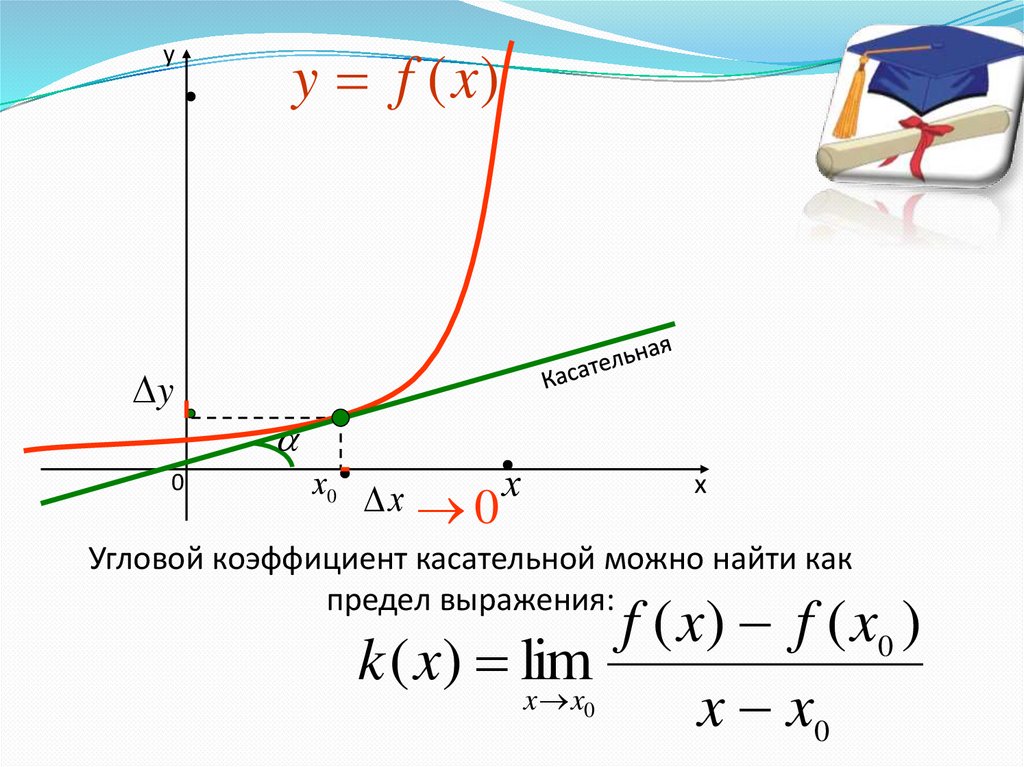
Угловой коэффициент касательной можно найти как
предел выражения:
f ( x ) f ( x0 )
k ( x) lim
x x
x x0
0

39.

y
y f (x)
f ( x ) tg k
y kx b
y
0
х0
х 0х
k – угловой
коэффициент
прямой(касательной)
х
Геометрический смысл производной
Производная от функции в данной точке равна угловому
коэффициенту касательной, проведенной к графику
функции в этой точке.

40.

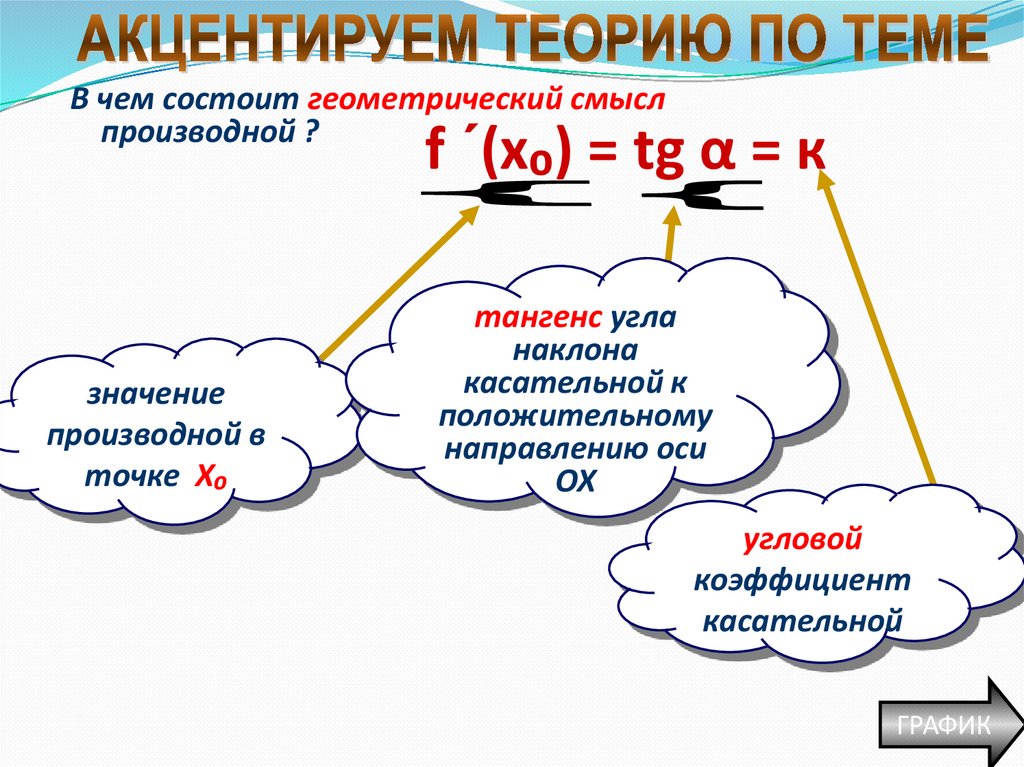
В чем состоит геометрический смысл
производной ?
f ´(x₀) = tg α = к
значение
производной в
точке Х₀
тангенс угла
наклона
касательной к
положительному
направлению оси
ОХ
угловой
коэффициент
касательной
ГРАФИК

41.

42.

43.

Исаак Ньютон
(1643 – 1727)
«Когда величина является
максимальной или
минимальной, в этот
момент она не течет ни
вперед, ни назад.»

44.

Физическийй смысл производной заключается в том, что
производная от координаты по времени есть скорость, а
производная от скорости по времени -ускорение
(t)=x (t)
a(t) = (t)
X-перемещение
-скорость
а –ускорение
t-время

45.

Состав движется по криволинейному
участку железнодорожного пути и
траектория движения задана
формулой: X(t)=2t³+7t². Найдите
скорость в момент t =2 ч
(Перемещение измеряется в
километрах)
Решение:
X(t)=2t³+7t²,
t=2 ч
=x (t)=6t²+14t
(2)=6•22+14•2=24+28=52 км/ч ;

46.

1) «Точка движется по закону: S (t) =2t³-3t²+5t-1 (м), t=5с
Найти: V (t) =? ; а(t)=?»
Все успешно справились с этим заданием. Проверьте и
вы успешность вашего выполнения:
1) V (t ) 6t 2 6t 5 (м/с)
V (5) 6 52 6 5 5 125 (м/с)
a(t ) 12t 6 (м/с 2 )
а(5) 12 5 6 54 (м/с 2 )

47.

1.Находим производную от координаты по времени
(скорость).
2. Подставляем в полученную формулу заданное значение
времени.
3.Находим производную от скорости по времени (ускорение).
4.Подставляем в полученную формулу заданное значение
времени.

48.

Материальная точка движется прямолинейно по закону
X(t)=t³-4t².Найдите скорость и ускорение в момент t =5с
(Перемещение измеряется в метрах)
Решение:
X(t)=t³-4t²,
t=5с
=x (t)=3t²-8t
(5)=3•52-8•5=75-40=35м/с ;
a(t)= (t)=6t-8 ;
a(5)=6•5-8=30-8=22м/с²
Ответ: 35м/с, 22м/с²

49.

х
vср .
t
Δх – перемещение тела
Δt – промежуток времени
в течение которого выполнялось
движение
При t 0 vcр. к мгновенной скорости v(t ),
следовательно, v(t ) S (t ).
S (t ) v(t )
или х (t ) v(t )
f ( х) v( x)
.

50.

Используя
слово
«предел»,
можноможно
сказать,
Используя
слово
«предел»,
что мгновенная скорость в точке t – это
сказать,
что
мгновенная
скорость
в
предел средней скорости при стягивании
точке tна– котором
это предел
средней в точку
отрезка,
она изменяется,
при стягивании
отрезка,
tскорости
или в символической
записи
на котором она изменяется, в точку
t или в символической записи
S (t1 ) S (t )
v(t ) lim
t1 t
t1 t
- это скорость

51.

1. С ее появлением
математика перешагнула
из алгебры в
математический анализ
2. Ньютон назвал ее
«флюксией» и обозначал
точкой
3. Бывает первой, второй,…
4. Обозначается штрихом

52.

УЧЕНЫЙ КОТ

53.

54.

Найти скорость
химической реакции
через 3 секунды.
Если количество
вещества,
вступившего в
химическую реакцию
задается
зависимостью:
р(t) = t2/2 + 3t –3
(моль)
Решение: V(t)=t+3
V(3)=6 м/с

55.

56.

57.

Математика…
выявляет порядок,
симметрию и
определенность,
а это – важнейшие
виды прекрасного.
Аристотель

58.

Почему торжественность
вокруг?
Слышите, как быстро
смолкла речь?
Ты нам, математика,
Это о царице всех наук
даёшь
Заканчиваем мы сегодня
Для победы трудностей
утро.
закалку,
Не случайно ей такой почет.
Учиться с тобой
Это ей дано давать ответы,
молодёжь
Развивать и волю и
Как хороший выполнить
смекалку .
расчет
Для постройки
здания, ракеты.
Есть о математике молва,
Что она в порядок ум
приводит,
Потому хорошие слова
Часто говорят о ней в
народе.
И за то, что в
творческом труде
Выручаешь в трудные
моменты,
Мы сегодня искренне
тебе
Посылаем гром
аплодисментов.

59.

Математика
действительно,
царица наук,
которая не
гнушается выступать
и в роли служанки,
помогающей нам в
покорении вершин
других наук

60.

Что выяснили?
Что сделали?
1. Существует связь между определением
производной и правилами её нахождения с
помощью таблицы;
2. Провели анализ фактов по
существующей связи;
3. Провели обобщение наблюдений;
4. Познакомились с математическими
«портретами»;
5. Познакомились с историзмом проблемы;
6. Наибольшее практическое применение
имеет физический смысл
План
1. Изучить понятие производной;
2. Научиться её применять к
решению различных задач

61.

62.

Домашнее задание.
I. Обязательный минимум:
гл.2 параграф 4 п 12-13,
Найдите производную функции
а) y=2x5-9x20+1;
б) y=4x7 +4x16- 3.
Найдите производную функции f(x)=2x-5x2+3 в точке х=2
Точка движется прямолинейно по закону s(t) =3t242t+3 (s – путь в
метрах, t – время в секундах). Вычислите скорость движения
точки в момент времени t =3c.
II. Задания по выбору:
а) Составить серию вопросов, которые будут контролировать и
дополнять знания по теме «Производная».
б) Составить 5 заданий для самостоятельной работы по теме
«Дифференцирование функции y = f(kx+m)»
в) Задача: Расход электрической энергии электровоза ВЛ 10 ( на
100 км) в зависимости от скорости х км/ч при движении
приблизительно описывается функцией
f(x)=0,0017х²-0,18х+10,2; х>30. При какой скорости расход
электричества будет наименьшим? Найдите этот расход.
III. Задание для интересующихся математикой:
1) Индивидуальное задание: подготовить доклад по теме
следующего урока «Уравнение касательной и нормали»
2) Изучить доказательство вывода формулы «Уравнение
касательной»