Similar presentations:
Синус и косинус. Тема 5
1.
МатематикаПреподаватели:
Мовсисян Геворг Суренович,
Попова Ольга Николаевна
2.
Тема 5.Синус и Косинус
3.
План лекцииВведение.
1. Определение синуса и косинуса.
2. Свойства синуса и косинуса.
3. Знаки тригонометрических
функций.
4. Графики тригонометрических
функций
4.
ВведениеСинус обязан своему
появлению на свет великому
индийскому математику,
астроному Ариабхату (476 –
550 г.н.э.). Он оказал большое
влияние на возникновение
тригонометрии дав точное
5.
В своих работах ученыйназвал синус ардха-джива (ардха
– половина, джива – тетива
лука). Позднее, люди называли
его просто джива. Арабские
математики изучили работу
Ариабхаты, перевели её на
арабский язык, после чего новым
именем синуса стало джайб.
6.
Позже при переводе сарабского на латынь Роберт
Честерский(1145г.) и Герард
Кремонский(1175г.)
употребили слово синус,
которое было буквальным
переводом слова джайб. Синус
(sinus – изгиб, кривизна).
7.
Косинус представляет собойсокращение выражения
complementi sinus, то есть
дополнительный синус.
Его ввёл английский
математик, астроном Эдмунд
Гюнтер в 1620.
8.
Употребляемые намиобозначения впервые применил
Иоган Бернулли в письме к
Леонарду Эйлеру(1739г.).
Эйлер счёл их самыми
удобными.
9.
С помощьютригонометрических функций
описываются соотношения
между сторонами и острыми
углами в прямоугольном
треугольнике.
10.
1. Определение синуса икосинуса.
В прямоугольной системе
координат xOy построим
круг с центром в начале
координат и радиусом
равным единице (R=1).
11.
Опр. Единичную числовуюокружность будем называть
тригонометрическим кругом.
Точки пересечения
окружности и координатных
осей будем называть
узловыми точками.
12.
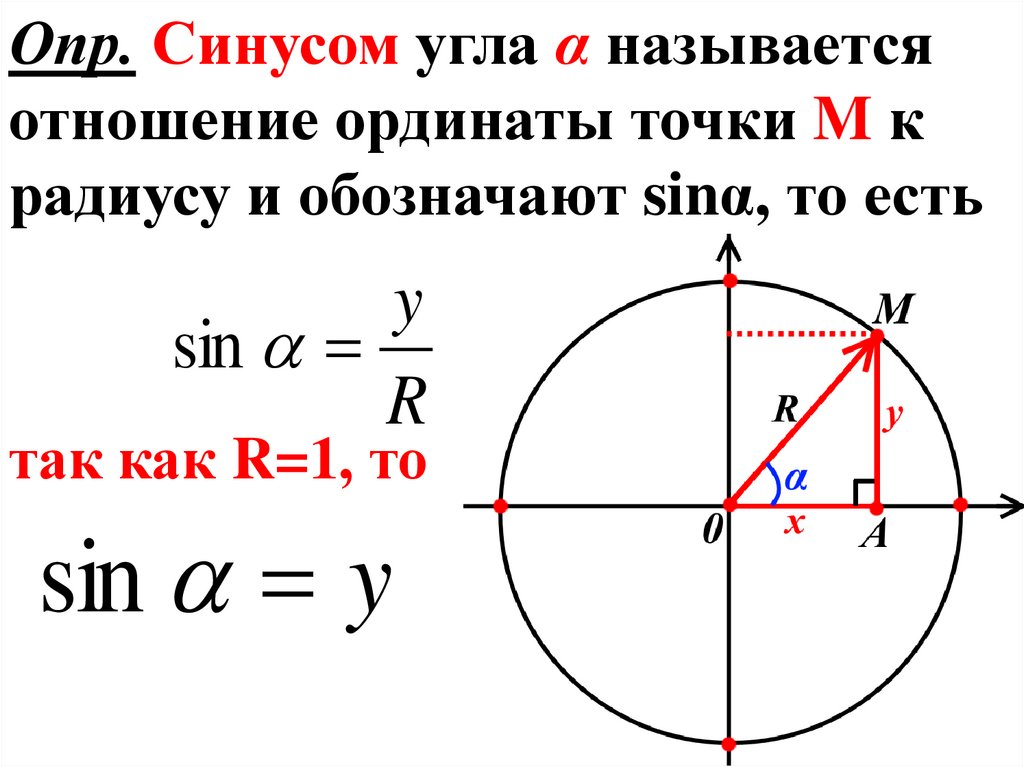
Опр. Синусом угла α называетсяотношение ординаты точки M к
радиусу и обозначают sinα, то есть
y
sin
R
так как R=1, то
sin y
13.
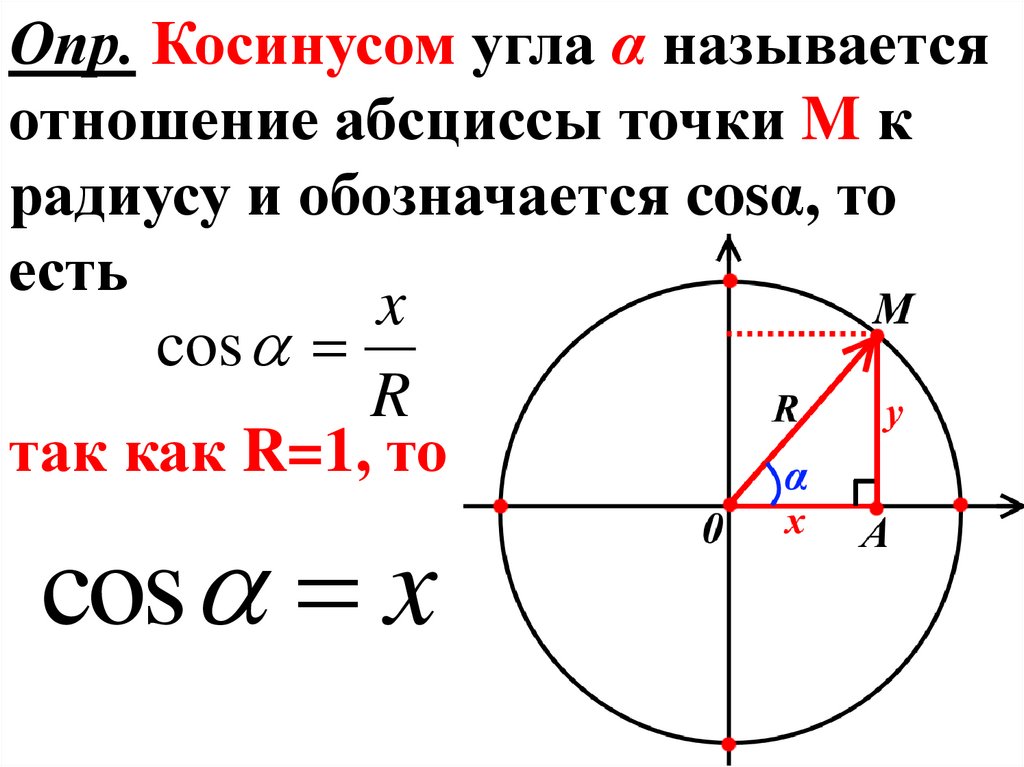
Опр. Косинусом угла α называетсяотношение абсциссы точки M к
радиусу и обозначается cosα, то
есть
x
cos
R
так как R=1, то
cos x
14.
2. Свойства синуса икосинуса.
Функция y=sinα
1.Область определения – все
действительные числа;
2. Область значений – [-1; 1];
3.Функция нечётная sin(-α)=-sinα;
4. Периодичность T=2πn, n ϵ Z;
5. Функция монотонная.
15.
Функция y=cosα1.Область определения –все
действительные числа(D(y)=R)
2. Область значений – [-1; 1];
3. Функция чётная: cos(-α)=cosα;
4. Периодичность T=2πn, n ϵ Z;
5. Функция монотонная.
16.
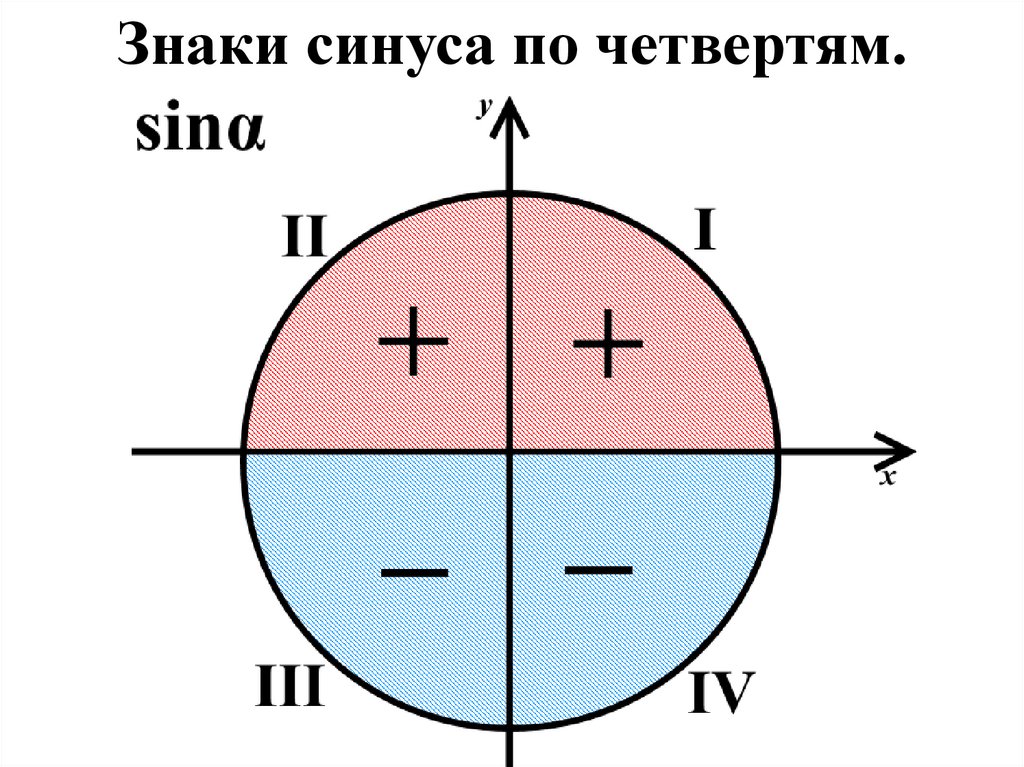
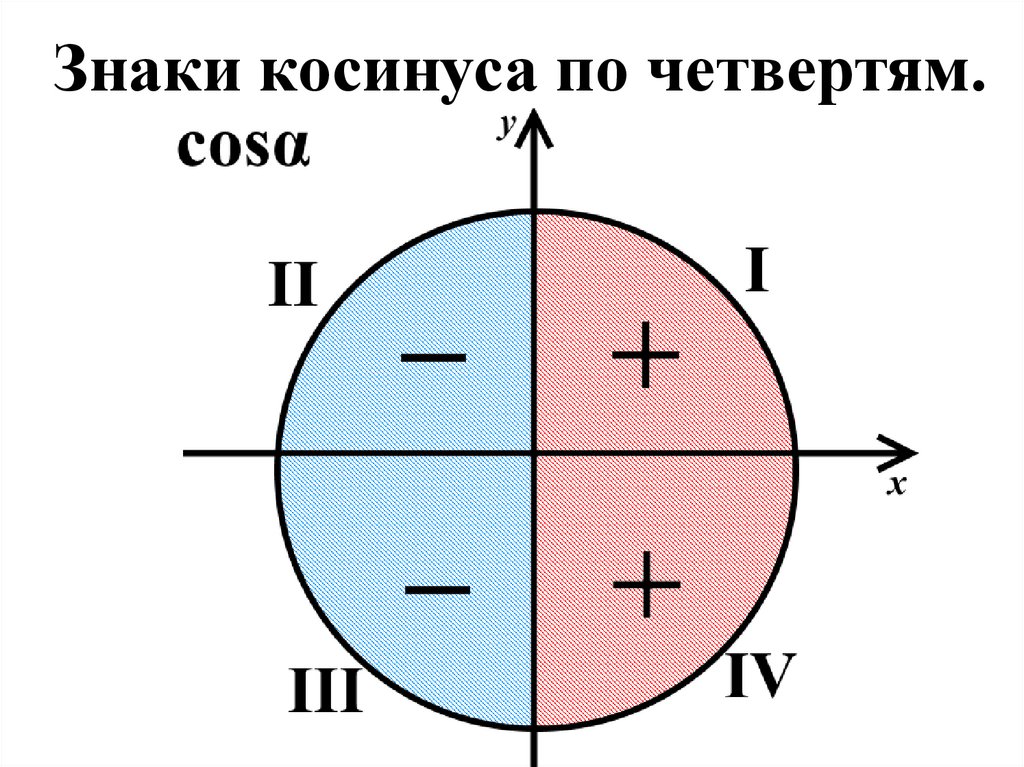
3. Знаки тригонометрическихфункций.
Знак тригонометрической
функции зависит
исключительно от
координатной четверти, в
которой располагается угол α.
17.
Знаки синуса по четвертям.18.
Знаки косинуса по четвертям.19.
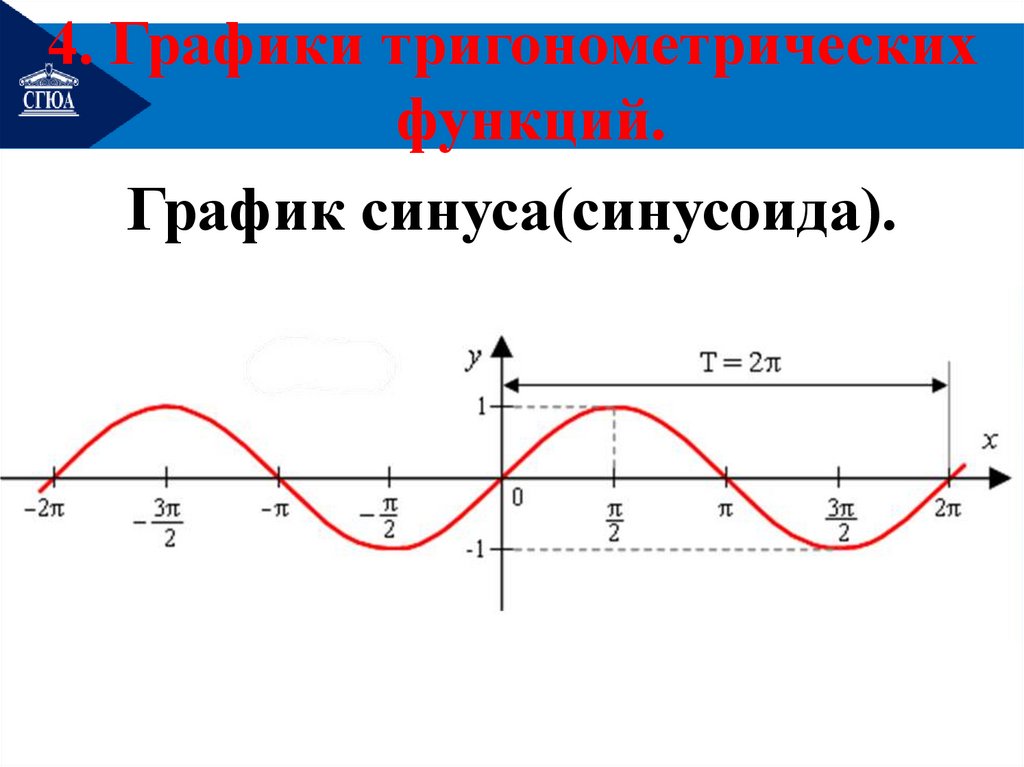
4. Графики тригонометрическихфункций.
График синуса(синусоида).
20.
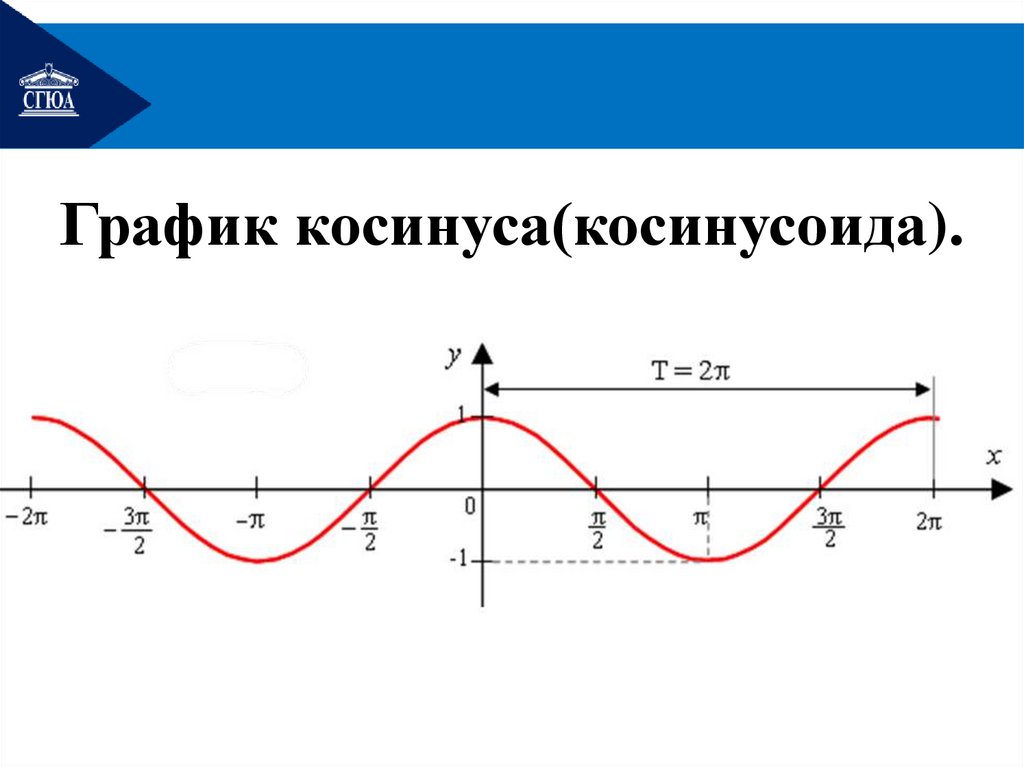
График косинуса(косинусоида).21.
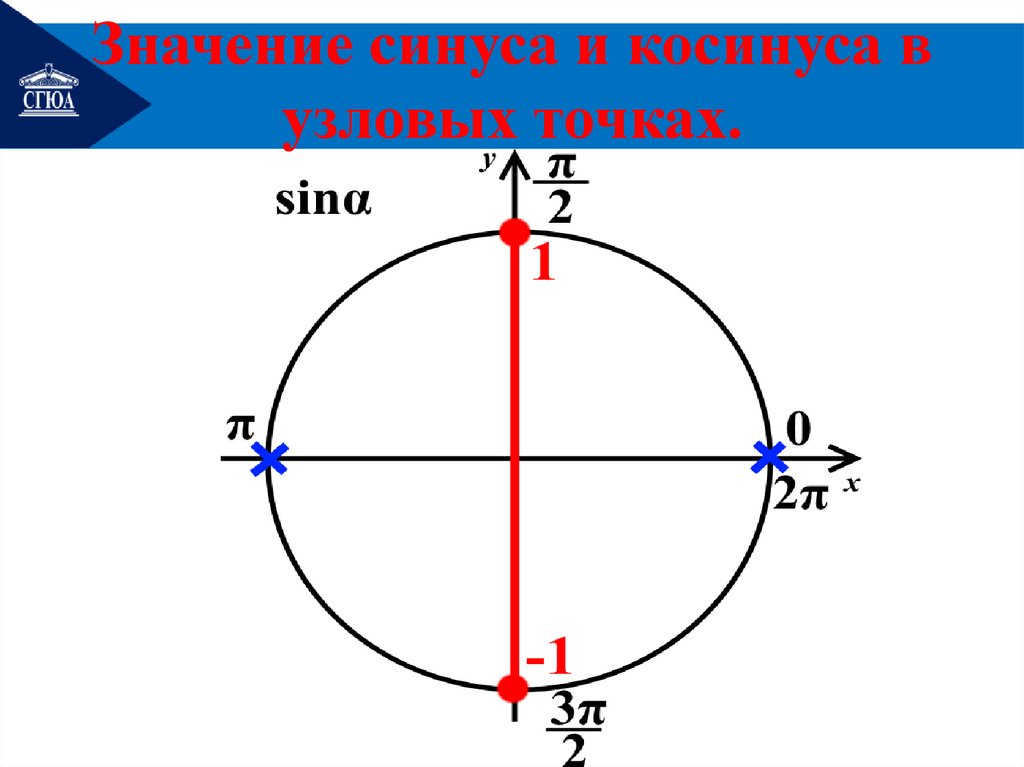
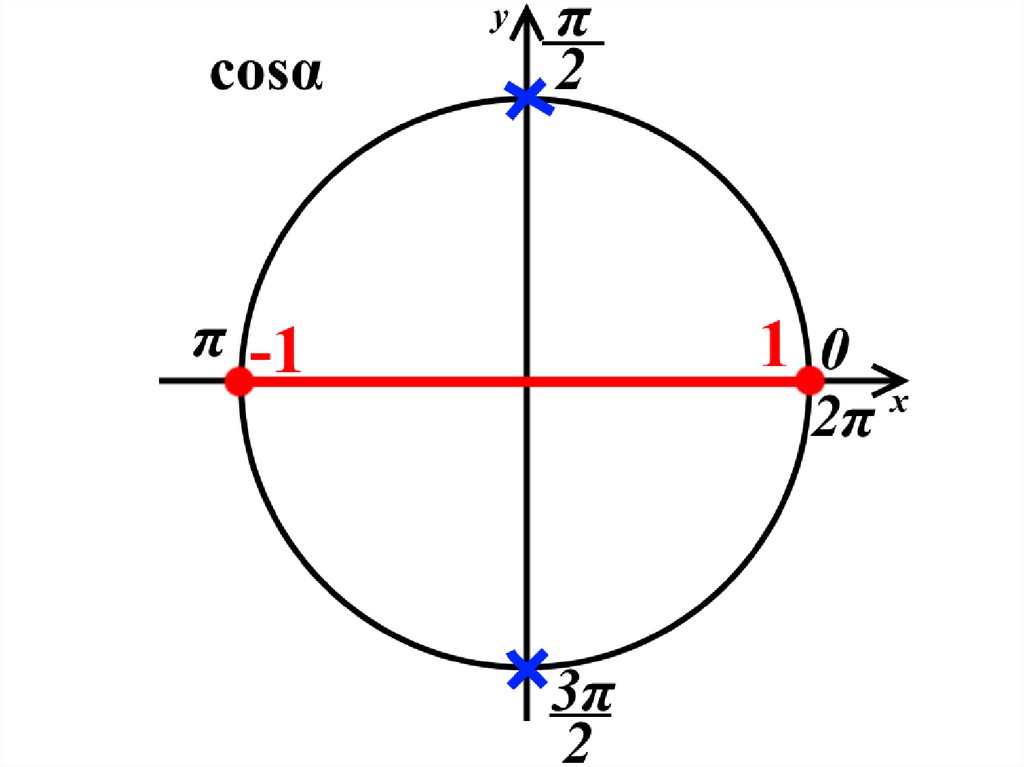
Значение синуса и косинуса вузловых точках.
22.
23.
Значения синуса и косинусауглов I четверти.
24.
Задача.Какое
из
двух
чисел больше:
sin1 или sin2;
cos1 или cos2 ?
25.
Примеры1. Какой знак имеет sin179O , cos206O ?
2. Определить знак выражения
sin190O cos300O.
3. Найти значения выражений:
sin(-30O); cos(-60O).
4. Вычислить: cos420O; sin405O.
26.
Задание для самостоятельногорешения.
1. Какой знак имеет sin359O, cos175 O ?
2. Определить знак выражения
sin288O cos137O.
3. Найти значения выражений :
sin(-45O); cos(-90O)
4.Вычислить: cos390O; sin420O.
27.
СПАСИБО ЗАВНИМАНИЕ!



















 mathematics
mathematics








