Теоремы синусов и косинусов. Урок 5

1. Теоремы синусов и косинусов.

2.

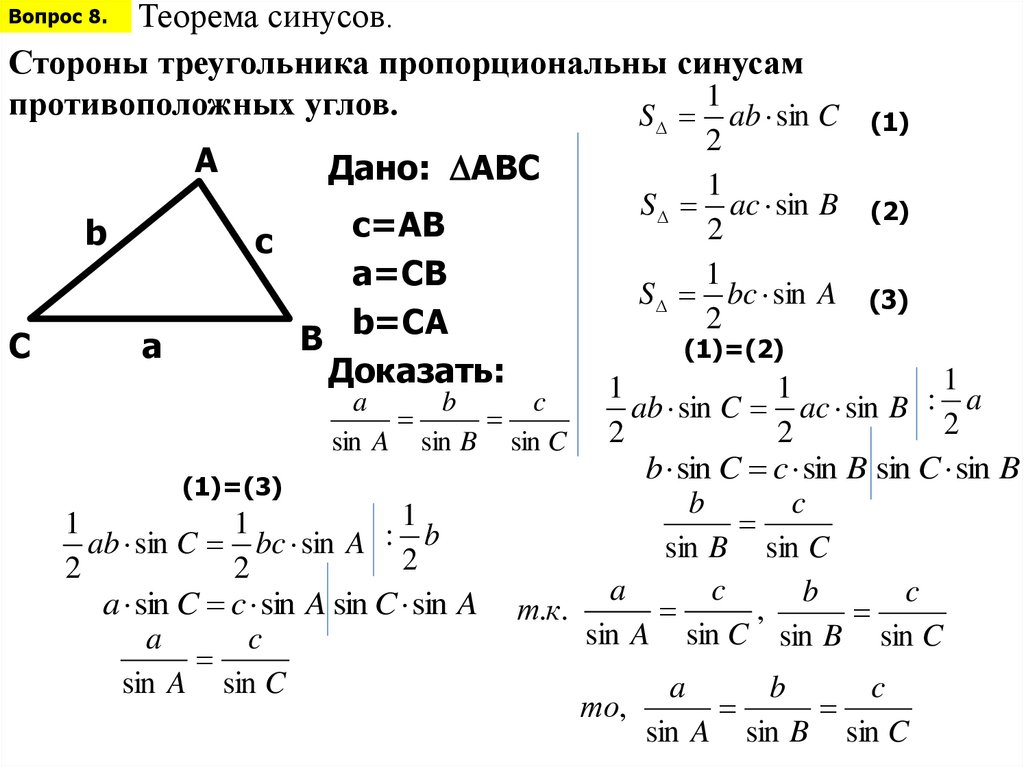
Теорема синусов.
Стороны треугольника пропорциональны синусам
1
противоположных углов.
S ab sin C
Вопрос 8.
A
b
C
Дано: ABC
c
a
c=AB
a=CB
B b=CA
Доказать:
(1)
2
1
S ac sin B (2)
2
1
S bc sin A (3)
2
(1)=(2)
1
1
1
a
b
c
ab sin C ac sin B : a
2
2
sin A sin B sin C 2
b sin C c sin B sin C sin B
(1)=(3)
b
c
1
1
1
ab sin C bc sin A : b
sin B sin C
2
2
2
a sin C c sin A sin C sin A т.к. a c , b c
sin A sin C sin B sin C
a
c
sin A sin C
a
b
c
то,
sin A sin B sin C

3.

a
b
c
2R
sin A sin B sin C
R – радиус описанной окружности.

4. Теорема: Квадрат стороны треугольника равен сумме квадратов двух других сторон, минус удвоенное произведение этих сторон на

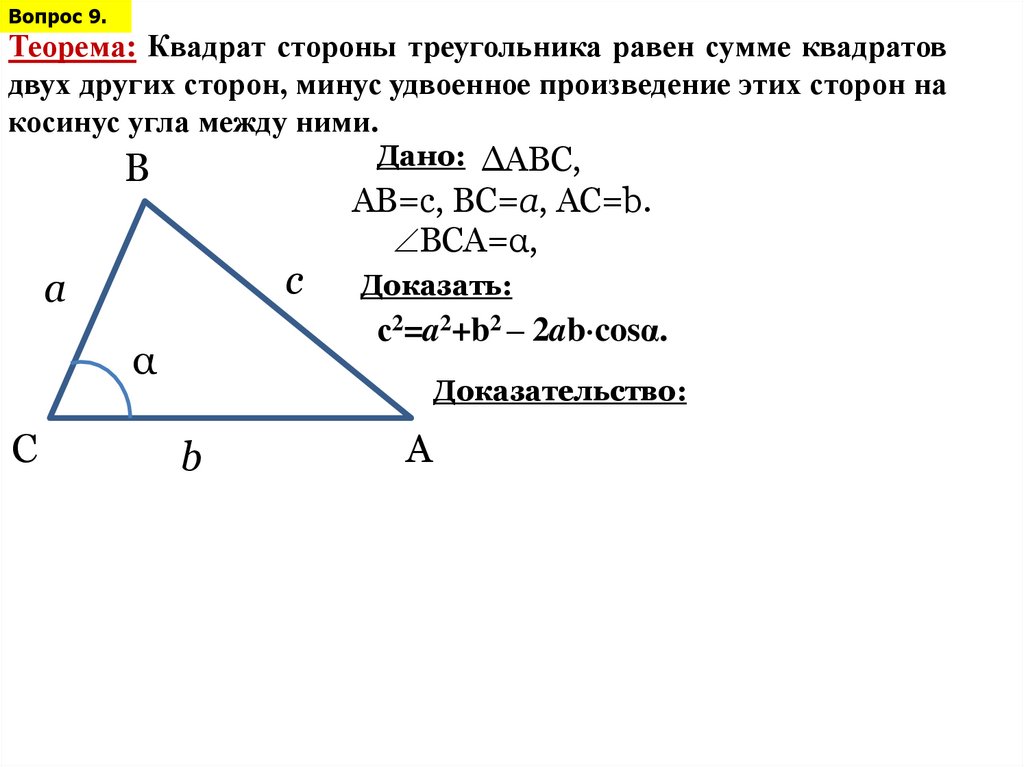
Вопрос 9.
Теорема: Квадрат стороны треугольника равен сумме квадратов
двух других сторон, минус удвоенное произведение этих сторон на
косинус угла между ними.
Дано: ∆АВС,
В
c
a
Доказать:
с2=a2+b2 – 2ab cosα.
α
С
АВ=с, ВС=a, АС=b.
ВСА=α,
Доказательство:
b
А

5. Доказательство:

Доказать:
с2=a2+b2 – 2ab cosα.
у
В
В(a cosα;
a sinα)
a
СВ{a cosα; a sinα}
c
СА{b;0}
Найдем длину вектора АВ :
α
С
С(0;0)
Доказательство:
Найдем координаты
векторов СВ и СА:
b
х
АВ =
А
А(b;0)
AB2=(a cos -b)2+(a sin )2
Доказано.

6.

Домашнее задание:
Вопрос: №1-8
Желаю успехов!