Момент импульса. Лекция №7

1. Лекция № 7 Момент импульса

Алексей Викторович
Гуденко
22/03/2018

2. Лекция №7 Момент импульса

Алексей Викторович
Гуденко
29/03/2018

3. План лекции

Момент импульса частицы и системы частиц
относительно точки и оси. Момент силы.
Уравнение моментов.
Закон сохранения момента импульса для
частицы и системы частиц.
Частица в центральном поле сил.
Примеры решения задач.
Скамья Жуковского.

4. Демонстрации

Движение в поле центральных сил
Скамья Жуковского

5. Момент импульса L = r x p

Момент импульса частицы относительно точки 0
(полюса): L = [rp]
L = prsinθ = pd
d = rsinθ – плечо импульса p относительно точки 0.
p
L = [rp]
r
0
d
p
O
r
θ

6. L = m[r,v] = [r,p]

7. Момент импульса системы частиц

Момент импульса системы частиц относительно
полюса равен сумме моментов импульсов этих частиц
относительно того же полюса:
L = ΣLi = Σ[ripi] = Σmi[ri vi]
L = ∫ρ[r,v]dV
Момент импульса L системы частиц складывается из
её собственного момента импульса L’ в системе
центра масс и момента [rcp], обусловленного
движением системы частиц как целого:
L = L’ + [rcp] (аналог теоремы Кёнига)

8. Доказательство L = L’ + [rcp]

В СЦМ
ri' = ri – rc; vi' = vi – vc →
L' = ∑mi[ri',vi'] = ∑mi[ri – rc,vi – vc] =
∑mi[ri,vi] – ∑mi[ri,vc] – ∑mi[rc,vi] + ∑mi[rc,vc] =
L – [rc,p] →
L = L' + [rc,p] момент импульса системы складывается из
её собственного момента импульса L' и
момента импульса тела [rc,p] как целого.

9. Пример: момент импульса обруча

L = L’ + rpc = mv’r + mv0r = mr2ω + mv0r
Если обруч катится без проскальзывания,
то v’ = ωr = v0:
L = 2mv0r = 2mr2ω

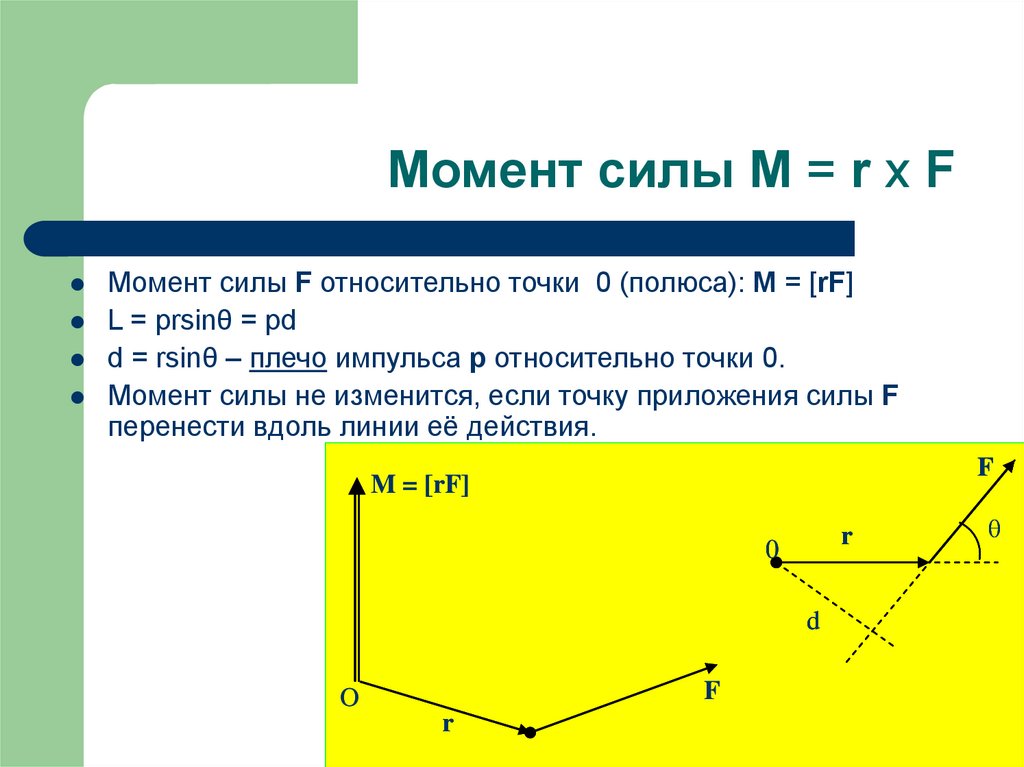
10. Момент силы M = r x F

Момент силы F относительно точки 0 (полюса): M = [rF]
L = prsinθ = pd
d = rsinθ – плечо импульса p относительно точки 0.
Момент силы не изменится, если точку приложения силы F
перенести вдоль линии её действия.
F
M = [rF]
r
0
d
F
O
r
θ

11. Уравнение моментов для частицы и системы частиц

dL/dt = M – скорость изменения момента импульса
частицы равна моменту силы:
dL/dt = [dr/dt,p] + [r,dp/dt] = [r,dp/dt] = [r,F] = M
Для системы частиц:
dL/dt = Mвнешн – производная по времени от момента
импульса системы материальных точек относительно
произвольного неподвижного начала равна
суммарному моменту всех внешних сил относительно
того же начала.
dLz/dt = Mz – уравнение моментов относительно
неподвижной оси 0Z. Если Mz = 0, то Lz = const

12. Закон сохранения момента импульса относительно точки (оси)

Если момент импульса внешних сил
относительно неподвижного начала равен
нулю, то момент импульса системы частиц
относительно того же начала остаётся
постоянным.
Если момент импульса внешних сил
относительно какой либо неподвижной оси
равен нулю, то момент импульса относительно
той же оси остаётся постоянным.

13. Движение частицы в центральном поле сил

Центральная сила зависит только от расстояния r до
силового центра и направлена вдоль r : F = F(r)r/r
Центральная сила не создаёт момента, т.к. плечо
центральной силы относительно центра поля равно
нулю.
В поле центральной силы для частицы L = const.
1.
2.
Траектория частицы – плоская кривая, перпендикулярная L и
проходящая через силовой центр 0.
Секториальная скорость частицы dS/dt = L/2m = const: за
равные промежутки времени радиус-вектор заметает равные
площади (закон площадей).

14. Связь импульса с секториальной скоростью

1.
2.
dS = ½ [rdr] = ½ [rv]dt
σ = dS/dt = ½ [rv] – секторильная
скорость
L =2mσ → σ = L/2m
Если сила, действующая на точку
центральная, то:
Траектория – плоская кривая,
перпендикулярная L и проходит через
силовой центр
За равные промежутки времени
радиус – вектор заметает одинаковые
площади
σ = L/2m = const

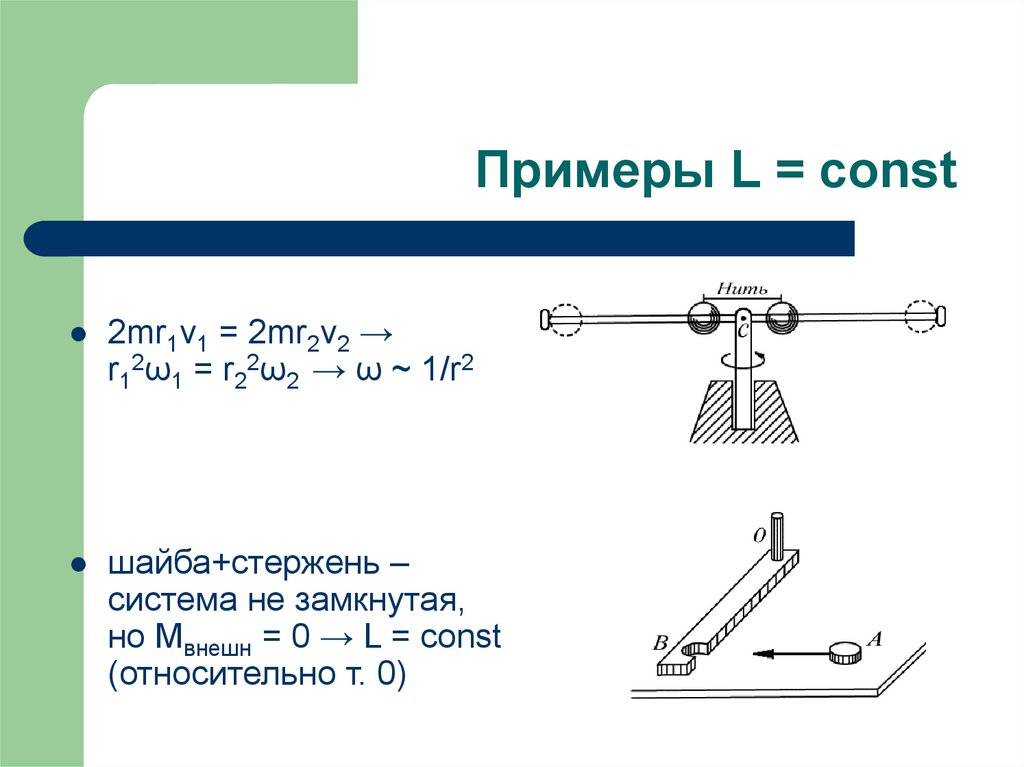
15. Примеры L = const

2mr1v1 = 2mr2v2 →
r12ω1 = r22ω2 → ω ~ 1/r2
шайба+стержень –
система не замкнутая,
но Мвнешн = 0 → L = const
(относительно т. 0)

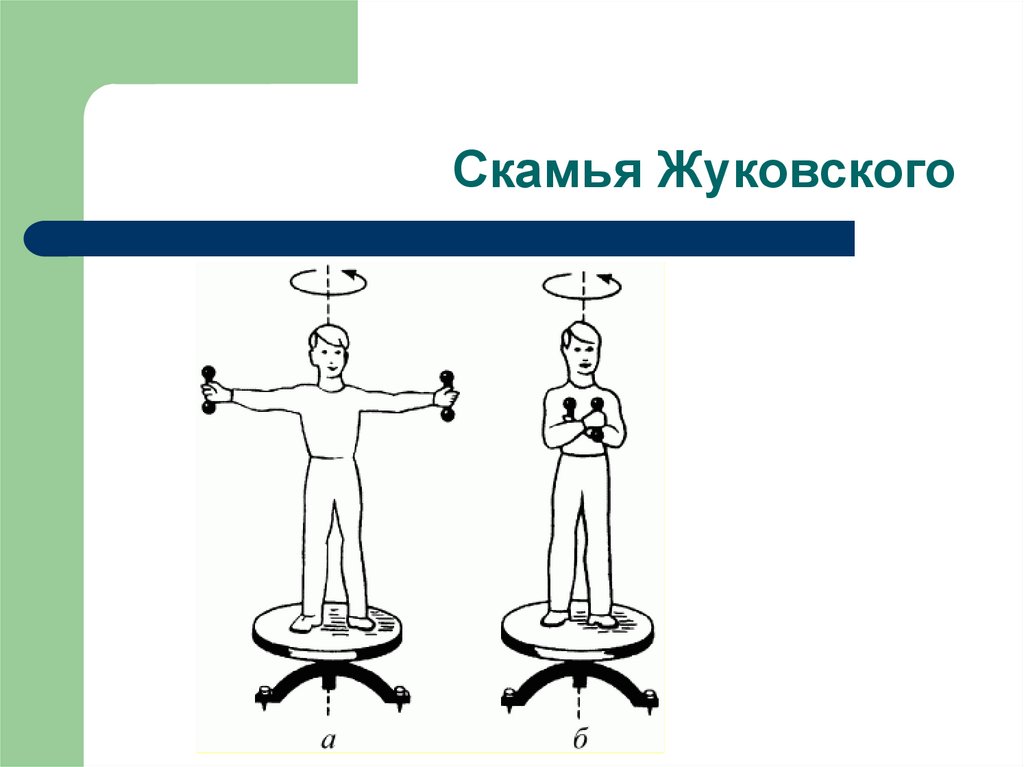
16. Скамья Жуковского

L = const ω2/ω1 = I1/I2 = (I0 + 2mr12)/(I0 + 2mr22)
I0 – момент инерции скамьи+человека без гирь
2mr2 – момент инерции двух гирь

17. Скамья Жуковского

18. Уравнение момента импульса для вращения вокруг неподвижной оси. Момент инерции

При вращении частицы по окружности момент её импульса
относительно центра окружности: L = mrv = mr2ω
Для системы частиц Lz = Σmir2ω = Izω
Iz – момент инерции системы относительно оси z равен сумме масс
частиц на квадраты расстояний до оси z:
Iz = Σmir2
При вращении твёрдого тела вокруг неподвижной оси (z) проекция
момента её импульса на ось вращения равна произведению
момента инерции тела относительно оси вращения на угловую
скорость: Lz = Izω
Основное уравнение динамики вращательного движения
относительно неподвижной оси:
d(Izω)/dt = Mz
Если момент внешних сил M относительно оси вращения равен
нулю (Mz = 0), то Lz сохраняется:
Lz = Izω = const

19. Пульсар – быстро вращающийся объект: T = 10-3 - 1 c

Плотность вещества ρ ~ 1014 г/см3 – (плотность
ядерного вещества)
Плотность Солнца ρ0 ~ 1,4 г/см3
Период обращения Солнца T0 = 25,5 суток.
Если Солнце сожмётся до пульсара, то период
его вращения будет:
T ≈ T0(ρ0/ρ)2/3 = 1,3 10-3 с = 1,3 мс. ν ~ 1000 об/с (!)
Радиус такого пульсара r ~ 18 км

20. Задача на законы сохранения импульса, момента импульса и энергии замкнутой системы (№ 6.7)

l
O
V0
l
Закон сохранения импульса:
mv0 = mv + 3mvc
Закон сохранения момента импульса относительно O:
0 = 0 + L’ + ℓpc = - 2mv’ℓ + 3mvc,, v’ = ωℓ
Закон сохранения энергии:
½mv02 = ½ mv2 + ½ (3m)vc2 + 2 (½ mv’2)
Ответ:
v1 = -2v0/11; v2 = vc = 4v0/11; v3 = +10v0/11; v = - v0/11;
ω = v’/ℓ = 6v0/11ℓ

21. Поступательное и вращательное (вокруг оси z) движения

Поступательное движение
Вращательное движение
v – линейная скорость
a = dv/dt – линейное
ускорение
m – масса
p = mv – импульс
F - сила
dp/dt = ma = mdv/dt = F
K = mv2/2 = p2/2m
dA = Fsds
ω – угловая скорость
ε = dω/dt – угловое ускорение
Iz – момент инерции
относительно оси вращения
Lz = Izω – проекция момента
импульса на ось вращения
Mz – момент силы отн. z
dLz /dt = Izε = Izdω/dt = Mz
K = Izω2/2 = Lz2/2Iz
dA = Mzdφ

22. Условие равновесия твёрдого тела

Тело будет оставаться в покое, если:
1. Равнодействующая всех сил,
приложенных к телу, равна нулю:
F = ΣFi = 0
2. Суммарный момент сил относительно
любой точки равен нулю:
M = ΣMi = 0