Similar presentations:
Закон сохранения момента импульса
1. Лекция 3-2021 Закон сохранения момента импульса
• Момент силы• Момент импульса материальной точки (МТ)
и механической системы (МС)
• Уравнение моментов механической
системы
• Закон сохранения момента импульса МС
А.С. Чуев. 2022 г.
1
2.
Мир – прекрасная книга, но бесполезная длятого, кто не умеет читать
К. Гельвеций
Во вращательном движении, особенно
вихревом, целое первее частей и это
роднит его со строением живого.
А.С. Чуев. 2022 г.
2
3. Определение вектора момента силы относительно точки
Размерность: ML2T-2Единица измерения: Н·м
А.С. Чуев. 2022 г.
3
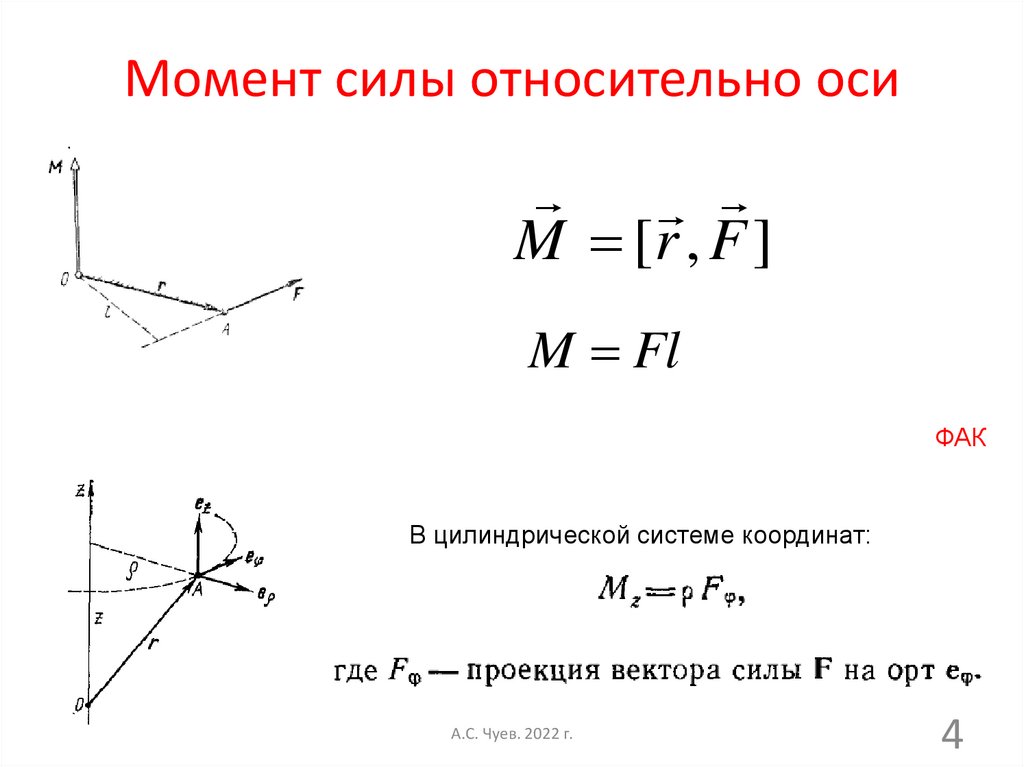
4. Момент силы относительно оси
M [r , F ]M Fl
ФАК
В цилиндрической системе координат:
А.С. Чуев. 2022 г.
4
5. Закон сохранения момента импульса
• в инерциальной системе отсчета моментимпульса замкнутой системы частиц
остается постоянным, т.е, не меняется
со временем
А.С. Чуев. 2022 г.
5
6. Определение вектора момента импульса относительно точки
[L] = кг·м2/сdim L = ML2T-1
Уравнение моментов
А.С. Чуев. 2022 г.
6
7.
Представляет собой скорость, которая совпадаетпо направлению с вектором импульса, тогда:
Тогда
Используя
получим:
- момент силы.
Уравнение моментов:
Если
А.С. Чуев. 2022 г.
то
7
8.
dL внешM
dt
Это основной закон динамики
вращательного движения твердого тела,
вращающегося вокруг точки.
L
Момент импульса системы
является основной
динамической характеристикой вращающегося
тела.
Момент импульса – сохраняющаяся и
квантуемая физическая величина
А.С. Чуев. 2022 г.
8
9. Закон сохранения момента импульса
суммарный момент всех внутренних силотносительно любой точки равен нулю
производная момента импульса системы
по времени равна суммарному моменту
всех внешних сил
суммарный момент всех внешних сил
А.С. Чуев. 2022 г.
9
10.
Li ri , mi vi .i
L x
j k
y
z r , p .
p x p y pz
L трехмерный момент импульса относительно центра
вращения О.
А.С. Чуев. 2022 г.
10
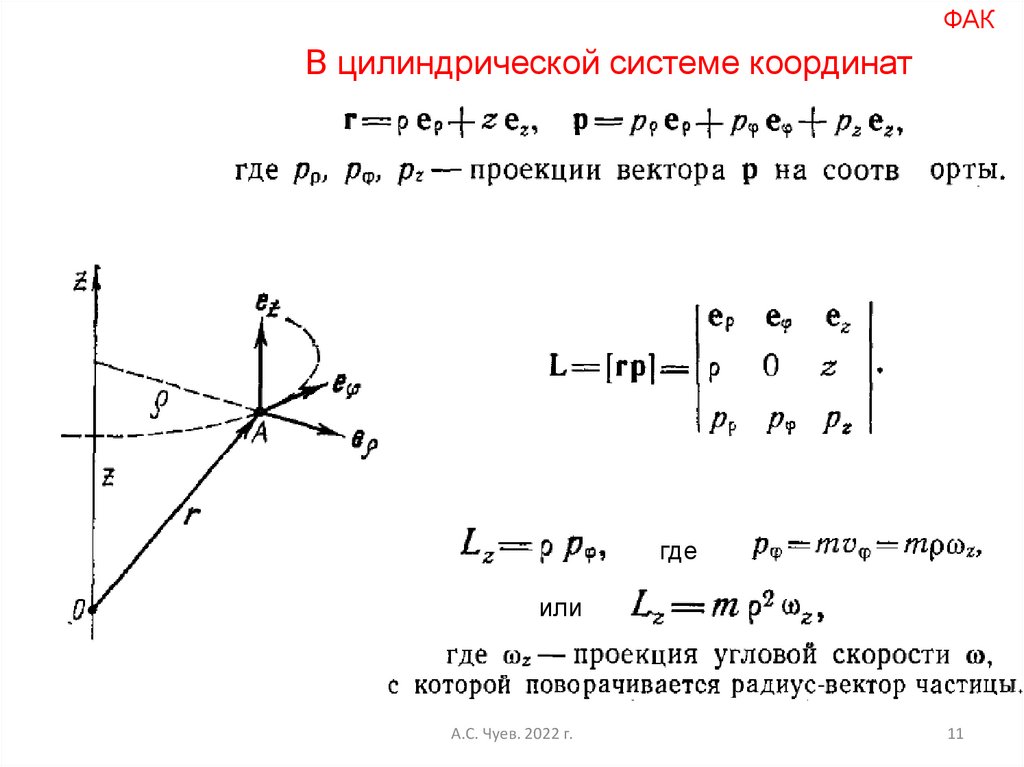
11.
ФАКВ цилиндрической системе координат
где
или
А.С. Чуев. 2022 г.
11
12. Динамика вращательного движения твердого тела относительно оси
Движение твердого тела относительнонеподвижной точки является основным
видом
движения. Однако вычислить вектор L – момент
импульса системы относительно произвольной
точки сложно: надо знать шесть проекций (три
задают положение тела, три задают направление
силы или скорости).
Значительно проще определяется момент
импульса тела, вращающегося вокруг
неподвижной оси (z).
А.С. Чуев. 2022 г.
12
13.
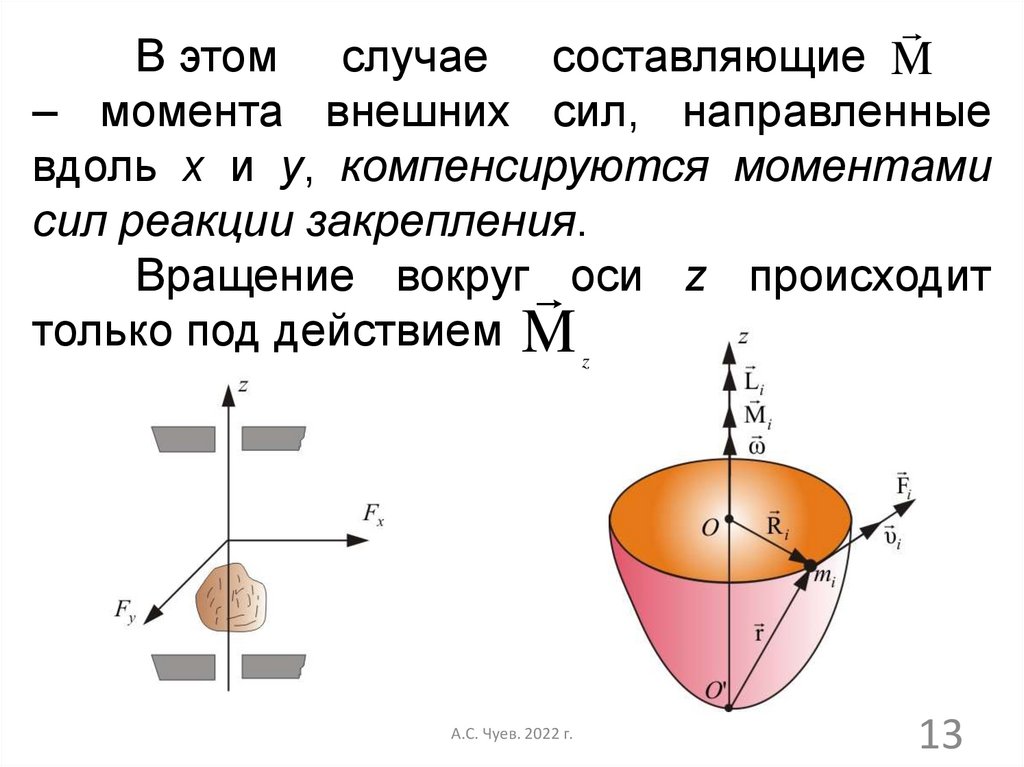
составляющие MВ этом случае
– момента внешних сил, направленные
вдоль x и y, компенсируются моментами
сил реакции закрепления.
Вращение вокруг оси z происходит
только под действием M z
А.С. Чуев. 2022 г.
13
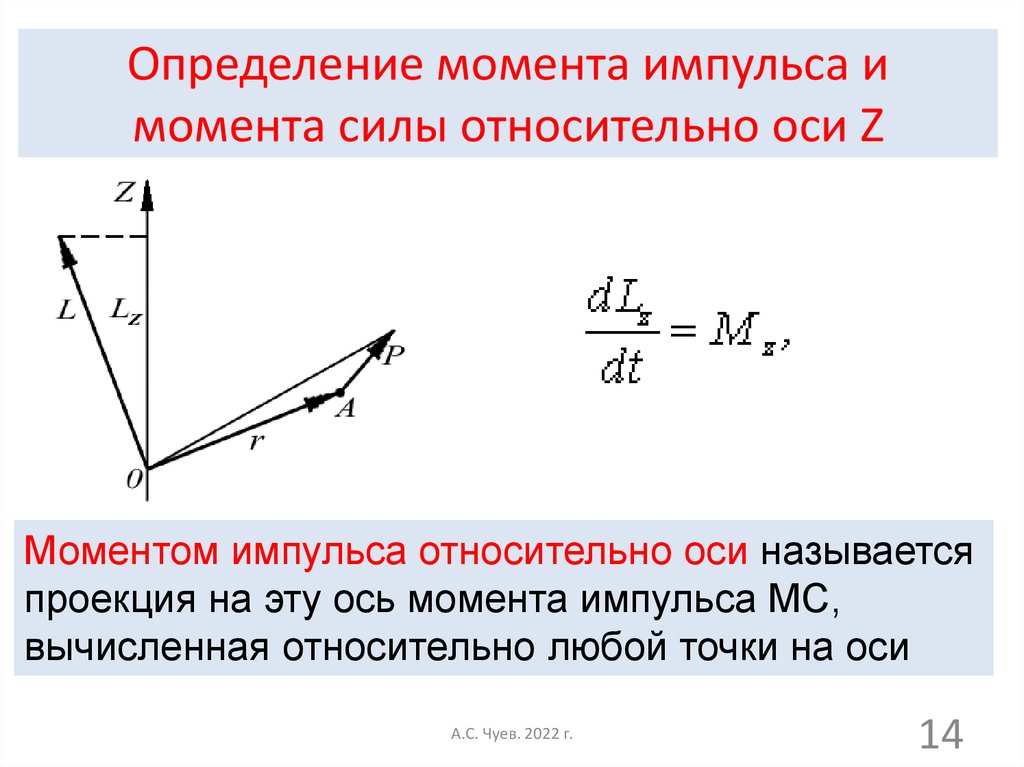
14. Определение момента импульса и момента силы относительно оси Z
Моментом импульса относительно оси называетсяпроекция на эту ось момента импульса МС,
вычисленная относительно любой точки на оси
А.С. Чуев. 2022 г.
14
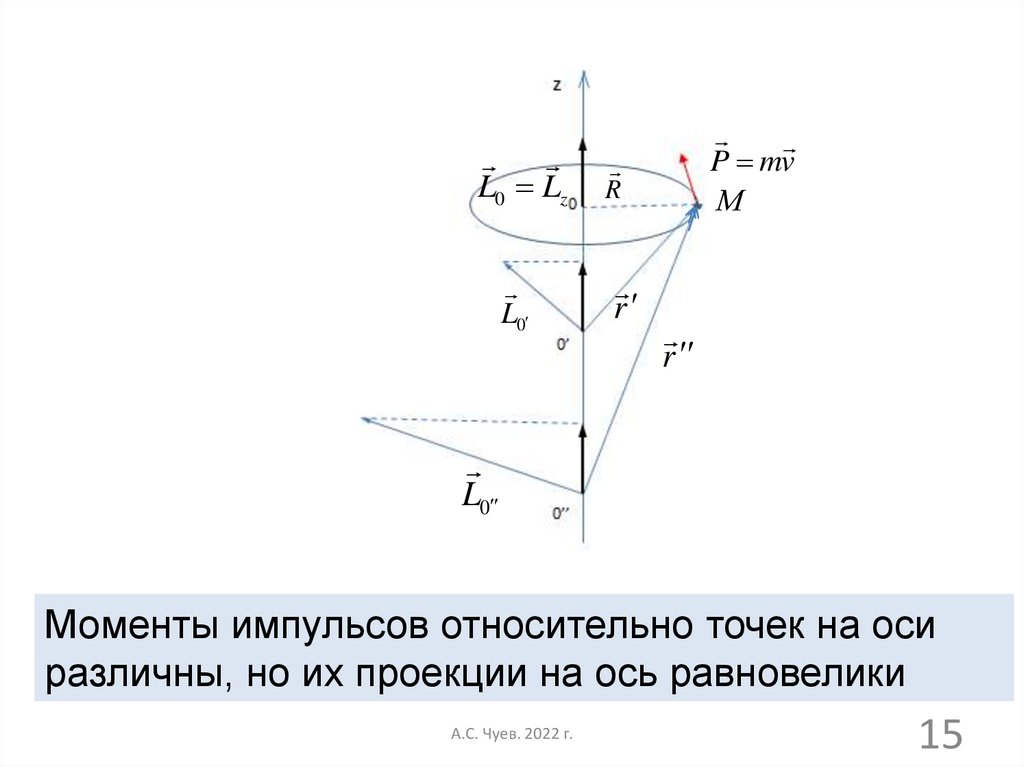
15.
L0 LzL0
P mv
М
R
r
r
L0
Моменты импульсов относительно точек на оси
различны, но их проекции на ось равновелики
А.С. Чуев. 2022 г.
15
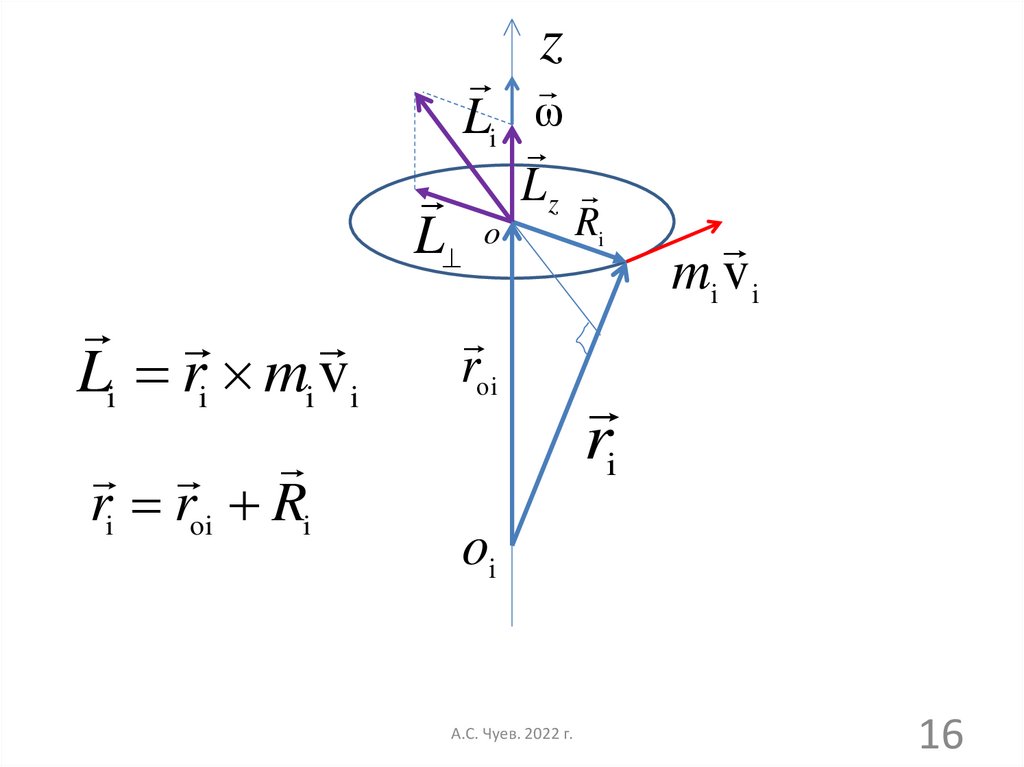
16.
zL
Li ri mi vi
ri roi Ri
Li ω
Lz
o
roi
Ri
mi v i
ri
oi
А.С. Чуев. 2022 г.
16
17.
Li ri mi vi [roi mvi ] [ Ri mvi ] L z Lziтак как L
не зависит от выбора точки oi , то
zi
Lzi Ri mi vi [mi Ri ω Ri ]
(применяя правило«бац-цаб»), получаем:
2
Lzi mi ω( Ri Ri ) mi Ri ( Ri ω) mi Ri ω
А.С. Чуев. 2022 г.
17
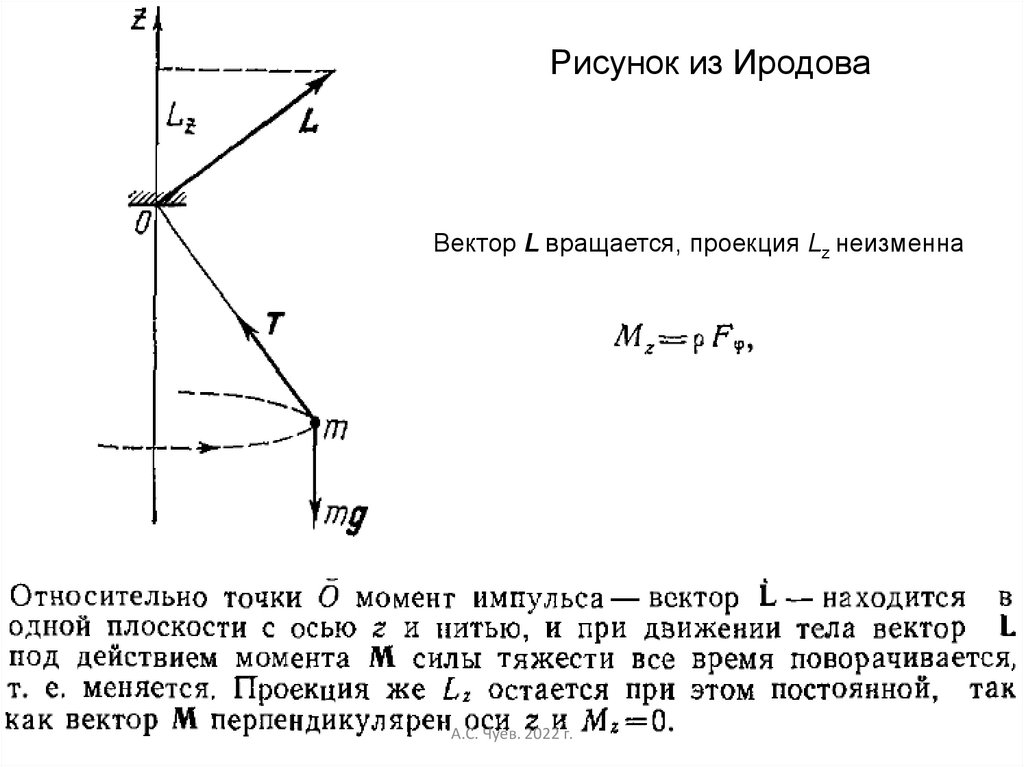
18.
Рисунок из ИродоваВектор L вращается, проекция Lz неизменна
А.С. Чуев. 2022 г.
18
19. Демонстрационный опыт с шарами
А.С. Чуев. 2022 г.19
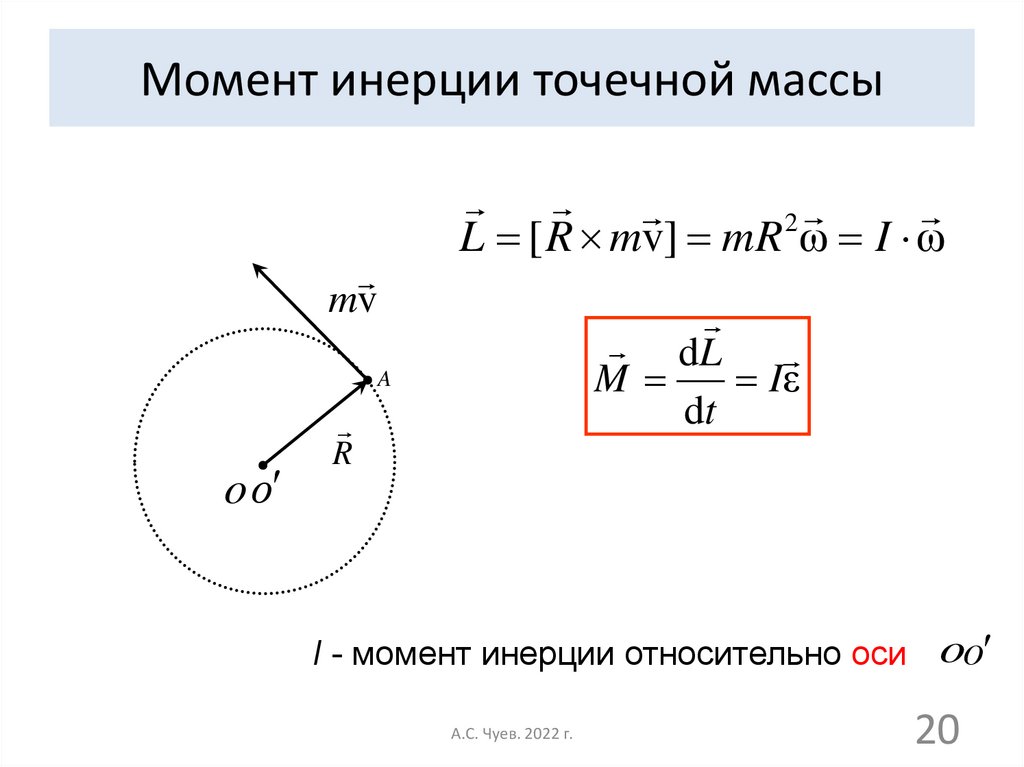
20. Момент инерции точечной массы
2L [ R mv] mR ω I ω
mv
dL
M
Iε
dt
A
o о
R
I - момент инерции относительно оси
А.С. Чуев. 2022 г.
oо
20
21. Центр масс (инерции) твёрдого тела
yС
rC
r dm
m
dm
ρ r dV
V
m
m
x
А.С. Чуев. 2022 г.
21
22. Момент инерции твердого тела относительно оси
Ari
I mi ri
mi
2
B
dim I = ML2
А.С. Чуев. 2022 г.
[I] = кг·м2
22
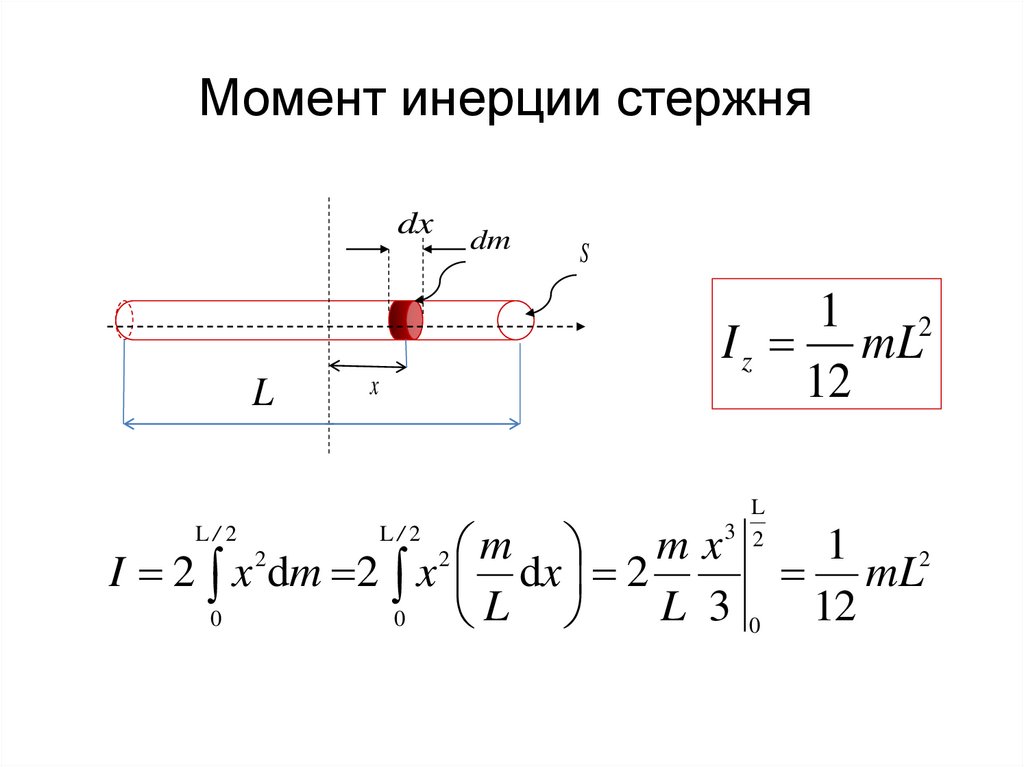
23.
Момент инерции стержняdx
L
dm
S
1
2
I z mL
12
x
L
3 2
mx
m
I 2 x dm 2 x dx 2
L 3
L
0
0
L/ 2
L/ 2
2
2
0
1
mL2
12
24.
Момент инерции дискаdr
h
r
R
mR2
Iz
2
1
2m 3
2
2 m
I r dm r 2 2πr h dr 2 r dr mR2
2
R h
R 0
0
0
R
R
R
А.С. Чуев. 2022 г.
24
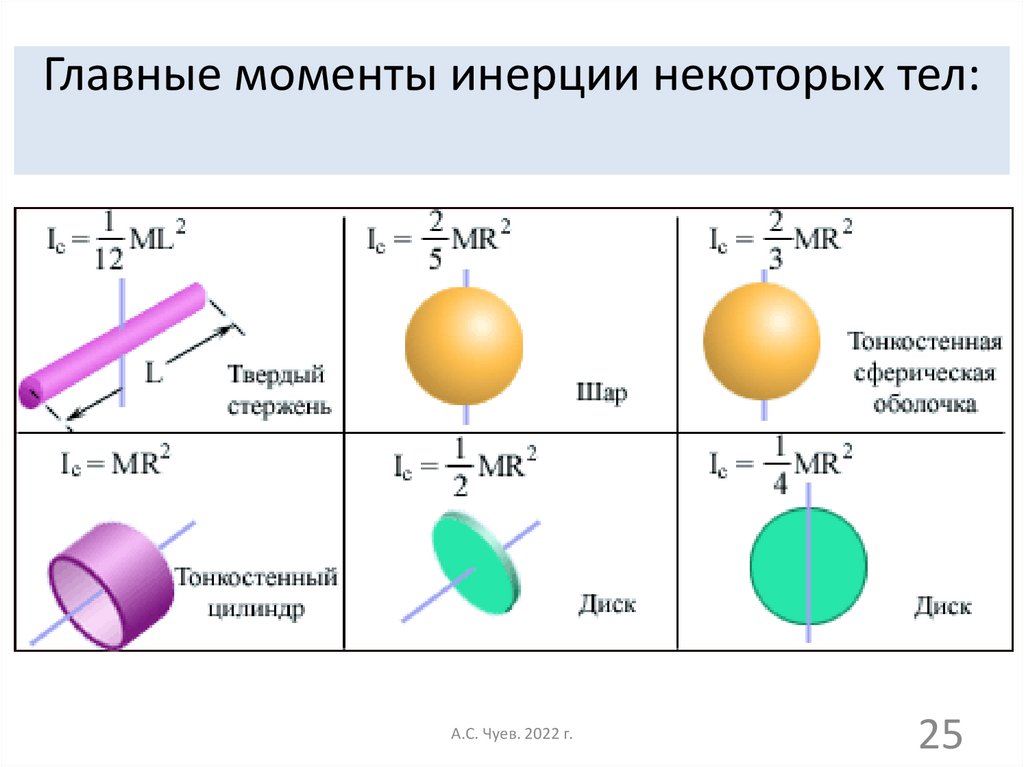
25. Главные моменты инерции некоторых тел:
А.С. Чуев. 2022 г.25
26.
Теорема ШтейнераI I c md
Момент инерции тела
I
2
относительно
любой оси вращения равен моменту его
инерции I c относительно параллельной
оси, проходящей через центр масс С тела,
плюс произведение массы тела на
квадрат расстояния между осями.
26
А.С. Чуев. 2022 г.
27.
I r 2 dmr
dm
R
m
о
d
c
r d R
r d 2 d R R2
2
2
I d dm 2 d R dm R 2 dm
2
d const
При
2
I d dm 2 d R dm R dm
m
m
m
2
m
Отсюда:
учитывая, что:
m
I m d 2 IC
dm m,
m
m
R dm 0,
m
А.С. Чуев. 2022 г.
R
m
2
dm I C
27
28.
Пример: стержень массойm, длиной l, вращается
вокруг оси, проходящей
через конец стержня.
1 2
I c ml
12
2
1 2 1 2 1 2
l
I z I c m ml ml ml .
4
3
2 12
А.С. Чуев. 2022 г.
28
29.
А.С. Чуев. 2022 г.29
30.
А.С. Чуев. 2022 г.30
31. Динамика вращательного движения твердого тела
Во вращательном движениимомент инерции играет роль массы
ma F )
(Сравним:
–
основное
уравнение
поступательного движения тела).
динамики
Iε M
А.С. Чуев. 2022 г.
31
32.
Просуммировав по всем i-тымточкам, получим:
dω
I
M
dt
или
Iε M
Это основное уравнение динамики тела,
вращающегося вокруг неподвижной оси.
(варианты представления этого уравнения)
Idω Mdt;
Idω dL;
А.С. Чуев. 2022 г.
L Iω
32
33.
Осьвращения,
направление
которой
в
пространстве остается неизменным без действия
на нее каких-либо сил извне, называют свободной
осью тела.
В общей теории доказывается, что для любого
твердого тела существуют
три взаимно перпендикулярные оси, проходящие
через центр масс тела, которые могут служить
свободными осями. Их называют главными осями
инерции тела.
А.С. Чуев. 2022 г.
33
34.
Важной особенностью главных осей инерции телаявляется то, что при вращении тела вокруг любой
из них момент импульса тела совпадает по
направлению с угловой скоростью тела и
определяется формулой:
L I
Если тело обладает осью симметрии, например, однородный
цилиндр, то одной из его главных осей инерции является ось
симметрии, в качестве же остальных осей могут служить две
любые взаимно перпендикулярные оси, лежащие в
плоскости, перпендикулярной оси симметрии и проходящей
через центр инерции тела.
А.С. Чуев. 2022 г.
34
35.
Работа при вращательном движенииd A Md
Размерность момента силы = размерности работы
А.С. Чуев. 2022 г.
35
36. Пример
ФАКПример
2F
z
mR
2 Ft
Угловая частота вращения: (t ) z (t ) (0)
mR
А.С. Чуев. 2022 г.
36
37.
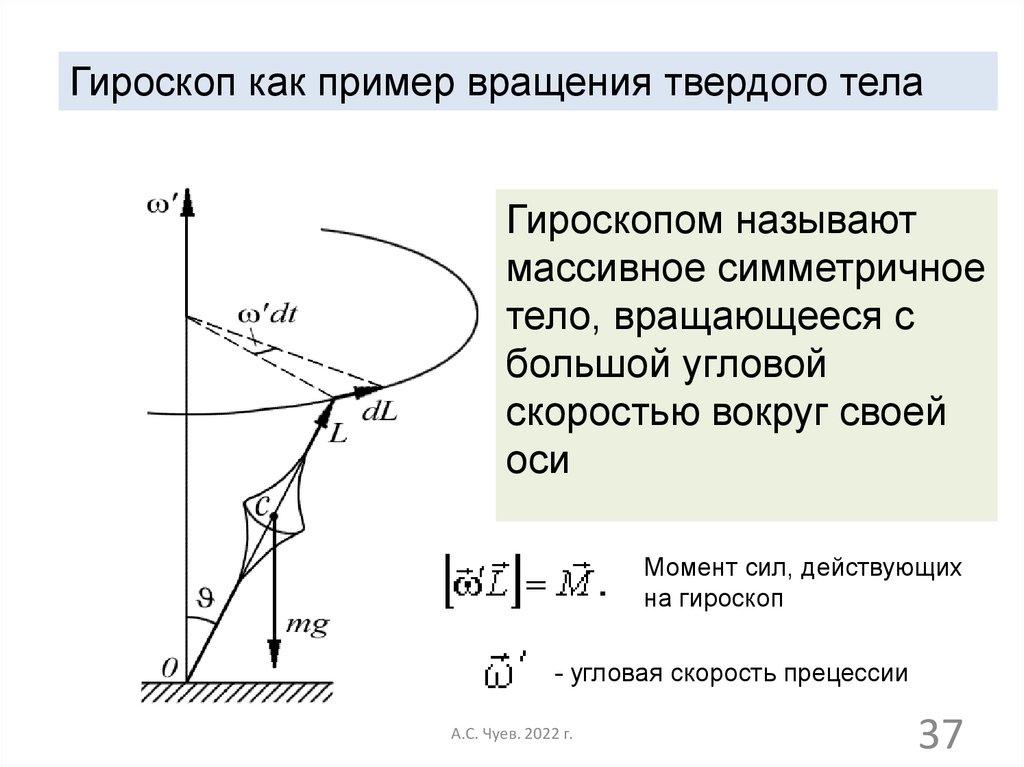
Гироскоп как пример вращения твердого телаГироскопом называют
массивное симметричное
тело, вращающееся с
большой угловой
скоростью вокруг своей
оси
Момент сил, действующих
на гироскоп
- угловая скорость прецессии
А.С. Чуев. 2022 г.
37
38.
- момент импульса от вращения вокруг собств. оси.- дополнительный момент импульса от движения
прецессии.
При условии:
L I
согласно уравнению моментов
Приращение момента импульса совпадает с
направлением момента внешней силы и
т.к.
Прецессионное движение не обладает инерцией !!!
А.С. Чуев. 2022 г.
38
39.
ФАКУравновешенный гироскоп – быстро
вращающееся тело, имеющее три степени свободы
Гироскопы используются в различных
навигационных устройствах кораблей,
самолетов, ракет (гирокомпас, гирогоризонт).
39
А.С. Чуев. 2022 г.
40.
Законы сохранения и причина ихдействия по теореме Э. Нётер
Энергии
Однородность
времени
Импульса
Однородность
пространства
Момента импульса
Изотропность
пространства
Электрического заряда Симметрия П-В к
градиентным
преобразованиям
А.С. Чуев. 2022 г.
40
41.
ФАКВИДЕОМАТЕРИАЛЫ ПО ТЕМЕ:
http://www.youtube.com/watch?v=QMl2FTqTji4
http://www.youtube.com/watch?v=nR_E-Zmqq4M
http://www.youtube.com/watch?v=LR5hkgfRPno
Эффект Джанибекова
http://www.youtube.com/watch?NR=1&v=6UYA-O6Ghas&feature=endscreen
А.С. Чуев. 2022 г.
41
42.
ФАКА.С. Чуев. 2022 г.
42
43.
А.С. Чуев. 2022 г.43
44.
ФАКhttp://www.bmstu.ru/ps/~chuev/
Файлы. Директория: Физика 1 курс 2014.
Видео по системе физических величин и закономерностей в механике
https://www.youtube.com/watch?v=nf6KPEijD2E&t=33s
Видеоблог Чуева (все видео)
https://www.youtube.com/channel/UCJzU3tDZf8j5CPWB1EZvMuA/videos?v
iew=0&sort=dd&shelf_id=1&view_as=subscriber
Видео семинара 2 по динамике вращательного движения
https://www.youtube.com/watch?v=84cr0qICSVQ
А.С. Чуев. 2022 г.
44
45.
Конец лекции 3А.С. Чуев. 2022 г.
45




























 physics
physics








